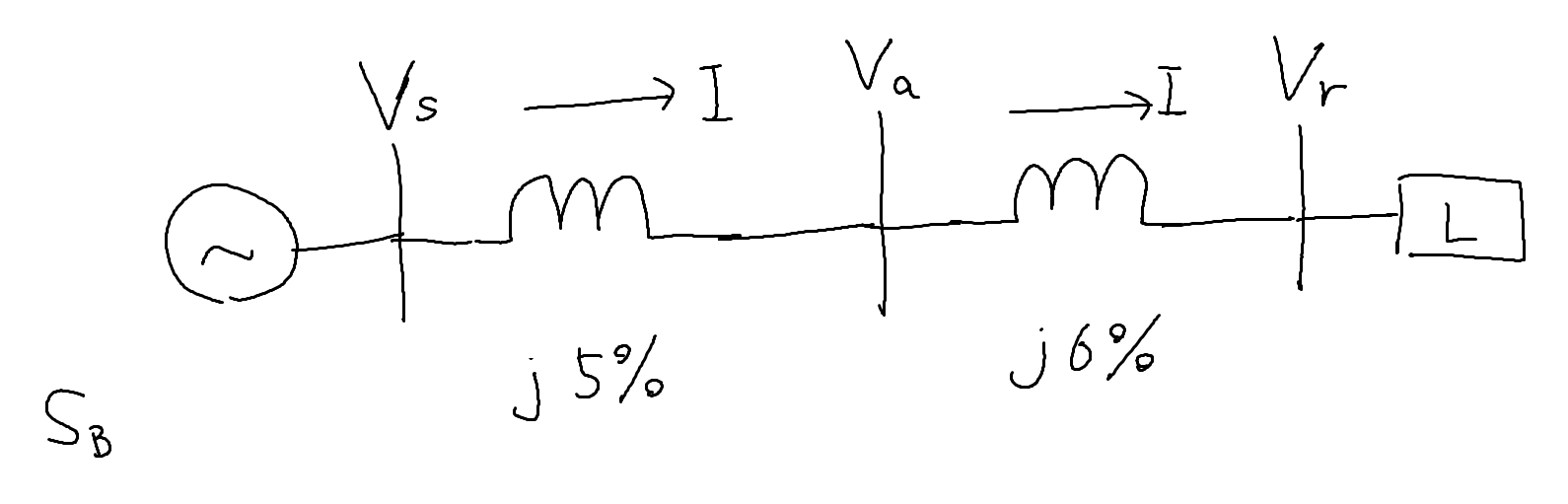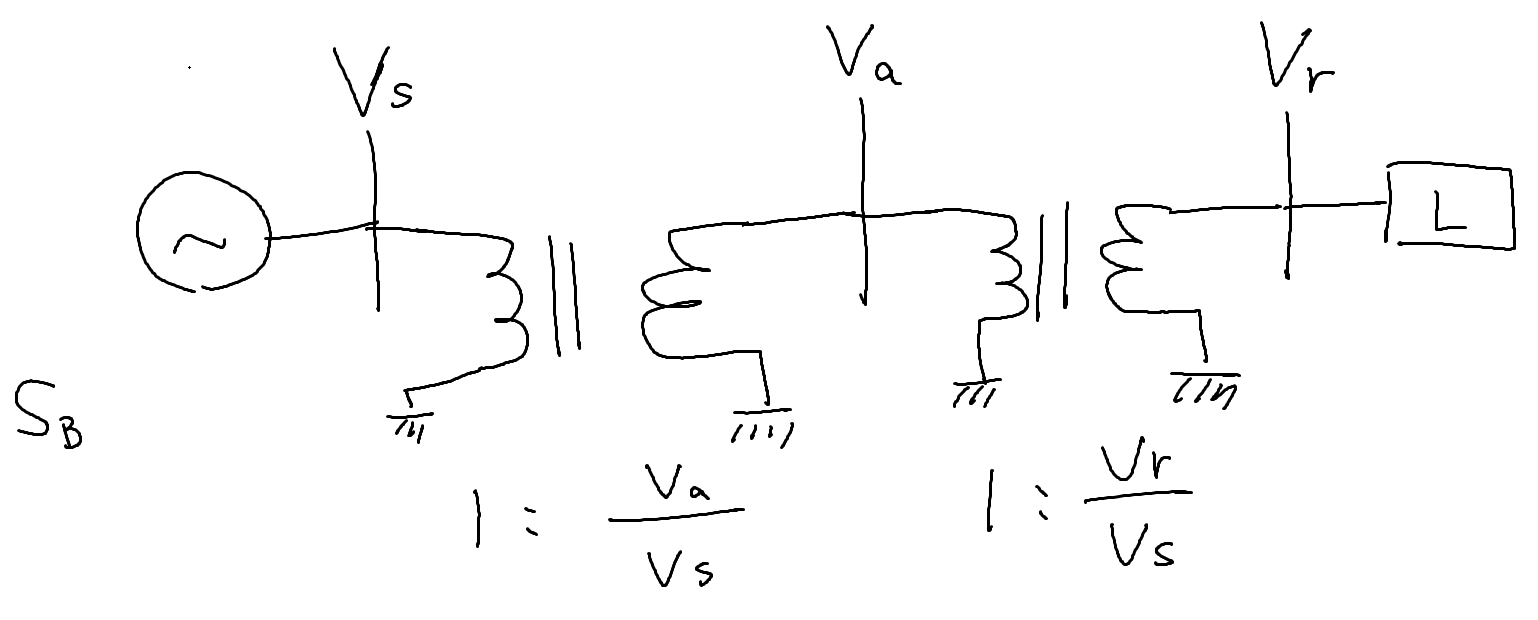単位法の足し算・引き算とは
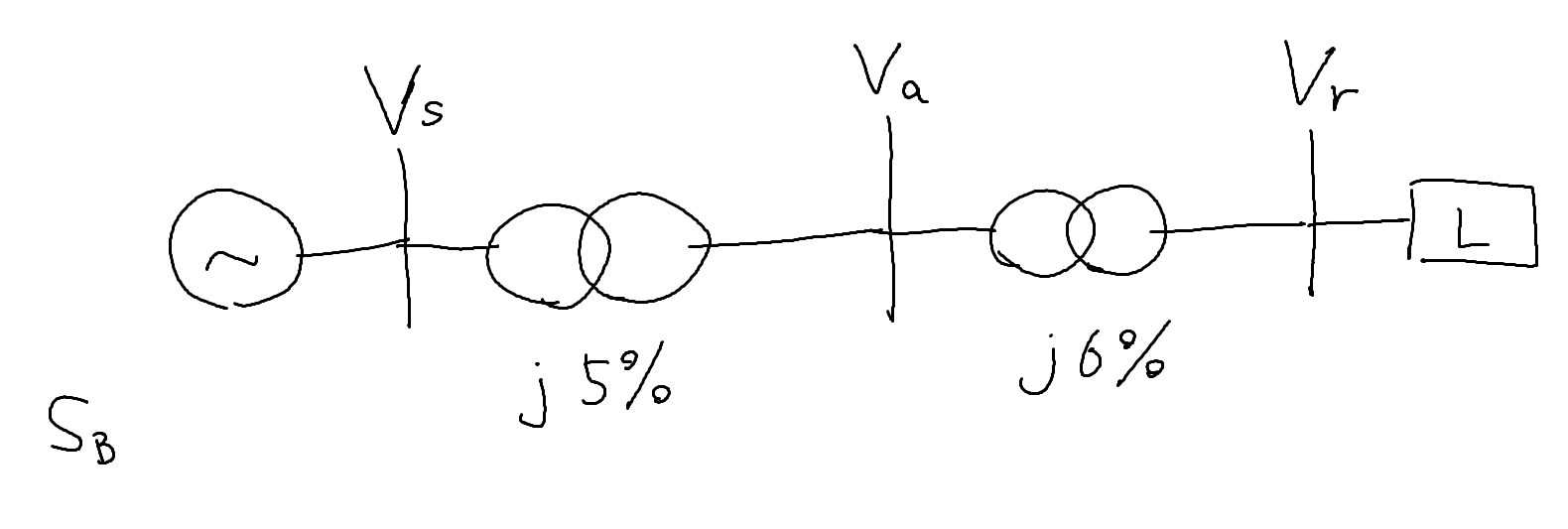
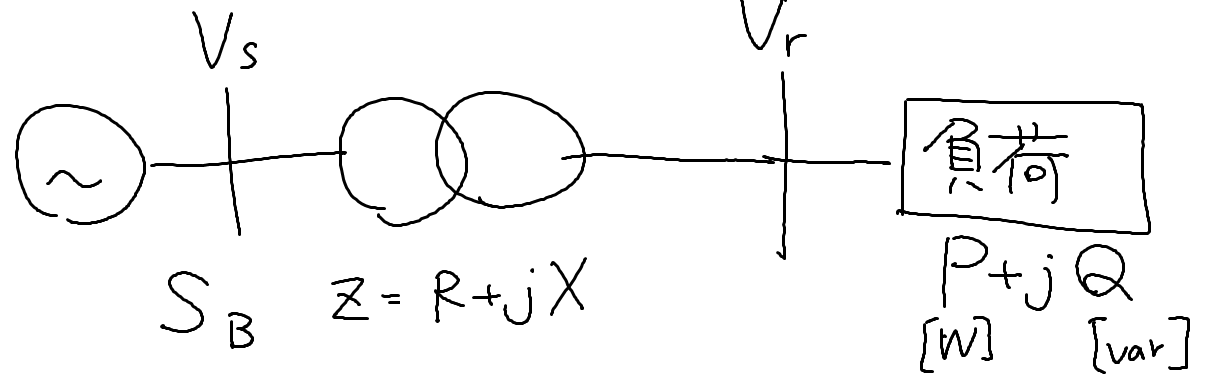
2つの変圧器を通して負荷$L$に供給する状況を考えます。
電圧$Va$を求めたい状況だとします。
間違った考え
\begin{eqnarray}
I &=& \frac{V_s - V_r}{j11 \%}\\
V_a &=& V_s - j5 \% I \\
&=& V_s - j5 \% \frac{V_s - V_r}{j11 \%} \\
&=& V_s(1-\frac{5}{11}) +V_r \frac{5}{11}\\
\end{eqnarray}
電圧差を抵抗で割り電流を出す。
電流に抵抗をかけて電圧降下を計算する。
これは誤りです。
なぜなのか
%Zを使って計算している以上、変圧器だったことを忘れていまいますが、
変圧前後の電圧で足し引きしてはいけません!
正しい計算
単位法を使えば足し算・引き算ができます。
単位法に変換したものを、pで表します。
電圧変動で変わった値をダッシュで表します。
\begin{eqnarray}
V^p_r = V'_r / V_r\\
V^p_a = V'_a / V_a\\
\end{eqnarray}
\begin{eqnarray}
\% Z &=& \frac{Z}{Z_n}\\
&=& \frac{Z S_B}{V_n^2}\\
\therefore Z &=& \% Z \frac{V_n^2}{S_B}
\end{eqnarray}
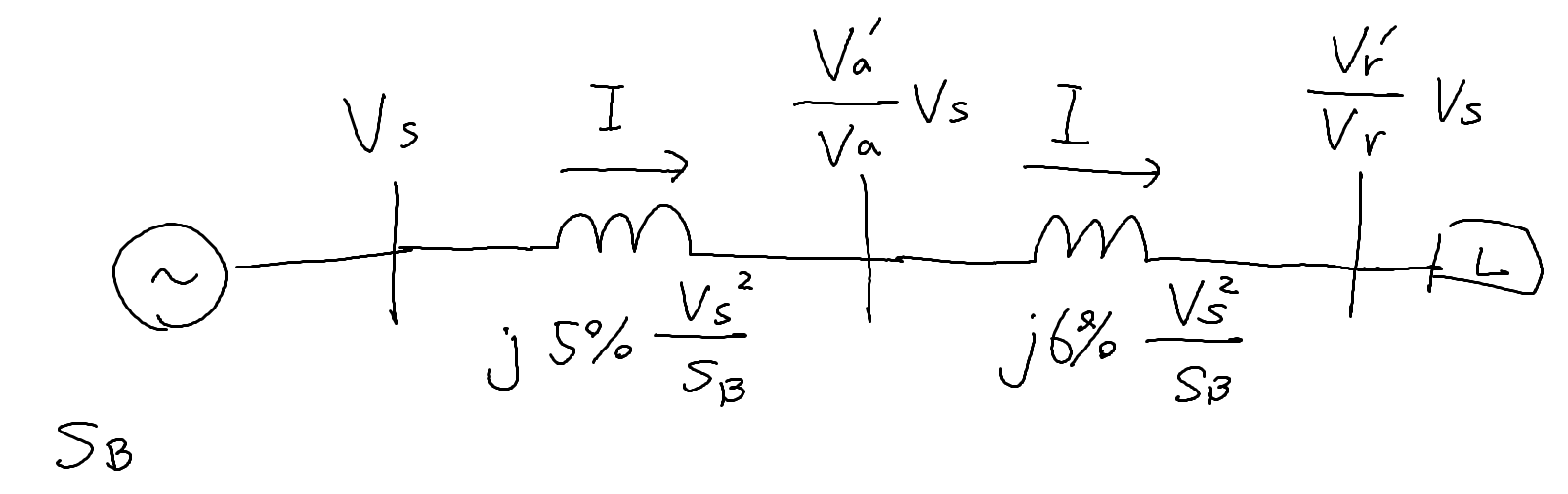
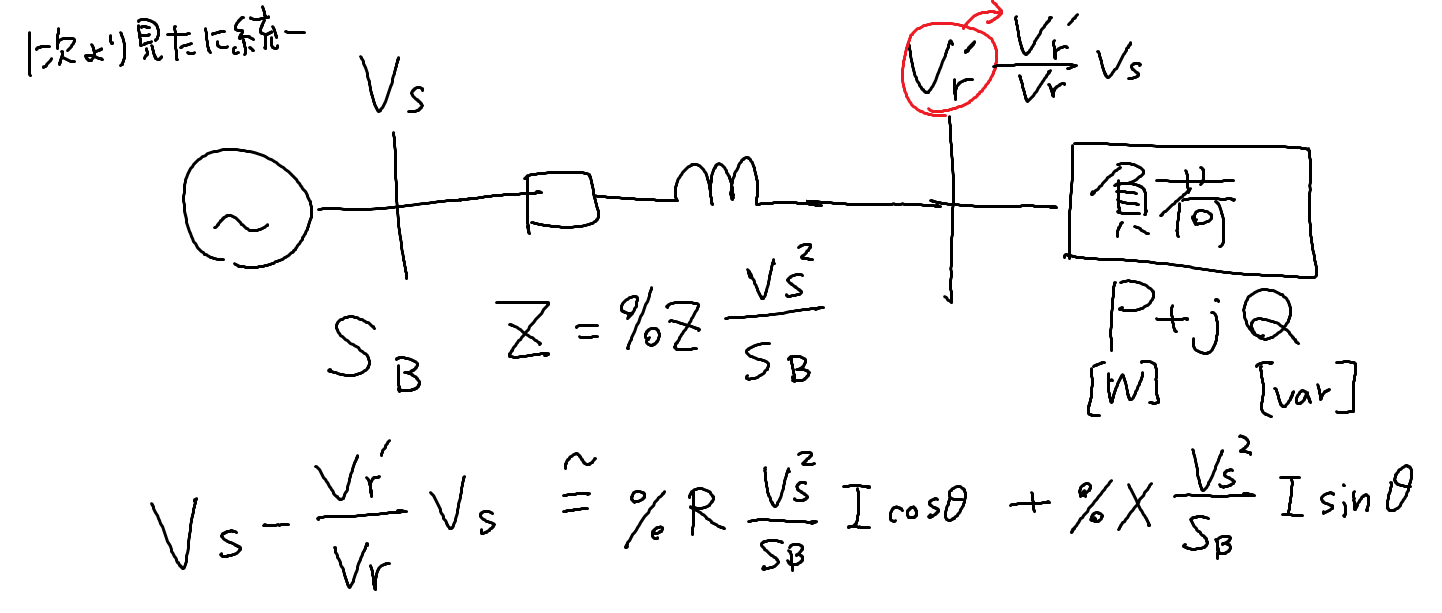
%Zを抵抗として設定して、1次側$V_s$側から見た値に全て変換してみましょう。
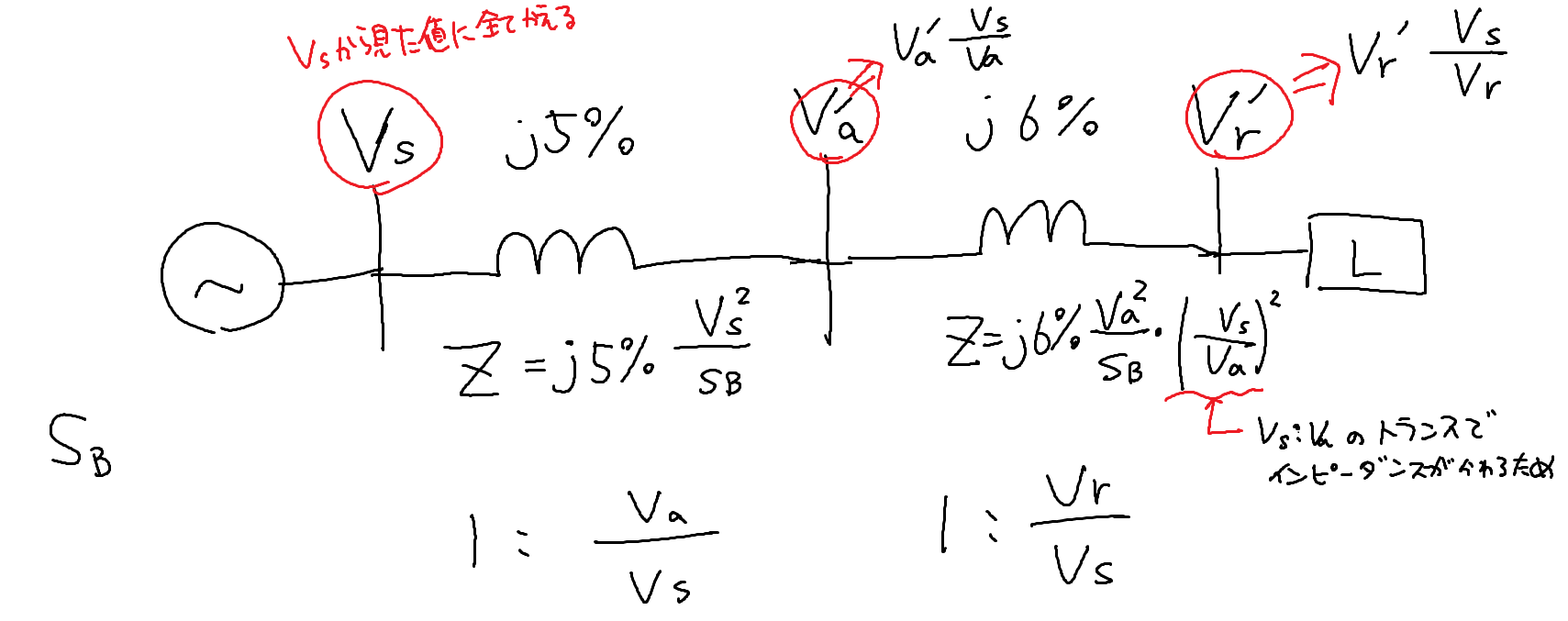
まとめると、
$V_r,V_a$が単位法の形になってきましたね。
\begin{eqnarray}
I &=& \frac{V_s - \frac{V'_r}{V_r} V_s}{j11 \% \frac{V_s^2}{S_B}}\\
&=&\frac{1 - V^p_r }{j11 \%} \frac{S_B}{V_s}\\
\frac{V'_a}{V_a} V_s &=& V_s - j5 \% \frac{V_s^2}{S_B}I \\
&=& V_s - j5 \% \frac{V_s^2}{S_B} \frac{1 - V^p_r }{j11 \%} \frac{S_B}{V_s} \\
&=& V_s - \frac{5 \%}{11 \%} (1 - V^p_r ) V_s\\
\therefore V^p_a &=& 1 - \frac{5 \%}{11 \%} (1 - V^p_r )
\end{eqnarray}
最後に出来上がった式をもう一回見てみましょう。
V^p_a = 1 - \frac{5 \%}{11 \%} (1 - V^p_r )
これは、最初にやった間違えた考え方について、単位法に書き換えた式(下)について、単位法に置き換えたと見ていいです!
\begin{eqnarray}
V_a &=& V_s - j5 \% \frac{V_s - V_r}{j11 \%}
\end{eqnarray}
見る方向に変換したりしましたが、最初から単位法で考えていれば、こんなややこしいことをしなくても、同じ結果が得られるということです。
間違った考え方は、変圧1次2次電圧で足し引きしているのが問題でしたが、単位法であれば1次2次での足し引きも問題ありません。
単位法なら、なぜ足し引きしていいのか?
実値の場合、変圧比に基づいて変換して、足し引きが必要でした。
ここで言う変換は$n^2$を掛けることでした。
単位法は基準で割ることでした。基準にも$n^2$を掛けることになるので、単位法で表した値は変圧比での変換前後で値が変わりません。
変換してから足し引きしないといけなかったですが、変換しても値が変わらないなら、
変換前で足し引きしてもいいのです!
%Zについて
例題の中でもやっていましたが、変圧器を通してで抵抗値は$Z$から$n^2 Z$に変わって見えます。
%Zの導出式は下記です。
\begin{eqnarray}
\% Z
&=& \frac{Z }{V_n^2} S_B\\
\end{eqnarray}
変圧変換で$V_n$も$n V_n$に変わります。
よって、%Zはトランス変換前後で値が変わりません。
結論
変圧器前後での電圧の足し引きをする場合は単位法で行おう!
%Zはトランスの変換から逃げるためだというのは理解していましたが、
単位法もトランスの変換から逃げるためだという点を理解していませんでした。
良い学びでした。
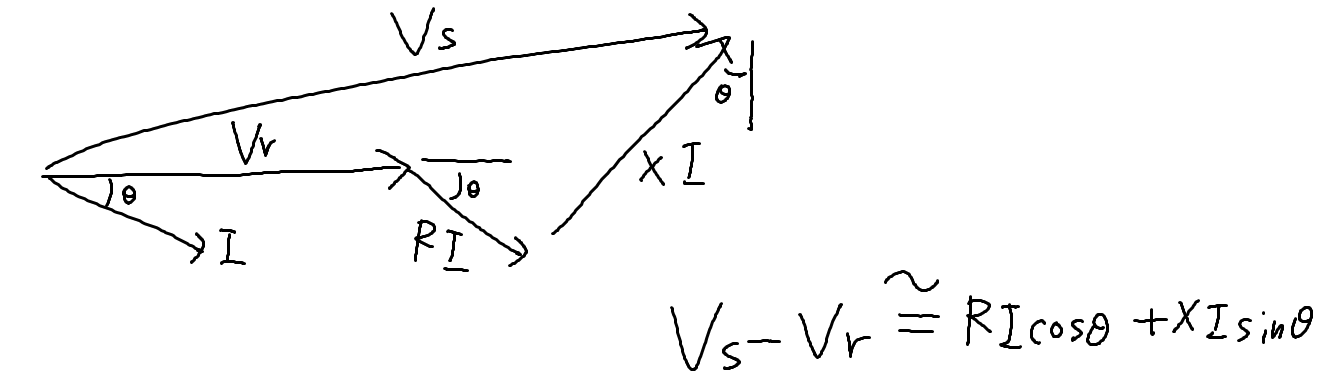
(追記)電圧降下の近似式の場合
\begin{eqnarray}
V_s - V_r = \frac{RP+XQ}{V_r}
\end{eqnarray}
変圧比を入れて考え直す
Zがどちらから見るか、最初の絵には書いてないため、おかしな状況です。
$% Z = %R + %X$であるとしましょう。変圧比を$n:1$とすれば、
1次側から見ると抵抗は$n^2R$
2次側から見ると抵抗は$\frac{1}{n^2}R$
\begin{eqnarray}
\% Z &=& \frac{Z }{V_n^2} S_B\\
Z(1次側から見た) &=& \%Z \frac{V_s^2}{S_B}\\
Z(2次側から見た) &=& \%Z \frac{V_r^2}{S_B}\\
\end{eqnarray}
負荷に流れる電流$I$は2次側の値です。1次側に変換する必要があります。
$\frac{V_r}{V_s} I $が1次側にから見て流れている電流です。
式を変形していきます。
\begin{eqnarray}
V_s - V^p_r V_s &=& \% R \frac{V_s^2}{S_B} \frac{V_r}{V_s} I cos \theta + \%X \frac{V_s^2}{S_B} \frac{V_r}{V_s} I sin \theta\\
&=& \% R \frac{V_s^2}{S_B} \frac{P}{V_s} + \%X \frac{V_s^2}{S_B} \frac{Q}{V_s}\\
&=& (\% R \frac{P}{S_B} + \%X \frac{Q}{S_B} ) V_s\\
\therefore 1 - V^p_r &=& \% R \frac{P}{S_B} + \%X \frac{Q}{S_B} \\
\end{eqnarray}
つまり、単位法を使う場合は%Zで同様の計算ができます。
負荷を基準容量で単位法にしている点だけ理解すれば完全に同じです。
\begin{eqnarray}
1 - V^p_r &=& \% R \% P + \%X \% Q\\
\end{eqnarray}
とも書けます。
正確には異なる
上の式、正確には間違いがあります。どこでしょう・・・
答えは、$P=V_r I cos\theta$としている点です。正確には$V'_r I cos\theta$とする必要があります。
\begin{eqnarray}
V_s - V^p_r V_s &=& \% R \frac{V_s^2}{S_B} \frac{V_r}{V_s} I cos \theta + \%X \frac{V_s^2}{S_B} \frac{V_r}{V_s} I sin \theta\\
&=& \% R \frac{V_s^2}{S_B} \frac{P}{V_s} \frac{V_r}{V'_r} + \%X \frac{V_s^2}{S_B} \frac{Q}{V_s} \frac{V_r}{V'_r} \\
&=& (\% R \frac{P}{S_B} + \%X \frac{Q}{S_B} ) V_s \frac{1}{V^p_r} \\
\therefore 1 - V^p_r &=& \frac{\% R \frac{P}{S_B} + \%X \frac{Q}{S_B} }{V^p_r}\\
\end{eqnarray}
いつもの式(下)とほぼ同じになりました。単位法になっても、分母の受け手側の電圧で割ることは必要なようです。
\begin{eqnarray}
V_s - V_r = \frac{RP+XQ}{V_r}
\end{eqnarray}
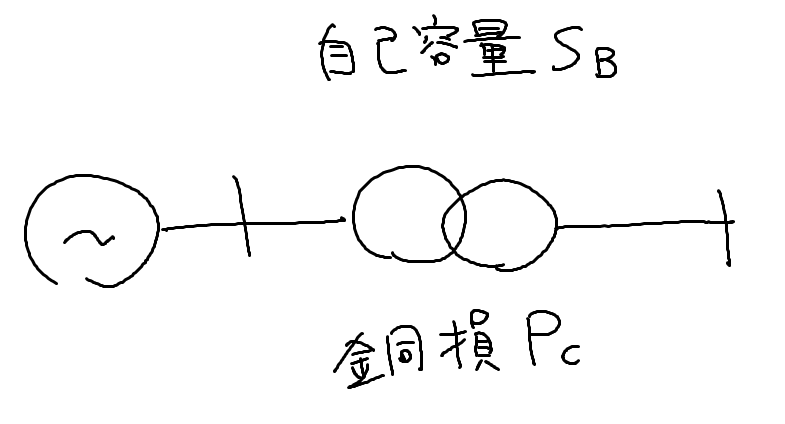
(追記)銅損を%Rに変換するときのミス
\begin{eqnarray}
P_c &=& 3RI_n^2\\
S_B &=& \frac{V_n^2}{Z_n}\\
\%R &=& \frac{R}{Z_n} = \frac{P_c}{3 I_n^2} \frac{S_B}{V_n^2} = \frac{P_c}{S_B}
\end{eqnarray}
誤答
\begin{eqnarray}
P_c &=& 3RI_n^2 = 3 \frac{E_n^2}{R} =\frac{V_n^2}{R} \therefore R = \frac{V_n^2}{P_c}\\
S_B &=& \frac{V_n^2}{Z_n} \therefore Z_n = \frac{V_n^2}{S_B}\\
\%R &=& \frac{R}{Z_n} = \frac{V_n^2}{P_c} \frac{S_B}{V_n^2} = \frac{S_B}{P_c}\\
\end{eqnarray}
それっぽい式になりましたが、最初とは分子分母が逆になりました。
どこで間違ったのでしょうか。
答えは、最初の1行目の$I_n=E_n/R$としたところです。$I_n=E_n/Z_n$にしないといけません。
そこでの間違いを引きづって失敗してしまっています。
無効電力の計算
話が逸れちゃいますが、電力は以下の式で計算できました。
\begin{eqnarray}
P=V \bar{I}
\end{eqnarray}
コイルでは電流は遅れ、共役を取って掛け算するので、無効電力は正になります。
式を変形すると、
\begin{eqnarray}
P&=&V \bar{(\frac{V}{Z})}\\
&=& \frac{V^2}{ \bar{Z}}
\end{eqnarray}
\begin{eqnarray}
P&=& IZ \bar{I}\\
&=& I^2 Z
\end{eqnarray}
何が言いたいかというと、$I^2Z$を使う場合は共役複素数を使う必要がなく、
インピーダンスが正(コイル)なら、無効電力も正となるということです。
しかし、$V^2/Z$を使う場合は、共役複素数を使う必要があります。
インピーダンスが正(コイル)なら、共役によって負になり、わり算によって正に戻ります。
$V^2/R$は共役を取る必要があることを忘れないようにしましょう。