はじめに
これまで機械学習・統計を学んでいました。その中でも強化学習についてあまりきちんと勉強していていなかったため、実装を交えて理解を深めました。
参考資料としては下記です。
強化学習概要
強化学習(Reinforcement Learning, RL)とは、システム自身が試行錯誤しながら最適なシステム制御を実現する、機械学習手法の一つです。
Alpha Goあたりが有名ですね。
分類上は、教師あり/なし学習とも異なると位置づけられています。感覚的には教師なし学習なのですが、違うようです。
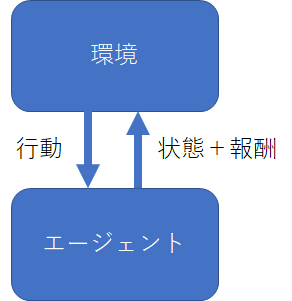
下記図が模式図となります。ある環境下で、目的とする報酬(スコア)を最大化するためにとる行動の最適化をモデルとして学習させていきます。
この行動が
- ブロック崩し→左右移動
- 囲碁→石を打つ位置
- マリオ(2D)→左右上下移動
等学習させたいゲームごとに異なってきます。
1990年代に研究自体は活発に行われていたものの、「状態」の表現方法やその「状態」に基づいて「行動」に結びつける方法を表現することが難しく、2000年代は研究の勢いが衰えていたようです。
深層強化学習
この課題に対して、2013年に**DeepMind社が畳み込みニューラルネットワーク(CNN)を組み合わせた強化学習によるブロック崩し**を公開し、大きな反響を集めました。
ここで用いられる強化学習の手法に**Q学習(Q Learning)**とDeep Learningを組み合わせていることから、DQN(Deep Q-Network)と呼ばれています。
**ただ、今回の実装では単純なQ学習で行います。**次回以降、DQNで実装編を作れればと思います。。
Cart Poleを実装する
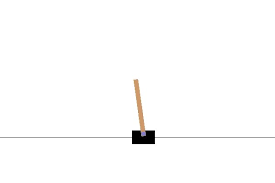
今回は、強化学習のMNIST的な存在であるCart Poleを扱います。これは、1次元的な動き(左右)をする滑車に棒が載っています。この棒が倒れないように滑車の動きを学習させていく内容です。
非常にシンプルです。状態パラメータは下記4つになります。
- カートの位置 (-2.4~+2.4)
- カートの速度(-inf~+inf):無限大
- ポールの角度(-41.8°~+41.8°):絶対値が40以上で倒れる
- ポールの速度(-inf~+inf)
一方で行動パラメータは下記2つです。
- 左にカートが動く(0)
- 右にカートが動く(1)
報酬はボールが倒れない限り1得られます。また、1エピソードを1つのゲームが終了するまでの期間とします。そして、
- 100エピソード連続で195以上の報酬が得られれば成功
- エピソードのタイムステップの長さは最大で200
とします。
単純に動かした場合
何も気にせず単純にnp.random.choice([0,1])として、0か1をランダムで動かします。するとどうなるでしょうか。
import gym
import numpy as np
env = gym.make('CartPole-v0')
goal_average_steps = 195
max_number_of_steps = 200
num_consecutive_iterations = 100
num_episodes = 200
last_time_steps = np.zeros(num_consecutive_iterations)
for episode in range(num_episodes):
# 環境の初期化
observation = env.reset()
episode_reward = 0
for t in range(max_number_of_steps):
# CartPoleの描画
env.render()
if env.viewer == None:
env.render()
# ランダムで行動の選択
action = np.random.choice([0, 1])
# 行動の実行とフィードバックの取得
observation, reward, done, info = env.step(action)
episode_reward += reward
if done:
print('%d Episode finished after %d time steps / mean %f' % (episode, t + 1,
last_time_steps.mean()))
last_time_steps = np.hstack((last_time_steps[1:], [episode_reward]))
break
if (last_time_steps.mean() >= goal_average_steps): # 直近の100エピソードが195以上であれば成功
print('Episode %d train agent successfuly!' % episode)
break
すると以下のように表示されます。
185 Episode finished after 21 time steps / mean 21.350000
186 Episode finished after 23 time steps / mean 21.390000
187 Episode finished after 22 time steps / mean 21.510000
188 Episode finished after 39 time steps / mean 21.420000
189 Episode finished after 13 time steps / mean 21.320000
190 Episode finished after 9 time steps / mean 21.160000
191 Episode finished after 26 time steps / mean 20.980000
192 Episode finished after 17 time steps / mean 21.100000
193 Episode finished after 94 time steps / mean 21.120000
194 Episode finished after 15 time steps / mean 21.870000
195 Episode finished after 26 time steps / mean 21.880000
196 Episode finished after 13 time steps / mean 21.970000
197 Episode finished after 13 time steps / mean 21.940000
198 Episode finished after 31 time steps / mean 21.760000
199 Episode finished after 23 time steps / mean 21.950000
凡そ数十回のタイムステップで途切れてしまうことが分かります。学習をしていないので数が増えないことは理解できます。
Q Learningで学習させる
さて、Q Learningで学習させましょう。
ここでポイントとなる考え方は、ある場面において次に取るべき行動を選択する指標を設けることです。この値をQ値と呼びます。プログラム上は、Q_tableと定義して下記のような行列になります。
今回であれば、下記のカート及びポールの状態をそれぞれ4分割した4つの状態があるため、$4^4=256$にさらに左右の行動$2$で$256×2$の行列となります。
- カートの位置 (-2.4~+2.4)
- カートの速度(-inf~+inf):無限大
- ポールの角度(-41.8°~+41.8°):絶対値が40以上で倒れる
- ポールの速度(-inf~+inf)
このQ値を行動ごとに改善させていきます。Q値は大きいほうが選択されやすいため、このQ値を報酬が大きくなるような形で増やすことで行動が改善されます。
さて、このQ値の更新は下記式になります。
Q(s, a) = (1 - \alpha)Q(s, a) + \alpha(R(s, a) + \gamma max_{a'} E[Q(s', a')])
ここで
- $Q(s,a)$状態s,行動aをとる値
- $α$ 学習率
- $γ$ 割引率
- $max_{a'} E[Q(s', a')]$次の時刻において選択できる行動のQ値でMax値
となります。
これを実装すると下記のようになります。
def get_action(state, action, observation, reward):
next_state = digitize_state(observation)
next_action = np.argmax(q_table[next_state])
# Qテーブルの更新
alpha = 0.2
gamma = 0.99
q_table[state, action] = (1 - alpha) * q_table[state, action] +\
alpha * (reward + gamma * q_table[next_state, next_action])
return next_action, next_state
for episode in range(num_episodes):
# 環境の初期化
observation = env.reset()
state = digitize_state(observation)
action = np.argmax(q_table[state])
episode_reward = 0
for t in range(max_number_of_steps):
# CartPoleの描画
#env.render()
# 行動の実行とフィードバックの取得
observation, reward, done, info = env.step(action)
# 行動の選択
action, state = get_action(state, action, observation, reward)
episode_reward += reward
これで実際に100試行程度で学習が収束して、成功します。
終わり
強化学習の概要とCart Poleにて遊びました。DQNにも挑戦したいと思います。
プログラム全文は下記です。
https://github.com/Fumio-eisan/RL20200527