住宅価格を予測する（LinearRegressionによる回帰(kaggle)）ver1.0

#１　はじめに

　今回は、Sale Price(住宅価格）予測問題について解いていきます。最初は極々簡単な一次回帰式から予測を行いたいと思います。本来は多数ある特徴量を処理、最適化していくことが醍醐味なのですが、まずは簡単に予測するところから始めたいと思います。

参考ＵＲＬ
https://www.kaggle.com/katotaka/kaggle-prediction-house-prices

使用したバージョンはこちらです。

Python　3.7.6
numpy　1.18.1
pandas　1.0.1
matplotlib　3.1.3
scikit-learn　0.22.1

#２　プログラムについて

#ライブラリ等

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
import seaborn as sns

# Jupyter Notebookの中でインライン表示する場合の設定（これが無いと別ウィンドウでグラフが開く）
%matplotlib inline 

　csvの読み込みとしてpandas、数列の処理としてnumpy、グラフ描画にmatplotlibとseaborn、そして回帰を行うためにsklern.linear_modelをインポートしました。

#訓練データの読み込み

df = pd.read_csv("train.csv")
df

　特徴量が多いために一度にすべてを表示することができておりませんが、多くの住宅条件（面積、道に面しているか、プールがあるか）等が記載されています。これら条件が住宅価格(Sale Price）に影響しているかを評価して、予測するものです。

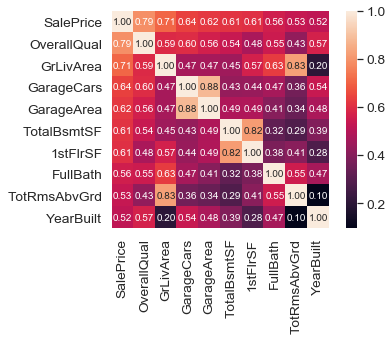
#相関係数の高い特徴量の見極め

corrmat = df.corr()
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

　住宅価格に対して相関係数が高い特徴量を見出したいと思います。seabornのheatmapによって見てみましょう。SalePriceと相関係数高い特徴量はOverallQual（全体の品質）であることが分かります。品質が高ければ値段も高くなる、ということは感覚的にも理解しやすいものですね。
　

　

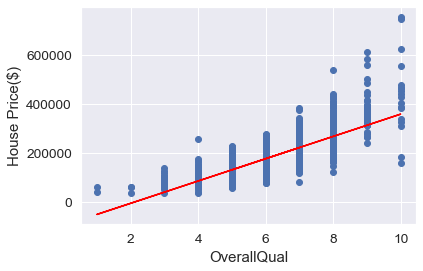
#回帰分析と散布図表示

X = df[["OverallQual"]].values
y = df["SalePrice"].values
slr = LinearRegression()
slr.fit(X,y)

#散布図作成
plt.scatter(X,y)
plt.xlabel('OverallQual')
plt.ylabel('House Price($)')

#近似曲線の表示
plt.plot(X, slr.predict(X), color='red')

#グラフ表示
plt.show()

　OverallQualとSalePriceの関係をグラフに致しました。概ねの傾向は合っています。しかし、OverallQualが低いところでは実際より低く見積もられいます。また、OverallQualが高いところではバラツキが大きいことが分かります。これらは他の特徴量によりさらに精緻に予測できると思いますが、今回はこのまま予測します。

#予測

#テストデータ読み込み
df_test = pd.read_csv('test.csv')

#テストデータのOverallQualの値をX_testへセット
X_test = df_test[["OverallQual"]].values

y_test_pred = slr.predict(X_test)
df_test[["Id", "SalePrice"]].to_csv("submission.csv", index = False)

kaggleへ送付した際のSCOREは0.84342でした(4563位4720チーム中）。
次の記事からは詳細に解析して良いスコアにしていきたいと思います。