Affairs dataset(不倫データセット)を題材にしてPandasの使い方, 多重共線性を丁寧に理解しようとした

#はじめに
　　前回、ロジスティック回帰を理論から学んだことをまとめました。

二値分類可能な判別器を自作のロジスティック回帰により作成することで、理解を深めようとした
https://qiita.com/Fumio-eisan/items/e2c625c4d28d74cf02f3

　今回は、実際のデータセットを用いてモデル推定を行いました。いわゆるデータ前処理の基本的な処理（ダミー変数化、列の削除、結合）やデータ解釈及び、多変量解析で問題になる多重共線性についてまとめました。実装的な内容が多いです。

概要は下記です。

• 今回のデータセット
• ヒストグラムで複数グラフを一つに表示してデータを解釈
• データの前処理
• 多重共線性について
• ロジスティック回帰で予測する

使用したバージョンは下記です。

• numpy 1.16.5
• pandas 0.25.1
• seaborn 0.9.0
• scikit-learn 0.21.3

##今回のデータセット

　今回は、1974年に行われた結婚女性に対して実施した不倫有無の調査結果データセットを用いました。

affair.ipynb

df = sm.datasets.fair.load_pandas().data
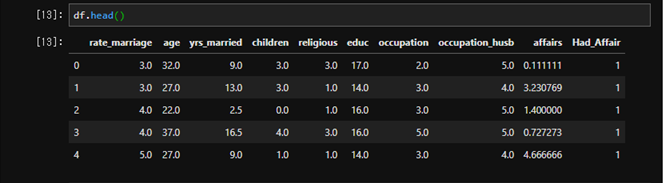
df.head()

データを眺めると結婚してからの期間、年齢、子供の有無などが説明変数として記載されていることが分かります。そして、最後にaffairs列に数値が入っています。0が不倫をしていない、1以上が不倫をしている（していた）ことを示しています。

##ヒストグラムで複数グラフを一つに表示してデータを解釈

不倫有無による差を評価します。まずは、現状のデータだとaffairsの数字がバラバラなので、不倫している（1以上）、不倫していない（0）で分けます。

affair.ipynb

def affair_check(x):
    if x!=0:
        return 1
    else:
        return 0

df['Had_Affair']=df['affairs'].apply(affair_check)

データを解釈して、予測モデルにより強い関係がありそうなパラメータを探します。そのためには、不倫あり（1）、なし（0）で分類してそれぞれ変数でヒストグラム化します。
axes(軸）を戻り値として、それぞれ表したいグラフで引数で与えます。

affair.ipynb

fig, axes = plt.subplots(nrows=3, ncols=3,figsize=(10,8))

sns.countplot(df['age'], hue=df['Had_Affair'],ax=axes[0,0])
sns.countplot(df['yrs_married'], hue=df['Had_Affair'],ax=axes[0,1])
sns.countplot(df['children'], hue=df['Had_Affair'],ax=axes[0,2])
sns.countplot(df['rate_marriage'], hue=df['Had_Affair'],ax=axes[1,0])
sns.countplot(df['religious'], hue=df['Had_Affair'],ax=axes[1,1])
sns.countplot(df['educ'], hue=df['Had_Affair'],ax=axes[1,2])
sns.countplot(df['occupation'], hue=df['Had_Affair'],ax=axes[2,0])
sns.countplot(df['occupation_husb'], hue=df['Had_Affair'],ax=axes[2,1])

さて、一度に表示できたため、これでデータの解釈をすることができます。基本的に、不倫しているグループとしていないグループでピークが異なるところにあるパラメータに着目するべきだと思います。

• 不倫していない人は22歳近辺にピークがいますが、不倫している人は27歳近辺にピークがある
• 不倫している人は子供が２人いる場合が最も多い。一方、不倫していない人は子供がいない場合が最も多い。
• 貧富（rate_marriage）については、不倫していない人はvery good（５）が最も多い一方、不倫している人はgood（４）が最も多い。

##データの前処理

###ダミー変数の導入

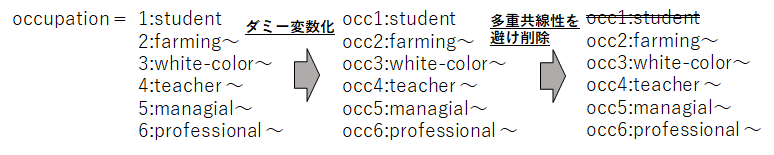
さて、予測モデルを作るにあたり前処理を行います。今回の不倫データセットにおいて、カテゴリー型の変数になっているものは、職業(Occupation）と夫の職業（Husband's Occupation）です。これらに対して、ダミー変数を導入して0/1表現で分類します。

このようなイメージです。実装は下記になります。

affair.ipynb

occ_dummies = pd.get_dummies(df['occupation'])
hus_occ_dummies = pd.get_dummies(df['occupation_husb'])
occ_dummies.columns = ['occ1','occ2','occ3','occ4','occ5','occ6']
hus_occ_dummies.columns = ['hocc1','hocc2','hocc3','hocc4','hocc5','hocc6']
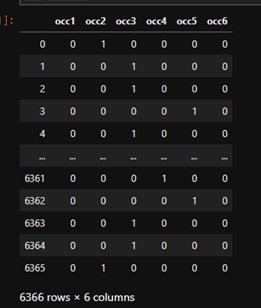
occ_dummies

無事に分けることができました。

###データの削除と接続

　次に、必要のない列を削除することと、必要な列を接続したいと思います。
occupationやHad_Affairの列を削除します。

affair.ipynb

X = df.drop(['occupation','occupation_husb','Had_Affair'],axis=1)

　　
　そして、ダミー変数化したものをまとめます。

affair.ipynb

dummies = pd.concat([occ_dummies,hus_occ_dummies],axis=1)

　最後に、ダミー変数化したものと元のデータを結合します。

affair.ipynb

XX = pd.concat([X,dummies],axis= 1)

##多重共線性について

続いて、多重共線性について考えます。説明変数の種類が増えてくると現れる問題です。この説明変数の中で、互いに相関係数が強い現象を多重共線性と呼びます。多重共線性が多いと回帰式の精度が極端に悪くなる等、解析結果が不安定な状態になる場合があります。

　例えば、住宅価格を予測するモデルにおいて、「部屋の数」と「部屋の面積」は強い相関があることが予想されます。このような場合、片方の変数を除外することで多重共線性を避けることができます。

　今回では、ダミー変数化したoccupationの中から、occ1,hocc1＝学生を除外してモデルを作ってみたいと思います。

affair.ipynb

XX = XX.drop('occ1',axis=1)
XX = XX.drop('hocc1',axis=1)

上図のような関係になりますね。

##ロジスティック回帰で予測する

そして、モデルを予測します。今回はscikit learnのロジスティック回帰で簡単に予測していきたいと思います。
　訓練データだけで最初モデルを学習させます。そして、テストデータで予測します。

affair.ipynb

X_train, X_test, Y_train, Y_test = train_test_split(XX, Y)
model2 = LogisticRegression()
model2.fit(X_train, Y_train)
class_predict = model2.predict(X_test)
print(metrics.accuracy_score(Y_test,class_predict))

0.707286432160804

７０％くらいの正解率であることが分かりました。それでは、先ほどの多重共線性を避けて消したデータをそのまま消さなかった場合（＝要はデータそのまま）ではどうなるでしょうか。

affair.ipynb

X2_train, X2_test, Y2_train, Y2_test = train_test_split(X2, Y)
model3 = LogisticRegression()
model3.fit(X2_train, Y2_train)
class_predict2 = model3.predict(X2_test)
print(metrics.accuracy_score(Y2_test,class_predict2))

0.9748743718592965

９７％と正答率が高くなりました。今回のケースでは多重共線性を起こさないため、データはそのままの方がよかったということが分かります。

　つまり、多重共線性を考慮しなければならないかどうかは、一旦全部のデータを入れて計算した場合と削除した場合で検討しなければわからないようです。経験的なところがモノをいう手続きであることが分かりました。

#終わりに
　pandasやmatplotlibを用いてデータの解釈及び、多重共線性を考慮した前処理を行いました。チュートリアル的なデータセットであるため、すんなり進んだように見えますが、グラフ描写や結合等、pandasの取り扱いがまだまだと思いました。
　
　また、ロジスティック回帰自体の実装は非常に簡便であるため、中で何が起きているかまったく知らなくても計算できることは、非常に便利でした。

プログラム全文はこちらにあります。
https://github.com/Fumio-eisan/affairs_20200412