はじめに
今回はロジスティク回帰について、scikit learnなどのフレームワークを用いずに実装することで理解を深めた内容をまとめます。
概要は下記です。
- 回帰分析とロジスティク回帰
- ロジスティック回帰を実装して理解に努める
回帰分析とロジスティク回帰
ロジスティック回帰を説明する前に、回帰分析についてまとめます。
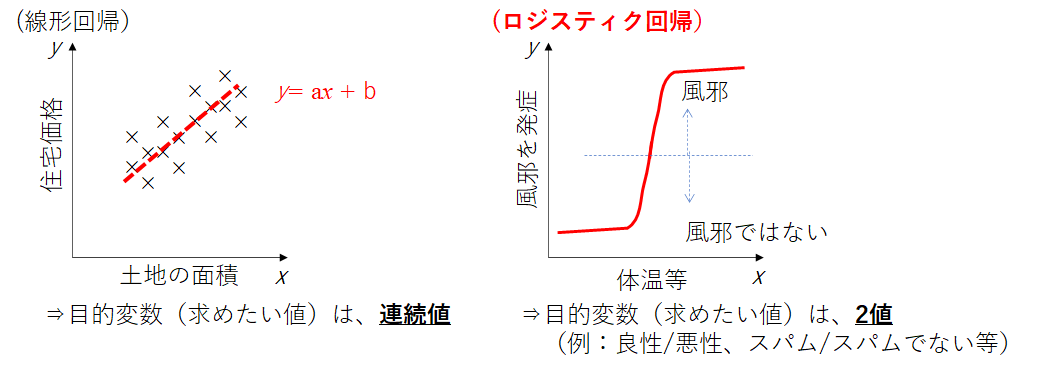
回帰とは、目的変数$y$について説明変数$x$を使った式で表すことをいいます。そしてこの$y$は連続の値を取ります。$x$が一次元なら単回帰、二次元以上なら重回帰と呼びます。
例としては、
- 土地面積(説明変数)の広さから土地価格(目的変数)を予測
- 広告宣伝費(説明変数)から店の来店者数(目的変数)を予測
- 身長(説明変数)のから体重(目的変数)を予測
等が挙げられます。土地価格や来店者数などは連続した値であることが分かります。
一方、ロジスティック回帰とは、説明変数からあるクラスに属する確率(例えば、メールがスパムかどうか)を推算する方法のことを呼びます。
線形回帰と同じように、説明変数を元に線形計算を実施します。しかし、その計算結果をそのまま出力するのではなく、結果のロジスティック(Logistic)を返します。
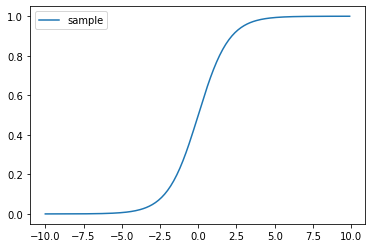
ロジスティックとは、0から1までの値を出力することを指します。この時、ロジスティック回帰に用いられる関数をシグモイド関数と呼びます。
f(x) = \frac{1}{1+e^{-x}} \\
x = β_0×α_0 +β_1
$β_0×α_0 +β_1$が線形回帰で用いる回帰式です($β_0,β_1$が定数、$α_0$が変数としています)。今回は一例で$\alpha$の一次式と置いています。$f(x)$が0から1を返します。
ロジスティック回帰を実装して理解に努める
さて、今回はロジスティック回帰をsckit learnなどのフレームワークを用いずに自作しながら進めたいと思います。
- ランダムな点(二次元)を百個生成
- ある一次元の直線(今回はf(x,y)=2x+3y-1)を基準に、上記百個の点をf(x,y)>0か<0で分類
- 適当な識別器$w$(3次元ベクトル)を作成。基底関数$φ=(x,y,1)$との結合$w・φ$をシグモイド関数で0~1出力
- 確率的降下法で3.のパラメータを更新して、f(x,y)を区別できるパラメータにする
- 判別器がf(x,y)を識別可能となる
ランダムな点(二次元)を百個生成
まずは、x,yの点をnp.random.randn()メソッドにて二次元平面状にランダムな点を100個生成します。
N = 100# データ点の個数
np.random.seed(0)# データ点のために乱数列を固定
X = np.random.randn(N, 2)# ランダムな N×2 行列を生成 = 2次元空間上のランダムな点 N 個
ある一次元の直線(今回はf(x,y)=2x+3y-1)を基準に、上記百個の点をf(x,y)>0か<0で分類
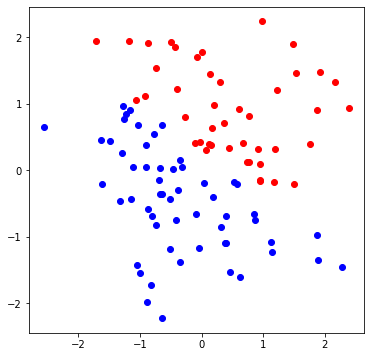
次にある一次元の直線(今回はf(x,y)=2x+3y-1)を引いて、ランダムな百点をf(x,y)>0 か<0で分類します。
def f(x, y):
return 2 * x + 3 * y - 1 # 真の分離平面 2x + 3y = 1
T = np.array([ 1 if f(x, y) > 0 else 0 for x, y in X])
plt.figure(figsize=(6, 6))
plt.plot(X[T==1,0], X[T==1,1], 'o', color='red')
plt.plot(X[T==0,0], X[T==0,1], 'o', color='blue')
plt.show()
分類したくなる直線が見えました。
適当な識別器$w$(三次元ベクトル)を作成。基底関数$φ=(x,y,1)$との結合$w・φ$をシグモイド関数で0~1出力
次に、識別器として三次元ベクトル$w$を生成します。そして基底関数として$φ=(x,y,1)$を定義します。この内積(それぞれの成分どおしを掛けて足したもの)を求めます。
線形回帰問題の場合は、この内積値で予想をします。しかし、ロジスティック回帰ではさらにこの内積値をシグモイド関数へ代入することで得られる0~1の値から予測することがポイントです。
実際に実装すると下記になります。
np.random.seed() # 乱数を初期化
w = np.random.randn(3) # パラメータをランダムに初期化
def phi(x, y):# 基底関数
return np.array([x, y, 1])
seq = np.arange(-3, 3, 0.1)
xlist, ylist = np.meshgrid(seq, seq)
zlist = [sigmoid(np.inner(w, phi(x, y))) for x, y in zip(xlist, ylist)] #パラメータと基底関数を内積し、シグモイド関数へ代入
plt.imshow(zlist, extent=[-3,3,-3,3], origin='lower', cmap='bwr')
plt.show()
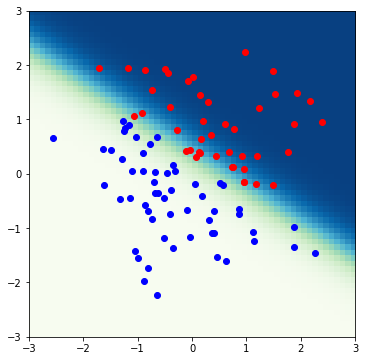
その識別器によって得られる分布が上の図になります。凡そ0.5以上(=[1])が赤、0.5以下(=[0])が青色を示す領域(教師データとなる正解の領域)になります。この分かれている領域を先ほどのf(x,y)で判別している領域に合わせれば成功です。
確率的勾配降下法で3.のパラメータを更新して、f(x,y)を区別できるパラメータにする
次に、確率的勾配降下法によって識別器のパラメータを更新します。確率的勾配降下法については、ニューラルネットワークでの説明例になりますがこちらでまとめています。
ニューラルネットワークにおける学習機能を機械学習のライブラリを用いずに丁寧に理解しようとした(後半)
https://qiita.com/Fumio-eisan/items/7507d8687ca651ab301d
さて、ロジスティック回帰における確率的勾配降下法のパラメータ更新式はこちらになります。
\begin{align}
w_{i+1}& = w_i -\eta・\frac{δE}{δw}\\
&= w_i -\eta・(y_n-t_n)φ(x_n)
\end{align}
この時、$w$は識別器のパラメータ、$\eta$は学習率、$y$がシグモイド関数によって得られる0~1の確率、$t$が0か1を示す教師データ、$φ(x)$が基底関数になります。
さらっと式変形を行いましたが、以下の変換ができることがロジスティック回帰特有の変形になります。
\frac{δE}{δw}=(y_n-t_n)φ(x_n)
ニューラルネットワーク等ではこの損失関数の勾配を求めることが非常に数学的に煩雑であったり、計算量が多くなることが懸念されます。従って、誤差逆伝搬法等の手法が用いられます。ロジスティック回帰においては、シグモイド関数の特性も用いながら案外簡単な式として表すことが可能です。
式変形に関しては、に関しては下記URLが非常に丁寧に解説されておりますので、ご参照頂けると幸甚です。
参考URL
http://gihyo.jp/dev/serial/01/machine-learning/0019
さて、実際に実装していくと下記のようになります。今回は学習率を最初は0.1としています。そして、収束しやすいように学習率を徐々に今回は低下させています。
# 学習率の初期値
eta = 0.1
for i in range(len(xlist)):
list = range(N)
for n in list:
x_n, y_n = X[n, :]
t_n = T[n]
# 予測確率
feature = phi(x_n, y_n)
predict = sigmoid(np.inner(w, feature))
w -= eta * (predict - t_n) * feature
# イテレーションごとに学習率を小さくする
eta *= 0.9
計算した結果を図示します。
# 散布図と予測分布を描画
plt.figure(figsize=(6, 6))
plt.imshow(zlist, extent=[-3,3,-3,3], origin='lower', cmap='GnBu')
plt.plot(X[T==1,0], X[T==1,1], 'o', color='red')
plt.plot(X[T==0,0], X[T==0,1], 'o', color='blue')
plt.show()
無事にランダムな点の青と赤の領域を分けることが可能な識別器を作成することができました。
終わりに
今回、自作でロジスティック回帰の判別器を作成しました。数学的に損失関数の最適化を行う方法をたどることが興味深いものでした。
プログラム全文はこちらにあります。
https://github.com/Fumio-eisan/logistic_20200411