はじめに
今回は、主成分分析と呼ばれる手法についてまとめます。この主成分分析はデータ解析の一手法です。昨今のビックデータを扱う上で有用な手段であるため、活用されています。
また、GANを初めとするニューラルネットワークにおけるオートエンコーダの考え方の基礎になります。私自身が勉強をしたいモチベーションはここにあります。
今回参考にした資料はこちらになります。**特にPRML本は記述が丁寧であったため、式の展開が追いやすく理解が進みました。**名著であることの理由が分かったような気がしました。
- パターン認識と機械学習 下 (通称PRML)
- Principal Component Analysis
http://cda.psych.uiuc.edu/statistical_learning_course/Jolliffe%20I.%20Principal%20Component%20Analysis%20(2ed.,%20Springer,%202002)(518s)_MVsa_.pdf
3.機械学習のための特徴量エンジニアリング ―その原理とPythonによる実践 (オライリー)
主成分分析ってなんだ
主成分分析(通称PCA;principal component analysis)とは、**変数がたくさんある場合にごく少数の新しい変数に置き換えることを指します。**別名として、Karhunen-Loeve変換とも言われるようです。
もう少し教科書の言い方をすると、主部分空間(principal subspace)と呼ばれる低次元への線形空間上への、データ点の直交射影のことになります。そして、この射影されたデータの分散が最大化されるように定めることがポイントです。また、データ点と射影した点の間の2乗距離の平均値で定義される射影のコスト関数の期待値を最小化すると定義することができます。この二つの考え方は等価です。
- 射影されたデータの分散最大化(Hotelling, 1933)
- 射影のコスト関数の期待値最小化(=残差の平方和の最小化)(Pearson, 1901)
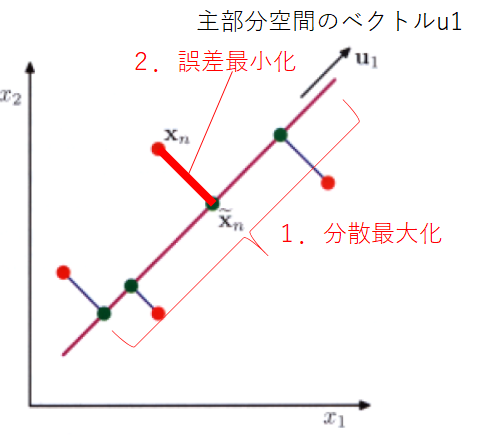
簡単に考え方を下記に示します。
1.の分散最大化は、元々の観測データで表現されているバラツキを損なわずに新しい次元で表現したいという思いからくる考え方です。2.のコスト関数の期待値最小化は、要は誤差をなるべく小さく表現する次元を探すということになります。1,2はそれぞれ異なる表現となっていますが結果として同義です。
分散最大化による定式化
次元$D$における観測データの集合{$\bf x_n$}$(n=1,2,....N)$を考えます。今回の目的は、射影されたデータ点の分散を最大化しながら、データを$M$次元(<$D$)の空間へ射影することです。
まず、1次元空間($D=1$)への射影を考えます。
1次元空間への射影
この1次元空間の方向を$D$次元のベクトル$\bf u_1$として表します(下記図)。
ここで、$\bf u_1$ベクトルは単位ベクトルと仮定します($\bf {u_1^T u_1}=1$)。これは、$u_1$自体の大きさに意味があるのではなく、定義される方向が重要であることと、計算しやすさのために行った手続きです。
そして、各データ点{$\bf x_n$}はスカラー値$\bf u_1^Tx_n$の上に射影されます。さて、分散を最大化することを考えるため、$\bar{x_n}$を平均値と置いて以下続きます。射影されたデータの分散は、
\begin{align}
&\frac{1}{n} \sum_{n=1}^{n} ||\mathbf{u_1}^T \mathbf{x_i} - \mathbf{u_1}^T \bar{\mathbf{x}}||^2 \\
= &\frac{1}{n} \sum_{n=1}^{n} ||\mathbf{u_1}^T (\mathbf{x_i} - \bar{\mathbf{x}})||^2 (式1)\\
= &\frac{1}{n} \sum_{n=1}^{n} \bigl( \mathbf{u_1}^T (\mathbf{x_i} - \bar{\mathbf{x}}) \bigr) \bigl( (\mathbf{x_i} - \bar{\mathbf{x}})^T \mathbf{u_1} \bigr) \\
= &\mathbf{u_1}^T \bigl( \frac{1}{n} \sum_{n=1}^{n} (\mathbf{x_i} - \bar{\mathbf{x}}) (\mathbf{x_i} - \bar{\mathbf{x}})^T \bigr) \mathbf{u_1} \\
= &\mathbf{u_1}^T \mathbf{S} \mathbf{u_1} \\
\end{align}
で与えられます。ここで$S$はデータ共分散行列であり、次のように定義されます。
\frac{1}{n} \sum_{n=1}^{n} (\mathbf{x_i} - \bar{\mathbf{x}}) (\mathbf{x_i} - \bar{\mathbf{x}})^T = \mathbf{S}
さて、射影された分散$\bf {u_1^T S u_1}$を$\bf u_1$に対して最大化することを考えます。ここで先ほどの前提に関係しますが、$||u_1||→∞$となることを避ける必要があります。従って、$\bf {u_1^T u_1}=1$を前提を置く必要があるのです。
この分散最大化を考えるうえで、ラグランジュの未定乗数法を適用します。このラグランジュの未定乗数法は、簡単にいうと最大値を求めることが難しい関数があるとします。直接最大値を求めることは難しいためこの求めたい関数と制約条件を合わせた新関数を定義します。その新関数の最小値が、元の関数の最大値となるように設計してあげることがポイントです。従って、新関数の最小値を求めることで元の関数の最大値を知ることができる、という流れになっています。
さて、実際に先ほどの式に対してラグランジュの未定乗数法を適用すると、$\lambda_1$をラグランジュの乗数として、
L(\mathbf{u_1}, \lambda_1) = \frac{1}{2} \mathbf{u_1}^T \mathbf{S} \mathbf{u_1} - \lambda_1 (\mathbf{u_1}^T \mathbf{u_1} - 1)
と表すことができます。
この関数の最小値を求めるには、$\bf u_1$で偏微分して$0$と置くことで求めることができますので、
\frac{\partial L}{\partial \mathbf{u_1}} = \mathbf{S} \mathbf{u_1} - \lambda_1 \mathbf{u_1} = 0 \\
\mathbf{S} \mathbf{u_1} = \lambda_1 \mathbf{u_1} \ (式1)\\
と変形することができます。$\bf u_1$は
||\bf S -\lambda_1 I|| =0
の行列式を解くことで求めることができます。
また先ほどの式1について、左から$\bf u_1^T$を掛けて、$\bf {u_1^T u_1}=1$を適用すると分散は、
\mathbf{u_1}^T \mathbf{S} \mathbf{u_1} = \lambda_1
と求めることができます。
従って、分散は$\bf u_1^T$を最大固有値$\lambda_1$に属する固有ベクトルに選んだ時に最大になることが分かります。この固有ベクトルは第一主成分と呼ばれます。
実装上での主成分分析のやり方
さて、上記で1次元に射影した場合の主成分分析を考えました。一般的に、M次元の空間への射影を考えます。この時、実は元のデータ集合{$\bf x_n$}$(n=1,2,....N)$の行列を特異値分解することで簡単に求めることが可能になります。
特異値分解とは、行列における操作のことで、下記に概要及び実装の仕方を記しています。
GANの安定性に寄与しているというSpectral Normalizationや特異値分解について頑張って理解しようとした
https://qiita.com/Fumio-eisan/items/54d138df12737c0984b2
残差の平方和の最小化を求める
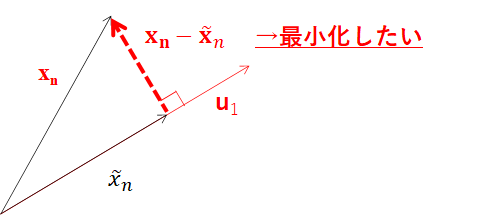
さて、続いてもう一つの考え方である残差の平方和の最小化という観点から主成分分析を考えます。
平方和とは上記図における$x_n-\bf \tilde {x_n}$なります。$\bf \tilde {x_n}$を$\bf {x_n}$と$\bf u_1$を用いて表現します。$\bf \tilde {x_n} = t\bf u_1 $と置いたとき、
\bf u_1^T (\bf x_n -t \bf u_1) =0
を解くと、
\bf u^T \bf x_n -t\bf u_1^T \bf u_1 =0
t = \bf u_1^T \bf {x_n}
(\bf u_1^T \bf u =1のため)
と解くことができます。従って、$(\bf u_1^T \bf {x_n})\bf u_1$が正射影となります。
つまり最初に求めたかった$\bf x_n-\bf \tilde {x_n}$は、$\bf x_n-(\bf u_1^T \bf {x_n})\bf u_1$となります。この長さの平方和を最小化するような$\bf u_1$を考えると、
\sum_{n=1}^{N} ||\bf x_n-(\bf u_1^T \bf {x_n})\bf u_1||^2 \\
と立式することができます。
これを解いていくと
||\bf x_n-(\bf u_1^T \bf {x_n})\bf u_1||^2 = \bf x_n^T \bf x_n - (\bf u_1^T \bf {x_n})^2
となります。$\bf x_n^T \bf x_n $は$\bf u_1$が変わっても一定あるため、この最小化問題は
\sum_{n=1}^{N} -(\bf u_1^T \bf {x_n})^2
を解くことと同義となります。これは、最大化問題を解くうえで式1と同じこと示しています。先ほどは平均値との差を決めていましたが、今回のケースは平均値を予め引いたものと解釈すると同義といえます。
つまり、先ほどの最大値問題が今回はマイナスが付いているために最小化問題となっているだけであることがいえました。続きは最大値を求める場合と一緒になります。
雑感:製造業へ主成分分析の展開を考える
私は、製造業にて生産技術者として働いています。その中で、生産ロス(=機会損失)に繋がる一因として機械装置の突発トラブルがあります。これは、予期していないタイミングで装置が通常の運転をしなくなるため起こってしまいます。
トラブルにより生産活動が止まってしまう重要な装置の場合は、基本的に時間基準保全(Time Based Maintenance)の考えに基づいて定期的に修繕行為を行っています。
この期間は基本的に修繕すべき部品(=重要保安部品)のメーカー推奨交換時期よりも、**早いタイミング(=前倒しの期間)で置くことが多いです。**つまり、既に安全側の期間となっているものの、これでも時期を待たずしてトラブルが起こってしまう場合があります。起こってしまう理由に関しては、場合によって原因がまちまちなので一概に言えませんが、生産している製品の種類が変わったり、それを操作する作業者が変わったりといったことが挙げられます。
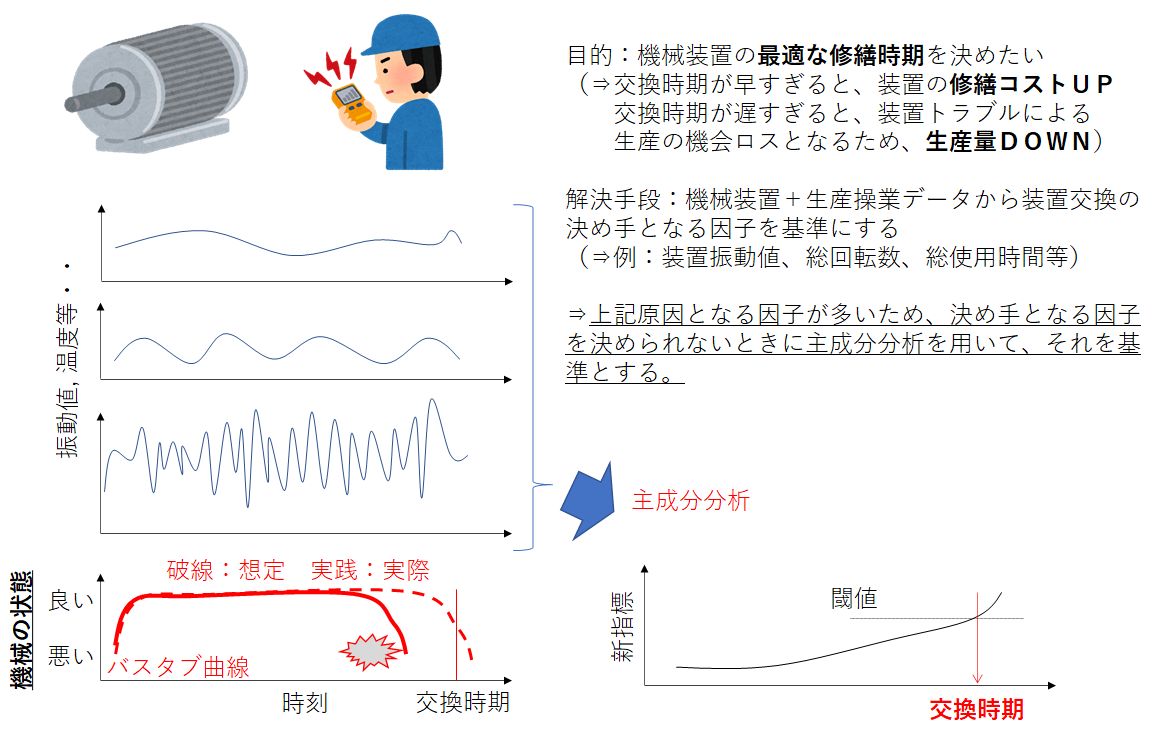
この課題に対して、主成分分析の応用を考えます。下記に課題から解決に至るマンガ絵を記しています。
昨今のIoT化により装置へのセンサー取り付け・データ取得が盛んになっています。また、生産に関わる操業データも同様に活用しやすい(=データを取得しやすい)状況になっています。
こうした背景から大量のデータから装置の故障予測を行うことができます。この予測を行う上で、基準となる因子の決定や閾値を決めることが課題となります。
多くの因子から少ない因子に絞るプロセスに主成分分析が応用できると思います。例えば、装置振動数×総使用時間等の複合的な因子を関係させた新しい指標を用いることが考えられます。
但し、ここでのポイントはドメイン知識と呼ばれるその装置、生産関係の知識から考えたときに妥当であるかという点を考えなければなりません。
例えば、この圧延機に設置されたモーターであれば振動数が元々〇~〇Hzであれば通常の振動である。あるいは、△hz以上になると交換時期に近い、などといったものです。知識・経験がここで決めた因子に対して妥当性を与えることになります。
結局、現場を何十回、何百回と見て回った現場の作業者の方の知識・経験がまだまだ重要であることは変わりないと思っています。
もう一つのポイントです。この考え方を適用する上での課題は、装置へのセンサー取り付ける必要がある、妥当なデータが得られるセンサーが付いているか、といったハード側の課題がまだまだ大きいように感じます。工場自体に計装品が十分に設置されていない場合があったり、設置されていたとしてもデータ収集ができるシステム構成になっていない等があります。従い、解析を行いたい対象からデータを取得する手段がないところで止まっているのです。
昨今、機械学習の考え方だけが先行していて、ハード側が付いてきていないことが実情としてあるように感じています。。従い、そのメーカーの設備技術者及びIT担当者、ITコンサルの方々の泥臭いながらも製造実力向上に必要な取り組みとなっているのです。
おわりに
主成分分析の手法をまとめました。数学的な操作は単純であるものの、応用の幅の広さを感じました。個人的には画像処理に使っている場面をより学んで理解していきたいと思っています。