統計とR言語の勉強をしています。
「Rによるやさしい統計学」の写経で勉強。
実行環境
- Windows10 Pro 64bit
- R:3.4.3
- RStudio:1.1.383
RStudioのConsoleを使って実行しています
不偏分散と標本分散について
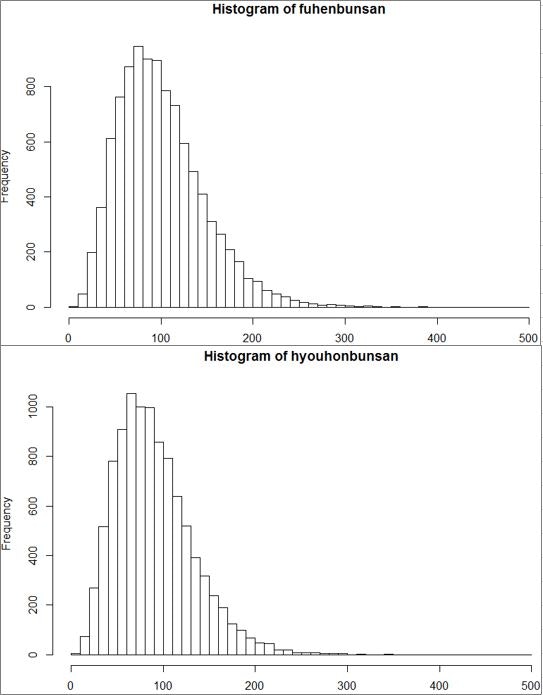
分散推定を下記のようにシミュレーションすると不偏分散の方が母分散の100に近いのがわかります。ヒストグラムで見ると、不偏分散の方が値が大きくなりやすいです(分母が小さいので当然です)。
hyouhonbunsan <- numeric(length=10000) #推定値を格納
fuhenbunsan <- numeric(length=10000) #推定値を格納
for(i in 1:10000){
hyouhon <- rnorm(n=10, mean=50, sd=10)
hyouhonbunsan[i] <- mean((hyouhon-mean(hyouhon))^2) #標本分散
fuhenbunsan[i] <- var(hyouhon) #不偏分散
}
> mean(hyouhonbunsan)
[1] 90.01698
> mean(fuhenbunsan)
[1] 100.0189
> hist(hyouhonbunsan,breaks=seq(0,500,10))
> hist(fuhenbunsan,breaks=seq(0,500,10))
検定
区間推定の記事参照
母分散が既知の場合の平均値検定
以下の前提だとして、Rで検定します。
| 項目 | 内容 |
|---|---|
| 前提 | 心理学テストの特典は平均12、分散10の正規分布に従う。今回実施した20人の心理学テスト結果は同じ母集団からの無作為標本か? |
| 帰無仮説 | $\mu = 12$:心理学テストの母平均は12 |
| 対立仮説 | $\mu \ne 12$:心理学テストの母平均は12でない |
| 検定統計量 | $\frac{\overline{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}$ |
| 有意水準 | 5% |
| 母集団分布 | N(12, 10):正規分布の平均12と分散10 |
まずは、検定統計量を算出します。
> shinrigaku_test <- c(13, 14, 7, 12, 10, 6, 8,15, 4, 14, 9, 6, 10, 12, 5, 12, 8, 8, 12, 15)
> zbunshi <- mean(shinrigaku_test) - 12 #検定統計量の分子
> zbunbo <- sqrt(10/length(shinrigaku_test)) #検定統計量の分母
> zstat <- zbunshi/zbunbo #検定統計量
> zstat
[1] -2.828427
今回は有意水準5%は、両側検定なので上側と下側での棄却域をqnorm関数で算出します。先に求めた-2.828427は下側の-1.959964以下なので帰無仮説は棄却され、対立仮説「心理学テストの母平均は12でない」が採択されます。
> qnorm(0.025) #下側
[1] -1.959964
> qnorm(0.975) #上側
[1] 1.959964
> qnorm(0.025, lower.tail=FALSE) #上側(別解)
[1] 1.959964
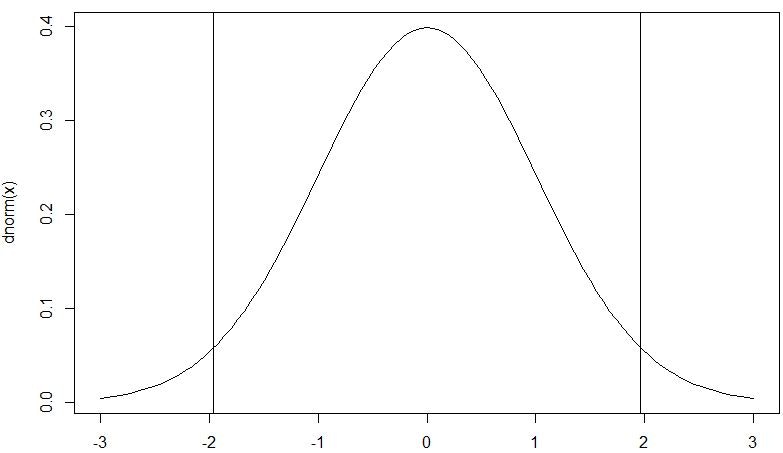
ちなみに以下のコードで正規分布の図に棄却域部分の縦棒を追加したグラフを出力することができます。
> curve(dnorm(x),-3,3)
> abline(v=qnorm(0.025))
> abline(v=qnorm(0.975))
また、関数pnormを使って検定統計量からp値を求めることができます。lower.tailオプションを使うことで上側確率を計算できます。今回は両側検定なので2倍することが必要です。
> pnorm(-2.828427)
[1] 0.002338868
> pnorm(2.828427, lower.tail = FALSE)
[1] 0.002338868
> 2*pnorm(2.828427, lower.tail = FALSE)
[1] 0.004677737
母分散が未知の場合の平均値検定
先程と同じ設問ですが、母分散が未知の場合とします。
| 項目 | 内容 |
|---|---|
| 前提 | 心理学テストの得点は平均12の正規分布に従う。今回実施した20人の心理学テスト結果は同じ母集団からの無作為標本か? |
| 帰無仮説 | $\mu = 12$:心理学テストの母平均は12 |
| 対立仮説 | $\mu \ne 12$:心理学テストの母平均は12でない |
| 検定統計量 | $\frac{\overline{X}-\mu}{\sqrt{\frac{S^2}{n}}}$ |
| 有意水準 | 5% |
| 母集団分布 | N(12, ?):正規分布の平均12と分散未知 |
まずは、検定統計量を算出します。
> tbunshi <- mean(shinrigaku_test) - 12 #検定統計量の分子
> tbunbo <- sqrt(var(shinrigaku_test)/length(shinrigaku_test)) #検定統計量の分母
> tstat <- tbunshi/tbunbo #検定統計量
> tstat
[1] -2.616648
qt関数で上側と下側での棄却域を自由度19のt分布で算出します。先に求めた-2.616648は下側の-2.093024以下なので帰無仮説は棄却され、対立仮説「心理学テストの母平均は12でない」が採択されます。
> qt(0.025, 19) #下側
[1] -2.093024
> qt(0.975, 19) #上側
[1] 2.093024
> qt(0.025,19,lower.tail = FALSE) #上側(別海)
[1] 2.093024
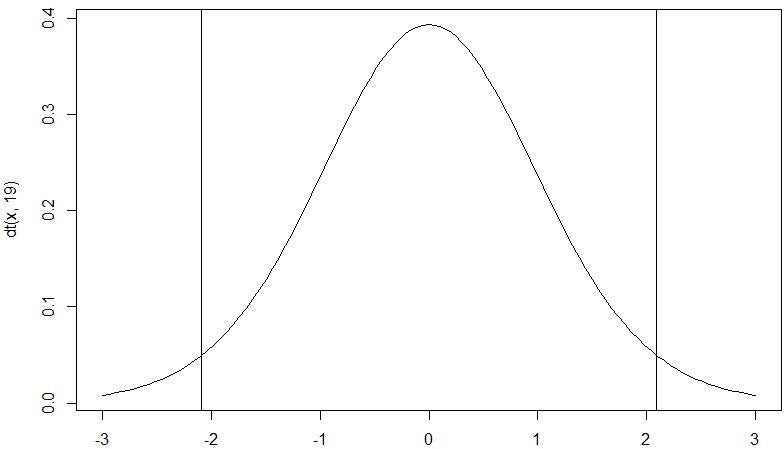
以下のコードでt分布の図に棄却域部分の縦棒を追加したグラフを出力することができます。
> curve(dt(x,19),-3,3)
> abline(v=qt(0.025,19))
> abline(v=qt(0.975,19))
関数ptを使って検定統計量からp値を求めることができます。lower.tailオプションを使うことで上側確率を計算できます。今回は両側検定なので2倍することが必要です。
> pt(-2.616648,19)
[1] 0.00848546
> pt(2.616648,19,lower.tail = FALSE)
[1] 0.00848546
> 2*pt(2.616648,19,lower.tail = FALSE)
[1] 0.01697092
ここまで地道に計算しましたが、t分布での検定はt.test関数を使えば一発で検定できるので便利です!
> t.test(shinrigaku_test,mu=12)
One Sample t-test
data: shinrigaku_test
t = -2.6166, df = 19, p-value = 0.01697
alternative hypothesis: true mean is not equal to 12
95 percent confidence interval:
8.400225 11.599775
sample estimates:
mean of x
10
無相関検定
帰無仮説を「母集団において相関が0である」とする検定を無相関検定と呼びます。以下の例題でRで検定します。
| 項目 | 内容 |
|---|---|
| 前提 | 統計テスト1と統計テスト2の得点の相関係数の検定を実施 |
| 帰無仮説 | $\rho = 0$:母相関は0 |
| 対立仮説 | $\rho \ne 0$:母相関は0ではない |
| 検定統計量 | $\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}$ |
| 有意水準 | 5% |
まずは、検定統計量を算出します。
> statistics_test1 <- c(6, 10, 6, 10, 5, 3, 5, 9, 3, 3, 11, 6, 11, 9, 7, 5, 8, 7, 7, 9)
> statistics_test2 <- c(10, 13, 8, 15, 8, 6, 9, 10, 7, 3, 18, 14, 18, 11, 12, 5, 7,12, 7, 7)
> hyouhon_soukan <- cor(statistics_test1,statistics_test2)
> hyouhon_soukan
[1] 0.749659
> sample_size <- length(statistics_test1)
> tbunshi <- hyouhon_soukan*sqrt(sample_size-2)
> tbunbo <- sqrt(1 - hyouhon_soukan^2)
> tstat <- tbunshi/tbunbo
> tstat
[1] 4.805707
qt関数で上側と下側での棄却域を自由度18のt分布で算出します。先に求めた4.805707は上側の2.100922以上なので帰無仮説は棄却され、対立仮説「母相関は0ではない」が採択されます。もちろんpt関数を使って求めても大丈夫です。
> qt(0.025, 18) #下側
[1] -2.100922
> qt(0.975, 18) #上側
[1] 2.100922
ここまで地道に計算しましたが、無相関検定はcor.test関数を使えば一発で検定できるので便利です!
> cor.test(statistics_test1,statistics_test2)
Pearson's product-moment correlation
data: statistics_test1 and statistics_test2
t = 4.8057, df = 18, p-value = 0.0001416
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.4596086 0.8952048
sample estimates:
cor
0.749659
独立性検定
2つの質的変数が独立であるかを確かめます。以下の例題でRで検定します。
| 項目 | 内容 |
|---|---|
| 前提 | 数学の好き/嫌い、統計の好き/嫌いのアンケート結果に連関があるか |
| 帰無仮説 | 2つの変数は独立(2つの変数は連関がない) |
| 対立仮説 | 2つの変数は連関がある |
| 検定統計量 | $\sum_{i=0}^n\frac{(O_k-E_k)^2}{E_n}$ O:観測度数、E:期待度数 |
| 有意水準 | 5% |
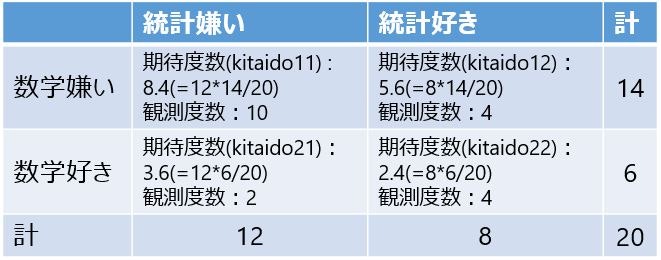
こんなクロス集計表があったとします(観測度数から計算される期待度数を付記しておきました)。
まずは、検定統計量を算出します。
# 期待度数計算
> kitaido11 <- 12*14/20
> kitaido21 <- 12*6/20
> kitaido12 <- 8*14/20
> kitaido22 <- 8*6/20
> kitaidosu <- c(kitaido11,kitaido21,kitaido12,kitaido22)
# 観測度数格納
> kansokudosu <- c(10,2,4,4)
> kansokudosu
[1] 10 2 4 4
# カイ二乗要素と検定統計量(カイ二乗和)
> chisq_factor <- (kansokudosu-kitaidosu)^2/kitaidosu
> chisq_factor
[1] 0.3047619 0.7111111 0.4571429 1.0666667
> chi_jijo <- sum(chisq_factor)
> chi_jijo
[1] 2.539683
qchisq関数で棄却域を自由度1のカイ二乗分布で算出します。先に求めた2.539683は上側の3.841459以下なので帰無仮説「2つの変数は独立」は採択されます。
> qchisq(0.95,1)
[1] 3.841459
関数pchisqを使って検定統計量からp値を求めることができます。lower.tailオプションを使うことで上側確率を計算できます。
> pchisq(2.539683,1,lower.tail = FALSE)
[1] 0.1110171
ここまで地道に計算しましたが、独立検定はtable関数を使ったクロス集計表の変数でchisq.test関数を使えば一発で検定できるので便利です!
> math <- c("嫌い","嫌い","好き","好き","嫌い","嫌い","嫌い","嫌い","嫌い","好き","好き","嫌い","好き","嫌い","嫌い","好き","嫌い","嫌い","嫌い","嫌い")
> stat <- c("好き","好き","好き","好き","嫌い","嫌い","嫌い","嫌い","嫌い","嫌い","好き","好き","好き","嫌い","好き","嫌い","嫌い","嫌い","嫌い","嫌い")
> cross_syukei <- table(math,stat)
> chisq.test(cross_syukei,correct=FALSE)
Pearson's Chi-squared test
data: cross_syukei
X-squared = 2.5397, df = 1, p-value = 0.111
Warning message:
In chisq.test(cross_syukei, correct = FALSE) :
カイ自乗近似は不正確かもしれません