筆者自身の統計勉強用備忘録です。各種分布と区間推定、検定についてメモ書きしています。
グラフはRを使って出力しています。
分布
カイ二乗分布
独立に標準正規分布に従う k 個の確率変数 $X_1$,$X_2$,..., $X_k$ をとる。その2乗総和の確率変数が自由度 k のカイ二乗分布と呼ぶ。詳しくはWikipediaを見ましょう。
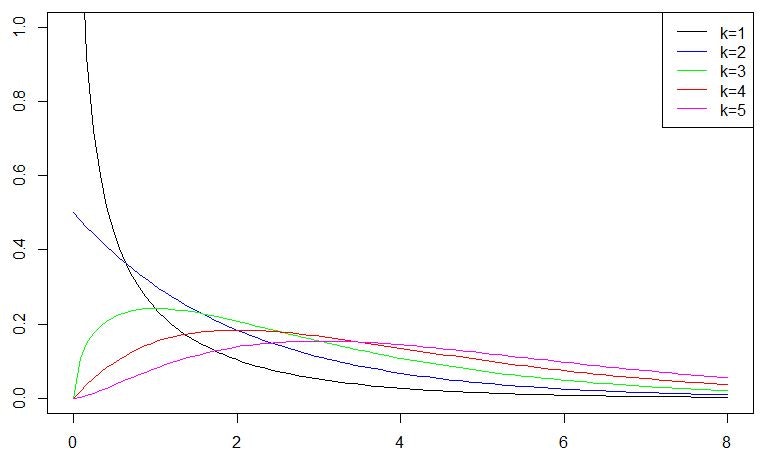
R言語で分布をグラフ出力してみました。
※Rでカイ二乗分布の確率密度関数のグラフをシミュレーション的に描くをかなり参考にしています。
2乗しているので、X軸に負の値がありません。自由度に応じて分布が大きく変わっているのがわかりません。自由度1は標準正規分布の2乗なので、想像がつきやすいです。
自由度kのカイ二乗分布出力用R言語コード
curve(dchisq(x,1), xlim=c(0,8), ylim=c(0,1), col="black", ylab="dchisq(x, k)")
curve(dchisq(x,2), xlim=c(0,8), ylim=c(0,1), col="blue" , add=T)
curve(dchisq(x,3), xlim=c(0,8), ylim=c(0,1), col="green" , add=T)
curve(dchisq(x,4), xlim=c(0,8), ylim=c(0,1), col="red" , add=T)
curve(dchisq(x,5), xlim=c(0,8), ylim=c(0,1), col="magenta", add=T)
#凡例
legend( "topright", lty=1,
legend = c("k=1" , "k=2" , "k=3" , "k=4", "k=5"),
col = c("black", "blue", "green", "red", "magenta") )
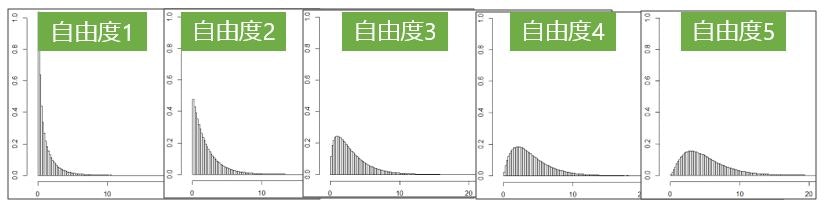
R上で標準正規分布からヒストグラム出力しても同じようなグラフになるのがわかります。
カイ二乗分布をヒストグラムから作成(自由度5の場合)
n <- 1000000
Z <- (rnorm(n))^2 + (rnorm(n))^2 + (rnorm(n))^2 + (rnorm(n))^2 + (rnorm(n))^2
hist(Z, breaks=seq(0, 40, 0.2), freq=F, ylim=c(0,1))
t分布
t分布、またはスチューデントのt分布と呼ばれます。
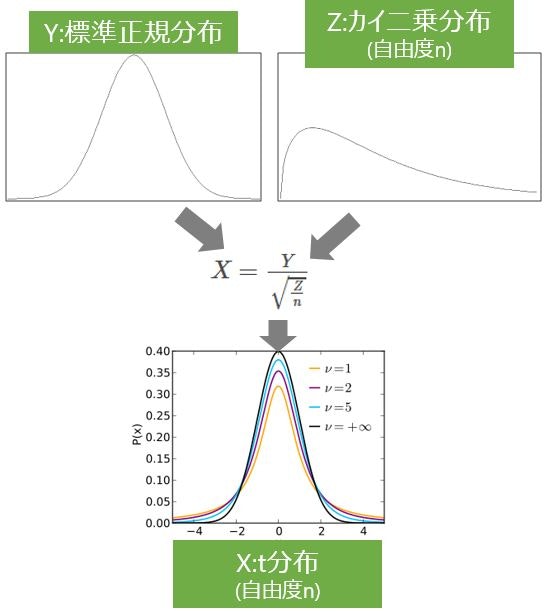
2つの独立した変数YとZがあり、Yは標準正規分布に従い、Zは自由度nのカイ二乗分布に従うものとする。このとき、確率変数Xを$X=\frac{Y}{\sqrt{\frac{Z}{n}}}$とおくと、Xは自由度nのt分布に従う。
wikipediaリンク
F分布
F分布またはフィッシャー分布と呼ばれます。
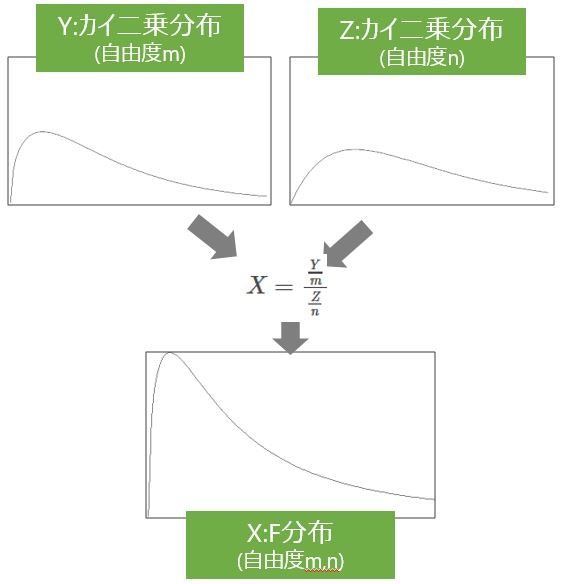
2つの独立した変数YとZがあり、Yは自由度mの、Zは自由度nのカイ二乗分布に従うものとする。このとき、確率変数Xを$X=\frac{\frac{Y}{m}}{\frac{Z}{n}}$とおくと、Xは自由度(m,n)のF分布に従う。
区間推定
母平均、母分散の区間推定パターンは以下のとおりです。
| 推定対象 | 母分散 | 確率変数 | 確率変数の分布 | 区間推定計算式(信頼係数$1-\alpha$) |
|---|---|---|---|---|
| 母平均 | 既知 | $\frac{\overline{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}$ | 標準正規分布 | $\overline{X}-z(\frac{\alpha}{2})\sqrt{\frac{\sigma^2}{n}}\leqq\mu\leqq\overline{X}+z(\frac{\alpha}{2})\sqrt{\frac{\sigma^2}{n}}$ |
| 母平均 | 未知 | $\frac{\overline{X}-\mu}{\sqrt{\frac{S^2}{n}}}$ $S^2$は母分散不偏推定量 |
自由度(n-1)t分布 | $\overline{X}-u_{n-1}(\frac{\alpha}{2})\sqrt{\frac{S^2}{n}}\leqq\mu\leqq\overline{X}+u_{n-1}(\frac{\alpha}{2})\sqrt{\frac{S^2}{n}}$ |
| 母分散 | 未知 | $\sum_{i=1}^n (\frac{X_i-\overline{X}}{\sigma})^2$ | 自由度(n-1)$\chi^2$分布 | $\frac{(n-1)S^2}{v_{n-1}(\frac{\alpha}{2})}\leqq\sigma^2\leqq\frac{(n-1)S^2}{v_{n-1}(1-\frac{\alpha}{2})}$ |
検定
2つの正規分布に従う母集団から無作為に抽出した大きさm, n の2組の標本
| 推定対象 | 母分散 | 確率変数 | 確率変数の分布 |
|---|---|---|---|
| 母平均の差 | 既知 | $\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_{x}^2}{m}+\frac{\sigma_{y}^2}{n}}}$ | 標準正規分布 |
| 母平均の差 | 未知 | $\frac{\overline{X}-\overline{Y}}{\sqrt{(\frac{1}{m}+\frac{1}{n}){S_{xy}}^2}}$ ${S_{xy}}^2=\frac{1}{m+n-2}[\sum_{i=0}^m(X_i-\overline{X})^2+\sum_{i=0}^n(Y_i-\overline{Y})^2]$ |
自由度(m+n-2)のt分布 |
| 母分散の差 | 未知 | $\frac{{S_x}^2}{{S_y}^2}$ ${S_{x}}^2=\frac{1}{m-1}\sum_{i=0}^m(X_i-\overline{X})^2$ ${S_{y}}^2=\frac{1}{n-1}\sum_{i=0}^n(Y_i-\overline{Y})^2$ |
自由度(m-1,n-1)のF分布 |