【Python】ゴールデンクロス・デッドクロス売買手法のSMA日数をベイズ最適化してみた

こんにちは，藤野です．

普段はこちらで株式投資に関するブログを書いています．

今回は，『ゴールデンクロス・デッドクロスで売買を判断する手法のバックテスト』に対して，『手法をベイズ最適化』してみます．

バックテストについて

以前書いた記事

を基本として行います．

この記事では最適化は『Backtesting.py』のoptimize機能を用いましたが，ここを今回はベイズ最適化でやってみようということです．

※注意！
最後で述べるように，Backtesting.pyでもベイズ最適化で探索できるようです（Backtesting.pyのoptimize機能との比較）．自作部分は無駄骨になった気がするので，この部分だけ読んでいただいても構いません．

ベイズ最適化について

ベイズ最適化はちょっと雑な手法ですが汎用性は高く，ブラックボックスを最適化するときには手軽で便利です．

ただし，汎用性が高いということは精度にはあまり期待できないということなので，多少目をつぶる必要がありますね．

なぜベイズ最適化で手法を最適化するのか？と言われたら，何となくです．
ほとんどの場合はBacktesting.pyのoptimize機能を使った方が総合的には良い気がしますが，探索範囲が広い場合はベイズ最適化の方が（計算時間の面で）有利になる可能性があるかな～と思っています．ただし，今回のような変数が2つしかなく範囲が狭い場合にはベイズ最適化は微妙でしょう．

ベイズ最適化についてのソースコードは，以下の記事を参考にしました．

この記事では，Pythonライブラリbayes_optの『Bayesian Optimization』で基本的な関数をベイズ最適化しています．

ソースコード

必要なライブラリ

最初に，必要なライブラリを紹介しておきます．

#データ取得用
import pandas_datareader.data as web
import datetime

# バックテスト用
from backtesting import Backtest, Strategy
from backtesting.lib import crossover
from backtesting.test import SMA # SMAインジケータ

#ベイズ最適化用
from bayes_opt import BayesianOptimization

#グラフ描画用
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import numpy as np

データ取得用ライブラリpandas_datareader，
バックテスト用ライブラリbacktesting，
ベイズ最適化用ライブラリbayes_opt
はpipでインストールできると思います．

もちろん，グラフ描画用のライブラリもpipでインストールできると思います．

ソースコードの構成

想像ついているかもしれませんが，こんな感じになっています．

・データ取得部分
・バックテスト部分（SMAの日数を変数とする関数）
・ベイズ最適化部分（SMAの日数を変数としてバックテストの最終資産額を最大化する）
・出力部分（データやグラフ描画など）

つまり，SMAの日数をパラメータとしてベイズ最適化で調整し，バックテストの結果を良くします．

今回は冒頭のバックテストとベイズ最適化の記事をそのまま組み合わせただけなので不格好なコードになっていますが，ご了承ください．わかりずらいところがあれば，冒頭の2つの記事をご覧いただければと思います．

データ取得部分

今回は，2018/1/1~現在までのAAPL（Apple）の株でバックテストしたいと思います．

import pandas_datareader.data as web
import datetime

start = datetime.date(2018,1,1)
end = datetime.date.today()
data = web.DataReader('AAPL', 'yahoo', start, end)

バックテスト部分

from backtesting import Backtest, Strategy # バックテスト
from backtesting.lib import crossover
from backtesting.test import SMA # SMAインジケータ

def backtesting(x1, x2):

    print('x1 :', x1, 'x2 :', x2)

    class SmaCross(Strategy):
        n1 = int(x1) # 短期SMA
        n2 = int(x2) # 長期SMA

        def init(self):
            self.sma1 = self.I(SMA, self.data.Close, self.n1) 
            self.sma2 = self.I(SMA, self.data.Close, self.n2)

        def next(self): #チャートデータの行ごとに呼び出される
            if crossover(self.sma1, self.sma2): #sma1がsma2を上回った時
                self.buy() # 買い
            elif crossover(self.sma2, self.sma1):
                self.position.close() # 売り

    # バックテストの設定
    bt = Backtest(
        data, # チャートデータ
        SmaCross, # 売買戦略
        cash=1000, # 最初の所持金
        commission=0.00495, # 取引手数料
        margin=1.0, # レバレッジ倍率の逆数（0.5で2倍レバレッジ）
        trade_on_close=True, # True：現在の終値で取引，False：次の時間の始値で取引
        exclusive_orders=True #自動でポジションをクローズ
    )

    output = bt.run() # バックテスト実行
    score = output['Equity Final [$]']

    print('Equity :', score)

    return score

この関数backtesting(x1, x2)に短期SMAの日数x1と長期SMAの日数x2を入れれば，バックテスト行い，その最終資産額(Equity Final)scoreが返ってきます(このコードの参考はこちら)．

最初の所持金は1000です．

ただし，SMAを計算するときの日数は離散値（整数）である必要がある一方，ベイズ最適化で決められる変数は連続値なので，int形に変えています（今思ったら，焼きなまし法や遺伝的アルゴリズムとかの方がいいかもですね）．

ベイズ最適化部分

from bayes_opt import BayesianOptimization

x1_max, x1_min = 50, 1
x2_max, x2_min = 50, 1

# 探索するパラメータと範囲を決める
pbounds = {'x1': (x1_min, x1_max), 'x2': (x2_min, x2_max), }

# 探索対象の関数と、探索するパラメータと範囲を渡す
bo = BayesianOptimization(f=backtesting, pbounds=pbounds)
# 最大化する
bo.maximize(init_points=10, n_iter=90)

print('OPTIMIZE: END')

このコードの参考はこちら

グラフ描画部分

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

def plot_bo(bo):
    # プロット範囲
    X1 = [x1 for x1 in np.arange(x1_min, x1_max, 0.1)]
    X2 = [x2 for x2 in np.arange(x1_min, x2_max, 0.1)]
    X1, X2 = np.meshgrid(X1, X2)

    # サンプル点
    xs1 = [bo.res[p]['params']['x1'] for p in range(len(bo.res))]
    xs2 = [bo.res[p]['params']['x2'] for p in range(len(bo.res))]
    ys = [bo.res[p]['target'] for p in range(len(bo.res))]
    ax.scatter(xs1,xs2, ys, c='black', s=20, zorder=10, label='sample')

    # 最大値
    print(bo.max)
    max_x1 = bo.max['params']['x1']
    max_x2 = bo.max['params']['x2']
    max_y = bo.max['target']
    print('max = ', max_x1, max_x2, max_y)
    for y in range(0, int(max_y)): #stick
        ax.scatter([max_x1],[max_x2], y , c='green', s=1)
    ax.scatter([max_x1],[max_x2],[max_y], c='green', s=100, zorder=10, label='pred_max')

# 結果をグラフに描画する
plot_bo(bo)
# グラフを表示する
plt.legend()
plt.grid()
plt.show()

数値（最適化した変数と最終資産額）だけほしい場合は，このプロット関数は削除して実行してください．

このコードの参考はこちら

実行結果

上のコードをつなげて実行すると，以下のような結果が返ってきます．

|   iter    |  target   |    x1     |    x2     |
-------------------------------------------------
x1 : 37.66353427296505 x2 : 14.157903298750782
Equity : 1100.8355291460039
|  1        |  1.101e+0 |  37.66    |  14.16    |
x1 : 38.92713935929554 x2 : 20.254010912860902
Equity : 1141.707941385269
|  2        |  1.142e+0 |  38.93    |  20.25    |

…省略…

x1 : 44.74003561193411 x2 : 34.11890155066235
Equity : 1213.072423604965
|  99       |  1.213e+0 |  44.74    |  34.12    |
x1 : 11.844632007981543 x2 : 40.51328479597231
Equity : 2291.453910270881
|  100      |  2.291e+0 |  11.84    |  40.51    |
=================================================
OPTIMIZE: END
{'target': 3589.1827172409053, 'params': {'x1': 18.67976663100892, 'x2': 27.0708821014915}}
max =  18.67976663100892 27.0708821014915 3589.1827172409053

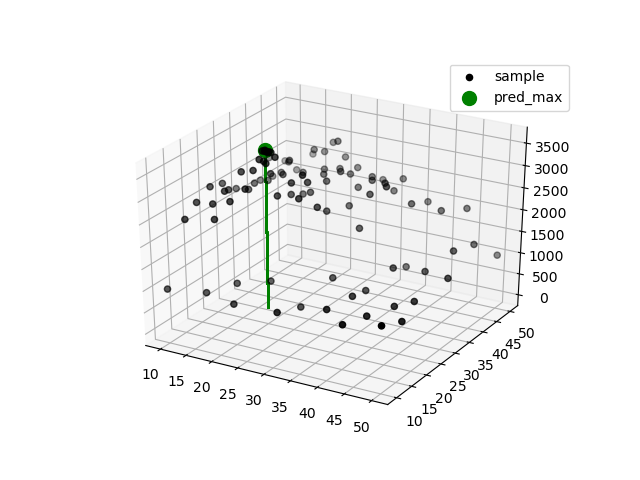
グラフのx,y軸はx1,x2の値で，z軸が最終資産額です．
また，緑の場所が最適解です．

短期SMAの日数x1 : 18日
長期SMAの日数x2 : 27日
最終資産額 : 3589
となりました．

2018年からの3年間で資産額が1000 → 3589ですから，さすがApple株！という感じです．

2018年1月1日にApple株を買って最後に売るときと同じかそれ以上のリターンとなっているので，山と谷を利用した良い売買であると言えるかもしれません．

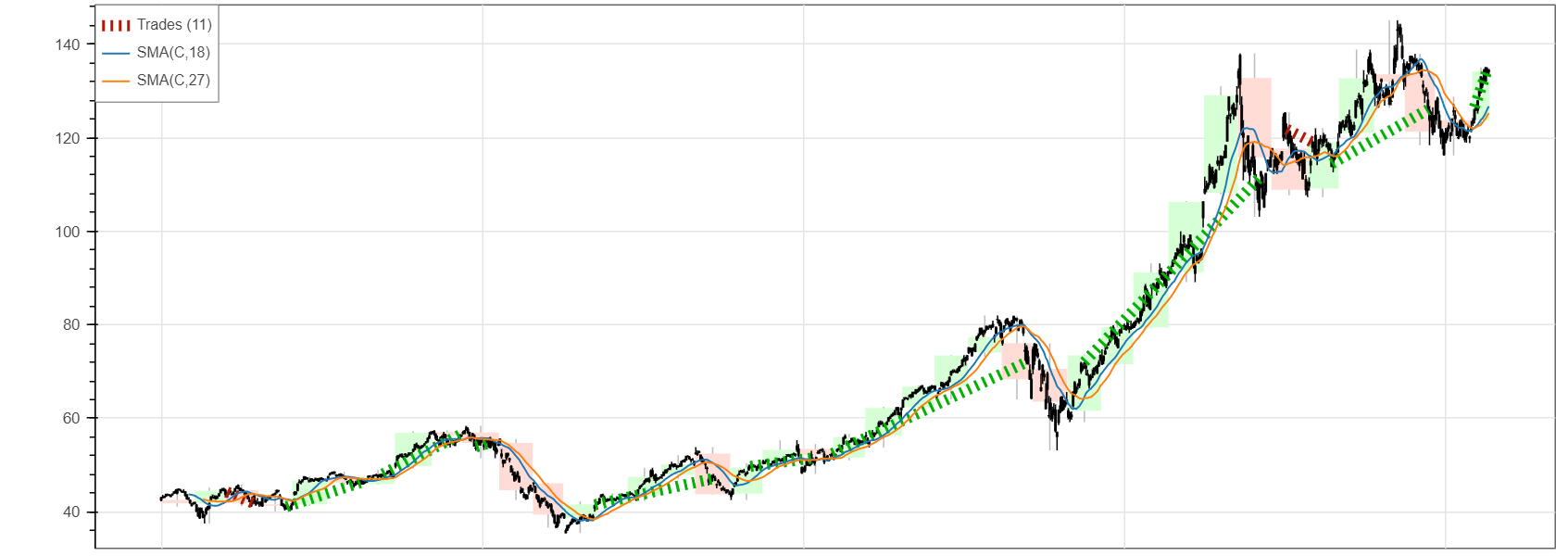
ちなみに，この日数でバックテストを行ったときの様子を描画すると以下のような感じです．

Backtesting.pyのoptimize機能との比較

さて，これがどれくらいいい結果なのか？をBacktesting.pyのoptimize機能と比較してみていきたいと思います．

Backtesting.pyでは，以下のように書くことで最終資産額を最適化できます．変数の範囲は先ほどと同じにしてあります(これを実行するには，こちらの記事をApple株に変えると楽です)．

手法は，グリッドサーチで探索します．

#Backtesting.pyによる手法最適化
output2=bt.optimize(n1=range(1, 50, 1),n2=range(1, 50, 1), maximize='Equity Final [$]', method='grid')
print(output2)
bt.plot()

結果は以下のようになりました（コードによるの結果の一部だけ表示しています）．

method : grid
短期SMAの日数x1 : 18日
長期SMAの日数x2 : 30日
最終資産額 : 3600

少しだけですが，リターンが増加しました．

ちなみに，Backtesting.pyのドキュメントを読むと，以下のように書いてありました．

"grid" which does an exhaustive (or randomized) search over the cartesian product of parameter combinations

gridは「包括的に(またはランダム)に」探索すると書いてあります．
また，上の最適化計算実行時には，以下のような警告が出ました．

UserWarning: Searching for best of 2401 configurations.
output = _optimize_grid()

探索範囲が広すぎると，全探索ではなく自動でそれよりも少ない回数でランダムに探索するようになっているのかもしれません．

では，もう一つの最適化手法『skopt』を使ってみます．

skoptは結局のところベイズ最適化を行っているみたいなので（参考），あまり比較にはならない気がしますが，ベイズ最適化の精度を確認する意味はあると思いますのでやってみます．

skoptを使用するには，以下のインストールが必要です．

pip install scikit-optimize

最適化の実行は，method以外は先ほどと同様です．

#最適化
output2=bt.optimize(n1=range(1, 50, 1),n2=range(1, 50, 1), maximize='Equity Final [$]', method='skopt')
print(output2)
bt.plot()

結果は以下のようになりました．

method : skopt
短期SMAの日数x1 : 18日
長期SMAの日数x2 : 27日
最終資産額 : 3921

最初に行ったベイズ最適化の結果と同じ値がでました．

MACDを最適化

今回は2本のSMAでバックテストを行い最適化しましたが，同様にして以下のようにMACDバージョンなどもできます．

反省

Apple株のような長期的に伸びている株でやって最終資産額を見てもあまり意味がない気がするので，もう少し変化が小さい株でやるか，他の指標を最大化する必要がありますね…

まとめコード

#データ取得部分
import pandas_datareader.data as web
import datetime
start = datetime.date(2018,1,1)
end = datetime.date.today()
data = web.DataReader('AAPL', 'yahoo', start, end) #データの取得


#バックテスト部分
from backtesting import Backtest, Strategy # バックテスト
from backtesting.lib import crossover
from backtesting.test import SMA # SMAインジケータ

def backtesting(x1, x2):

    print('x1 :', x1, 'x2 :', x2)

    class SmaCross(Strategy):
        n1 = int(x1) # 短期SMA
        n2 = int(x2) # 長期SMA

        def init(self):
            self.sma1 = self.I(SMA, self.data.Close, self.n1) 
            self.sma2 = self.I(SMA, self.data.Close, self.n2)

        def next(self): #チャートデータの行ごとに呼び出される
            if crossover(self.sma1, self.sma2): #sma1がsma2を上回った時
                self.buy() # 買い
            elif crossover(self.sma2, self.sma1):
                self.position.close() # 売り

    # バックテストの設定
    bt = Backtest(
        data, # チャートデータ
        SmaCross, # 売買戦略
        cash=1000, # 最初の所持金
        commission=0.00495, # 取引手数料
        margin=1.0, # レバレッジ倍率の逆数（0.5で2倍レバレッジ）
        trade_on_close=True, # True：現在の終値で取引，False：次の時間の始値で取引
        exclusive_orders=True #自動でポジションをクローズ
    )

    output = bt.run() # バックテスト実行
    score = output['Equity Final [$]']

    print('Equity :', score)

    return score


#ベイズ最適化部分
from bayes_opt import BayesianOptimization

x1_max, x1_min = 50, 10
x2_max, x2_min = 50, 10

# 探索するパラメータと範囲を決める
pbounds = {'x1': (x1_min, x1_max), 'x2': (x2_min, x2_max), }

# 探索対象の関数と、探索するパラメータと範囲を渡す
bo = BayesianOptimization(f=backtesting, pbounds=pbounds)
# 最大化する
bo.maximize(init_points=10, n_iter=90)

print('OPTIMIZE: END')


#グラフ描画部分
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

def plot_bo(bo):
    # プロット範囲
    X1 = [x1 for x1 in np.arange(x1_min, x1_max, 0.1)]
    X2 = [x2 for x2 in np.arange(x1_min, x2_max, 0.1)]
    X1, X2 = np.meshgrid(X1, X2)

    # サンプル点
    xs1 = [bo.res[p]['params']['x1'] for p in range(len(bo.res))]
    xs2 = [bo.res[p]['params']['x2'] for p in range(len(bo.res))]
    ys = [bo.res[p]['target'] for p in range(len(bo.res))]
    ax.scatter(xs1,xs2, ys, c='black', s=20, zorder=10, label='sample')

    # 最大値
    print(bo.max)
    max_x1 = bo.max['params']['x1']
    max_x2 = bo.max['params']['x2']
    max_y = bo.max['target']
    print('max = ', max_x1, max_x2, max_y)
    for y in range(0, int(max_y)): #stick
        ax.scatter([max_x1],[max_x2], y , c='green', s=1)
    ax.scatter([max_x1],[max_x2],[max_y], c='green', s=100, zorder=10, label='pred_max')

# 結果をグラフに描画する
plot_bo(bo)
# グラフを表示する
plt.legend()
plt.grid()
plt.show()

投資に関する免責事項
本記事はプログラムや考え方の情報の提供・作業代行を目的としており，投資勧誘を目的とするものではありません．また，この記事は投資成績を保証するものではありません．投資はあくまで自己責任でお願いします．