Twitter分析大好きなFooQooです.暇さえあればTwitterで情報収拾してます.
本記事は「Twitterユーザの分析はブラウザだけでもできる (SocialDog + Colaboratory)」の続編となります.
Twitterユーザの特徴分析
近年Twitterマーケティングが盛んに行われており,獲得したフォロワーを潜在的な顧客としたプロモーション活動が行われています.
そのような場合において,各ユーザの性質を分析することによって,性質に特化したプロモーションの戦略を打つことができるようになります.
そこで本記事では,主成分分析を利用して,ユーザを特徴づける性質の定量化を行い,その性質がユーザのどのような振る舞いを説明しているか考察を行いました.
Twitterユーザの特徴量について
前回の記事では,SocialDogを用いてTwitterユーザのデータに含まれる以下の統計量を特徴量としました.
- フォロワー数
- フォロー数
- FF比 (フォロワー数/フォロー数)
- お気に入りした回数
- ユーザがリストに追加された数
- ユーザが投稿したツイート数
本記事では,引き続き以上の統計量を元にユーザの性質を分析します.
また分析するデータは,前回と同様,プロフィールに「パズドラ」が含まれるユーザデータを使用しました.
ユーザ特徴の仮説
実際の分析に入る前に,先ほど挙げた特徴量同士の関連性について確認し,ユーザ特徴の仮説を建てました.
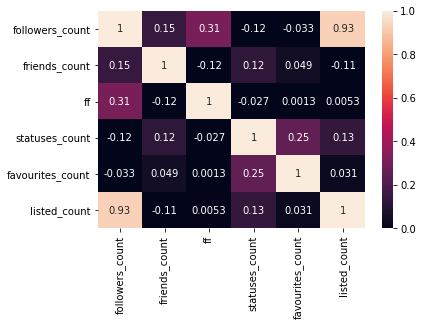
はじめに,特徴量同士の関連性について確認するため,特徴量間の偏相関係数を求めました.
偏相関係数とは,対象となる変量の組み合わせ以外の影響を取り除いて計算された相関の強さを表す値です.
純粋な2変量の相関の強さを計算することができるため,特定の変量に対する相関の強さを変量ごとに比較することができるようになります.
偏相関係数は以下のpythonコードにより計算を行いました.
途中の行列の演算では,対角成分が$-1$になってしまうので,これが$1$になるよう調整を行なっています.
# 偏相関行列の計算
def partial_corr(mat):
coef_inv = np.linalg.inv(mat)
D = np.diag(np.power(np.diag(coef_inv ),-0.5))
mat = -np.dot(np.dot(D,coef_inv),D)
return mat + 2*np.eye(mat.shape[0])
参考:分散共分散行列を相関行列/偏相関行列に変換 (Python)
この結果に対する考察を考えてみましょう.
まずフォロワー数とリストに追加された数に強い正の相関がみられます.
この特徴量は,他のユーザが当該ユーザに魅力を感じることによって増加する特徴量です.
したがって,ユーザの特徴の一つに,人気度があると考えられます.
次に,ツイート数とお気に入り数に弱い正の相関があります.
この特徴量は,当該ユーザがTwitterのサービスを頻繁に利用することによって増加します.
したがって,Twitter利用頻度がユーザ特徴の一つにあると考えられます.
以上の考察により,Twitterユーザには以下の潜在的な特徴があり,この特徴が対応する特徴量に影響を与えているという仮説を得ました.
- ユーザの人気度
- ユーザのTwitter利用頻度
主成分分析によって仮説を検証する
主成分分析について
主成分分析とは,データを主要な変動に要約して特徴を把握するための統計的手法です.
説明変量が$p$個存在する時,これらの変量が説明する主要な変動 $z$ を説明する関数を以下の一次結合で示す
$$z=l_1 x_1 + l_2 x_2 + \cdots + l_p x_p$$
を仮定し,$\sum_{i=1}^{p} {l_{i}}^2 = 1$の条件下で $z$ の分散が最大になる時の $z$ を第1主成分 と呼び,$z_1$とします.
次に $z_1$ と無関係な $z$ のうち$\sum_{i=1}^{p} {l_{i}}^2 = 1$の条件を満たす最大の分散を持つ $z_2$ を第2主成分を決定します.
この計算を繰り返し,全変動の大部分が $z$ によって説明されれば,主成分の計算を終了します.
主成分分析は,scikit-learnによって簡単に実行できます.
# 主成分分析
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
## 前処理: 標準化
ss = StandardScaler()
ss_data = ss.fit_transform(data)
# 実行
pca = PCA(n_components=max_components)
pca.fit(ss_data)
寄与率と因子負荷量
主成分が元のデータをどの程度説明できるのか知る目安として,寄与率があります.
これは,p変量の主成分 $z_{\alpha}$ の分散における,それぞれの主成分の分散の総和に対する割合を計算することによって求められます.
また,各主成分 $z_{\alpha}$ と変量 $x_j$ の相関係数を主成分 $z_{\alpha}$ の因子負荷量 と呼びます.
寄与率および因子負荷量は以下のpythonコードによって求めることができます.
# 寄与率
propotion = pca.explained_variance_ratio_
# 因子負荷量
loading = (pca.components_.T * np.sqrt(pca.explained_variance_)).T
実験
先ほど分析を行なったデータに対して,主成分分析を行い,寄与率と因子負荷量を計算しました.
少々見辛いですが,以下の表にその結果を示します.
表中の因子負荷量は,その主成分における各変量の因子負荷量を示しており,この値が1に近い時正の相関が強く,0に近いほど相関が弱く,-1に近いほど負の相関が強くなります.
各主成分に対して以下の考察を行いました.
| 主成分 | 因子負荷量に対する考察 |
|---|---|
| 第1主成分 | フォロワー数・FF比・リストに追加された数が高く,ユーザの人気度を表すと考えられる |
| 第2主成分 | ツイート数・お気に入り数が高く,ついでフォロー数がやや高い,ユーザのTwitter利用頻度を表すと考えられる |
| 第3主成分 | フォロー数が高いが,お気に入り数ついでツイート数が負方向にやや高い,無差別フォローのみ行うアカウント(Botや業者等)の性質を表すと考えられる |
| 第4主成分 | ツイート数がやや高いが,お気に入り数が負方向にやや高い,それぞれのサービスを特に利用する性質の主成分だと考えられる |
| 第5主成分 | FF比がやや高い,一定のFF比を持つユーザの性質を表すと考えられる |
第1主成分,第2主成分ともに先ほど建てた仮説を裏付けるような結果となりました.
また寄与率で比較した場合,ユーザの人気度の方がTwitter利用頻度よりも大きくユーザの性質に影響を与えていることがわかります.
また第4主成分は,正方向に主成分が高い時にツイート投稿の頻度が高いユーザを表し,負方向に主成分が高い時にお気に入りの登録頻度が高いユーザを表していると考えられます.
まとめ
Twitterユーザの統計量を主成分分析して,Twitterユーザの性質の分析を行いました.
この実験によって得られた主成分をその主成分が表すユーザの性質のスコアとして扱うことによって,それぞれの性質が高いユーザを抽出し,ユーザに合わせたプロモーションを打つことができると考えられます.
機会があれば,スコア化したユーザの確認を行い,先ほど考察した性質が反映されているか確認を行いたいと思います.