目的
レイマーチを試したのでその備忘録
固定長進行レイマーチングやってみた
本記事はこのサイトにあるコードをちょっといじったものになります
やること
Unityでレイマーチングのシェーダーを書いて z = f(x,y) の形の関数を表示させる
レイマーチングとは
光の経路を逆算して描画する方法
詳しくは他の記事参照
今回は本来のレイマーチングとは違って固定長でレイを進める
実装
球を表示する
Shader "Custom/RayMarching/Sphere"
{
Properties
{
_Threshold("Threshold", Range(0.0,3.0)) = 0.6 // 閾値
_Color("Color", Color) = (1.0,1.0,1.0,1.0) // 表面の色
}
SubShader
{
Tags{ "Queue" = "Transparent" }
LOD 100
Pass
{
ZWrite On
Blend SrcAlpha OneMinusSrcAlpha
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 pos : POSITION1;
float4 vertex : SV_POSITION;
};
// vert関数は本題ではないので簡潔に
v2f vert(appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.pos = mul(unity_ObjectToWorld, v.vertex);
o.uv = v.uv;
return o;
}
float _Threshold;
fixed4 _Color;
// 今の位置が球の内部かどうか
bool IsInObject(float3 pos)
{
return distance(pos, float3(0.0, 0.0, 0.0)) < _Threshold;
}
// ライティング(Lambert)
float LightingObject(float3 pos)
{
return saturate(dot(normalize(pos),_WorldSpaceLightPos0));
}
fixed4 frag(v2f i) : SV_Target
{
fixed4 col;
// 背景は透明に
col.xyz = 0.0;
col.w = 0.0;
// レイの初期位置(表面上)
float3 pos = i.pos.xyz;
// レイの進行方向
float3 forward = normalize(pos.xyz - _WorldSpaceCameraPos);
// 一定の割合でレイが進行
// オブジェクト内に到達したら光の計算
// 当たらなかったら色変更なし(透過)
const int StepNum = 2000;
const float MarchingDist = 0.03;
for (int i = 0; i < StepNum; i++)
{
if (IsInObject(pos))
{
col.xyz = _Color.xyz * LightingObject(pos);
col.w = 1.0;
break;
}
pos.xyz += MarchingDist * forward.xyz;
}
return col;
}
ENDCG
}
}
}
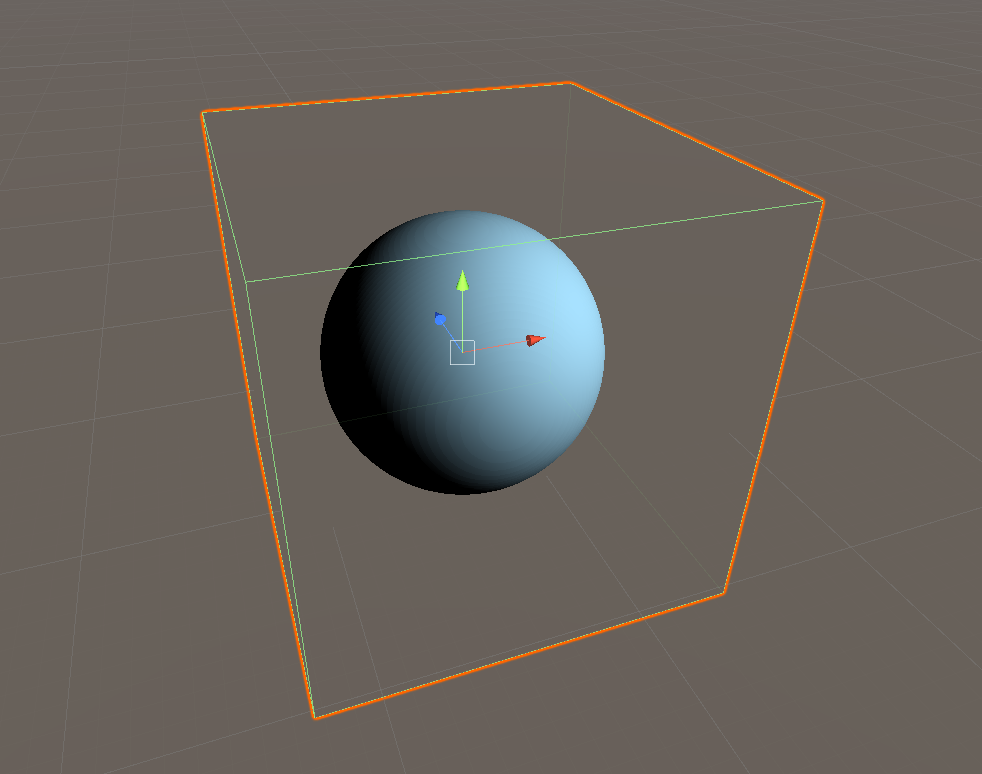
単純に球を表示するだけです
_Thresholdで球の半径を
_Colorで球の色を指定できます
画像では色を空色っぽく変更しています
// ライティング(Lambert)
float LightingObject(float3 pos)
{
return saturate(dot(normalize(pos),_WorldSpaceLightPos0));
}
球の表面の法線は球の中心から見た点方向のベクトルなので、それとワールドにある平行光線の方向の内積を取ることで陰を表現できます
詳しくは「Lambert反射」を調べてください
関数を表現する
Shader "Custom/RayMarching/Function"
{
Properties
{
_Threshold("Threshold", Range(0.0,3.0)) = 0.6
_Color("Color", Color) = (1.0,1.0,1.0,1.0)
_Ambient("Ambient", Color) = (0.0,0.0,0.0,0.0)
}
SubShader
{
Tags{ "Queue" = "Transparent" }
LOD 100
Pass
{
ZWrite On
Blend SrcAlpha OneMinusSrcAlpha
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 pos : POSITION1;
float4 vertex : SV_POSITION;
};
v2f vert(appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.pos = mul(unity_ObjectToWorld, v.vertex);
o.uv = v.uv;
return o;
}
float _Threshold;
fixed4 _Color;
fixed4 _Ambient;
float Func(float x, float z){
return sin(x) + sin(z);
}
float3 CalcNormal(float2 pos){
const float delta = 0.00001;
float x = pos.x;float z = pos.y;
float dx = Func(x + delta,z) - Func(x - delta, z);
float dz = Func(x, z + delta) - Func(x, z - delta);
dx /= delta;
dz /= delta;
return normalize(-float3(dx,-1,dz));
}
bool isInObject(float3 pos) {
return pos.y < Func(pos.x,pos.z);
}
float LightingObject(float3 pos){
return saturate(dot(CalcNormal(pos.xz),_WorldSpaceLightPos0));
}
fixed3 ColorDefine(float3 pos){
float lightRate = LightingObject(pos);
return _Color.xyz * lightRate + _Ambient * (1 - lightRate);
}
fixed4 frag(v2f i) : SV_Target
{
fixed4 col;
col.xyz = 0.0;
col.w = 0.0;
float3 pos = i.pos.xyz;
float3 forward = normalize(pos.xyz - _WorldSpaceCameraPos);
const int StepNum = 2000;
const float MarchingDist = 0.03;
for (int i = 0; i < StepNum; i++) {
if (isInObject(pos)) {
col.xyz = ColorDefine(pos);
col.w = 1.0;
break;
}
pos.xyz += MarchingDist * forward.xyz;
}
return col;
}
ENDCG
}
}
}
関数では球ほど簡単には法線を計算できないので、それ専用の関数を作っています
float3 CalcNormal(float2 pos){
const float delta = 0.00001;
float x = pos.x;float z = pos.y;
float dx = Func(x + delta,z) - Func(x - delta, z);
float dz = Func(x, z + delta) - Func(x, z - delta);
dx /= delta;
dz /= delta;
return normalize(-float3(dx,-1,dz));
}
関数
z=f(x,y)
の、点(a,b,f(a,b))での法線は
(f_{x}(a,b),f_{y}(a,b),-1)
と表わされ、fx,fyはそれぞれdx,dyに対応しているわけです
ただしここで2点注意しなければいけないことがあって
一つはUnityはy軸が上方向なので式中のyとzを入れ替えなければならないこと
二つ目は実際の法線は逆方向なので-1をかけなければならないこと
それを考慮すると上記の関数ができます
Func関数の中身をいじれば別の関数を表示することもできます
まとめ
レイマーチングだと関数を正確に表現できるのでどこかで使えそう(適当)
関数次第でどんな図形も表現できるのは素晴らしいと思います