Pythonではじめる機械学習 決定木

#はじめに
"Pythonではじめる機械学習"の決定木(p70~82)の学習記録です。
・分からなかったコードやドキュメント
・自分にとって理解するのに時間がかかった内容
・用語の定義
に関する説明を主に記述しています。
参考書を読んでいて容易に理解できたことは記述していません。

#2.3.5　決定木
決定木はクラス分類と回帰タスクに広く用いられている。
Yes/Noで答えられる質問で構成された階層的な木構造を学習する。

##2.3.5.1　決定木の構築
決定木における学習は、正解にたどり着けるような一連のYes/No型の質問の学習を意味する。
これらの質問はテスト(test)と呼ばれる。モデルの汎化性能を測るためのテストセットとは違う。
通常のデータの特徴量は連続値になっており、連続値に対するテストは「特徴量 i は値 a よりも大きいか？」という形をとる。

##2.3.5.2　決定木の複雑さの制御
葉が純粋(1つの対象値のデータポイントしか含まないような決定木の葉)になるまで分割を続けると、モデルが複雑になりすぎ訓練データに対して大幅に過剰適合してしまう。
それらを解消するために事前枝刈り(pre-pruning)と事後枝刈り(post-pruning)がある。
"事前枝刈り"は木の深さを制限する方法、歯の最大値を制限する方法、分割する際にその中に含まれている点の最小数を決めておく方法などで木の生成を早めに止める。
"事後枝刈り"は情報の少ないノードを削除する。

疑問
・内部でタイブレークに使われるrandom_stateってどういう意味？

##2.3.5.3　決定木の解析
treeモジュールのexport_graphviz関数を使って木を可視化することができる。
graphvizの引数についてhttps://future-chem.com/ames-decision-tree/#graphviz
with openは

In[58]:  # 木の構成を設定
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant", "benigh"], feature_names=cancer.feature_names, impurity=False, filled=True)

In[59]:  # 木の可視化
import graphviz
with open("tree.dot")as f:
    dot_graph = f.read()
graphviz.Source(dot_graph)

疑問
・dotファイル形式って何？
https://wa3.i-3-i.info/word17856.html
・with構文
https://techacademy.jp/magazine/15823

##2.3.5.4　決定木の特徴量の重要性
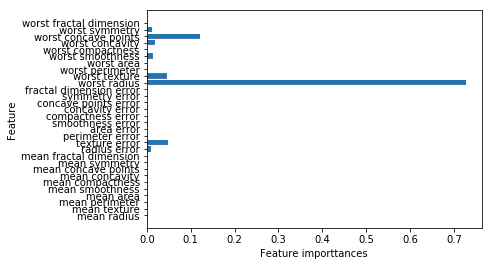
決定木の挙動を要約するのによく使われるのが特徴量の重要度(feature importance)である。
特徴量の重要度の和は1になる。

決定木による回帰も行うことができる。
しかし，決定木による回帰では外挿(訓練データの範囲の外側に対しての予測）ができない。
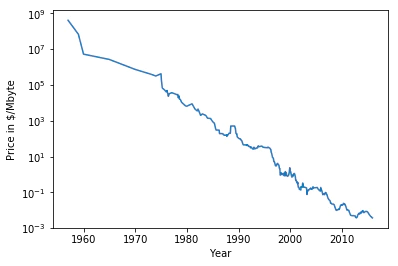
計算機のメモリ(RAM)価格の履歴データを用いてこの例を見てみる。

In[63]:
import pandas as pd
import os

# pd.read_csvでcsvファイルを読み込む os.path.joinでパスとファイル名を結合し，1つのパスを返す
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))

# y軸を対数スケールする
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")

Out[63]:

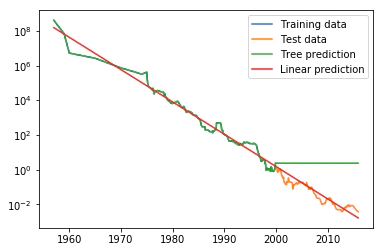
以上のデータを用いて決定木モデルと線形回帰モデルによる予測をする。

In[64]:
from sklearn.tree import DecisionTreeRegressor

data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]

# 日付に基づいて価格を予測
X_train = data_train.date[:, np.newaxis]
# 対数変換
y_train = np.log(data_train.price)

# モデルに訓練セットを学習させる
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)

# 全ての価格を予想
X_all = ram_prices.date[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)

# 対数変換をキャンセルするため逆変換
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)


Im[65]:
plt.semilogy(data_train.date, data_train.price, label="Training data")
plt.semilogy(data_test.date, data_test.price, label="Test data")
plt.semilogy(ram_prices.date, price_tree, label="Tree prediction")
plt.semilogy(ram_prices.date, price_lr, label="Linear prediction")
plt.legend()

Out[64, 65]:

線形モデル(データを直線で近似する)は訓練データとテストデータの双方において細かい変異を取りこぼしているものの、テストデータ(2000年以降のデータ)に対してかなり良い予測を与えている。
一方、決定木のほうは、複雑さを制御していなのでデータセットを完璧に覚えているため、訓練データに対して完璧な予測を行う。
しかし、モデルがデータを持っていない領域になると、決定木は知っている最後の点を返してくるだけになる。

疑問
・import osの意味
https://www.sejuku.net/blog/63651
・csvファイルって何？
https://www.sejuku.net/blog/63651
・np.newaxisとは？
https://qiita.com/rtok/items/10f803a226892a760d75

##2.3.5.5　長所、短所、パラメータ
決定木は他のアルゴリズムと比較して、2つの長所がある。
・結果のモデルが容易に可視化可能で、専門家でなくても理解可能であること
・データのスケールに対して完全に不変であること
決定木の最大の問題点は、事前刈りを行ったとしても過剰適合しやすく、汎化性能が低い傾向があることである。ほとんどのアプリケーションにおいては、決定木を単体で使うのではなく、アンサンブル法が用いられる。

疑問
・「個々の特徴量は独立に処理され、データの分割はスケールに依存しないので、決定木においては特徴量の正規化や標準化は必要ないのだ」