はじめに
Pythonは機械学習の研究などで多く用いられているプログラミング言語です。特に基礎研究の分野でも使いたいという場合には、これがかえって使いにくくなってしまうことがよくあります。なぜなら、for文を多く書くと遅くなるからです。そこで、for文を書かずに頑張ろうとすると色々なトラブルに出くわすのですが、その中でも筆者が手こずったnp.newaxisの使い方を紹介していこうと思います。これは、いろんなパラメータで実験したいときなどに多く出くわすでしょう。
※スライスについて事前知識があるものとして説明します。調べるなどして事前に知識を入れておいてください。
[Python]Numpyの参照、抽出、結合
Indexing - docs.scipy.org
本編
1. まず用いるデータを把握しましょう
はじめは、どんなデータがあって、どんなゴールへ向かわせたいのかをしっかり整理するとよいです。
どんなデータで、配列の形状はどうなっているか、何次元なのかをしっかり頭に入れておきましょう。
簡単のために次のような状況を考えてみます。
import numpy as np
assert a.shape == (N,) # ndarray
assert b.shape == (N, K) # ndarray
-
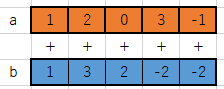
a、bは共にベクトルで、a+bをしたい
-
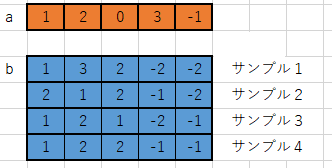
bはK個のサンプルを持っているので実体は(N, K)の二次元配列で格納している
これをfor文でかくと、
c = np.zeros(N, K)
for k in range(K):
c[:, k] = a + b[:, k]
ですが、for文はできるだけ書きたくありません。
また、a+bと単純にやってもできますが、これでは複雑な問題のときに全く対応できなくなります。
2. ゴールを考える。
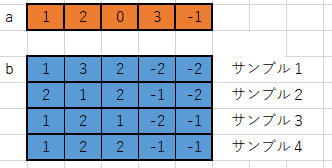
今回のゴールは、K個のbのサンプルごとにa+bを行い、サンプルごとの結果を得たいわけです。最終的に得たい結果=(ゴールの配列)の形状をしっかりと定義しましょう。
c = np.zeros(N, K)
hogehoge()
assert c.shape == (N, K)
こうなります。
3. np.newaxisの挿入
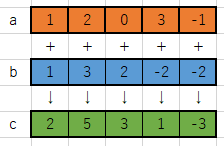
普通にa+bを頭の中でするとこうなるのですが、
bには複数のサンプルがある2次元配列なのでどう計算していいのかわかりません。
※実際は自動的に推測してくれますが、これに任せきるのは今後よくありません。
これを、どう計算するべきかの指示をこちらで与えてあげましょう。それがnp.newaxisです。
実は、np.newaxisの実体はNoneですが、あまり気にせずnp.newaxisを使いましょう。
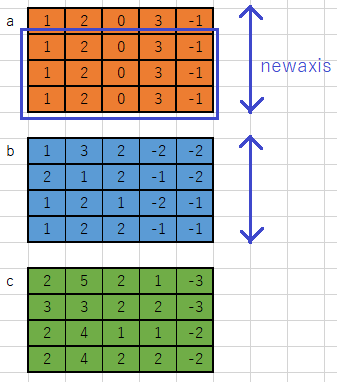
配列が同じ形状であることを必要とする演算(ここでは+)が来たとき、こちらから「同じ形状にしてください」という指示をします。まず、配列の次元がa.shape == (N,)なので、せめてa.shape == (N, 1)にしてあげます。そのために、a[:, np.newaxis]とします。この操作によって、Numpyが自動的に演算子のもう片方の引数から判断できるようになり、(N, 1)から(N, K)に引き伸ばして計算を行ってくれます。
import numpy as np
assert a.shape == (N,) # ndarray
assert b.shape == (N, K) # ndarray
# a[:, (ここが足りてない)]
c = a[:, np.newaxis] + b[:, :]
assert c.shape == (N, K) #エラーチェックとメモの役割を同時に持たせましょう
まとめ
このように、Numpyが自動的にやってくれる処理を冷静に理解してみると、複雑な問題にも簡単に対応できるようになります。
※もっと難しい問題の場合もあとで追記します。
※説明がわかりにくいなと感じることがあれば、ぜひ教えてください。質問などもコメントにて受け付けます。