この記事で学べる事
ブラシレスモータを自分で制御する方法がわかります。
方位磁針を回すには?
あるところにコンパスがありました。
このコンパスを見て、あなたは「このコンパスを正方向(反時計回り)に回したいなぁ...。」と思いました。そのためには、とりあえず、コンパスの周辺にいい感じの向きの磁界を発生させればよさそうですよね。
では、どのような向きの磁界を発生させれば一番効率よく回せるのでしょうか。
例えば以下のような配置で磁石(モノポールみたいなのは許してください)を置いた場合には、コンパスはNとSが引き合い、常にこの向きをキープしようとしますよね。
逆に、以下のように磁石の配置を180°反転させた場合は、反発しあいますが、どちら向きに回転するかわからないですし、あまり回転方向に力は発生しなさそうですよね。
以上のことを踏まえると、磁石の配置を最初の状態(引き合うときの配置)から、正方向に90°回した以下のような配置が一番よさそうだということは、なんとなくわかりますよね。
この図を見ると、磁石同士の引き合いと反発の力が、すべて同じ大きさでいい感じの向きに働くのがわかります。
では、コンパスを常に回し続けるにはどうすればよいでしょうか。
これは簡単なことで、以下の図のようにコンパスの針の向きに対して常に正方向に90°回した磁界を発生させればよいだけです。
つまり、コンパスの向きに対する相対的な磁界の向きが90°になるように制御すればよいです。コンパスの向き向きに対する相対的な座標系をdq座標系といい、以下のように表されます。(コンパスの土台(正方形)が逆回転しているように見えるが、実際はコンパスの針が正回転している。)
これに対して、コンパスの土台を基準にした絶対的な座標系をαβ座標系といい、以下のように表されます。
dq座標系からαβ座標系への変換は簡単で、コンパスの角度の回転行列をかけるだけです。コンパスの角度を$\theta$とおくと
\begin{pmatrix} \alpha \\ \beta \end{pmatrix}
=
\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}
\begin{pmatrix} d \\ q \end{pmatrix}
その逆変換も簡単で、逆回転行列をかけるだけです。
\begin{pmatrix} d \\ q \end{pmatrix}
=
\begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix}
\begin{pmatrix} \alpha \\ \beta \end{pmatrix}
3相コイルで回転磁界を作ろう
あるところにコイルがありました。
電流を右に流してみたところ、磁界も右向きに発生しました。(磁界は電流に比例する法則があります。)
この場合、磁界と電流のベクトルは同一視することができます。
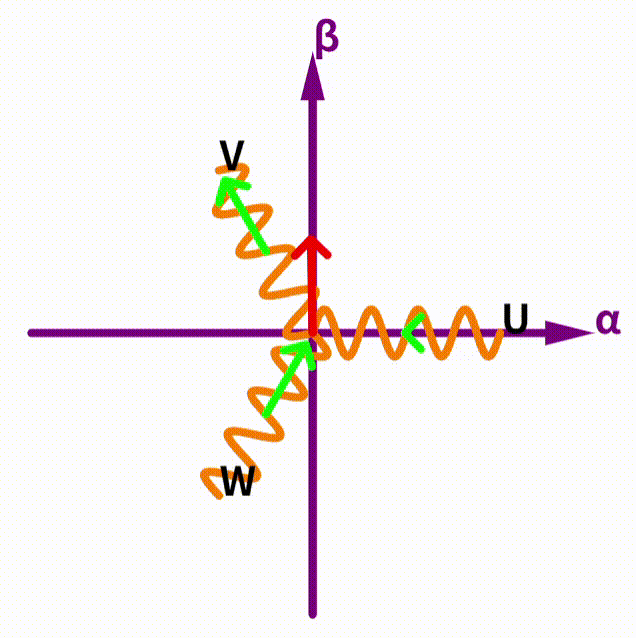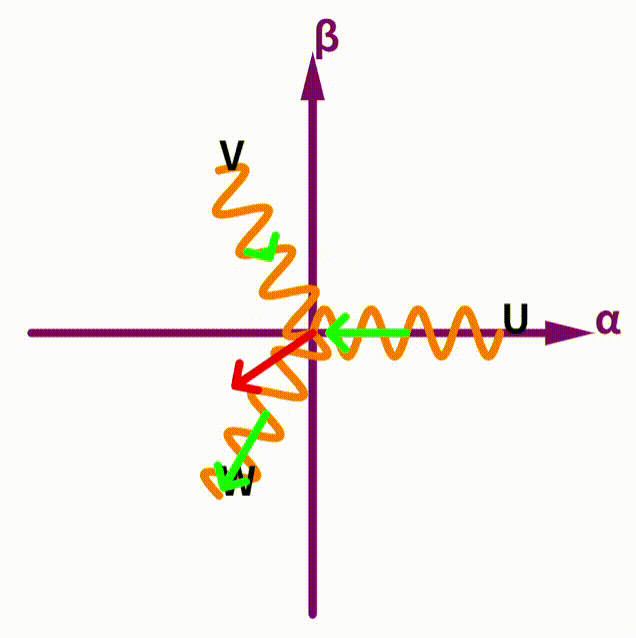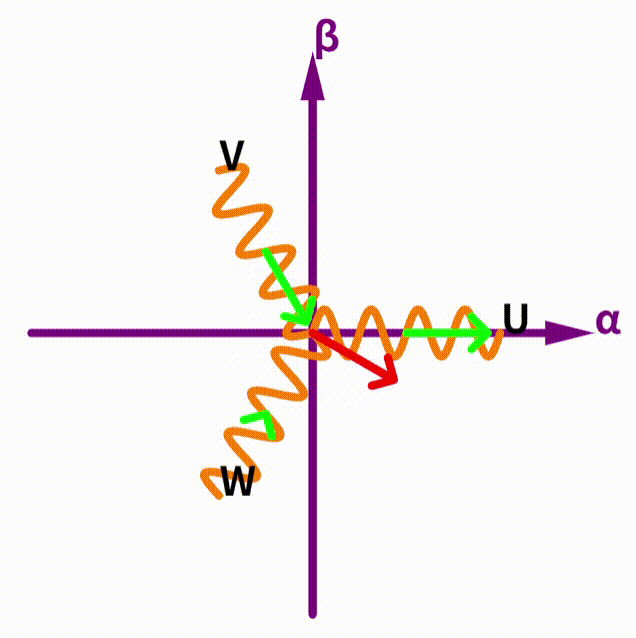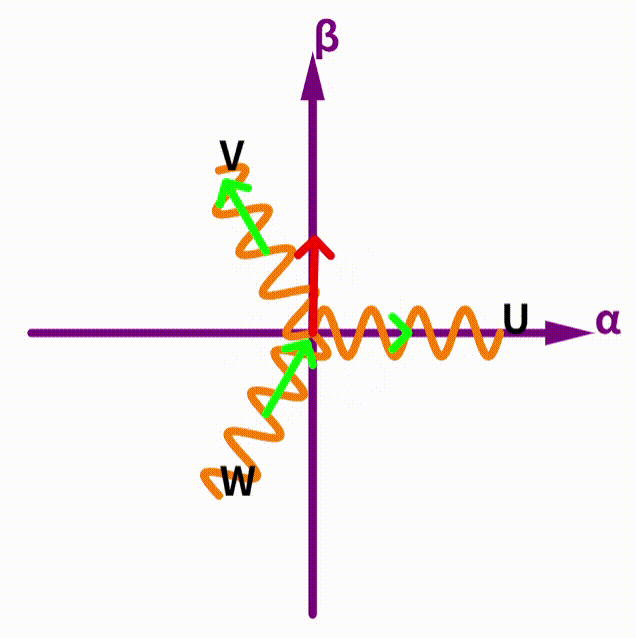
では、以下のように3つのコイルが配置されていて、以下のように電流が流れていたとします。(Uに1[A]、Vに-0.5[A]、Wに-0.5[A])
この場合、全体としてどのような磁界が発生するでしょうか。
この場合、各コイルで発生する磁界のベクトルは、各コイルの電流ベクトルと同一視できるので、全体の磁界はこの3つのベクトルを合成したものになります。よって、右向きの磁界になります。
では、これらの関係を式にしていきたいと思いますが、ここで、αβ座標系を使います。先ほどαβ座標系は固定された絶対的な座標系だと説明しました。ブラシレスモータにおいてコイルはステータ側であり、固定されているので、αβ座標系座標系でコイルの位置は固定です。
まず、U、V、W各コイルの固有ベクトル(大きさは1で、コイルの向きを表すベクトル)を定義します。
\vec{u}=\begin{pmatrix} 1 \\ 0 \end{pmatrix},\,
\vec{v}=\begin{pmatrix} -\frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{pmatrix},\,
\vec{w}=\begin{pmatrix} -\frac{1}{2} \\ -\frac{\sqrt{3}}{2} \end{pmatrix}
このベクトルの定義の仕方は簡単で、以下の図を見れば、すぐ納得できると思います。
本当にコイルの向きをそのままベクトルにしただけです。
各コイルの電流を$I_{u},\,I_{v},\,I_{w}$とすると、磁界のベクトルは
I_{u}\cdot\vec{u}+I_{v}\cdot\vec{v}+I_{w}\cdot\vec{w}
で表せそうですよね。電流と磁界のベクトルは同一視できるので、全体の電流ベクトルをαβ座標系で定義したい場合も上の式で表せそうですが、Uに1[A]、Vに-0.5[A]、Wに-0.5[A]流した際の電流ベクトルを$\begin{pmatrix} 1 \\ 0 \end{pmatrix}$と定義したいので、前に係数として2/3をかけます。
よって、αβ座標系での電流ベクトルは、
\vec{I_{\alpha\beta}}=\frac{2}{3}(I_{u}\cdot\vec{u}+I_{v}\cdot\vec{v}+I_{w}\cdot\vec{w})
となります。
ここまで、電流ベクトルを例に挙げてきましたが、電圧も同様にベクトルで表すことができます。
次に、αβ座標系からUVWへの変換です。先ほどのものの逆変換です。ここでは、電圧を例に説明します。今までの計算や、上のアニメーションを見て気づいた勘の良い人もいるかもしれませんが、αβ座標系での電圧ベクトルと、UVWの各単位ベクトルとの内積が、UVWの各出力電圧(端子電圧)となります。具体的な式を以下に示します。
V_{u}=\vec{V_{\alpha\beta}}\cdot\vec{u},\,
V_{v}=\vec{V_{\alpha\beta}}\cdot\vec{v},\,
V_{w}=\vec{V_{\alpha\beta}}\cdot\vec{w}
この式を見て、改めて上のアニメーションを見ると、確かになんとなく内積になっていそう(ベクトルがそれぞれのコイルの方向成分の射影として分解されていそう)ですよね。
式のまとめ
一回今までの式を整理しましょう。データの変数名は$x$とします。
\vec{u}=\begin{pmatrix} 1 \\ 0 \end{pmatrix},\,
\vec{v}=\begin{pmatrix} -\frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{pmatrix},\,
\vec{w}=\begin{pmatrix} -\frac{1}{2} \\ -\frac{\sqrt{3}}{2} \end{pmatrix}
- UVWからdq
\vec{x_{\alpha\beta}}=\frac{2}{3}(x_{u}\cdot\vec{u}+x_{v}\cdot\vec{v}+x_{w}\cdot\vec{w})
\vec{x_{dq}}
=
\begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix}
\vec{x_{\alpha\beta}}
- dqからUVW
\vec{x_{\alpha\beta}}
=
\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}
\vec{x_{dq}}
x_{u}=\vec{x_{\alpha\beta}}\cdot\vec{u},\,
x_{v}=\vec{x_{\alpha\beta}}\cdot\vec{v},\,
x_{w}=\vec{x_{\alpha\beta}}\cdot\vec{w}
適当にブラシレスモータを回してみよう(強制転流)
この辺から難しくなるかもしれないので、ChatGPTと協力したほうがいいかもしれないです。
まず、エンコーダを使わずにブラシレスを回す方法(強制転流)です。
ここまで、UVWの電圧を扱ってきましたが、これはPWMのDuty比に相当します。ただ、これでは負の電圧を扱うことができません。そのため、Duty比=50%のときを基準電圧で$V=0$[V]とし、そこからPWMを±50%の範囲で動かすことによりモータを制御します。
Duty=0.50+0.50\cdot V
この式で、Vが-1.0~+1.0のときにDuty比が0%~100%になります。
ただ、実際には電流を読んだり、ゲート駆動とか色々な安全のために最大のDuty比を抑えるために
Duty=0.50+0.40\cdot V
とかにします。
適当にブラシレスモータを回すには、$t$[s]を時間とすると、
\theta=2\pi t
\vec{V_{\alpha\beta}}=0.01\cdot\begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix}
V_{u}=\vec{V_{\alpha\beta}}\cdot\vec{u},\,
V_{v}=\vec{V_{\alpha\beta}}\cdot\vec{v},\,
V_{w}=\vec{V_{\alpha\beta}}\cdot\vec{w}
Duty_{u}=0.50+0.40\cdot V_{u},\,
Duty_{v}=0.50+0.40\cdot V_{v},\,
Duty_{w}=0.50+0.40\cdot V_{w},\
これで回すと、ゆっくりブラシレスモータが回ります。回らないなら、おそらく出力が足りないので、二段目の式の係数の0.01を、少しずつ上げてみましょう。
実際のブラシレスモータに式を適用しよう
まず、実際のブラシレスモータは、ステータのコイルが3つだけではないし、ロータの磁石は2つだけではありません。磁石は基本的にNとSが交互に並べられています(もしかしたらハルバッハとかになっているのもあるかもしれないが、実際に見たことはない)。磁石の数を極数(ポール数、Number of poles)といい、極数/2を対極数(Number of pole pairs)といいます。
コイルの数は対極数x3だとわかりやすいのですが、実際は違ったりします。ただ、計算の際はコイルの数は気にする必要はなく、対極数だけで考えればよいです。
よくある構成は、
磁石の数 : 14
コイルの数 : 12
対極数 : 7
です。4250や、5010、RoboMasterのM2006等の小型~中型モータは、すべて確かこの構成です。
このとき、対極数は、3相交流を何周期モータに流せば一回転するのか、というのに一致します。対極数を簡単に確かめるには、ブラシレスモータのUVWからどれか2端子を適当に選んで、電流制限を0.5[A]くらいに設定した安定化電源の+と-につないで、手で回してみてください(長時間はやめましょう)。すると、回すのに抵抗を感じると思います。一回転させる間に、ロータの吸い付く角度が何個かあると思いますが、その個数が対極数です。
先ほど、対極数は3相交流を何周期モータに流せば一回転するのか、というのに一致すると言いました。ベクトル制御で扱う角度($\theta_{e}$、ここまでの式では$\theta$、これを電気角という)は、モータの実際の角度($\theta_{m}$、エンコーダで取得、これを機械角という)に対極数をかければよいだけです。例えば、対極数が7のモータでは、
\theta_{e}=7(\theta_{m} - \theta_{offset})
となります。機械角が1周すると電気角が7周します。
ここで、上の式には気になるのがいますよね。そうです。$\theta_{offset}$です。
$\theta_{offset}$を求めるのは簡単で、先ほどの強制転流で$\theta=0$に固定したとき(あるいは、電流制限0.5[A]くらいの電源装置の+にU、-にVとWを繋いだとき)の機械角$\theta_{m}$(エンコーダの値)が$\theta_{offset}$です。これにより、エンコーダと電気角の0°が合います。
あと、エンコーダを扱う際にもう一つ注意点があります。回転の向きです。先ほどの強制転流でモータを回した際に、エンコーダの値が増加していることを確かめてください。もし減少している場合は、エンコーダの角度の符号を反転させるか、ブラシレスモータの接続のUとWを入れ替えるかしてください。
ちょっといい感じにブラシレスモータを回そう
ブラシレスモータを回すには、ロータに対して90°進めた磁界を発生させればよいです。つまり、電気角$\theta_{e}$に対して90°進めた電流を流せばよいです。よって、例えば$I$[A]のトルクでブラシレスモータを回すには、
\vec{I_{dq}}
=I\cdot\begin{pmatrix} \cos\frac{\pi}{2} \\ \sin\frac{\pi}{2} \end{pmatrix}
=\begin{pmatrix} 0 \\ I \end{pmatrix}
つまり、dq電流のd成分を0[A]、q成分を$I$[A]にすればよいです。
ただ、一旦電流制御はなしで回してみましょう。電圧は低速では大体電流に比例するので、
\vec{V_{dq}}
=\begin{pmatrix} 0 \\ 0.05 \end{pmatrix}
\vec{V_{\alpha\beta}}
=
\begin{pmatrix} \cos\theta_e & -\sin\theta_e \\ \sin\theta_e & \cos\theta_e \end{pmatrix}
\vec{V_{dq}}
V_{u}=\vec{V_{\alpha\beta}}\cdot\vec{u},\,
V_{v}=\vec{V_{\alpha\beta}}\cdot\vec{v},\,
V_{w}=\vec{V_{\alpha\beta}}\cdot\vec{w}
で駆動すれば、割といい感じに回ります。回らない場合は出力が弱いので、一段目の式の0.05を少しづつ上げてみましょう。これをdq電圧一定での駆動と言ったりします。
完璧にブラシレスモータを回そう
電流制御をしましょう。dq電流をPI制御(PIDのDゲインが0バージョン)するだけです。Pゲインはかなり小さくないと危ないです。Pゲインは最初は0でもいいので、Iゲインを先に調整しましょう。Iは割と上げていってもあまり暴走はしませんが、I項の最大値を設定しないと危ないです。また、PIの入力値であるのエラー値の最大値を設定すると、I項が急激に増加するのを防いだりできるので、そういう工夫をするといいかもしれません。できれば20kHz以上の制御周期がいいです。また、高速域では電流のノイズが荒ぶって、ものすごい音がすることがあるので、電源を素早く消せるようにしましょう。この場合は、最大Duty比を小さくすることで、速度を抑えることができます。高速運転はあきらめてください。
- 完璧にブラシレスモータを回すときの制御フロー(数式)
\vec{u}=\begin{pmatrix} 1 \\ 0 \end{pmatrix},\,
\vec{v}=\begin{pmatrix} -\frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{pmatrix},\,
\vec{w}=\begin{pmatrix} -\frac{1}{2} \\ -\frac{\sqrt{3}}{2} \end{pmatrix}
\theta_{e}=N_{PolePairs}(\theta_{m} - \theta_{offset})
\vec{I_{\alpha\beta}}=\frac{2}{3}(I_{u}\cdot\vec{u}+I_{v}\cdot\vec{v}+I_{w}\cdot\vec{w})
\vec{I_{dq}}
=
\begin{pmatrix} \cos\theta_{e} & \sin\theta_{e} \\ -\sin\theta_{e} & \cos\theta_{e} \end{pmatrix}
\vec{I_{\alpha\beta}}
\vec{V_{dq}}
=\begin{pmatrix} PI(0-I_{d}) \\ PI(I_{target}-I_q) \end{pmatrix}
\vec{V_{\alpha\beta}}
=
\begin{pmatrix} \cos\theta_e & -\sin\theta_e \\ \sin\theta_e & \cos\theta_e \end{pmatrix}
\vec{V_{dq}}
V_{u}=\vec{V_{\alpha\beta}}\cdot\vec{u},\,
V_{v}=\vec{V_{\alpha\beta}}\cdot\vec{v},\,
V_{w}=\vec{V_{\alpha\beta}}\cdot\vec{w}
さいごに
ブラシレスモータは、ドライバを自作する技術力はブラシモータとあまり変わらない(ブラシモータのほうがノイズ大きくて難しいと回路班が言っていた。ESCは小型化することができるので、そういった意味では配線は難しいかも)のですが、制御が難しいイメージがあって、ハードルが高くなっています。この記事を読んで、ロボットエンジニアたちのモータの選択肢がより広がれば嬉しいです。