勾配降下法に関して、Python機械学習プログラミング 達人データサイエンティストによる理論と実践の2章を参考にしながら、まとめ・演習を行なった。
本書2章ではADALINEやパーセプトロンも扱った。これらは機械学習やニューラルネットワークの理解の基礎となるが、実務ではほとんど使われないため、ここでは割愛した。
勾配降下法とは
教師あり学習は、入力値($x_{i}$)に対する適切な重み($w_{i}$)を学習する作業と言える（厳密にはバイアス項も学ぶがここでは省略）。
$$
\mathbf{w} =
\begin{bmatrix}
w_1 \
... \
w_m
\end{bmatrix}
$$
$$
\mathbf{x} =
\begin{bmatrix}
x_1 \
... \
x_m
\end{bmatrix}
$$
ー回帰問題ー
$$
y = \sum_{i=0}^{m} w_{i}x_{i} = \mathbf{w}^{T}\mathbf{x}
$$
ー分類問題ー
$$
z = \sum_{i=0}^{m} w_{i}x_{i} = \mathbf{w}^{T}\mathbf{x}
$$
$$
\phi(z) =
\begin{cases}
1 & (z \geq 0) \\
-1 & (z < 0)
\end{cases}
$$
このような教師あり学習の学習過程において、目的関数（いわゆるコスト関数）を最適化する手法が勾配降下法である。
機械学習の学習とは、予測値と正値の差（損失）をゼロにするために、入力（$x_{j}$）に対する重み（$w_{j}$）を更新しながら、最適な重み（$w_{j}^*$）を学習する作業と考えても良い。
損失関数と目的関数の違い
よく損失関数と目的関数の違いについて混乱するので、ここでまとめておく。
| 用語 | 意味 | 例 |
|---|---|---|
| 損失関数 (Loss) | 1個のデータ点に対する誤差 | 1枚の写真を猫と間違えたときの誤差 |
| 目的関数 (Objective) | データ全体に対して最適化する対象 | すべての写真の誤差＋モデルの複雑さをまとめたもの |
例えば、教師あり学習では
全データに関する予測と正値の誤差の平均 → 目的関数
１つのデータに関する予測と正値の誤差 → 損失関数
・回帰問題の損失関数（平均二乗誤差）: $Loss_{\text{MSE}} = \frac{1}{N} \sum_{i=1}^{N} (y_{\text{true},i} - y_{\text{pred},i})^2$
・分類問題の損失関数（クロスエントロピー損失）: $Loss_{\text{CE}} = - \sum_{i=1}^{N} y_{\text{true},i} \log(y_{\text{pred},i})$
・回帰問題の目的関数（平均二乗誤差）:
$Objective_{\text{MSE}} = \frac{1}{N} \sum_{i=1}^{N} (y_{\text{true},i} - y_{\text{pred},i})^2 + \text{正則化項}$
*正則化：モデルの複雑さを制限することで、過学習を抑制する方法。L1正則化（Lasso）やL2正則化（Ridge）がある。
勾配降下法のプロセス
簡単に言うと、重みを更新しながらコスト関数の最小値まで勾配を下っていくイメージ。
$$
w := w + \Delta w
$$
$$
\Delta w = - \eta \nabla J(w)
$$
$\eta$は学習率、$\nabla J(w)$はコスト関数の勾配、すなわち重み（$w_{j}$）ごとの偏微分なので、以下のように書ける。
$$
\nabla J(w) = \frac{\partial J}{\partial w_{j}} = - \sum_{i} (y^{(i)} - \phi(z^{(i)}))x_{j}^{(i)}
$$
勾配降下法においては、学習率の設定がキーとなる。
学習率が大きすぎると発散する可能性があり、小さすぎると収束が遅くなったり、局所最小値から抜け出せないから。
学習率スケジューラー
この問題の解決として、学習率スケジューラーと呼ばれる手法がある。トレーニングの最初の段階では学習率を大きく設定して、トレーニングが進むにつれて学習率を小さくする手法。これにより、収束を安定させたり、局所最適化に陥るのを防ぐ。
主に以下の５つの方法がある。
| 手法 | 概要 | 特徴 |
|---|---|---|
| ステップ減衰（Step Decay） | 一定のエポックごとに学習率を減少させる方法 | - 固定のステップごとに学習率が減少 - 単純で実装が簡単 |
| 指数減衰（Exponential Decay） | 学習率を指数的に減少させる方法 | - トレーニングが進むにつれて学習率が急激に減少 |
| コサインアニーリング（Cosine Annealing） | 学習率をコサイン関数に従って周期的に変化させる方法 学習率は減少し、一定周期で増加する |
- 学習率が周期的に変動 - 局所的な最適解を避けるために有効 |
| ReduceLROnPlateau | 精度が一定のエポック数で改善しない場合に学習率を減少させる方法 | - 精度が改善しないときに学習率を調整 -トレーニングが停滞しているときに有効 動的に学習率を変更 |
| ワームアップ（Warm-up） | トレーニングの初期段階で学習率を小さくし、段階的に学習率を増加させる方法 | - 初期の学習率を小さく設定 - 徐々に学習率を増加させて安定した学習を促す |
ReduceLROnPlateauとステップ減衰はシンプルかつ汎用性が高いため、この２つがとりあえずファーストチョイス。
具体的なシチュエーションとしては、学習が停滞してきた場合には変化を加えたいのであればReduceLROnPlateauを選び、逆に学習を段階的に落ち着かせたい場合にはステップ減衰が適しているといえる。
損失関数の監視
実務上、トレーニングの各エポックごとに損失関数を記録し、監視する方法が推奨される。
・収束している場合: 損失関数の値が減少し続け、一定の最小値に収束する。
・収束していない場合: 損失関数が減少しない、または増加している場合、学習がうまくいっていない可能性がある。学習率を減少させるか、別の最適化手法（Adamオプティマイザやモメンタム法）を検討する。
勾配降下法の種類
| 手法 | 概要 | 特徴 |
|---|---|---|
| バッチ勾配降下法 | 訓練データ全体を使用して勾配を計算する最適化手法 | - 収束は安定しているが、計算コストが高い - 訓練データ全体を使うため、更新が遅くなることが多い |
| 確率的勾配降下法 (SGD) | 1つの訓練データを使って勾配を計算し、逐次的にパラメータを更新 | - 計算が高速であるが、収束過程で振動が生じる - オンライン学習に適している - ミニバッチに比べてノイズが多いため、収束が不安定になることがある |
| ミニバッチ勾配降下法 | 訓練データの一部（バッチ）を使って勾配を計算する手法 | - バッチ勾配降下法とSGDのバランス - 計算の効率性と収束の安定性の両方を持ち合わせている - 通常は計算速度と精度の妥協点となる |
特徴量の標準化
特徴量の標準化（平均０、分散１）のようなスケーリングをした方が、勾配降下法の学習をより素早く収束化させることができる。
演習
ここから、実際のデータを使ってコードと学習の様子をグラフで書く。上記で学んだことを使用する（以下、概要）。
・特徴量を標準化
・学習率スケジューラーを使用（ReduceLROnPlateauを線形回帰問題に、ステップ減衰を二値分類に）
・各ステップごとに損失関数を記録する
・確率的勾配降下法（SGD）を使う
sklearnの線形回帰やロジスティック回帰は、トレーニング中の損失関数を監視する機能がないため、pytorchを使う必要がある。
Python verion == 3.10.4
numpy version == 2.2.5
matplotlib version == 3.10.1
sklearn version == 1.6.1
torch version == 2.7.0
演習１（線形回帰）
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from torch import nn, optim
import torch
np.random.seed(0) # 乱数のシードを設定
# データの生成（1次元の線形データ）
np.random.seed(0)
X = 2 * np.random.rand(100, 1) # 入力データ（特徴量）2*(0から1)の値を持つ100個のサンプル
y = 4 + 3 * X + np.random.randn(100, 1) # 目標データ（ターゲット）
# 特徴量の標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Pytorch用にTernsorに変換
X_tensor = torch.tensor(X_scaled, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32)
# モデルの定義（線形回帰）
model = nn.Linear(1, 1) # 線形回帰モデル
# 損失関数と最適化手法の定義
criterion = nn.MSELoss() # 平均二乗誤差
optimizer = optim.SGD(model.parameters(), lr=0.1) # 確率的勾配降下法
# 学習率スケジューラーの定義
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', patience=10, factor=0.5, min_lr=1e-6)
# 訓練パラメータ
n_epochs = 1000
losses = []
# モデルの訓練
for epoch in range(n_epochs):
# 順伝播
y_pred = model(X_tensor)
# 損失の計算
loss = criterion(y_pred, y_tensor)
losses.append(loss.item())
# 勾配の初期化
optimizer.zero_grad()
# 逆伝播
loss.backward()
# パラメータの更新
optimizer.step()
# 学習率スケジューラーのステップ
scheduler.step(loss)
# 学習率を取得
current_lr = optimizer.param_groups[0]['lr']
if epoch % 100 == 0: # 100回ごとに損失を出力
print(f"Epoch {epoch}: Loss = {loss.item():.4f}, Learning Rate = {current_lr:.6f}") # 学習過程での損失関数と学習率を監視
# 最終的な損失関数
print(f"Final Loss(MSE): {loss.item():.4f}")
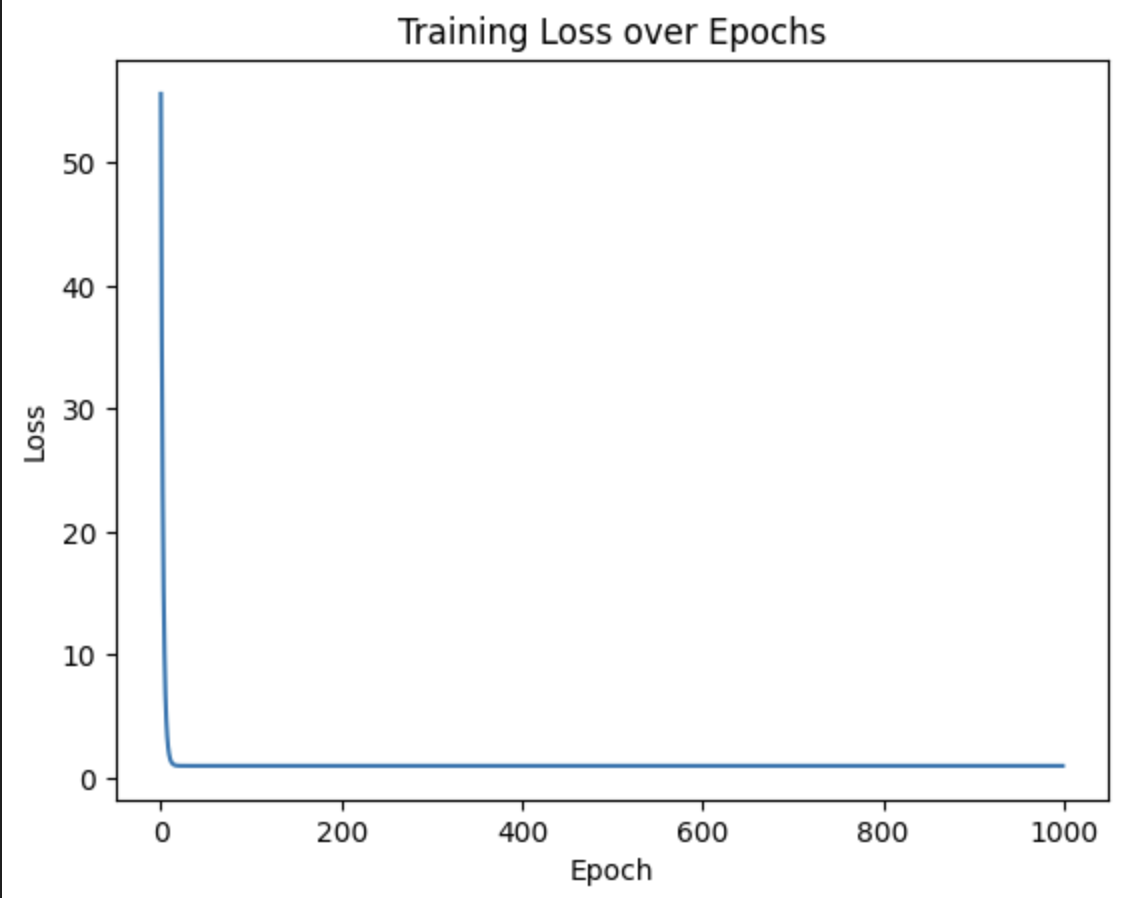
# 学習過程の損失関数のグラフ
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.show()
# 学習結果の可視化
plt.scatter(X_scaled, y, color='blue', label='Given Data')
plt.plot(X_scaled, model(X_tensor).detach().numpy(), color='red', label='Fitted line (Predicition from our model)')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Fitted Line on Given Data')
plt.legend()
plt.show()
# 結果
Epoch 0: Loss = 55.5918, Learning Rate = 0.100000
Epoch 100: Loss = 0.9924, Learning Rate = 0.001563
Epoch 200: Loss = 0.9924, Learning Rate = 0.000003
Epoch 300: Loss = 0.9924, Learning Rate = 0.000001
Epoch 400: Loss = 0.9924, Learning Rate = 0.000001
Epoch 500: Loss = 0.9924, Learning Rate = 0.000001
Epoch 600: Loss = 0.9924, Learning Rate = 0.000001
Epoch 700: Loss = 0.9924, Learning Rate = 0.000001
Epoch 800: Loss = 0.9924, Learning Rate = 0.000001
Epoch 900: Loss = 0.9924, Learning Rate = 0.000001
Final Loss (MSE): 0.9924
演習２（二値分類）
# 2クラス分類データの生成
# make_classification関数を使用して、1000サンプル、20特徴量のデータを生成
# n_informative=2: 説明力のある特徴量を2つだけ生成
# n_classes=2: 2クラス分類の問題
np.random.seed(0)
X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_classes=2, random_state=42)
# 特徴量の標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# PyTorch用にデータを変換
X_tensor = torch.tensor(X_scaled, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long) # バイナリ分類なので、ターゲットはlong型
# モデルの定義（シンプルなニューラルネット）
class LogisticRegressionModel(nn.Module):
def __init__(self, input_dim):
super(LogisticRegressionModel, self).__init__()
self.linear = nn.Linear(input_dim, 2) # 2クラス分類
def forward(self, x):
return self.linear(x)
# モデルのインスタンス化
model = LogisticRegressionModel(input_dim=20)
# 損失関数と最適化手法の定義
criterion = nn.CrossEntropyLoss() # クロスエントロピー損失（分類問題）
optimizer = optim.SGD(model.parameters(), lr=0.1)
# 学習率スケジューラーの定義
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=100, gamma=0.5)
# 訓練パラメータ
n_epochs = 1000
losses = []
# モデルの訓練
for epoch in range(n_epochs):
# 順伝播
y_pred = model(X_tensor)
# 損失の計算
loss = criterion(y_pred, y_tensor)
losses.append(loss.item())
# 勾配の初期化
optimizer.zero_grad()
# 逆伝播
loss.backward()
# パラメータの更新
optimizer.step()
# 学習率スケジューラーのステップ
scheduler.step()
# 学習率を取得
current_lr = optimizer.param_groups[0]['lr']
if epoch % 100 == 0: # 10回ごとに損失を出力
print(f"Epoch {epoch}: Loss = {loss.item():.4f}, Learning Rate = {current_lr:.6f}") # 学習過程での損失関数と学習率を監視
# 最終的な損失関数
print(f"Final Loss: {loss.item():.4f}")
# Accuracyの計算
with torch.no_grad(): # 評価モードで勾配計算を無効に
y_pred_class = model(X_tensor).argmax(dim=1) # 予測クラスを取得
accuracy = (y_pred_class == y_tensor).sum().item() / y_tensor.size(0) # 精度を計算
print(f"Accuracy: {accuracy:.4f}")
# 学習過程の損失関数のグラフ
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Over Time')
plt.show()
# 結果
Epoch 0: Loss = 0.8619, Learning Rate = 0.100000
Epoch 100: Loss = 0.3328, Learning Rate = 0.050000
Epoch 200: Loss = 0.3289, Learning Rate = 0.025000
Epoch 300: Loss = 0.3280, Learning Rate = 0.012500
Epoch 400: Loss = 0.3277, Learning Rate = 0.006250
Epoch 500: Loss = 0.3276, Learning Rate = 0.003125
Epoch 600: Loss = 0.3276, Learning Rate = 0.001563
Epoch 700: Loss = 0.3275, Learning Rate = 0.000781
Epoch 800: Loss = 0.3275, Learning Rate = 0.000391
Epoch 900: Loss = 0.3275, Learning Rate = 0.000195
Final Loss: 0.3275
Accuracy: 0.8770
本記事では、機械学習教師あり学習の重みの最適化として、勾配降下法を扱った。勾配降下法以外の最適化手法もあることを忘れてはいけない。