目的
市町村別人口を集計すると、二八の法則になる都道府県はどこか、を調べる。
二八の法則とは、「経済において、全体の数値の大部分は、全体を構成するうちの一部の要素が生み出しているとした。」wikipediaより引用。
市町村別人口に、二八の法則を当てはめると、都道府県全体の人口の8割は、2割の市町村に集まっている、となるので、実際どうなのか、最も当てはまりのよい都道府県はどこかを調べる。
二八の法則だけでなく、分析を通して、面白いことがわかれば、さらに分析を進める。
きっかけ
先日、「国勢調査で実践する初心者のためのPythonデータ分析ハンズオンセミナー」を受講しました。セミナーを受講して、国勢調査データで、何らかのデータ分析をしたいと思いました。
本内容は、その内容を参考とさせていただいております。セミナーの資料やnotebookは、GitHubに公開されていますが、興味がありましたら、ぜひ、書籍もご参照ください。
国勢調査データのダウンロードと前処理
まず、セミナーで使用していたデータ年齢(5歳階級、4区分)別、男女別人口を全都道府県分ダウンロードする。
これを前処理する必要があるが、セミナー資料として提供されている前処理関数をそのまま使用する。自分で追加したのは、以下の2点。
- 市区町村のみ抽出
HYOSYO が、自治体レベル(都道府県、市区町村、字、丁目)なので、今回は市町村レベルで二八の法則にあてはまるか調べたいので、市区町村のみを抽出する。 - 不要なデータを削除
データが冗長になるので、不要なデータ(自治体レベルHYOSYOなど)を削除する。
import pandas as pd
import numpy as np
import unicodedata
def prepro_kokusei(data_path: str) -> pd.DataFrame:
'''
国勢調査の統計データを前処理する関数
Params:
data_path: str
zip_fileのあるパス
Returns:
df: pd.DataFrame
前処理済みのデータ
'''
df = pd.read_csv(data_path, encoding='cp932', header=[0, 1])
front_col = [col for col in df.columns.get_level_values(0) if not col.startswith('T00')]
back_col = [col for col in df.columns.get_level_values(1) if not col.startswith("Unnamed:")]
new_col = front_col + back_col
df.columns = new_col
for col in df.loc[:, '総数、年齢「不詳」含む':].columns:
df[col] = pd.to_numeric(df[col], errors='coerce').fillna(0).astype(int)
# 変更用の辞書を作成
henko_dict = {
'年齢「不詳」含む': 'all',
'総数': 'total_',
'男': 'men_',
'女': 'women_',
'の': '',
'、': '',
'歳': '_age',
'未満': '_less',
'以上': '_over',
'~': '_'
}
# 変更したいカラム名のリストを変数に格納
cols = list(df.columns)
# 変更用の辞書を反映する
for k, v in henko_dict.items():
cols = [col.replace(k, v) for col in cols]
# 全角の数値を半角に変換
cols = [unicodedata.normalize('NFKC', col) for col in cols]
# カラム名を作成したものに置き換え
df.columns = cols
# 市区町村のみ抽出
df = df[df['HYOSYO']==1]
# 不要なデータを削除
df.drop(['HYOSYO','NAME','HTKSYORI','HTKSAKI', 'GASSAN'],axis=1,inplace=True)
return df
データ処理(福島県)
福島県のデータを読み込んでみる
df = prepro_kokusei('./data/tblT001082C07.zip') # 福島県
print(df.head())
print(df.columns)
KEY_CODE CITYNAME total_all total_0_4_age total_5_9_age \
0 7201 福島市 282693 9288 10403
277 7202 会津若松市 117376 3978 4651
538 7203 郡山市 327692 12096 13227
2276 7204 いわき市 332931 11351 12780
2806 7205 白河市 59491 2041 2366
...
[5 rows x 62 columns]
Index(['KEY_CODE', 'CITYNAME', 'total_all', 'total_0_4_age', 'total_5_9_age',
'total_10_14_age', 'total_15_19_age', 'total_20_24_age',
'total_25_29_age', 'total_30_34_age', 'total_35_39_age',
'total_40_44_age', 'total_45_49_age', 'total_50_54_age',
'total_55_59_age', 'total_60_64_age', 'total_65_69_age',
'total_70_74_age', 'total_15_age_less', 'total_15_64_age',
'total_65_age_over', 'total_75_age_over', 'men_total_all',
'men_0_4_age', 'men_5_9_age', 'men_10_14_age', 'men_15_19_age',
'men_20_24_age', 'men_25_29_age', 'men_30_34_age', 'men_35_39_age',
'men_40_44_age', 'men_45_49_age', 'men_50_54_age', 'men_55_59_age',
'men_60_64_age', 'men_65_69_age', 'men_70_74_age', 'men_15_age_less',
'men_15_64_age', 'men_65_age_over', 'men_75_age_over',
'women_total_all', 'women_0_4_age', 'women_5_9_age', 'women_10_14_age',
'women_15_19_age', 'women_20_24_age', 'women_25_29_age',
'women_30_34_age', 'women_35_39_age', 'women_40_44_age',
'women_45_49_age', 'women_50_54_age', 'women_55_59_age',
'women_60_64_age', 'women_65_69_age', 'women_70_74_age',
'women_15_age_less', 'women_15_64_age', 'women_65_age_over',
'women_75_age_over'],
dtype='object')
総数(total_all)や、5歳刻みの人口が市町村別に格納されていることがわかる。
これを、指定列(複数可能)について、人口を集計し、降順にソートする関数を用意する。
# 人口を集計し、降順にソート
# col_list は複数可能
def sort_by_population(df,col_list):
# 年代別人口を合計
df['sum'] = df[col_list].sum(axis=1)
# 人口の降順にソート
df.sort_values('sum',ascending=False,inplace=True)
return df
df = sort_by_population(df,['total_all'])
続いて、都道府県全体の人口の8割を占める市町村の数や割合を計算する関数を用意する。
人口8割を初めて超過する市町村までを含めたいので、人口昇順で(少ない順に)累積相対度数を求め、2割未満の市町村の数を求め、全体の数から引き算する。
また、後でグラフ化する際にも使えるので、市町村の数などの情報もクラス化してまとめておくようにする。
class PopulationInfo: # 都道府県の人口情報
def __init__(self,pref_name,pop_total,city_num,city_80_num,city_80_per) -> None:
self.pref_name = pref_name # 都道府県名称
self.pop_total = pop_total # 都道府県総人口
self.city_num = city_num # 市町村の数
self.city_80_num = city_80_num # 人口8割(超)を構成する市町村の数
self.city_80_per = city_80_per # 人口8割(超)を構成する市町村の割合
def print(self):
print(f'{self.pref_name} 総人口{self.pop_total} 市町村の数{self.city_num} 人口8割市町村の数{self.city_80_num} 割合{self.city_80_per:.2f}%')
# 都道府県全体の人口の8割を占める市町村の数や割合を計算
def get_population_info(df,pref_name):
pop_total = df['sum'].sum() # 都道府県総人口
city_num = df.shape[0] # 市町村の数
pop_sum = df['sum'].sort_values() # 逆順(昇順)の人口
ref = pop_sum / pop_total # 昇順人口の相対度数
cum = ref.cumsum() # 昇順人口の累積度数
city_20_num = (cum<0.2).sum() # 人口2割(未満)を構成する市町村の数
city_80_num = city_num - city_20_num # 人口8割(超)を構成する市町村の数
city_80_per = (city_80_num/city_num)*100 # 人口8割(超)を構成する市町村の割合
return PopulationInfo(pref_name,pop_total,city_num,city_80_num,city_80_per)
pop_info = get_population_info(df,'福島県')
pop_info.print()
福島県 総人口1833152 市町村の数59 人口8割市町村の数12 割合20.34%
福島県の場合、20.34% となり、かなり二八の法則に近い。
前処理(区の扱い)
他の都道府県でも実行するが、その前に、東京特別区や政令指定都市(区)について、考えておく必要がある。
(受講したセミナーでも、前処理が大切で大変なステップ、との説明があった通りである。)
国勢調査データでは、市単位ではなく、区単位で人口データをまとめているでの、そのままでは、各区で1市町村にカウントされる。
もともと同じ一つの市(東京市も含めて)であったのが、大都市化したため区ができたので、人口集中しているか、という観点では、一つの市とすべきであろうということから、今回は、区はまとめて一つの市とする。
区をマージすべきかについては、参考(区をマージしなかった場合)でも後述する。
政令指定都市(東京特別区)の区をマージする関数を用意する。以下、2点がポイント
- 政令指定都市(市区町村名に市がある)と東京特別区(市区町村名に市がない)の区別が必要。
- 一つの都道府県に、複数の政令指定都市がある場合の対応が必要。
前者はifで場合分けをし、後者は再帰呼び出しで対応した。
# 政令指定都市の区をマージ
def merge_designated_city(df):
# 区で終わるCITYNAMEを取得
df_designated_city = df[df['CITYNAME'].str.endswith('区')]
if df_designated_city.shape[0]==0:
return df # 政令指定都市がない
# マージした区の最初のインデックス
index = df_designated_city.index[0]
# その区は、市を含むか?(東京特別区の処理)
designated_cityname = df_designated_city.loc[index,'CITYNAME']
if '市' in designated_cityname:
pos = designated_cityname.find('市')
designated_cityname = designated_cityname[0:pos+1] # 政令指定都市名称
# 政令指定都市を取得(他の政令指定都市の区を除外して再取得)
df_designated_city = df[df['CITYNAME'].str.startswith(designated_cityname)]
# 政令指定都市以外を取得
df_wo_designated_city = df[~df['CITYNAME'].str.startswith(designated_cityname)]
else:
designated_cityname = '東京特別区'
# 政令指定都市以外を取得
df_wo_designated_city = df[~df['CITYNAME'].str.endswith('区')]
df_designated_city = df_designated_city.sum(axis=0) # 各区の人口を合算
df_designated_city['CITYNAME'] = designated_cityname # 政令指定都市名称
df_designated_city = pd.DataFrame(df_designated_city) # Series -> Dataframe 変換
df_designated_city = df_designated_city.T # 転置
df_designated_city['index'] = index # 最初の区のインデックス
df_designated_city.set_index('index',inplace=True) # インデックス化
# 政令指定都市と、政令指定都市以外をマージ
df = pd.concat( [df_wo_designated_city,df_designated_city],axis=0)
# 複数の政令指定都市がある場合(再帰呼び出し)
if '市' in designated_cityname:
return merge_designated_city(df)
else:
return df # 東京特別区
df = prepro_kokusei('./data/tblT001082C27.zip') # 大阪
print(df.head())
df = merge_designated_city(df)
print(df.tail())
KEY_CODE CITYNAME total_all total_0_4_age total_5_9_age \
0 27102 大阪市都島区 107904 3785 4069
62 27103 大阪市福島区 79328 3737 3174
111 27104 大阪市此花区 65251 2300 2595
190 27106 大阪市西区 105862 4769 4148
268 27107 大阪市港区 80948 2599 2665
...
KEY_CODE CITYNAME total_all total_0_4_age total_5_9_age total_10_14_age \
10556 27381 太子町 13009 416 529 608
10568 27382 河南町 15697 439 570 676
10604 27383 千早赤阪村 4909 98 137 182
0 650778 大阪市 2752412 96980 96876 96793
2422 190008 堺市 826161 30149 34179 37763
大阪の場合、大阪市と堺市が区単位であったのを、市単位でまとめることができた。
上側が処理前(大阪市都島区など)で、下側が処理後(大阪市と堺市が最後に追加されている。)
分析結果
各都道府県で処理し、二八の法則に当てはまりの良い都道府県を調べることにする。
ダウンロードした国勢調査データは、都道府県番号で識別できるので、総務省の都道府県コード表をダウンロードし、pref_list.csv を作成した。
pref_list = pd.read_csv('./data/pref_list.csv',index_col=0)
print(pref_list.head())
都道府県名
番号
1 北海道
2 青森県
3 岩手県
4 宮城県
5 秋田県
これを使って、都道府県をループし、処理する。
後で分析しやすいように、データフレーム化しておく。
# 都道府県の人口情報リスト
pop_info_list = {}
# データフレーム化のためのリスト
pref_name_list = []
pop_total_list = []
city_num_list = []
city_80_num_list = []
city_80_per_list = []
df_list = {}
# 都道府県のループ
for pref_no, row in pref_list.iterrows():
# 都道府県名称
pref_name = row['都道府県名']
# ファイル名称
filename = './data/tblT001082C' + str(pref_no).zfill(2) + '.zip'
# 読み込みと前処理
df = prepro_kokusei(filename)
# 政令指定都市の区をマージ
df = merge_designated_city(df)
# 人口を集計し、降順にソート
df = sort_by_population(df,['total_all'])
# 都道府県全体の人口の8割を占める市町村の数や割合を計算
pop_info = get_population_info(df,pref_name)
# 都道府県の人口情報リストに追加
pop_info_list.update({pref_name:pop_info})
# データフレーム化のためのリストに追加
pref_name_list.append(pop_info.pref_name)
pop_total_list.append(pop_info.pop_total)
city_num_list.append(pop_info.city_num)
city_80_num_list.append(pop_info.city_80_num)
city_80_per_list.append(pop_info.city_80_per)
# データフレームの格納
df_list.update({pref_name:df})
# リストをデータフレーム化
df_pop_info = pd.DataFrame()
df_pop_info['都道府県名'] = pref_name_list
df_pop_info.set_index('都道府県名',inplace=True)
df_pop_info['都道府県総人口'] = pop_total_list
df_pop_info['市町村の数'] = city_num_list
df_pop_info['人口8割(超)を構成する市町村の数'] = city_80_num_list
df_pop_info['人口8割(超)を構成する市町村の割合'] = city_80_per_list
# 2割との差(絶対値)を計算
df_pop_info['人口8割(超)を構成する市町村の割合の2割との差'] = abs(df_pop_info['人口8割(超)を構成する市町村の割合']-20)
# 2割との差(絶対値)の昇順にソート
df_pop_info.sort_values('人口8割(超)を構成する市町村の割合の2割との差',inplace=True)
# トップ5を表示
print(df_pop_info.head())
都道府県総人口 市町村の数 人口8割(超)を構成する市町村の数 人口8割(超)を構成する市町村の割合 人口8割(超)を構成する市町村の割合の2割との差
都道府県名
福島県 1833152.0 59 12 20.338983 0.338983
神奈川県 9237337.0 33 8 24.242424 4.242424
長野県 2048011.0 77 19 24.675325 4.675325
岡山県 1888432.0 27 7 25.925926 5.925926
北海道 5224614.0 179 25 13.966480 6.033520
福島県が、20%にもっとも近く、誤差がわずか0.34%。
二位は神奈川県で、誤差4.24%。
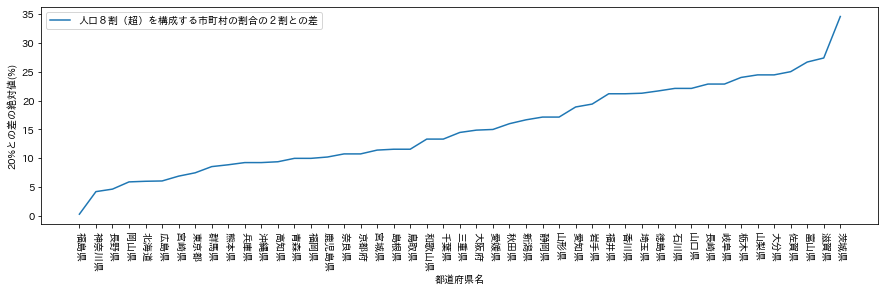
全都道府県の割合の20%からの差の絶対値を可視化してみる。
from matplotlib import pyplot as plt
import japanize_matplotlib
fig, ax1 = plt.subplots(figsize=(15, 4))
df_pop_info.plot(y='人口8割(超)を構成する市町村の割合の2割との差',ax=ax1)
ax1.set_ylabel('20%との差の絶対値(%)')
ax1.set_xticks(range(0,df_pop_info.shape[0]))
ax1.set_xticklabels(df_pop_info.index,rotation=270)
plt.show()
20%にもっとも近いのは福島県、20%からもっとも離れているのは茨城県とわかる。
隣り合う福島県と茨城県が、人口集中度合いが真逆になっているのがおもしろい。
これがどのような状態になっているかを、人口の累積相対度数のグラフで見てみる。
横軸に人口降順の市町村、縦軸に人口(棒グラフ)と累積相対度数を表示する。
# 人口の累積相対度数を可視化
def plot_population(df,pop_info):
# グラフ表示
fig, ax1 = plt.subplots(figsize=(20, 4))
# タイトル
ax1.set_title(pop_info.pref_name )
# 人口
df.plot.bar(x='CITYNAME', y='sum', ax=ax1, width=1, ec='k', lw=2)
ax1.get_legend().remove()
# 相対累積度数
ref = df['sum'] / pop_info.pop_total # 相対度数
cum = ref.cumsum() # 累積度数
ax2 = ax1.twinx()
ax2.plot(np.arange(pop_info.city_num), cum, '--o', color='k')
ax2.set_ylabel('累積相対度数')
# 人口80%ラインを表示(赤の一点鎖線)
x = [0, pop_info.city_num]
y = [0.8, 0.8]
ax2.plot(x,y, color='red', linestyle='dashdot')
# 人口80%を構成する市町村ライン(赤実線)
x = [pop_info.city_80_num-1, pop_info.city_80_num-1]
y = [0, 1]
ax2.plot(x,y, color='red', linestyle='solid', linewidth=5 )
# 市町村20%ラインを表示(赤の一点鎖線)
x = [pop_info.city_num*0.2, pop_info.city_num*0.2]
y = [0, 1]
ax2.plot(x,y, color='red', linestyle='dashdot')
plt.show()
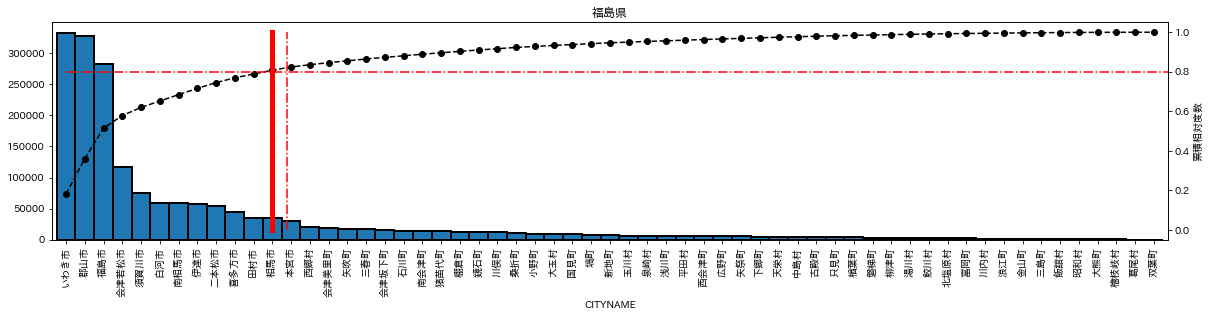
plot_population(df_list['福島県'],pop_info_list['福島県'])
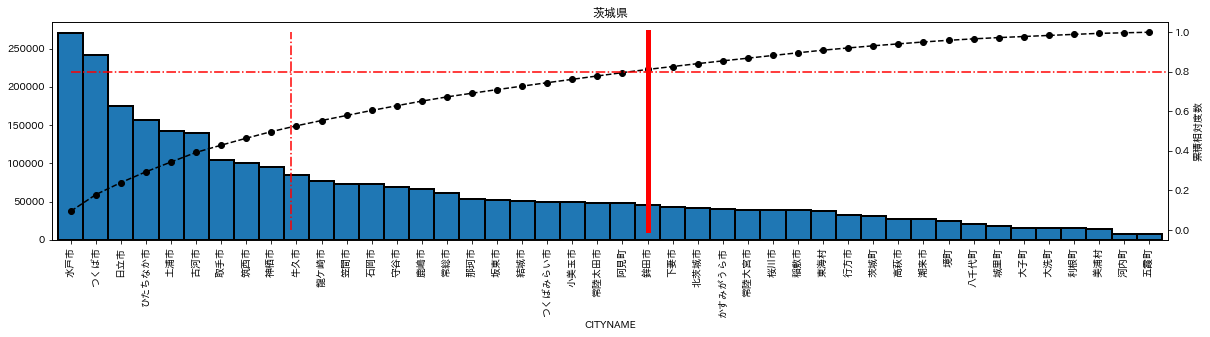
plot_population(df_list['茨城県'],pop_info_list['茨城県'])
福島県は、人口80%を構成する市町村ライン(赤実線)と、市町村20%ライン(赤の一点鎖線)が近いのに対し、茨城県は離れている。
全都道府県の処理(タイプ分類)
全都道府県で可視化した。紙面の都合上、特徴ある都道府県についてのみ、以下、タイプ別に表示する。
二八の法則より集中
まず、人口80%を構成する市町村の数が、20%以下となるのは、北海道と東京都の2都道。
札幌市、東京特別区への一極集中のみならず、全体的にも粗密が激しい。
8割の人口は、わずか12~13%の市に集まっている。
北海道は、市町村の数が多すぎる(断トツの179)ので致し方ないか。面積が広いので、市町村合併にも無理があるのだろう。
東京都は、区部への一極集中は、都レベルでなく、国レベルでの現象なので、止められないどころか、ますます集中していくのだろう。
plot_population(df_list['北海道'],pop_info_list['北海道'])
plot_population(df_list['東京都'],pop_info_list['東京都'])
pop_info_list['北海道'].print()
pop_info_list['東京都'].print()
北海道 総人口5224614.0 市町村の数179 人口8割市町村の数25 割合13.97%
東京都 総人口14047594.0 市町村の数40 人口8割市町村の数5 割合12.50%
1都市集中(1位都市の人口が、2位都市の人口のおおよそ2倍以上と定義)
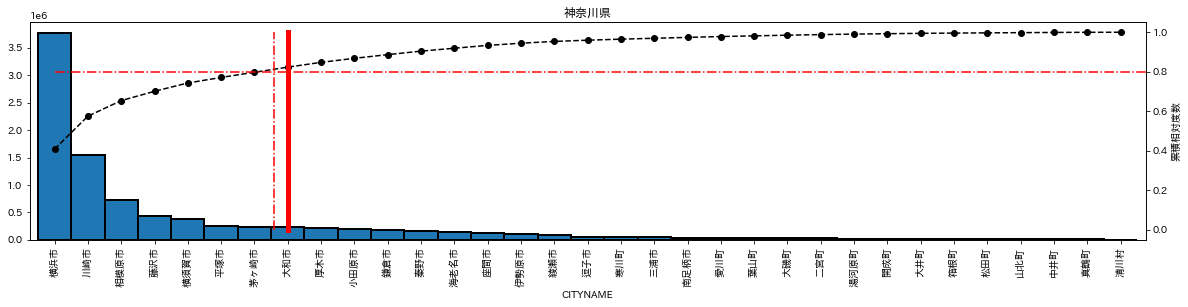
宮城県のような政令指定都市が1つある県のみでなく、神奈川県のように複数の政令指定都市がある県でも、中心都市への集中が激しい。
政令指定都市がなくとも、高知県や熊本県など、県庁所在地への人口集中度が高い。
plot_population(df_list['宮城県'],pop_info_list['宮城県'])
plot_population(df_list['神奈川県'],pop_info_list['神奈川県'])
plot_population(df_list['高知県'],pop_info_list['高知県'])
plot_population(df_list['熊本県'],pop_info_list['熊本県'])
複数都市集中(1位以外の上位都市の人口が、一つ下位の都市の人口のおおよそ2倍以上と定義)
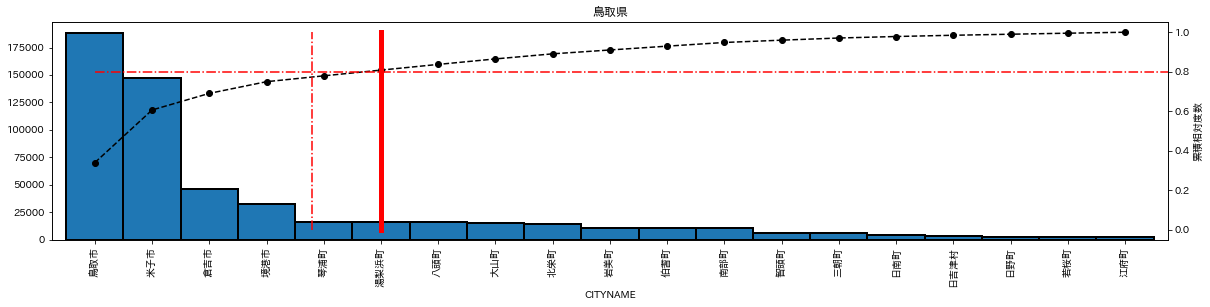
福島県もそうだが、青森県(青森市、八戸市、弘前市)や鳥取県(鳥取市、米子市)などは、複数都市への集中が見られる。
江戸時代は違う国(藩)だったのが、廃藩置県で、同じ県にまとまったためと考えられ、同じ県内で良きライバルとして競い合っているのだろう。
例えるなら、魏呉蜀の三国時代であり、個人的には、このような県は味(個性)があっておもしろいと思う。
plot_population(df_list['青森県'],pop_info_list['青森県'])
plot_population(df_list['鳥取県'],pop_info_list['鳥取県'])
まんべんなく分散(一つ下位の都市に、おおよそ2倍以上の差をつける都市がない、と定義)
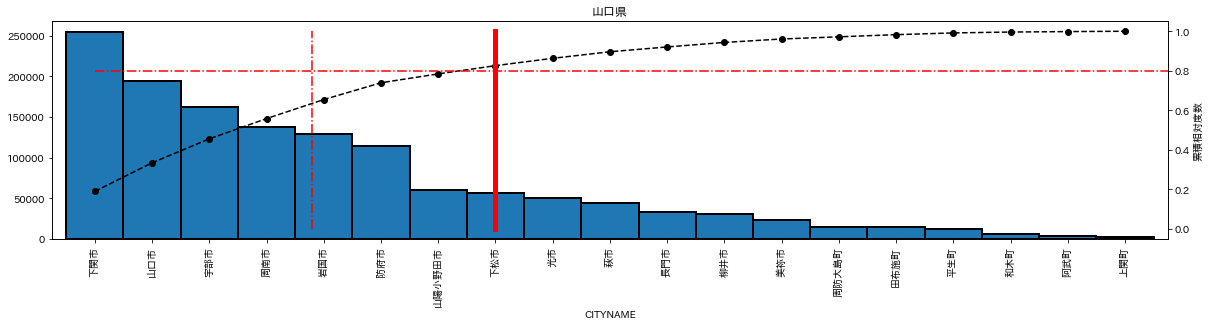
茨城県もそうだが、三重県や山口県などは、人口集中する都市はなく、まんべんなく人口が多い。
これは、群雄割拠の戦国時代とでもいうべきか。県庁所在地の人口を凌駕する都市が現れ、まさに下剋上である。水戸市の人口もつくば市に抜かれるのは時間の問題か?
plot_population(df_list['三重県'],pop_info_list['三重県'])
plot_population(df_list['山口県'],pop_info_list['山口県'])
参考(区をマージしなかった場合)
政令指定都市の区をマージしなかった場合を表示してみる。
df = prepro_kokusei('./data/tblT001082C27.zip') # 大阪府
df = sort_by_population(df,['total_all'])
pop_info = get_population_info(df,'大阪府(区マージせず)')
plot_population(df,pop_info)
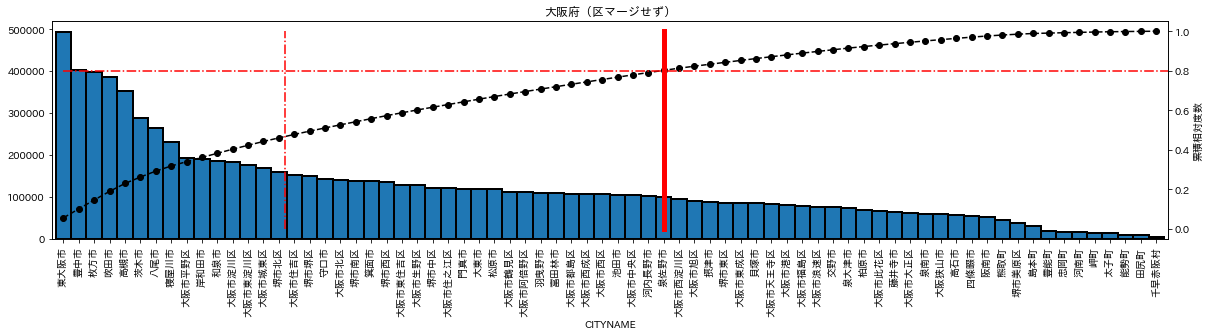
東大阪市が人口1位となり、実態とあってないように見える。
やはり区をマージした下図のほうが実態とあっていると思う。
plot_population(df_list['大阪府'],pop_info_list['大阪府'])
まとめ
二八の法則は、福島県がもっとも当てはまりがよい。当てはまりが悪いのは、お隣の茨城県。
二八の法則で分析した結果、ふ~ん、で終わっちゃう感じでしたが、市町村別の人口分布のほうが面白いことがわかりました。
二八の法則より集中しているタイプ(東京都、北海道)、1都市集中タイプ(宮城県、神奈川県、高知県、熊本県など)、複数都市集中タイプ(福島県、青森県、鳥取県など)、分散タイプ(茨城県、三重県、山口県など)に分類できました。
みなさんは、市町村別の人口分布については、どのタイプがお好きでしょうか?私は前述の通り、複数都市集中タイプの三国時代ですかね。
あと、分散タイプの群雄割拠しているなかでの下剋上(水戸市vsつくば市など)についても面白いですね。今後、注視していきたいです。
紙面の都合上、全都道府県のタイプ/グラフは表示しませんでしたが、興味がありましたら、お住まいの都道府県についても可視化してみてください。