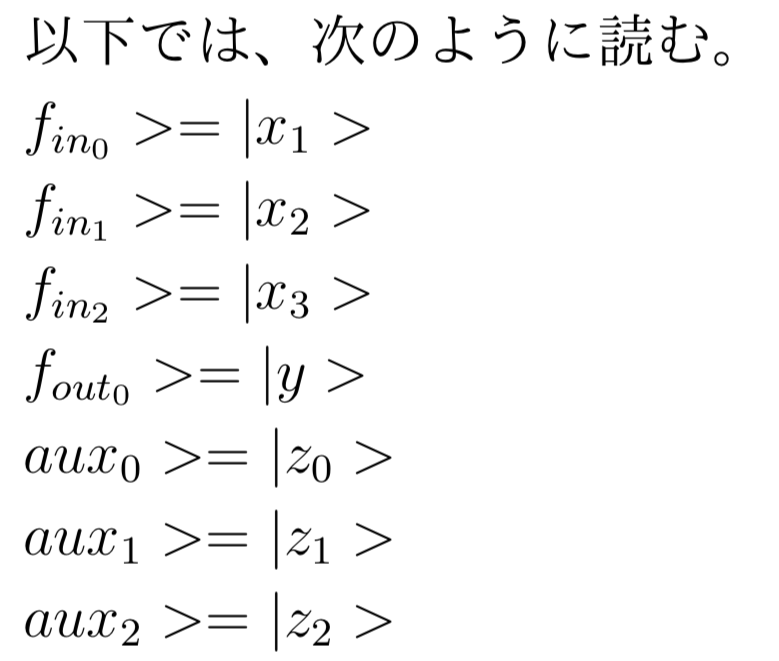量子コンピュータで動くアルゴリズムを設計しましょう
量子コンピュータ
を知って、少し or かなり関心のある方はいるでしょう。
そろそろ、具体的なアルゴリズムを作成したくありませんか?
ここでは、
Open Source Quantum Information Software Kit ( https://qiskit.org/ )
を使用して、量子コンピュータで動く、アルゴリズム(グローバーのアルゴリズムを使用)の設計の一例を紹介します。
An Introduction to Quantum Computing, Without the Physics(https://arxiv.org/abs/1708.03684)
では、具体的なアルゴリズムの量子ゲートでの書き方が解説されていますので、
これを参考に。
この記事は、全体的にやや量子情報(*)の学習をした経験のある方向けです。
なんとなく、中身をざっと見て、判断していただけると幸いです。
*量子ビット, 量子ゲート, グローバーのアルゴリズムの仕組みを知っている程度。
物理の知識は一切必要なし(Without the Physics)。
ただし、SAT問題などは知っておいたほうが良い。
ちなみに、この資料は大学院のセミナーで使用したもの。
量子コンピュータとは
量子コンピュータは、量子力学という物理学を生かした、コンピュータです。
最近(2018~2019年)は、非常に注目されている気がします。
量子コンピュータの計算方式にはいくつか種類がありますが、
ここでは、量子ゲート方式と呼ばれる手法でアルゴリズムを設計します。
量子アルゴリズムとは
先にのべた
Open Source Quantum Information Software Kit ( https://qiskit.org/ )
では、
量子アルゴリズムの解説がなされています。
量子アルゴリズムを開発すると、何が嬉しいのでしょう?
量子アルゴリズムは、従来のコンピュータで動かすアルゴリズムより、計算がはやいケースがあるのです!
この「はやい」は、計算回数が、従来のものより少ないという意味です。
すでに多くの量子アルゴリズムが開発されており(例えば以下のサイト)、
https://math.nist.gov/quantum/zoo/
量子コンピュータがより一層実用化された暁に、動くことを楽しみにしていることでしょう。
扱う問題
以下の論文(まとめ記事に近い) An Introduction to Quantum Computing, Without the Physics では、
https://arxiv.org/abs/1708.03684
物理、特に物理学の知識がなくとも、量子コンピューティングとその仕組みがわかるように解説されています。
特に、グローバーのアルゴリズム(後述)をExactly-1 in 3-SAT(これも後述)に適用する
qiskitのコードと共に紹介されています。
ここで紹介されている量子ゲートの動き、働きを解説します(日本語で!)。
グローバーのアルゴリズムって?
仕組みを知っている人を前提にしていますが、軽く触れます。
量子アルゴリズムの一つで探索アルゴリズムです。
ソートされていない1次元のデータベース(データ数($=N$) )から、ターゲットを探し出すことができます。
普段のアルゴリズムを考えてみましょう。
1つ1つのデータを適宜確かめなくてはならないので、計算回数のオーダーは、$O(N)$です。
しかし、グローバーのアルゴリズムはどうでしょう。
ターゲットが一つなら、データ数($=N$)に対し、$\frac{\pi}{4}\sqrt{N}$ほどの計算回数でターゲットが見つかります。
これは、明確にはやいですね!
ただし、この計算回数とは何かという問題がありますが、
一旦、「見つけたターゲットが探しているターゲットであるかどうかをチェックする回数」と考えてください。
Exactly-1 in 3-SAT って?
NP完全問題であるSATの変形問題です。
https://ja.wikipedia.org/wiki/%E5%85%85%E8%B6%B3%E5%8F%AF%E8%83%BD%E6%80%A7%E5%95%8F%E9%A1%8C
から引用します。<-- -->の範囲
<--
充足可能性問題(じゅうそくかのうせいもんだい、satisfiability problem, SAT)は、一つの命題論理式が与えられたとき、それに含まれる変数の値を偽 (False) あるいは真 (True) にうまく定めることによって全体の値を'真'にできるか、という問題をいう。SATisfiabilityの頭3文字を取ってしばしば「SAT」と呼ばれる。
任意の論理式からなる充足可能性問題はNP完全であるが、ある特殊な形状をもつ論理式のクラスに限定しても、なおNP完全であることが証明されている。
CNF-論理式 - 節の論理積からなるもの。
3-SAT - CNF-論理式のうち、節内のリテラル数が、高々3つのもの。
-->
言葉を整理しましょう。
- リテラル : ブール変数 or ブール変数の否定
- 節 : いくつかのリテラルを or演算子($\vee$の形をしているあれです)でつないだもの
- 論理積標準形(CNF論理式) : ブール論理式$f$が、$f =$ (節)$\wedge$(節)$\wedge$(節)・・・$\wedge$(節)の形をしているもの
ここから、
or演算子を $\vee$
and演算子を $\wedge$
排他的論理和を $\oplus$
not演算子を $\overline{x}$ (ブール変数$x$の否定)
と表します。
そして、Exactly-1 in 3-SATとは、
全ての節内において、3つのリテラルの真偽値はひとつのみ1で、他は0になっていることを要請します。
例えば、
$(x_{1} \vee x_{2} \vee \overline{x_{3}}) \wedge (\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{3}}) \wedge (\overline{x_{1}} \vee x_{2} \vee x_{3})$
というcnf論理式が与えられたら、
$x_{1} = 1, x_{2} = 0, x_{3} = 1$
が答えです。
アルゴリズムをかいてみる
ここまでで下準備ができたので、
コードをかいていきます。
ここに記載したコードは、私が作成したものではなく、
上記の論文に記載されていたものをペタッと貼り付けて、コメントに
日本語で解説を加えただけです。
このコードだけではなんのことやらとならないために、
この次の章で、解説があります。
ブール代数の初歩や基本的な量子ゲートの扱い、1-in-3SAT問題、グローバーのアルゴリズム
それ自体は理解しているものとする。あと、手元に量子ゲートの絵が無いときついと思うので下に解説と共に記載。
ここで、x,yは論理変数, X,Yはリテラル, +は排他的論理和, vはor, ^はand, notは否定演算子とする。
# まず、sysをimport。
import sys
# ここから
try:
sys.path.append("../../") # go to parent dir
import Qconfig
qx_config = {
"APItoken": Qconfig.APItoken,
"url": Qconfig.config['url']}
except:
qx_config = {
"APItoken":"your API Token", #ここに自分のAPITokenをかく!
"url":"https://quantumexperience.ng.bluemix.net/api"}
# ここまでは、エラーが起きないように処理しつつ、自分のAPITokenを使えるように準備してる。
# qiskitから色々importする。
from qiskit import QuantumProgram, QuantumCircuit
from qiskit.tools import visualization
# ここからしばらく、必要な量子ゲートの作成をするための関数を定義していく。
# 初期状態である、重ね合わせ状態を作成するための行列
def input_state(circuit, f_in, f_out, n):
"""(n+1)-qubit input state for Grover search."""
for j in range(n):
circuit.h(f_in[j])
circuit.x(f_out) #これは縁の下の力持ち的役割を果たしているね。
circuit.h(f_out)
# -- end function
# X_1 v X_2 v X_3 = (X_1 + X_2 + X_3) + (X_1 ^ X_2 ^ X_3)は下の章で解説してある。
# 以下で書いてある数式は全量子ビットの初期状態が|0>となっていることを仮定して、かいた。
# 今回の問題のオラクルを表す行列
def black_box_u_f(circuit, f_in, f_out, aux, n, exactly_1_3_sat_formula):
# 以下exactly_1_3_sat_formula = [[1, 2, -3], [-1, -2, -3], [-1, 2, 3]]としてコメントをかく。
# この式が表す意味は、論文を参照すること。
num_clauses = len(exactly_1_3_sat_formula)
for (k, clause) in enumerate(exactly_1_3_sat_formula):
#kは0,1,2をループする。clauseは、k=1のとき、[1, 2, -3]を表す。
for literal in clause: #k=1のとき、[1, 2, -3]のなかをループする。
if literal > 0: #リテラルが論理変数での否定の形をしていないとき(x)
circuit.cx(f_in[literal-1], aux[k])
else: #リテラルが論理変数の否定の形をしているとき(not x)
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
#ここまでで、aux[k] = x_1 + x_2 + not(x_3) などの形を表すゲートを書いてる。
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
#aux[num_clauses] = x_1 ^ x_2などの形を表すゲートを書いてる。
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
#aux[k] = X_1 v X_2 v X_3 = (X_1 + X_2 + X_3) + (X_1 ^ X_2 ^ X_3)の形を完成!
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
#aux[num_clauses]を初期化。
for literal in clause:
#リテラルが論理変数の否定の形をしているとき(not x)
#そこの量子ビットだけ初期化している。
if literal < 0:
circuit.x(f_in[-literal-1])
if (num_clauses == 1):
circuit.cx(aux[0], f_out[0])
elif (num_clauses == 2):
circuit.ccx(aux[0], aux[1], f_out[0])
elif (num_clauses == 3): #
circuit.ccx(aux[0], aux[1], aux[num_clauses])
circuit.ccx(aux[2], aux[num_clauses], f_out[0]) #f_out[0] = f(x_1,x_2,x_3)を完成!
circuit.ccx(aux[0], aux[1], aux[num_clauses])
else:
raise ValueError('We only allow at most 3 clauses')
#f_out[0] = f(x_1,x_2,x_3)以外の量子ビットを初期化するため、もう一度
#f_out[0]以外の量子ビットに行った演算をもう一度行う(because X + X = 0)
for (k, clause) in enumerate(exactly_1_3_sat_formula):
for literal in clause:
if literal > 0:
circuit.cx(f_in[literal-1], aux[k])
else:
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
for literal in clause:
if literal < 0:
circuit.x(f_in[-literal-1])
# -- end function
# n_controlled_Zゲート書いてる。見たまんま。
def n_controlled_Z(circuit, controls, target):
"""Implement a Z gate with multiple controls"""
if (len(controls) > 2):
raise ValueError('The controlled Z with more than 2 ' +
'controls is not implemented')
elif (len(controls) == 1):
circuit.h(target)
circuit.cx(controls[0], target)
circuit.h(target)
elif (len(controls) == 2):
circuit.h(target)
circuit.ccx(controls[0], controls[1], target)
circuit.h(target)
# -- end function
# グローバー行列(これは、おきまりの構築方法を書いてあるだけ。論文参照。)
def inversion_about_average(circuit, f_in, n):
"""Apply inversion about the average step of Grover's algorithm."""
for j in range(n):
circuit.h(f_in[j])
for j in range(n):
circuit.x(f_in[j])
n_controlled_Z(circuit, [f_in[j] for j in range(n-1)], f_in[n-1])
for j in range(n):
circuit.x(f_in[j])
for j in range(n):
circuit.h(f_in[j])
# -- end function
# ここまでで、初期状態を生成するゲート,オラクルを表すゲート,グローバー行列を表すゲートを作成できた。
# ここからアルゴリズムを動かす
if (__name__ == '__main__'):
# Make a quantum program for the n-bit Grover search.
n = 3
# Exactly-1 3-SAT formula to be satisfied, in conjunctive
# normal form. We represent literals with integers, positive or
# negative, to indicate a Boolean variable or its negation.
exactly_1_3_sat_formula = [[1, 2, -3], [-1, -2, -3], [-1, 2, 3]]
# Define three quantum registers: 'f_in' is the search space (input
# to the function f), 'f_out' is bit used for the output of function
# f, aux are the auxiliary bits used by f to perform its
# computation.
#ーーーーーここから
QPS_SPECS = { #今から必要な設定を宣言します。
'circuits': [{
'name': 'grover', #名前はgroverです。
'quantum_registers': [ #量子ビットは以下の通りです。
{'name': 'f_in', 'size': n}, #f_inという名前のサイズnの配列を用意します。
{'name': 'f_out', 'size': 1}, #f_outという名前のサイズ1の配列を用意します。
{'name': 'aux', 'size': len(exactly_1_3_sat_formula) + 1},
#auxという名前のサイズ len(exactly_1_3_sat_formula) + 1の配列を用意します。
],
'classical_registers': [ #観測に必要なレジスタは以下の通りです。
{'name': 'ans', 'size': n},#ansという名前のサイズnの配列を用意します。
]}]#
}
#ーーーーーここまでは、書き方を覚えるべし。
#この辺も鉄板の書き方。
qp = QuantumProgram(specs=QPS_SPECS)
qc = qp.get_circuit('grover')
f_in = qp.get_quantum_register('f_in')
f_out = qp.get_quantum_register('f_out')
aux = qp.get_quantum_register('aux')
ans = qp.get_classical_register('ans')
#重ね合わせ状態を作成。
input_state(qc, f_in, f_out, n)
#今回オラクルへの質問回数は2(か3)です(これは事前に計算可能)。
black_box_u_f(qc, f_in, f_out, aux, n, exactly_1_3_sat_formula)
inversion_about_average(qc, f_in, n)
black_box_u_f(qc, f_in, f_out, aux, n, exactly_1_3_sat_formula)
inversion_about_average(qc, f_in, n)
#観測
for j in range(n):
qc.measure(f_in[j], ans[j])
#今回は、local_qasm_simulatorで動かす。つまりはシミュレーションです。
result = qp.execute(['grover'], backend='local_qasm_simulator',
coupling_map=None, shots=2048)
#何回とある値が観測されたか、それぞれをカウント。
counts = result.get_counts('grover')
#ヒストグラムを表示。
visualization.plot_histogram(counts)
# To get this to work you need to make sure poppler is installed !!!
# というわけなので、気をつけて!!!
from qiskit.tools.visualization import circuit_drawer
circuit_drawer(qc)
#これで量子ゲートの絵が描ける。
Exactly-1 in 3-SAT の式変形
ここで、問題を量子ゲートでかけるように式変形をします。
量子ゲートの場合、Xゲートでnot素子を、
CCNOTゲートでand素子や排他的論理和を表現できます。
$(x_{1} \vee x_{2} \vee \overline{x_{3}}) \wedge (\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{3}}) \wedge (\overline{x_{1}} \vee x_{2} \vee x_{3}) = 1$
$\Leftrightarrow $
$x_{1} \vee x_{2} \vee \overline{x_{3}} = 1$
と
$\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{3}} = 1$
と
$\overline{x_{1}} \vee x_{2} \vee x_{3} = 1$
の全てが成立していること
に注意する。
以下の命題が成立します。
命題
$a \wedge b \wedge c = 1$かつ$a,b,c$の中で真$(=1)$は一つのみ
$\Leftrightarrow $ $(a \oplus b \oplus c)\oplus(a \vee b \vee
c)=1$
(証明は後述)
この命題を使用します。
量子ゲート(量子回路)を作成する
量子回路を実際に作成していきます。
多くのネット記事、雑誌、本が出ているので、そちらも参照しつつ。
CCNOTゲートについて以下のように作用することを注意します。
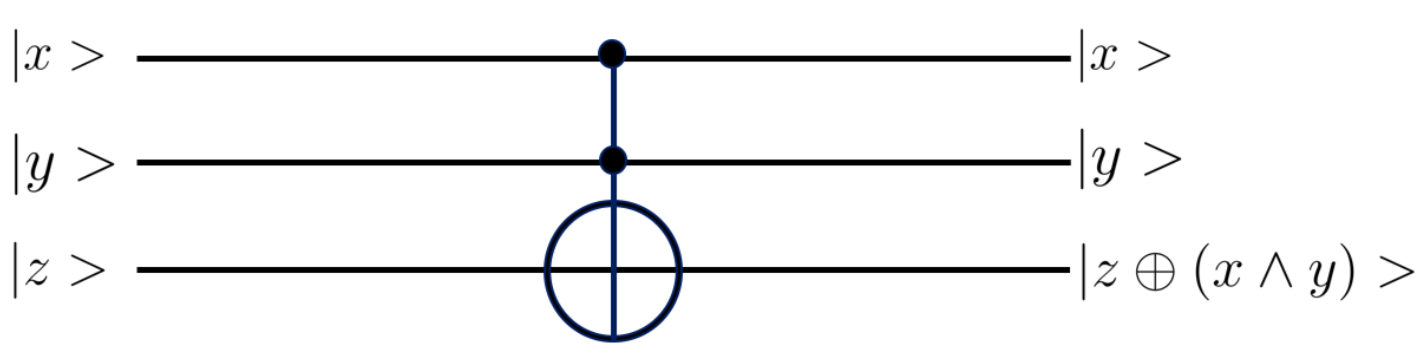
Exactly-1 in 3-SAT問題を考える論理式は、
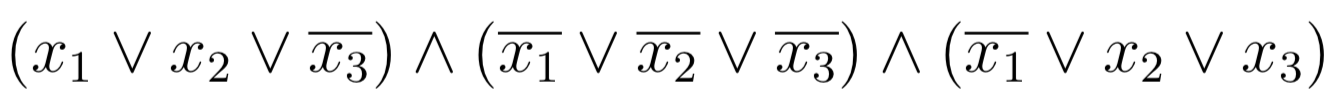
です。
これを解くアルゴリズムは以下の通り。

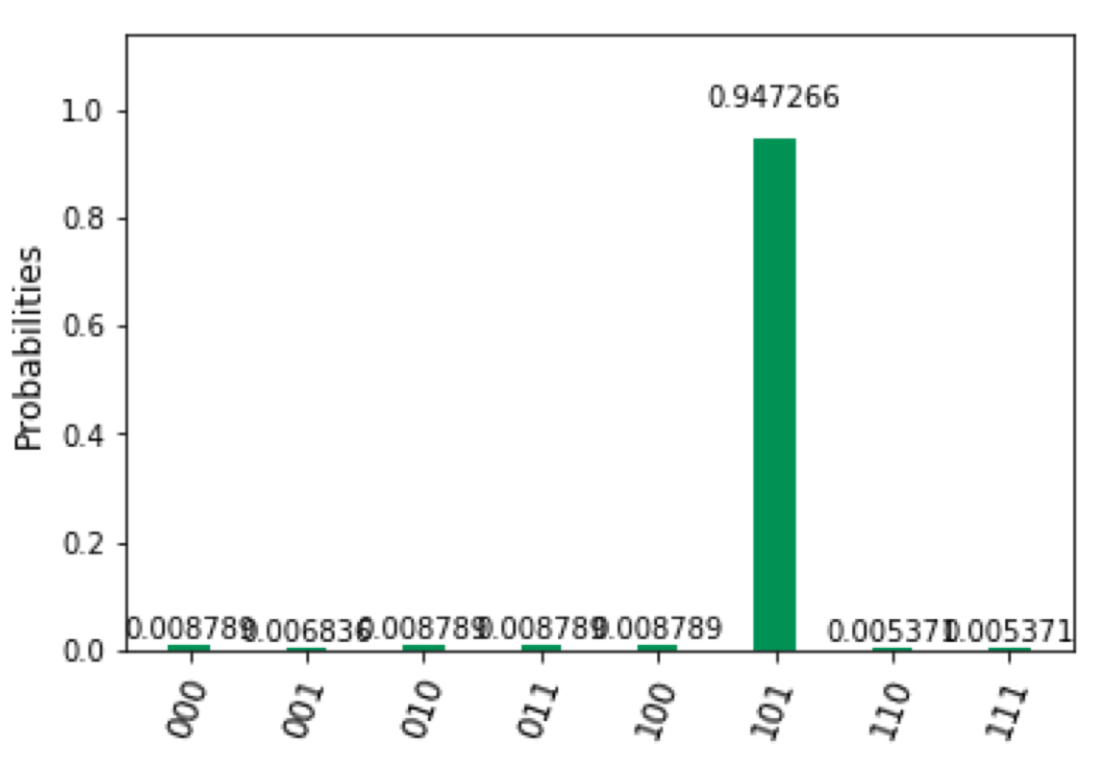
と答えが求まります(答えの1,0,1の部分が高くなる確率分布を得る)。
アルゴリズムの詳細
ここからは、図を提示して詳細を解説します。
といっても振幅増幅を表す行列を作成する部分は問題によらないため、解説は省き、
オラクルを表す行列について解説していきます。
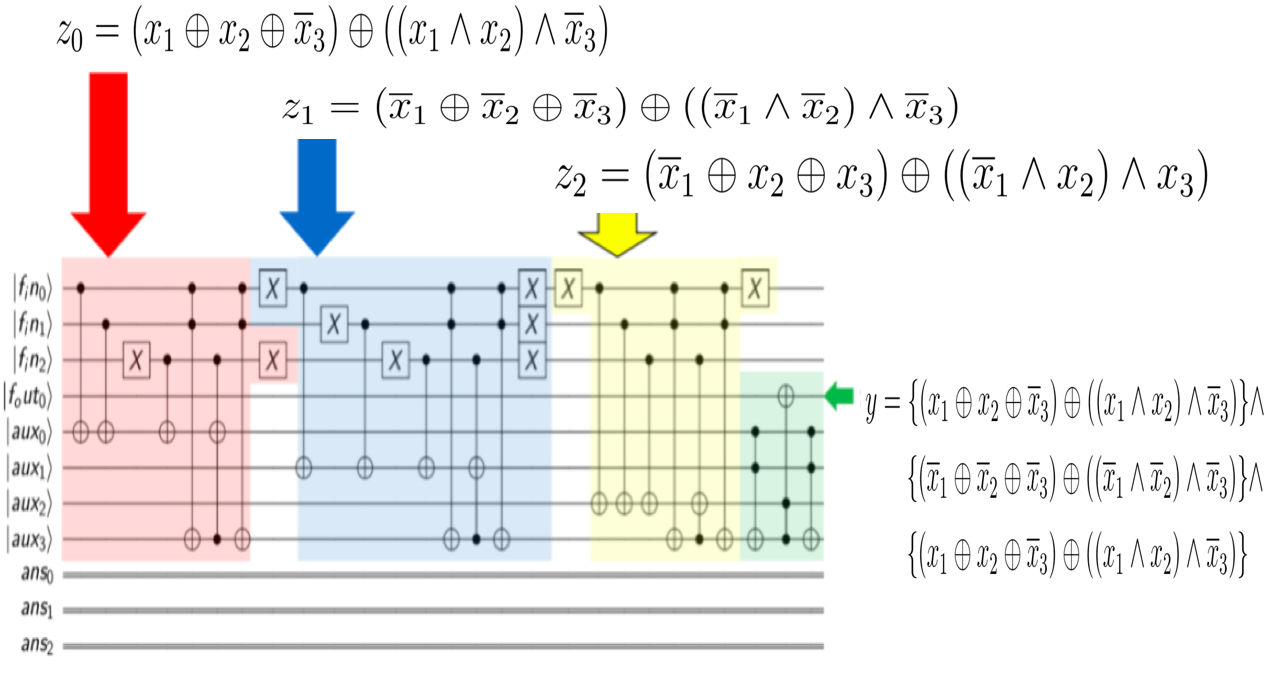
全体の見取り図は以下の通り。
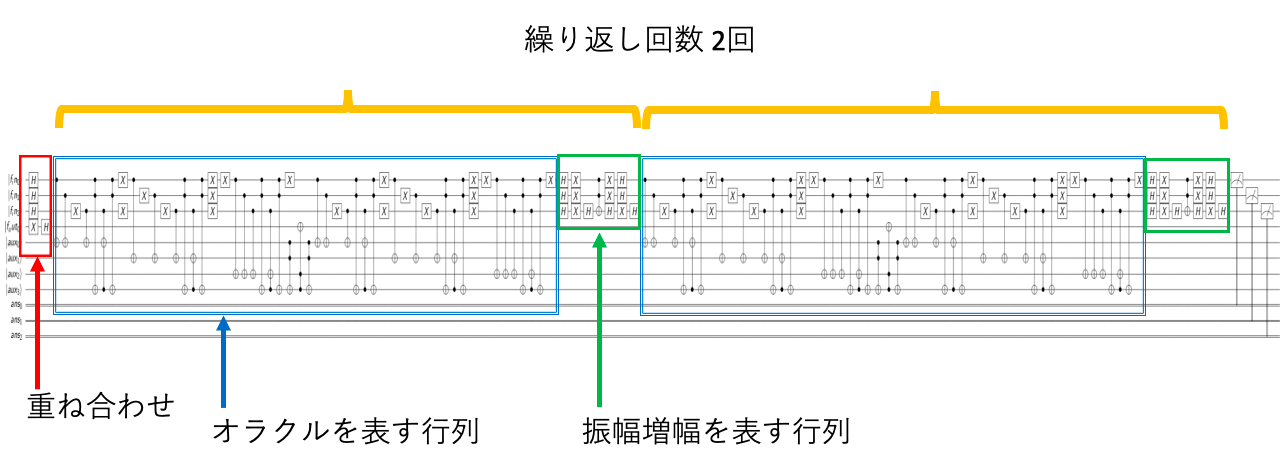
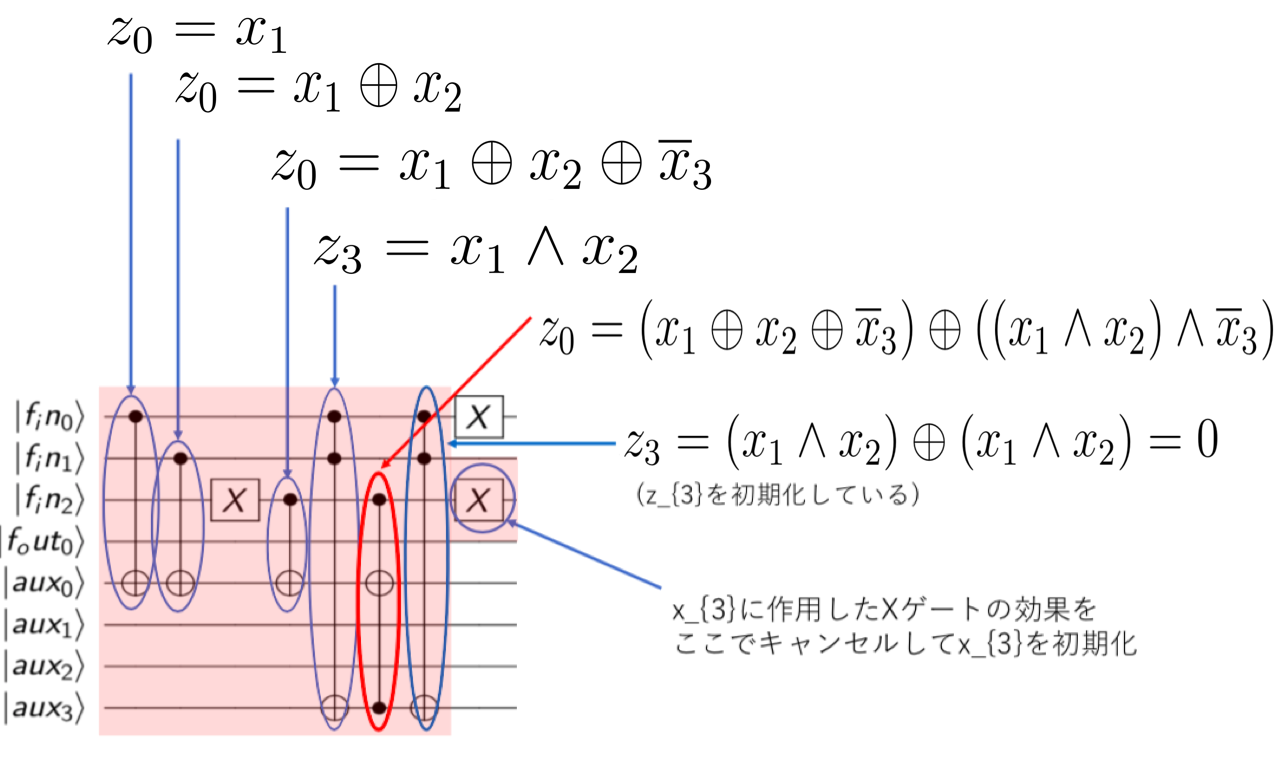
オラクルを表す行列を取り出すと

これは、詳しく見ると同じ演算を2回するところがあるので、
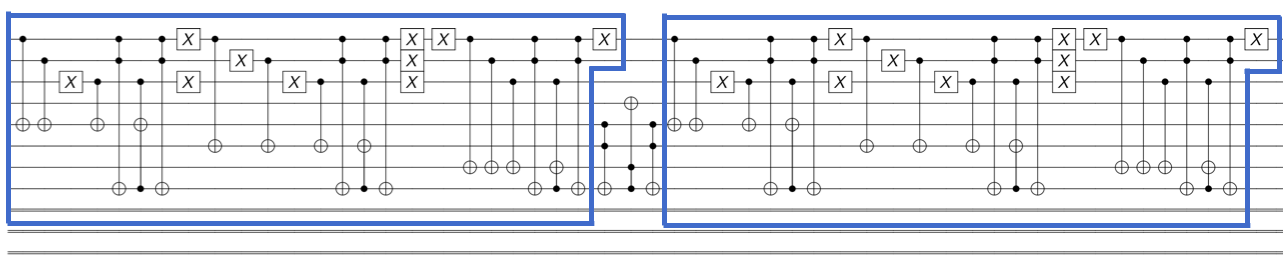
見るべきは、ごく一部です。
これで、オラクルを完成させていることが分かります。
オラクルを表す行列を作用させる後で、
振幅増幅を表す行列を作用させれば、
解の部分のみ振幅を増大させることができます。
後は、これを適切な回数だけ繰り返し、
観測すれば、非常に高い確率で解を得ることができます。
アルゴリズムを1回動かしただけでは、正しい解を得たか完全には分からず
(小さい確率で誤ってしまう)、何度か実行することで、
真に正しい解の部分に密集する確率分布を得ることができます。
以上で、Exactly-1 in 3-SAT 問題に対するグローバーのアルゴリズムを例に取り、
量子アルゴリズムを実際の問題に適用して設計する記事の内容を終わります。
補足
命題の証明を述べておきます。
$a,b,c$をリテラルとする。
$a \vee b \vee c =1$かつ$a,b,c$の中で真$(=1)$は一つのみ
$\Leftrightarrow $
$a \oplus b \oplus c=1$ かつ $a\wedge b \wedge c=0$
である。なぜなら、
$a \oplus b \oplus c=1$ $\Leftrightarrow $1が1つか3つ
$a\wedge b \wedge c=0$ $\Leftrightarrow $少なくとも1つが0
であるから。
次に、
$X = a \oplus b \oplus c$, $Y = a\wedge b \wedge c$とおくと、
$X \oplus Y = 1$は、「$X=1$かつ$Y=0$」 or 「$X=0$かつ$Y=1$」 であることを意味する。ここで、後者の「$X=0$かつ$Y=1$」 が起こらないことを示せばよい。
$Y =1 \Leftrightarrow a\wedge b \wedge c = 1$
$\Leftrightarrow a = b = c = 1$であるが、これと
$X =0 \Leftrightarrow a\oplus b \oplus c = 0$は矛盾する。
以上証明終わり。
参考文献
https://arxiv.org/abs/1708.03684
(An Introduction to Quantum Computing, Without the Physics)