統計を勉強していると必ず正規分布などいくつかの確率分布に出会います。今回はその確率分布の概要と実行できるコードを準備しましたので活用いただければと思います。
はじめに
統計・検定でよく使う以下の確率分布を扱います。
| 確率分布 | 基本形 | ざっくりしたイメージ | よく使うシーン |
|---|---|---|---|
| 標準正規分布 | $z_{\bar{x}}=\frac{x-\mu}{\sigma_{\bar{x}}}$ | 標準化した統計量zが従う分布 | 区間推定 |
| t分布 | $t_{\bar{x}}=\frac{\bar{x}-\mu}{\hat{\sigma_\bar{x}}}$ | t値が従う分布 | 区間推定 |
| $\chi^2$分布 | $\chi^2_{(n)} \equiv \sum_{i=1}^{n}{z_i^2}$ | zの2乗和が従う分布 | 区間推定、クロス集計表の推定 |
| F分布 | $F_{(\nu_1,\nu_2)}=\frac{\frac{\chi^2_{(\nu_1)}}{\nu_1}}{\frac{\chi^2_{(\nu_2)}}{\nu_2}}$ | 2つの母集団から求めた2つの$\chi^2$値、もしくは不偏分散の比が従う分布 | 等分散性の検定や分散分析 |
コードを実行するために
事前に必要なライブラリをインポートしておきます(簡単にコードを実行する環境として無料で使えるGoogleColabが人気です。GoogleColabの使い方について知りたい方は、こちらを確認ください)。
各確率分布のコードを実行する前に、日本語表示用に以下をインストールしておいてください。
# 日本語表記用に事前にインストール
pip install japanize-matplotlib
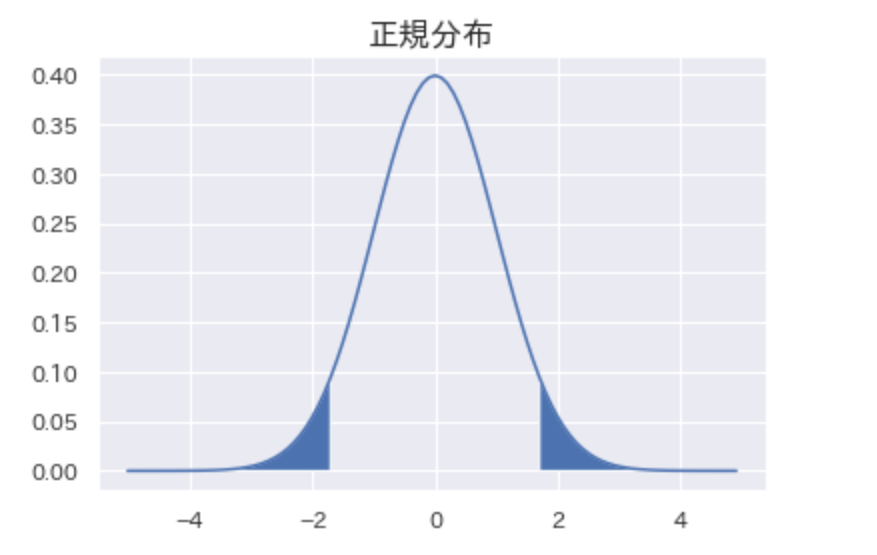
標準正規分布とは
確率分布の基本形です。大標本もしくは母分散がわかっている場合の信頼区間の推定や検定に使います。
標本平均の標準化変量
z_{\bar{x}}=\frac{x-\mu}{\sigma_{\bar{x}}}
標準正規分布の確率密度関数
f(z)=\frac{1}{\sqrt{2\pi}}e^{\frac{-z^2}{2}}
# =====================================================
# 正規分布
# =====================================================
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
import japanize_matplotlib # 日本語化matplotlib
import seaborn as sns
sns.set(font="IPAexGothic") # 日本語フォント設定
# データ
X = np.arange(-5,5,0.1)
# 平均と分散を指定する
a = 0 # 平均
z = 1 # 分散
# 上側、下限を指定
up = norm.ppf(0.95 , loc=0, scale=1)
down = norm.ppf(0.05 , loc=0, scale=1)
# 塗りつぶし範囲を指定
paint = 'b' # u:上限, d:下限, b:上限と下限(デフォルト)
Y = norm.pdf(X,a,z)
# グラフを描画
fig, ax = plt.subplots(1, 1)
ax.plot(X,Y,color='b')
# 塗りつぶし u:上限, d:下限, b:上限と下限(デフォルト)
if paint == 'u':
ax.fill_between( X, Y, 0, where = X > up)
elif paint == 'd':
ax.fill_between( X, Y, 0, where = X < down)
elif paint == 'b':
ax.fill_between( X, Y, 0, where = (X > up) | (X < down))
else:
ax.fill_between( X, Y, 0, where = (X > up) | (X < down))
# グラフの書式指定
plt.title("正規分布", size=16) # タイトル
plt.show()
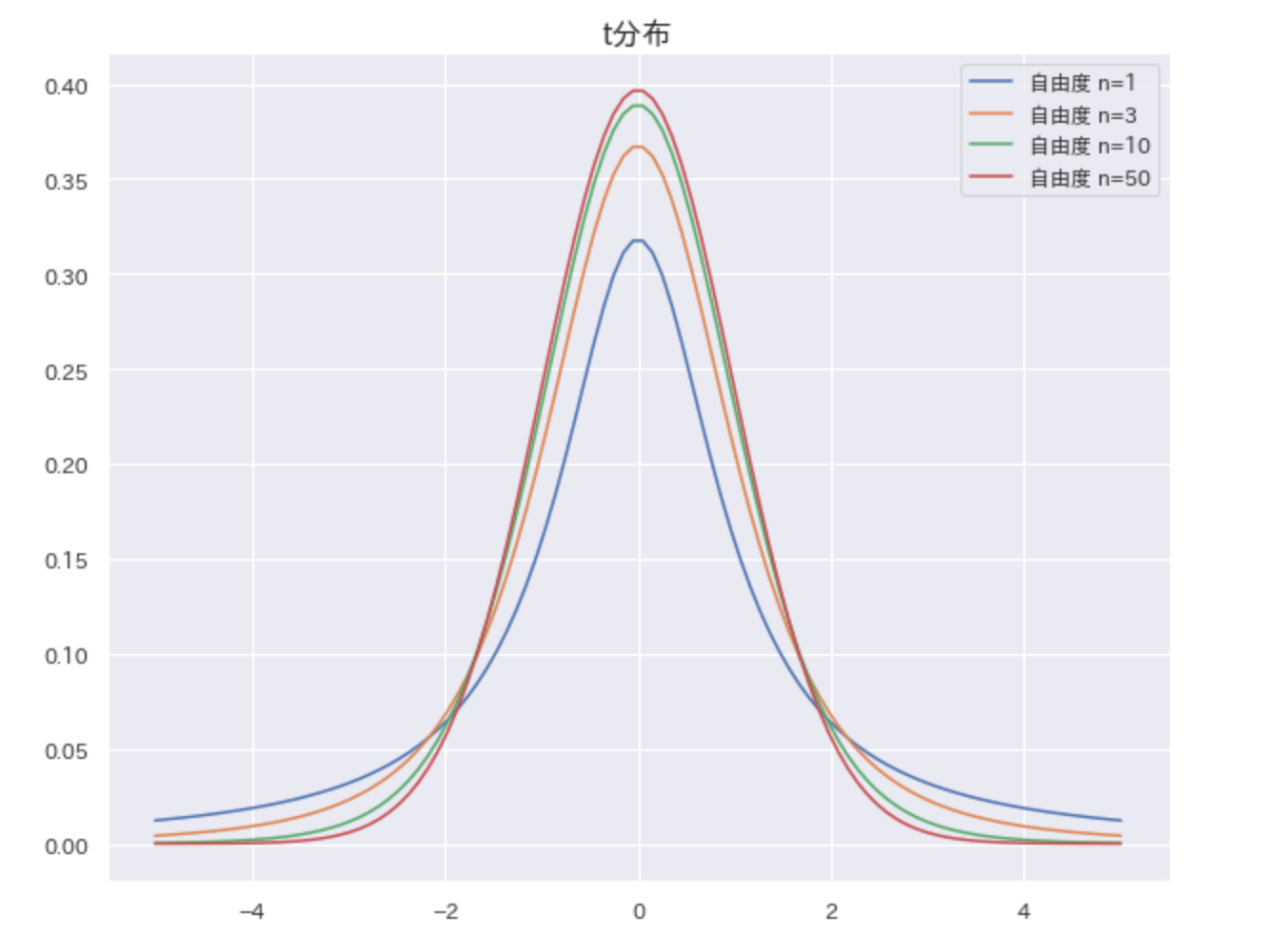
t分布とは
t分布は、名前の通りt値が分布したものです。母分散が未知で小標本の場合の推定・検定に使います。
標本平均$\bar{x_i}$に対するt値は以下の通り、標準化変量zに似た形になっています($\mu$:母平均、s:標本標準偏差、n:標本サイズ)。なお、$\Gamma$は、ガンマ関数(複素数を使った階乗を表す関数で、抽象的なものを求めるときに使う関数)です。
標本平均の準標準化変量
t_{\bar{x}}=\frac{\bar{x}-\mu}{\hat{\sigma_\bar{x}}}=\frac{\bar{x}-\mu}{\frac{\hat{\sigma}}{\sqrt{n}}}=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n-1}}} \\
標準正規分布の確率密度関数
f(t)=\frac{\Gamma(\frac{n}{2})}{\sqrt{(n-1)\pi}\Gamma(\frac{(n-1)}{2})}\Bigl(\frac{1+t^2}{n-1}\Bigr)^{-\frac{n}{2}} \\
# =====================================================
# t分布
# =====================================================
import matplotlib.pyplot as plt
from matplotlib import rcParams
import pandas as pd
import japanize_matplotlib # 日本語化matplotlib
import seaborn as sns
sns.set(font="IPAexGothic") # 日本語フォント設定
# t分布の計算
from scipy.stats import t
import numpy as np
# グラフ設定
fig,ax = plt.subplots(1,1, figsize=(10,8))
# X軸
X = np.linspace(-5,5,100)
# 自由度を指定
n_deg = [1,3,10,50]
# グラフを描画
for i in n_deg:
ax.plot(X, t(i).pdf(X), linestyle='-', label="自由度 n={}".format(i))
# グラフの書式指定
plt.title("t分布", size=16) # タイトル
plt.legend() # 凡例
plt.show()
カイ二乗分布とは
カイ二乗分布は、「$\chi^2$分布」と書き、「かいじじょう」と読みます。
これは、標準化変量Z(要は標準正規分布に従うもの)を2乗和した$\chi^2$値が従う分布です。「zの2乗和は$\chi^2$分布に従う」ということ「$\sum_{i=1}^{n}z^2 ~ \chi^2_{(n)}$」のように書きます。
\\
\chi^2_{(1)} \equiv z^2 = \frac{(x-\mu)^2}{\sigma^2} \\
\chi^2_{(2)} \equiv z_1^2 + z_2^2 = \frac{(x_1-\mu)^2}{\sigma^2}+\frac{(x_2-\mu)^2}{\sigma^2} \\
: \\
\\
\chi^2_{(n)} \equiv \sum_{i=1}^{n}{z_i^2} = \frac{\sum_{i=1}^{n}(x_i-\mu)^2}{\sigma^2} ← 自由度nの\chi^2 値\\
\\
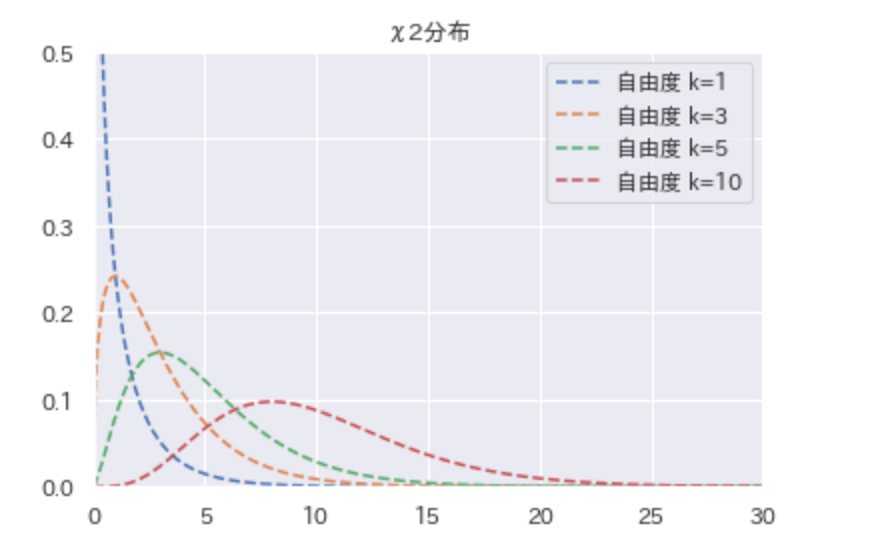
このように$\chi^2$値は、自由度が大きくなるほど、値も大きくなりやすい性質を持っています。
また、自由度が大きくなると正規分布の形に近づくことが知られています。
$\chi^2$分布も正規分布やt分布などと同様に、特定の$\chi^2$値の間確率を確率(分布曲線の面積)を数値積分で計算することができます。特定の上限確率と自由度に対応する$\chi^2$値を、$\chi^2$分布表として統計の巻末などによく掲載してあり、推定・検定などで使います。
# =====================================================
# カイ二乗分布
# =====================================================
import matplotlib.pyplot as plt
from matplotlib import rcParams
import pandas as pd
import japanize_matplotlib # 日本語化matplotlib
import seaborn as sns
sns.set(font="IPAexGothic") # 日本語フォント設定
# カイ二乗分布算出
from scipy.stats import chi2
import numpy as np
# X軸
x = np.linspace(0, 100, 1000)
# 自由度を指定
k_deg = [1, 3, 5, 10]
# グラフを描画
for i in k_deg:
plt.plot(x, chi2.pdf(x, i), linestyle='--', label='自由度 k={}'.format(i))
# グラフの書式指定
plt.title("χ2分布") # タイトル
plt.xlim(0, 30) # X軸範囲
plt.ylim(0, 0.5) # Y軸範囲
plt.legend() # 凡例
plt.show()
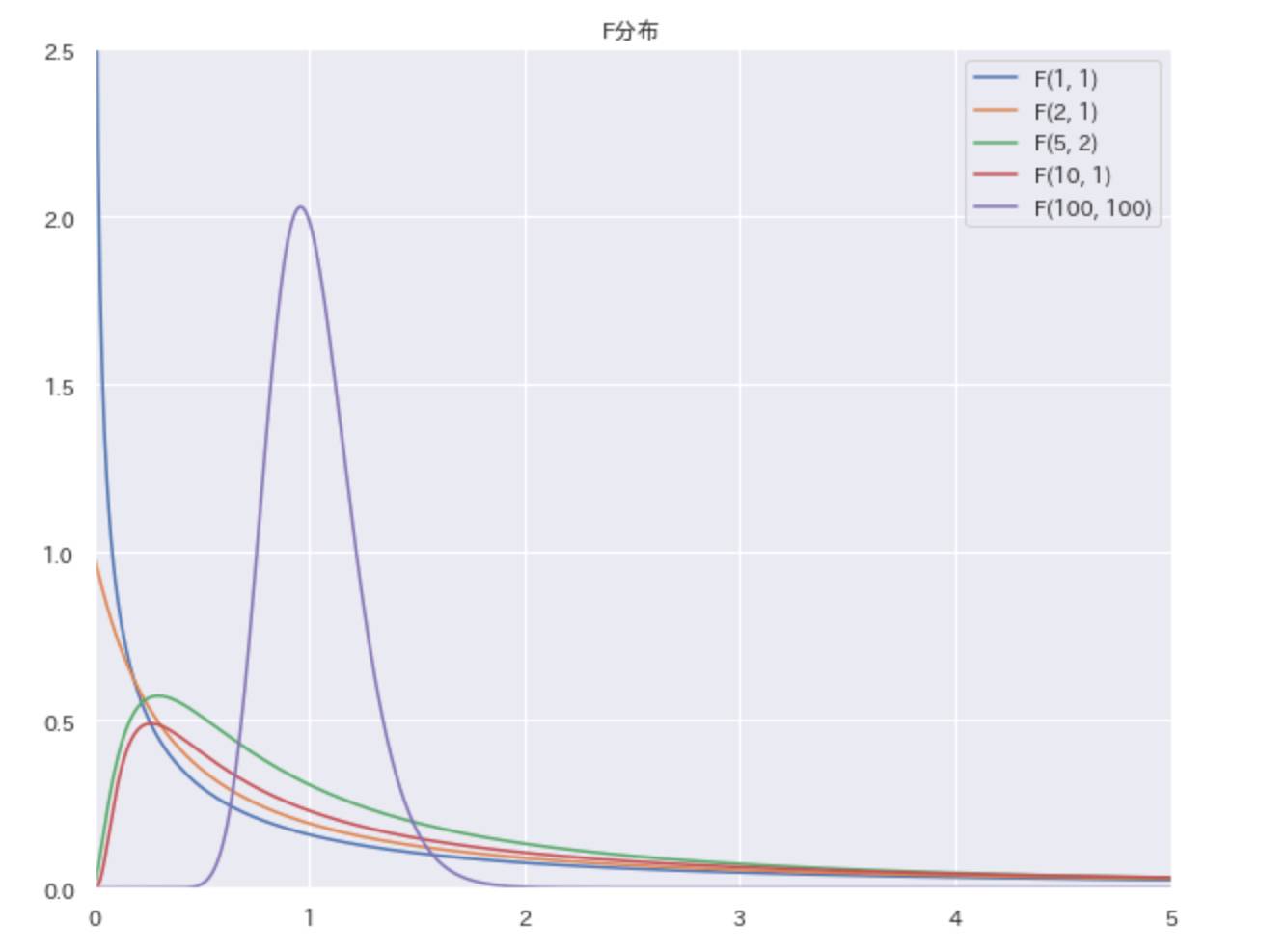
F分布とは
F分布は独立した2つの$\chi^2$値の比であるF値が従う確率分布です。
ただし、$\chi^2$は自由度によって大きく値が変わるので、2つの$\chi^2$値をそれぞれの自由度で割って大きさを補正します。通常、検定時に分布の右裾だけ使えばよいように、分子の値>分母の値 としておきます。
F_{(\nu_1,\nu_2)}=\frac{\frac{\chi^2_{(\nu_1)}}{\nu_1}}{\frac{\chi^2_{(\nu_2)}}{\nu_2}} \\
\\
F分布が2つの母集団から無作為抽出した2つの標本に基づいた統計量が従う分布という性質を利用して、抽出元の2つの母集団の分散が同じかを検定する際などに使われます。
F分布も同様に確率として扱うことが可能です。巻末にF分布表が掲載されていると思いますので確認してみてください。
# =====================================================
# F分布
# =====================================================
import matplotlib.pyplot as plt
from matplotlib import rcParams
from scipy import stats
import numpy as np
import japanize_matplotlib # 日本語化matplotlib
import seaborn as sns
sns.set(font="IPAexGothic") # 日本語フォント設定
# グラフの軸設定
fig,ax = plt.subplots(1,1, figsize=(10,8)) # グラフ
x = np.linspace(0.000001, 10, 1000) # X軸間隔
f_dis = [(1,1),(2,1), (5,2), (10,1), (100,100)] # F(m,n)の自由度設定
# グラフ描画
for i in range(len(f_dis)):
y = stats.f.pdf(x, f_dis[i][0], f_dis[i][1])
ax.plot(x, y, linestyle='-', label=f'F({f_dis[i][0]}, {f_dis[i][1]})')
# グラフの書式指定
plt.title('F分布') # グラフタイトル
plt.xlim(0, 5) # X軸範囲
plt.ylim(0, 2.5) # Y軸範囲
plt.legend() # 凡例
plt.show() # グラフ表示
まとめ
グラフから各統計量の特徴について少し理解が深まったような気がします。
統計に関する記事をいくつか書いていますので、統計に興味がある方、統計勉強中の方、特に統計検定取得を目指している方がいらっしゃったら、ぜひ他の記事も見ていただけるとうれしいです。
- これでわかった! 不偏分散の n-1 !
- 区間推定について(予定)
- 検定について(予定)
- その他検定について(予定) など
参考文献
- 入門統計学 栗原伸一[著]
- 日本統計学会公式認定 統計検定2級対応 統計学基礎 日本統計学会編
本書は筆者たちが勉強した際のメモを、後に学習する方の一助となるようにまとめたものです。誤りや不足、加筆修正すべきところがありましたらぜひご指摘ください。継続してブラッシュアップしていきます。また、様々なモデルの解説書を掲載していますので、興味のある方は、以下のサイトもご参照ください。