統計を勉強していると、不偏分散(平方和を$n-1$で割ったもの)というものがよく登場します。不偏分散は、母平均がわからないときに、標本平均からの差をもとデータのばらつきを計算するものです。その際、標本の数である $n$ で平均化する(標本分散)よりも $n-1$ で平均化する(不偏分散)ほうが、母分散の性質を表すといわれています。
なぜ $n-1$ で割るのかについていろいろな説明の仕方がありましたのでまとめてみました。個人的には、標本の平均から算出した標本平均を使うため、偏差平方和が$(n-1)\sigma^2$になってしまうから、という理解で落ち着きました。すこし長くなってしまいましたが、興味のあるところだけでも見ていただけるとうれしいです。それぞれの詳細は巻末記載の本やURLを参照ください。
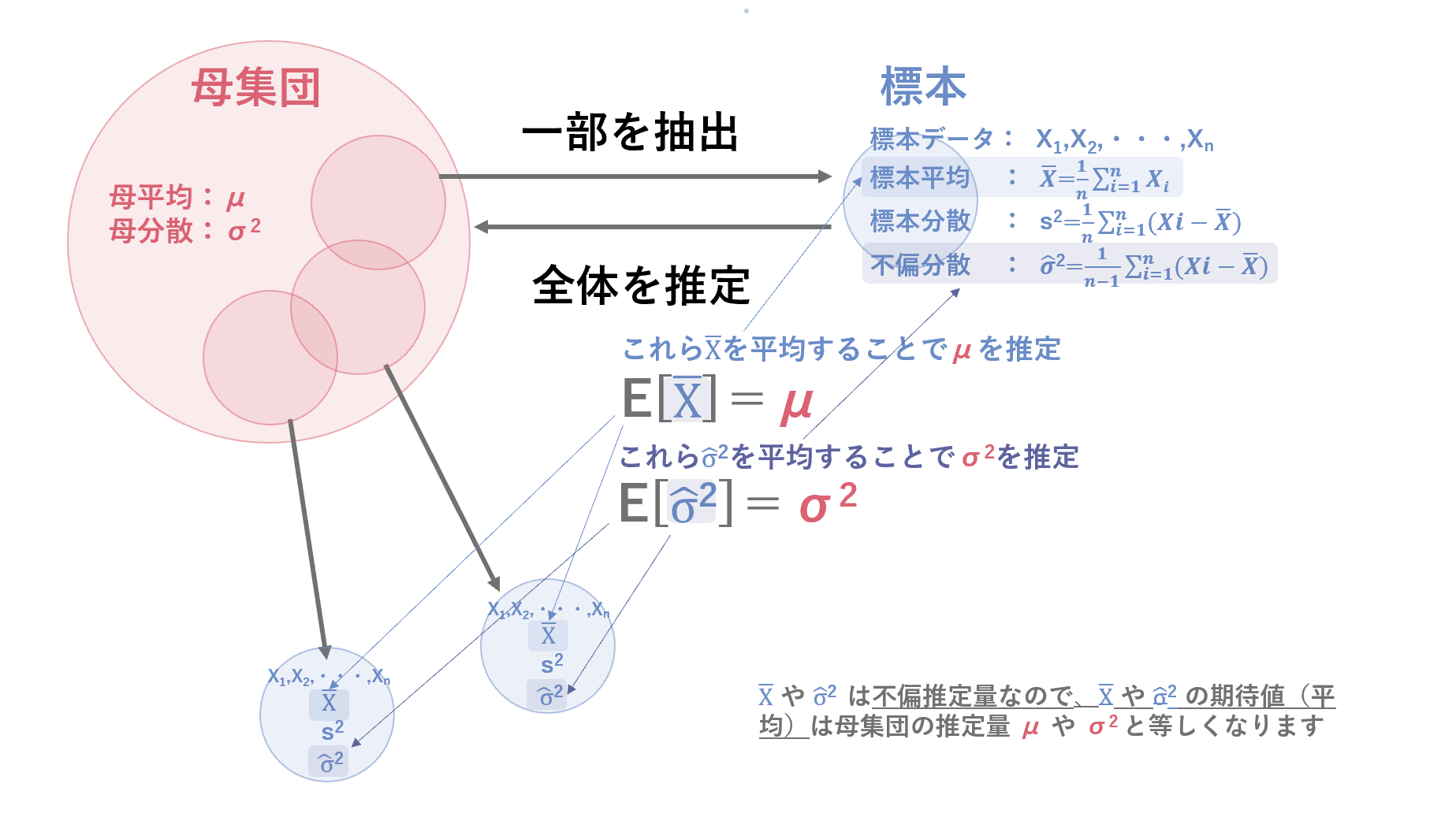
1. 母集団と標本のちがい
- 母集団:調査対象となる数値や属性などを共有する集合全体。
- 標本:母集団と共通の属性をもち、母集団の真部分集合として母集団の推定のためにもうけられたデータの小さな集合体。
1.1 母分散、標本分散、不偏分散
以下の通り、母平均がわかっていれば、母分散は母平均からの偏差とサンプル数 $n$ から直接求められます(ですので不偏分散など持ち込む必要はありません)。ただ、母平均がわかっているケースは稀なので、現実では得られた標本から標本平均を算出し、その偏差から母分散を推定するというアプローチが必要になってきます。その場合、単純に標本サイズ $n$ で割った標本分散よりも、$n-1$ で割った不偏分散のほうが母分散の性質をよく表しているということで不偏分散がよく使われます。
\\
\text{母分散} = \frac{\text{母平均との差の2乗の合計}}{\text{母集団の大きさ}} \\
\\
\text{標本分散} = \frac{\text{標本平均との差の2乗の合計}}{\text{標本の大きさ}} \\
\\
\text{不偏分散} = \frac{\text{標本平均との差の2乗の合計}}{\text{標本の大きさ−1}} \\
\\
多くの場合母集団のサイズは大きいことが多く母集団のすべての値を観測し平均や分散を直接計算することは難しいため、標本のデータを使って母集団の性質を推定します。
2. そもそも不偏推定量ってなに?
標本データからなんらかの統計的な計算をして得た統計量のうち、母集団の性質を偏りなく推定した統計量を不偏推定量と呼びます。具体的には、標本から得られた推定量の期待値が母集団の性質に一致するものです。ちなみに、期待値(確率的な起りやすさを考慮した平均的な値)ではなく、推定量そのものの極限が母集団の性質に一致する推定量は一致推定量と呼ばれます。
-
母平均 $\mu$ の不偏推定量:
標本サイズ $n$ で標本を抽出して算出した標本平均 $\bar{X}= \frac{1}{n}\sum X_i$ は母平均の不偏推定量です。ですので、標本平均の算出を繰り返して、その平均をとれば、母集団の平均を推定できます。 -
母分散 $\sigma^2$ の不偏推定量
標本データ $ X_1,X_2,・・・・,X_n $の $n$ 個のデータと標本平均 $\bar{X}$ の差である $X_iー\bar{X}$の平方和を $n-1$ で割ったものを不偏分散といい、不偏分散は母集団の分散の不偏推定量です。
3. ほんとうに不偏分散の期待値は母分散になるの?
とはいえ本当になるのか、実際に不偏分散の期待値が $\sigma^2$ になるのか計算して確かめてみたいと思います(すでに不偏推定量であるという前提を受け入れられている方は読み飛ばしてください)。
\begin{align}
E(\hat{\sigma^2}) &= E\biggl(\frac{1}{n-1}\sum_{n=1}^{N}\bigl( X_i-\bar{X} \bigr)^2\biggr) \\
&= \frac{1}{n-1}E\biggl( \sum_{n=1}^{N} \Bigl( X_i-\mu+\mu-\bar{X} \Bigr)^2 \biggr) \\
&= \frac{1}{n-1}E\biggl( \sum_{n=1}^{N} \bigl( X_i-\mu \bigr)^2 +2\bigl( \mu-\bar{X} \bigr) \sum_{n=1}^{N} \bigl( X_i -\mu \bigr) + \sum_{n=1}^{N} \bigl( \mu - \bar{X} \bigr)^2 \bigr) \biggr) \\
&= \frac{1}{n-1}E\biggl( \sum_{n=1}^{N} \bigl( X_i-\mu \bigr)^2 -2n\bigl( \bar{X}-\mu \bigr)^2 + n \bigl( \bar{X}-\mu \bigr)^2 \biggr) \\
&= \frac{1}{n-1}\biggl( E \Bigl( \sum_{n=1}^{N} \bigl( X_i-\mu \bigr)^2 \Bigr) -E\Bigl(
n \bigl( \bar{X} - \mu \bigr) ^2 \Bigr) \biggr) \\
&= \frac{1}{n-1} \biggl( n \sigma^2 - n \frac{\sigma^2}{n} \biggr) \\
&= \frac{1}{n-1} \bigl( n-1 \bigr)\sigma^2 \\
\\
&= \sigma^2
\end{align}
真の平均と各データの差の平方和の期待値=母分散
E \Bigl( \bigl( X_i-\mu \bigr)^2 \Bigr) = \sigma^2 \\
4. 不偏分散とはどんなもの?
不偏分散が不偏推定量であるとう前提を受け入れたうえで、ここからは、なぜ $n-1$ で割るとよいのかを深堀し、理解していきたいと思います。ここからは$n-1$だとうまくという説明をいくつかあげていきます。きっとどれかの説明がしっくりきて、不偏分散のイメージをつかめるのではと思います。
4.1 まずはざっくりとした母分散と不偏分散の関係をイメージ
一番ざっくりした理解は、母平均を基準にした偏差を標本数 $n$ で割った期待値は、標本平均を基準にした偏差を $n-1$ で割った期待値と等しいというところからスタートしたいと思います。
\frac{1}{N-1} E \biggl( \bigl( x_i-\bar{x} \bigr)^2 \biggr) = \frac{1}{N}E \biggl( \bigl( x_i-\mu \bigr)^2 \biggr) \\
- 標本分散は母分散を過少評価してしまう
E \Bigl( \bigl( x_i-\bar{x} \bigr)^2 \Bigr) < E \Bigl( \bigl( x_i-\mu \bigr)^2 \Bigr)
母分散、標本分散、不偏分散の分子は偏差平方和ですが、この偏差を算出する際、標本分散や不偏分散は母平均からの差ではなく標本平均(データから算出した標本に寄った値)からの差を使っています。そのため偏差平方和が想定より小さくなり、$n$で割った標本分散では母分散を過少評価してしまいます。
不偏分散は、分母を $n$ から $n-1$ に少し小さくすることで、都合よく小さくしてしまった分をちょっと大きく戻すようなイメージです。
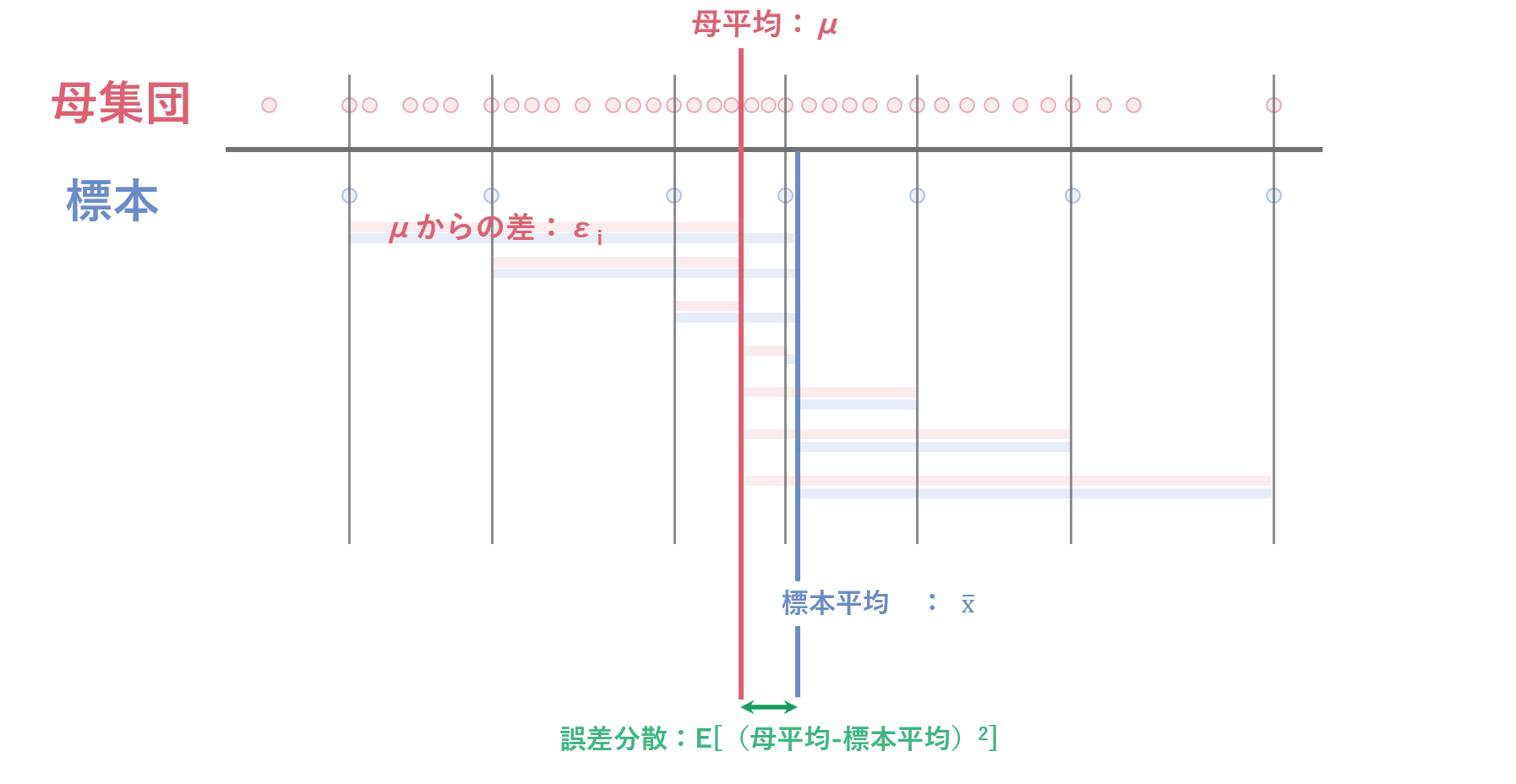
4.2 標本平均自体にもばらつきがあるから、という説明
標本分散や不偏分散の算出に使っている標本平均はサンプルに従ってバラつきをもつ量になります。したがって、分散(データ自体のばらつき)を考える場合、その平均自体のバラつき自体も考慮する必要があります。
\begin{align}
\sigma^2 &= \frac{1}{n}\sum_{i=1}^{n}\bigl( x_i-\mu \bigr)^2 \\
&= \frac{1}{n}\sum_{i=1}^{n}\bigl( x_i - E (\bar{x}) \bigr)^2 + \frac{\sigma^2}{n} \\
\\
∴ \sigma^2 - \frac{\sigma^2}{n} &= \frac{1}{n}\sum_{i=1}^{n}\bigl( x_i - E(\bar{x}) \bigr)^2 \\
\sigma^2 &= E\biggl(\frac{1}{n-1} \sum_{i=1}^{n}\bigl( x_i - \bar{x} \bigr)^2 \biggr) = E\Bigl( \hat{\sigma^2} \Bigr)\\
\end{align}
標本平均と真の平均の差の二乗和の期待=誤差分散(標準誤差$^2$)
E \Bigl( \bigl( \bar{X}-\mu \bigr)^2 \Bigr) = \frac{\sigma^2 }{n} \\
誤差分散は、標本平均$\bar{X}$の分散をあらわす統計量
$n$が十分に大きければゼロに近づき、$n$が小さい場合には特に考慮が必要です。
4.3 母平均からの差と標本平均の関係を使った説明
\begin{align}
\epsilon_i &= x_i-\mu とおくと E \bigl( \epsilon_i \bigr) = 0、V \bigl( \epsilon_i \bigr) = \sigma^2 \\
i &\neq jで \epsilon_i と \epsilon_j は独立 \\
\bar{\epsilon}&=\frac{1}{N} \sum \epsilon_i とすると \bar{x} = \bar{\epsilon} + \mu \\
\\
E \biggl( \bigl( x_i-\bar{x} \bigr)^2 \biggr) &=
E \biggl( \Bigl( \bigl( \mu+\epsilon_i \bigr)-\bigl( \mu+\bar{\epsilon} \bigr) \Bigr)^2 \biggr) \\
&= E \biggl( \bigl( \epsilon_i-\bar{\epsilon} \bigr)^2 \biggr) \\
&= E \biggl( \bigl( \epsilon_i-\frac{1}{N}\sum\epsilon_j \bigr)^2 \biggr) \\
&= E \biggl( \Bigl( \bigl(1-\frac{1}{N} \bigr) \epsilon_i-\frac{1}{n}\sum_{j\neq i}\epsilon_j \Bigr)^2 \biggr) \\
&= E \biggl( \bigl(\frac{N-1}{N} \bigr)^2 \epsilon_i^2 + \sum_{j\neq i}\frac{1}{N^2} \epsilon_j^2 \biggr) \\
&= \bigl( \frac{N-1}{N} \bigr)^2 E \bigl( \epsilon_i^2 \bigr) + \frac{1}{N^2}\sum_{j\neq i}E \bigl( \epsilon_j^2 \bigr) \\
&= \Bigl( \bigl( \frac{N-1}{N} \bigr)^2 + \bigl( N-1 \bigr) × \frac{1}{N^2} \Bigr) \sigma^2 \\
&= \frac{N-1}{N}\sigma^2 \\
∴ \frac{1}{N-1}E \biggl( \bigl( x_i-\bar{x} \bigr)^2 \biggr)&= \frac{1}{N}\sigma^2 = \frac{1}{N}E \biggl( \bigl( x_i-\mu \bigr)^2 \biggr)
\end{align}
式変形における補足
$i≠j$で $\epsilon_i$と$\epsilon_j$が独立なとき、$i≠j$で $E[\epsilon_i×\epsilon_j]=E[\epsilon_i]×E[\epsilon_j]=0$
$V[\epsilon_i]=E[\epsilon_i^2]-E[\epsilon_i]^2=\sigma^2$ から $E[\epsilon_i^2]=V[ \epsilon_i]-E[\epsilon_i]^2 =\sigma^2-0=\sigma^2$
4.4 自由度を使ったイメージ
- 自由度は、自由に動かせる標本データ(変数)の数を意味しています。
- 分散は、偏差平方和÷自由度と表現できます。
- 不偏分散のデータの自由度は、標本平均が既に算出されているので、自由になるデータの数は$n-1$です(偏差の総和はゼロという束縛条件)。ですので、不偏分散の自由度は $n-1$ です。
例)3つのデータA=100、B=98、C=102があった場合、平均=100となり、Aが100、Bが98とわかった場合、Cは102であると自動的に決まってしまいCは自由に決めることができません。
4.5 ベクトルを使った説明
前章の自由度を使ったイメージでは、自由度が1減ったというイメージはできても、本当に期待値が母分散になるの?という点は直接的には表現できていません。自由度が $n-1$ の場合の不偏性についてベクトルの次元を使って深堀りしていきたいと思います。
ベクトルで考える
$E[\sum_{i=1}^{n}\bigl( X_i - \bar{X} \bigr)^2]=(n-1)\sigma^2$ となることをベクトル$X$(各データ$X_i$を要素とするベクトル)とベクトル$\tilde{X}$ (各データ$X_i$と平均)$\bar{X}$の差を要素とするベクトル)を使って考えていきます。
\begin{eqnarray}
X=\left(
\begin{array}{X}
X_{1} \\
X_{2} \\
: \\
X_{n} \\
\end{array}
\right)
,
\tilde{X}=\left(
\begin{array}{X~}
X_{1}-\bar{X} \\
X_{2}-\bar{X} \\
: \\
X_{n}-\bar{X} \\
\end{array}
\right)
\end{eqnarray}
\\
ベクトルの長さは各要素の2乗の和となることから、$|| \tilde{X} ||^2= \bigl( X_1-\bar{X} \bigr)^2 + \bigl( X_2-\bar{X} \bigr)^2 + ・・・ + \bigl( X_n-\bar{X} \bigr)^2= \sum_{i=1}^{n}\bigl( X_i-\bar{X} \bigr)^2$ と求められます。したがって、$E \biggl( \sum_{i=1}^{n}\bigl( X_i - \bar{X} \bigr)^2 \biggr) = E \biggl( || \tilde{X} ||^2 \biggr) $とベクトルの長さを使って考えることができます。
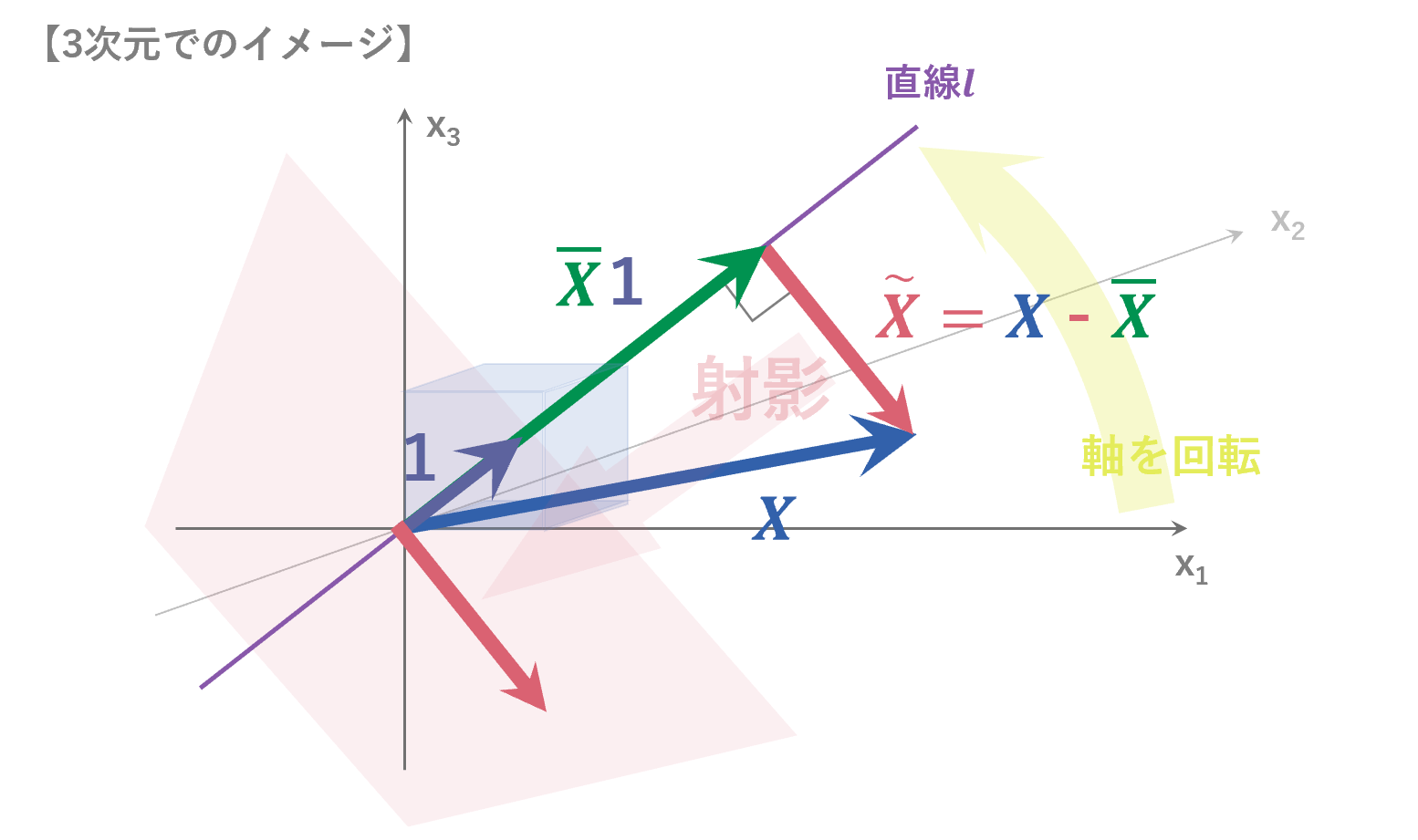
ここで $\tilde{X}$ がどんなベクトルかを考えると、以下の図のようになります。
$\vec{1}$を各要素が1の方向で大きさが1のベクトルとすると、
\tilde{X}・\bar{X}\vec{1}=0
$\tilde{X}$は、$\vec{1}$を通る直線$l$と$\bar{X}\vec{1}$で直交する性質(どんな$X$でもその平均$\bar{X}$との差をとった$\tilde{X}$は、直線$l$と直交するという性質)から、$\tilde{X}$(=$X$ー$\bar{X}$:標本データ$X$から標本平均$\bar{X}$を引くことこと)は、$X$の、$\vec{1}$に垂直な面への射影だと考えることができます($\vec{1}$ に垂直な面に射影するということは、$\vec{1}$ 方向の成分を考えなくてよくなったということです)。
ここまでで射影によってある成分を考慮せずにすむ特性があることはわかりました。しかし、$\vec{1}$の方向では扱いにくいため、基底を変更して新たな基底の第一成分をなくすことを考えます。新たな座標系を考えるため、以下のような回転行列を考えます。
\begin{eqnarray}
回転行列R=\left(
\begin{array}{X}
v_{1} \\
v_{2} \\
: \\
v_{n} \\
\end{array}
\right)=(a_{ij})_{ij}
,
ただし、ベクトルv_{1}=\left(
\begin{array}{X}
\frac{1}{\sqrt{n}} , \frac{1}{\sqrt{n}} ,... , \frac{1}{\sqrt{n}}
\end{array}
\right) \\
\end{eqnarray}
回転行列$R$は、正規直交行列であるという性質より、任意の$i$に対して、$\sum_{j}a_{ij}=0$ (直交より)、$\sum_{j}a_{ij}^2=1$(正規性より)となります。
ここで新たな座標系での$R\tilde{X}$という行列について平均$E$と分散$V$を確認しておきます。
\begin{eqnarray}
R\tilde{X}&=\left(
\begin{array}{X}
v_{1}\tilde{X} \\
v_{2}\tilde{X} \\
: \\
v_{n}\tilde{X} \\
\end{array}
\right)=\left(
\begin{array}{X2}
0 \\
v_{2}\tilde{X} \\
: \\
v_{n}\tilde{X} \\
\end{array}
\right)
\end{eqnarray}
\begin{align}
v_i \tilde{X} &= a_{i1} \bigl( X_1 - \bar{X} \bigr) + a_{i2} \bigl( X_2 - \bar{X} \bigr) +...+ a_{in} \bigl( X_n - \bar{X} \bigr) \\
\\
E \Bigl( v_i \tilde{X} \Bigr) &= E \Bigl( a_{i1} \bigl( X_1 - \bar{X} \bigr) + a_{i2} \bigl( X_2 - \bar{X} \bigr) +...+ a_{in} \bigl( X_n - \bar{X} \bigr) \Bigr) \\
&= a_{i1} E(X_1 - \bar{X}) + a_{i2} E(X_2 - \bar{X}) +...+ a_{in} E(X_n - \bar{X}) \\
&= a_{i1} ×0 + a_{i2} ×0 +...+ a_{in} ×0 \\
&= 0 \\
\\
V \Bigl( v_i \tilde{X} \Bigr) &= V \Bigl( a_{i1} \bigl( X_1 - \bar{X} \bigr) + a_{i2} \bigl( X_2 - \bar{X} \bigr) +...+ a_{in} \bigl( X_n - \bar{X} \bigr) \Bigr) \\
&= a_{i1}^2 V\bigl(X_1\bigr) + a_{i2}^2 V\bigl(X_2\bigr) + ... + a_{i1}^2 V\bigl(X_1\bigr) \\
&= a_{i1}^2 \sigma^2 + a_{i2}^2 \sigma^2 + ... + a_{i1}^2 \sigma^2 \\
&= \bigl( a_{i1}^2 + a_{i2}^2 + + a_{in}^2 \bigr) \sigma^2 \\
&= \sigma^2 \\
\end{align}
すると、以下のようにベクトルの距離を使って、偏差平方和が$(n-1)\sigma^2$となることがわかります。
\begin{align}
E \Bigl( \sum_{i=1}^{n} \bigl( X_i - \bar{X} \bigr)^2 \Bigr) &= E \Bigl( || \tilde{X} ||^2 \Bigr) \\
&= E \Bigl( \sum_{i=1}^{n} \bigl( v_i \tilde{X} \bigr)^2 \Bigr) \\
&= \sum_{i=2}^{n} E \Bigl( v_i \tilde{X} \Bigr)^2 \\
&= \sum_{i=2}^{n} \biggl( V\bigl( v_i \tilde{X} \bigr) + \Bigl(E\bigl( v_i \tilde{X} \bigr)\Bigr)^2 \biggr) \\
&= \sum_{i=2}^{n} V\bigl( v_i \tilde{X} \bigr) + \sum_{i=2}^{n} \Bigl( E\bigl( v_i \tilde{X} \bigr) \Bigr)^2 \\
&= (n-1)\sigma^2 \\
\end{align}
5 まとめ
統計検定の勉強をする中でベクトルでの解説に出会い感動しました。いろいろな方向からの解説をみることで、不偏分散の「n-1」がなんとなくなじんできたように思います。
推定量の不偏性は理論的に重要な概念とされていますが、推定量が必ずもつべき性質ではなく(一致推定量であるが不偏推定量でないものや、不偏推定量が存在しないものもあり)、推定量の不偏性を絶対視する必要はないようです。うまくつきあっていけたらいいですね。
【参考文献、サイト】
- 4.2章:入門統計学 栗原伸一[著]
- 4.3章:Youtube AIcia Solid Project https://www.youtube.com/watch?v=x4q4Uaihws4
- 4.5章:Youtube AIcia Solid Project https://www.youtube.com/watch?v=k9r_qQbZS5Q
本書は筆者たちが勉強した際のメモを、後に学習する方の一助となるようにまとめたものです。誤りや不足、加筆修正すべきところがありましたらぜひご指摘ください。継続してブラッシュアップしていきます。また、様々なモデルの解説書を掲載していますので、興味のある方は、以下のサイトもご参照ください。