統計検定の勉強をしていると、区間推定というものが出てきます。そもそも何をやっているのか、まとめていきたいと思います。
1. 区間推定ってそもそも何?
今回扱う区間推定は、推測統計学の最も基本的な手法で、標本から母集団を幅をもって推測するものです。推測統計学とは、ベイズ統計とちがい、母集団分布のパラメータが何らかの固定された値であると考えます。その知りたい母集団を今手元にある標本から推測するというアプローチです。
区間推定を使いこなせるようになると、例えば、小6男子全体の身長の平均をある地域のデータから幅を持って、95%の信頼区間で150㎝~155㎝の間に入るなどと推定できるようになります。
1.1 区間推定の基本
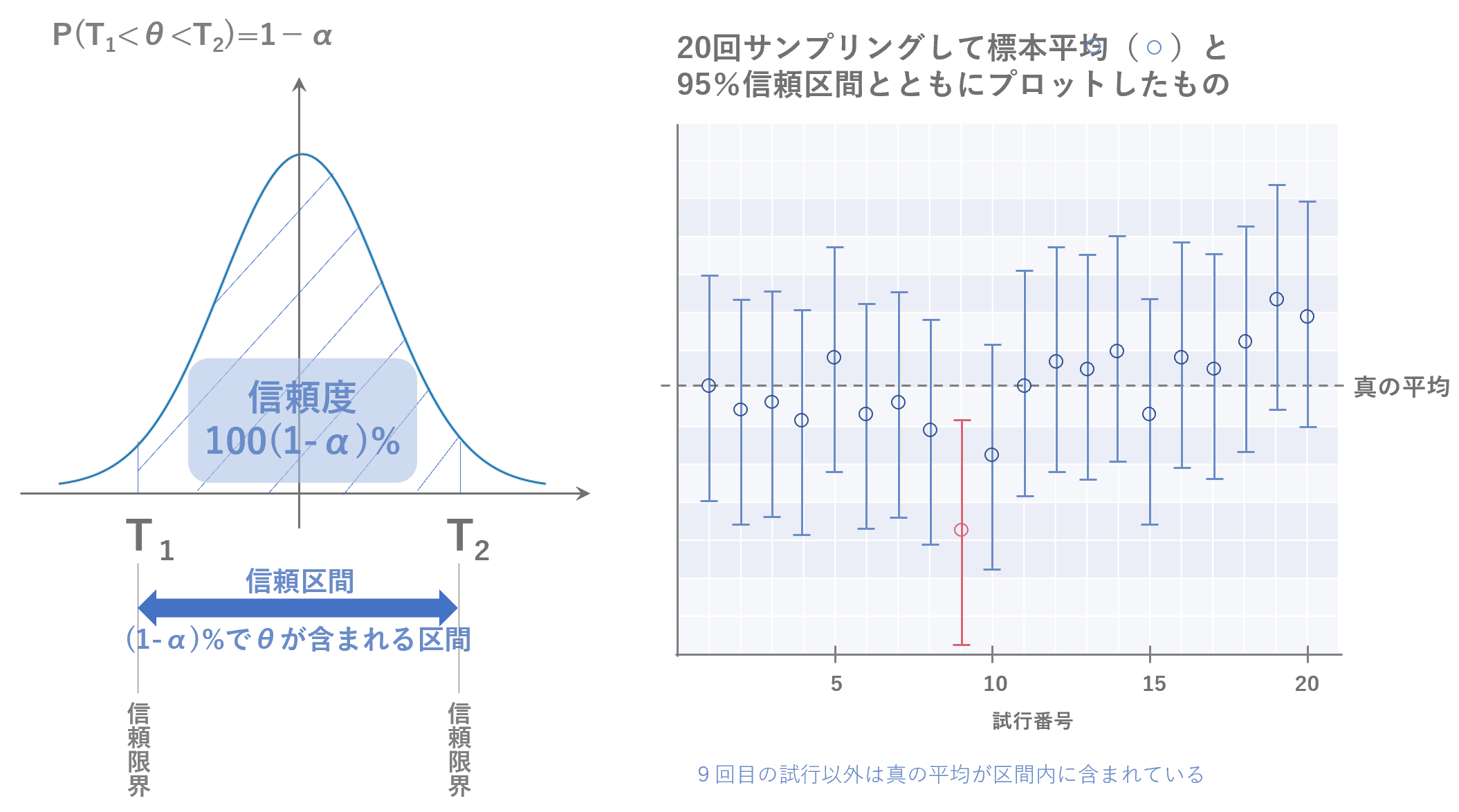
区間推定では、未知の母数$\theta$を1つの推定量で推定するのではなく、一定の確率($100(1-\alpha)$%)で2つの推定量($T_1,T_2$)の間の区間に$\theta$が含まれるかどうかで考えます。『 $P(T_1<\theta<T_2)=(1-\alpha)$ 』 のように表現し、区間$(T_1 , T_2)$を$\theta$の信頼区間、$100(1-\alpha)$%をこの区間の信頼度(または信頼係数)、$T_1$ 、 $T_2$を信頼限界と呼びます。
95%信頼区間の意味
標本平均$\bar{x}$を1つ算出したときに、その標本平均$\bar{x}$が95%の確率で$\mu$付近に存在するというのは直接的にわかりやすいですが、$\mu$の信頼区間の解釈としては、算出した標本平均$\bar{x}$の近くに$\mu$がいる確率が95%となります。例えば、95%の信頼区間の場合、100回標本をとってきて、95回は近くに$\mu$があり、残りの5回は近くに$\mu$がないという意味です。
2. 区間推定って実際にはどんなことができるの?
区間推定でどのような推定ができるのかの具体的な例をあげていきたいと思います。平均や母比率、分散自体の推定や、2つの標本の差に対する推定といった代表的なものを扱います。どうしてこのような式で求められるのかなど疑問に思うものがあれば、後半に意味などを記載していますので、興味のある方はぜひ確認してみてください。
[補足:以下の信頼区間算出の中で使われている記号の意味]
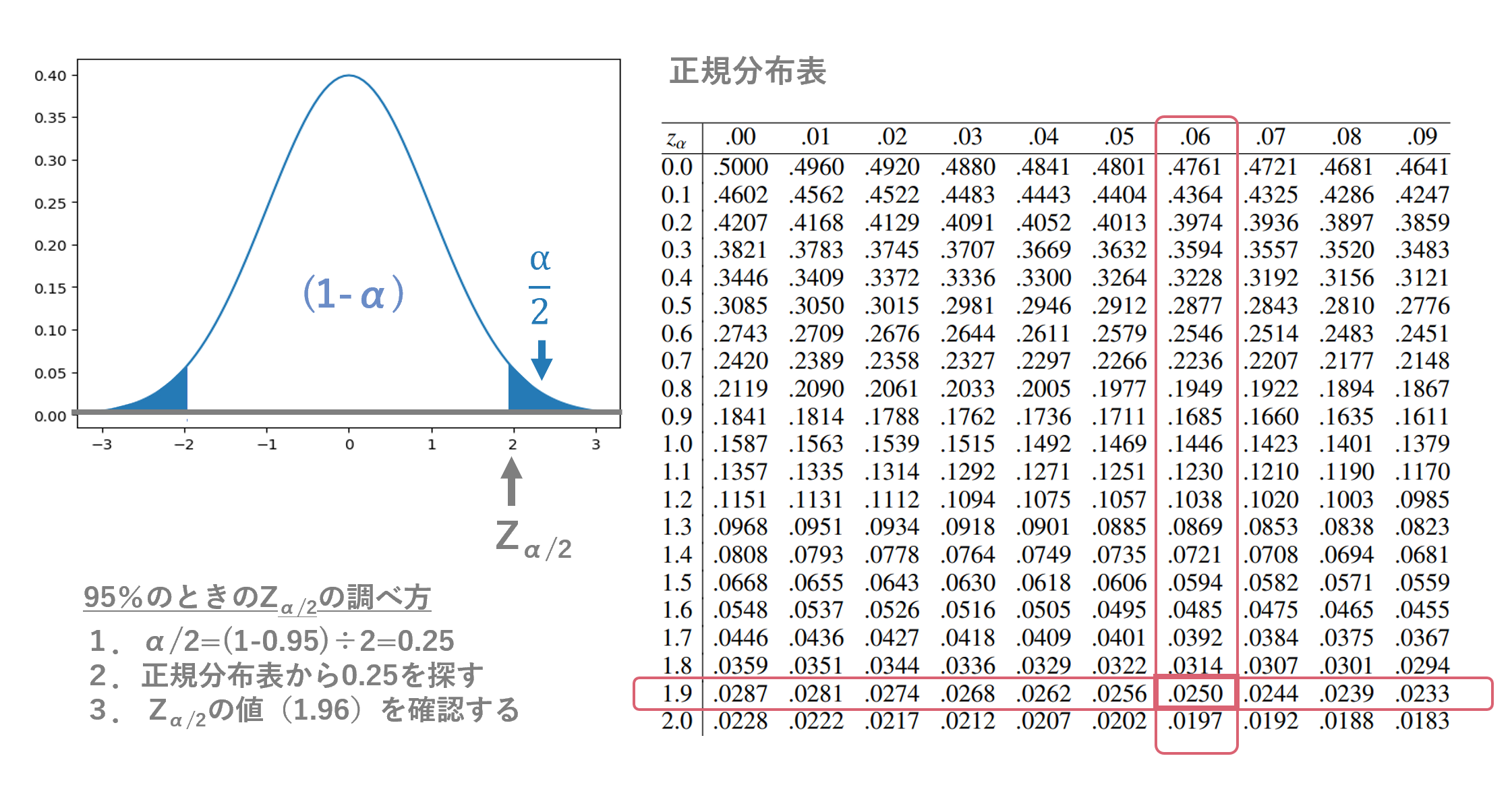
$Z_\frac{\alpha}{2}$:標準正規にしたがう確率変数$X$が$P(X>Z_\frac{α}{2})=\frac{α}{2}$となるような値
$t_\frac{\alpha}{2}(n-1)$:自由度$(n-1)$のt分布に従う確率変数$X$が$P(X>t_\frac{α}{2})=\frac{α}{2}$となるような値
$\chi^2_\frac{\alpha}{2}(n-1)$:自由度$(n-1)$の$\chi^2_\frac{\alpha}{2}$分布に従う確率変数$X$が$P(X>\chi^2_\frac{α}{2})=\frac{α}{2}$となるような値
2.1 平均の区間推定
まずは、母平均の信頼区間や、2つの標本の平均の差の信頼区間を求めます。母分散がわかっているとき/わからないとき、標本サイズが大きいとき/小さいときの条件によって信頼区間の計算方法が変わります(標本サイズが約30以上のとき大標本)。母分散がわからないときは、母分散の代わりに標本から得た不偏分散$u^2=\frac{1}{n-1}\sum{(x_i-\bar{x})^2}$を使用します。また、標本サイズが小さいときは、標準正規分布のかわりに自由度(n-1)のt分布を使用します(t分布自体の説明については省略しますので気になる方はこちらの記事で説明していますので参考にしてください。)
)。
平均μの100(1-α)%の信頼区間:
| 分散$\sigma^2$ | 標本 | 区間 |
|---|---|---|
| 既知 | - | $\Bigl(\bar{x}-Z_\frac{\alpha}{2}\sqrt{\frac{\sigma^2}{n}} , \bar{x}+Z_\frac{\alpha}{2}\sqrt{\frac{\sigma^2}{n}} \Bigr)$ |
| 未知 | 大標本 | $\Bigl(\bar{x}-Z_\frac{\alpha}{2}\sqrt{\frac{u^2}{n}} , \bar{x}+Z_\frac{\alpha}{2}\sqrt{\frac{u^2}{n}} \Bigr)$ |
| 未知 | 小標本 | $\Bigl(\bar{x}-t_\frac{\alpha}{2}(n-1)\sqrt{\frac{u^2}{n}} , \bar{x}+t_\frac{\alpha}{2}(n-1)\sqrt{\frac{u^2}{n}}\Bigr)$ |
2つの平均μ1、μ2の差(μ1-μ2)の100(1-α)%信頼区間:
| 分散 $\sigma_1^2$、$\sigma_2^2$ | 標本 | 区間 |
|---|---|---|
| 既知 | - | $\Bigl(\bar{x_1}-\bar{x_2}-Z_\frac{\alpha}{2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}} , \bar{x_1}-\bar{x_2}+Z_\frac{\alpha}{2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\Bigr)$ |
| 未知 | 大標本 | $\Bigl(\bar{x_1}-\bar{x_2}-Z_\frac{\alpha}{2}\sqrt{\frac{u_1^2}{n_1}+\frac{u_2^2}{n_2}} , \bar{x_1}-\bar{x_2}+Z_\frac{\alpha}{2}\sqrt{\frac{u_1^2}{n_1}+\frac{u_2^2}{n_2}}\Bigr)$ |
| 未知 $(\sigma_1^2=\sigma_2^2)$ | 小標本 | $\Bigl(\bar{x_1}-\bar{x_2}-t_\frac{\alpha}{2}(n_1+n_2-2)\sqrt{\frac{(n_1-1)u_1^2+(n_2-1)u_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}$ , $\bar{x_1}-\bar{x_2}+t_\frac{\alpha}{2}(n_1+n_2-2)\sqrt{\frac{(n_1-1)u_1^2+(n_2-1)u_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}\Bigr)$ |
※$u_1^2$、$u_2^2$は、$\sigma_1^2$、$\sigma_2^2$の標本不偏分散
[差の検定における分散部分に関する補足]
大標本の場合
$n$が大きいため(不偏分散の一致性より)不偏分散をそのまま分散として扱っています。
$V[\bar{x_1}-\bar{x_2}]=V[\bar{x_1}]+V[\bar{x_2}]$より単純に各分散の和を分散としています。
小標本の場合(プールした分散)
$n$が小さいため不偏分散をそのまま分散と扱うのははばかられます。
標準化変量$Z=\frac{\bar{x_1}-\bar{x_2}-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma^2}{n_1}+\frac{\sigma^2}{n_2}}}$
$\chi^2_1(n_1-1)=\frac{(n_1-1)u_1^2}{\sigma^2}$、$\chi^2_2(n_2-1)=\frac{(n_2-1)u_2^2}{\sigma^2}$より$\chi^2_1(n_1-1)+\chi^2_2(n_2-1)=\frac{(n_1-1)u_1^2+(n_2-1)u_2^2}{\sigma^2} ~\chi^2(n_1+n_2-2)$
$X~N(0,1)$、$Y~\chi^2(m)$のとき、$\frac{X}{\sqrt{\frac{Y}{m}}}~t(m)$ (t分布の定義)より
$t=\frac{Z}{\sqrt{\frac{\chi^2}{自由度}}}=\frac{\bar{x_1}-\bar{x_2}-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma^2}{n_1}+\frac{\sigma^2}{n_2}}}・\frac{1}{\sqrt{\frac{(n_1-1)u_1^2+(n_2-1)u_2^2}{\sigma^2(n_1+n_2-2)}}}=\frac{\bar{x_1}-\bar{x_2}-(\mu_1-\mu_2)}{\sqrt{\frac{(n_1-1)u_1^2+(n_2-1)u_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}}$
2.2 母比率の区間推定
母比率$p$や母比率の差$p_1-p_2$の信頼区間は、以下のように求めることができます(いずれのケースも大標本)。
母比率pの100(1-α)%の信頼区間:
\Bigl(\hat{p}-Z_\frac{\alpha}{2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} , \hat{p}+Z_\frac{\alpha}{2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\Bigr)
2つの母比率p1、p2の差(p1-p2)の100(1-α)%信頼区間:
\Bigl(\hat{p_1}-\hat{p_2}-Z_\frac{\alpha}{2}\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} , \hat{p_1}-\hat{p_2}+Z_\frac{\alpha}{2}\sqrt{\frac{\hat{p_1}(1-
\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} \Bigr)
2.3 分散の区間推定
母分散$\sigma^2$の信頼区間は、以下のように求めることができます。
分散σ2乗の100(1-α)%の信頼区間:
\Bigl(\frac{(n-1)u^2}{\chi^2_\frac{\alpha}{2}(n-1)} ,
\frac{(n-1)u^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)}\Bigr)
$t_\frac{\alpha}{2}(n-1)$、$t_\frac{\alpha}{2}(n_1+n_2-2)$、$\chi^2_\frac{\alpha}{2}(n-1)$、$\chi^2_{1-\frac{\alpha}{2}}(n-1)$ の「$(n-1)$」や「$(n_1+n_2-2)$」の部分は自由度を意味しています。t分布や$\chi^2$分布は自由度ごとに異なります。示された自由度の値を読み取るよう注意してください。
3. もっと詳しく(興味がある方向け)
このように標本から母集団を推測する際、確率分布(モデル)を使って母集団を推測しています。平均、母比率、分散のそれぞれについて、最も基本的なパターンを通してもう少し深堀していきます。
3.1 母平均・母比率の推定のために(中心極限定理)
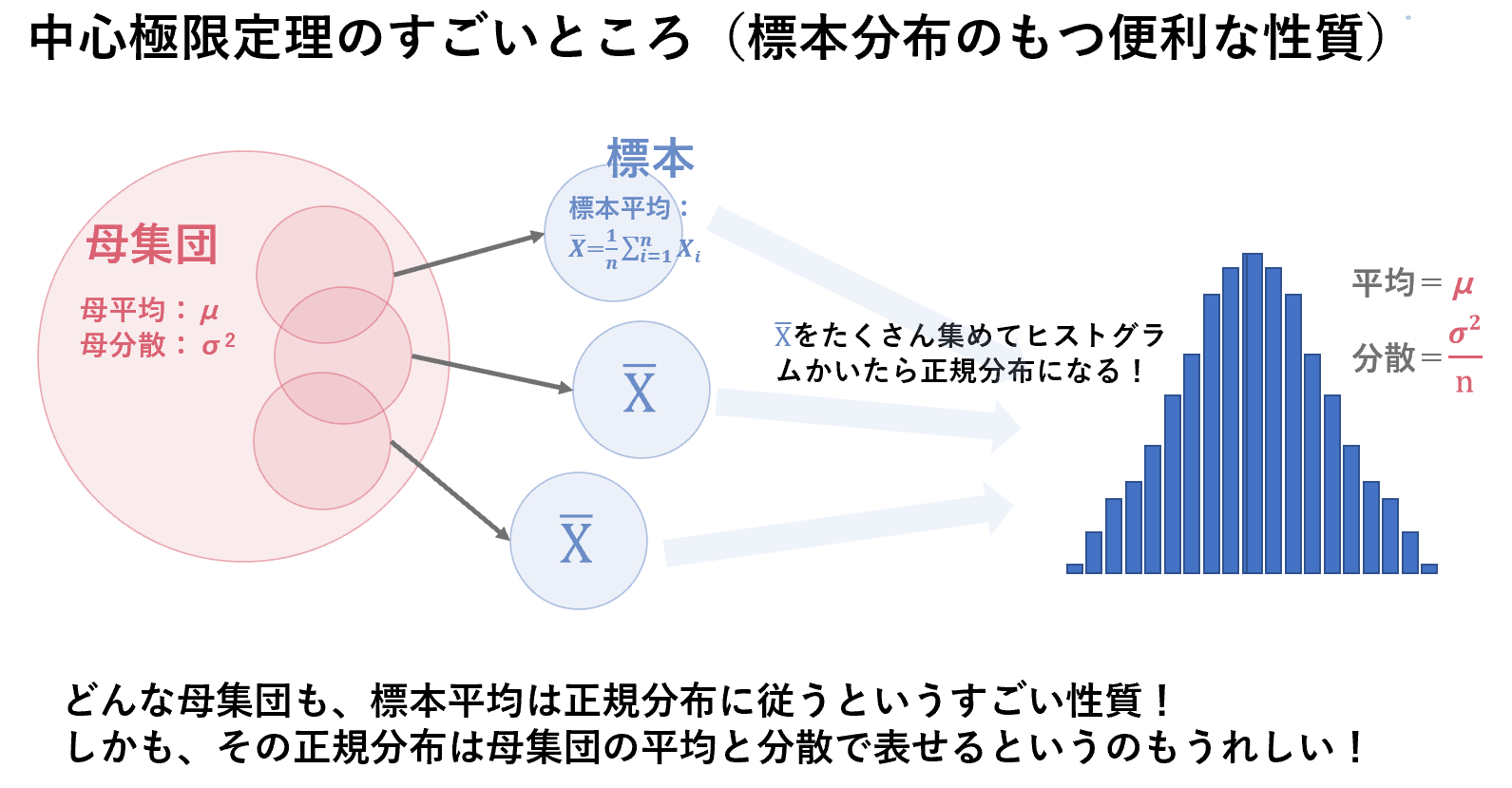
平均や母比率の推定を行うにあたって、中心極限定理という重要な定理があります。これは、母集団がどんな分布であっても、サンプルサイズ$n$が大きいときに、平均が$\mu$(母平均そのもの)、分散が$\frac{\sigma^2}{n}$(母分散をサンプルサイズで割ったもの)の正規分布で近似できるというものです(この詳細が気になる方は、モーメント母関数やテイラー展開を使った説明がありましたので「統計検定1級対応 統計学」を確認してみてください)。また、サンプルサイズ$n$が小さいときは、正規分布ではなく、t分布という便利な分布で近似できるため、$n$が小さくても心配いりません。
この標本平均が正規分布(または、t分布)で近似できるという便利な性質を使って、標本から母集団を推定していきます。
[補足:標本平均の平均・分散について]
$E(\bar{X})=E(\frac{1}{n}\sum{X_i})=\frac{1}{n}\sum{E(X_i)}=\frac{1}{n}n\mu=\mu $
$V(\bar{X})=V(\frac{1}{n}\sum{X_i})=\frac{1}{n^2}\sum{V(X_i)}=\frac{1}{n^2}n\sigma^2=\frac{\sigma^2}{n}$
3.1 平均の推定
まずは、最も基本的な母平均の区間推定からはじめたいと思います。母平均は、標本平均と標準正規分布を使って推定できます。前項記載の通り、標本平均は正規分布で近似できます。この正規分布を標準化し、標準正規分布とすることでさらに扱いやすくして、母平均を推定します。
標準化とは、平均を0、分散を1にすることです。具体的には$\mu$ずらし(減算)、$\frac{\sigma^2}{n}$で圧縮(割り算)します。標準化変量$Z = \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$によって標本平均の分布を標準正規分布で扱うことができるようになります。
3.2 母比率の推定
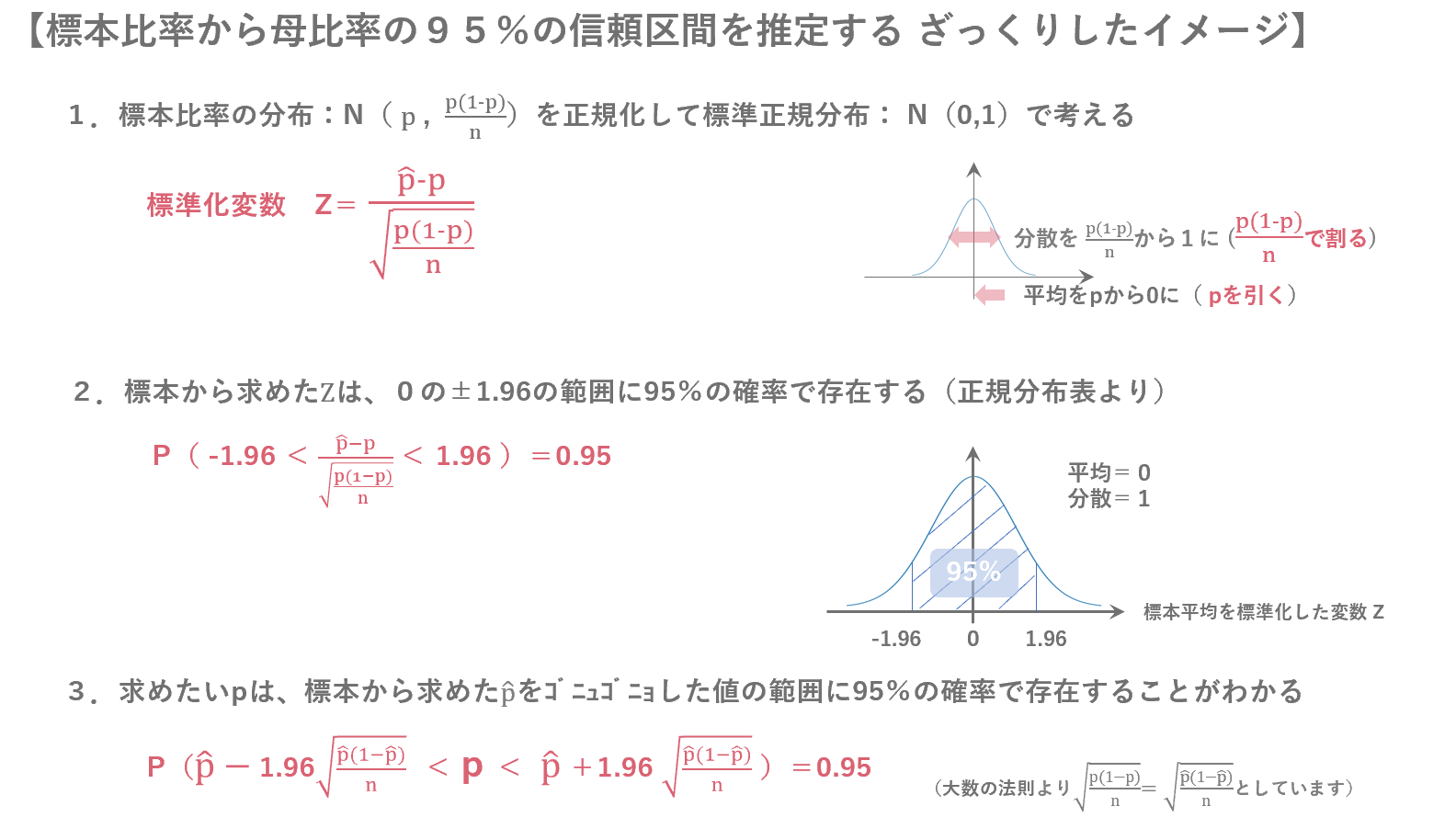
母比率の推定は、母集団においてある事象〇〇が起こる確率$p$を推定するものです。母集団の中で〇〇が起こる割合を母比率$p$、標本の中で〇〇が起こる割合を標本比率$\hat{p}$といい、標本比率$\hat{p}$から母比率$p$を推定することを考えるというものです。ここで、起こる、起こらないというそれぞれの要素をそれぞれ$1$、$0$で表現します。すると、各$X_i$は、確率$p$で$1$となり、確率$(1-p)$で$0$となるようなベルヌーイ分布と考えることができます。ベルヌーイ分布は、平均=$p$、分散=$p(1-p)$となる確率分布です。
また、標本平均$\bar{X}$について考えた場合、標本平均$\bar{X}$は標本比率$\hat{p}$の値そのものになっていることがわかります($\bar{X}=\frac{X_1+X_2+...+X_n}{n}$=$\hat{p}$)。
したがって、標本サイズ$n$が十分大きいとき、中心極限定理より標本平均である標本比率は平均=$p$、分散=$\frac{p(1-p)}{n}$の正規分布で近似できることがわかります。さらに、平均の推定の際と同様、標準化変量$z = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}$で標準化を行うことで、標準正規分布を使って母比率を推定することができるようになります。
選挙の当確判定や、テレビの視聴率予測などに利用されています。また、アンケートなどで何人から聞き取りすべきかなど、標本サイズを決定する場合にも役に立ちます。
3.3 分散
母分散の推定において大切な定理として不偏分散$\hat{\sigma^2}$が$\chi^2$分布に従うという定理があります。具体的には、$\frac{(n-1)\hat{\sigma^2}}{\sigma^2}$が$\chi^2(n-1)$分布に従います。この値が$\chi^2$分布に従うという性質を利用して、平均や母比率と同様の流れで分散の区間推定を行っていきます。($\chi^2$分布自体の説明については省略しますので気になる方はこちらの記事で説明していますので参考にしてください。)
母分散の推定では、標本から標本平均$\bar{x}$、不偏分散$\hat{\sigma^2}$を使って母分散を推定していきます。母平均が未知の場合、自由度はn-1になる点を注意しながら、$\chi^2$分布のパーセント点の付表などから下側$\frac{\alpha}{2}$点、上側$\frac{\alpha}{2}$点を読み取り、平均や母比率と同様の計算を行うことで分散の推定をすることができます。
商品の製造工程での偏りなどを検知することなどに役に立ちます。
まとめ
今回は、基本的な平均、母比率、分散の最も基本的な説明だけをしました。他のものも気になる方はぜひ具体的に考えてみてください。
【参考文献、サイト】
本書は筆者たちが勉強した際のメモを、後に学習する方の一助となるようにまとめたものです。誤りや不足、加筆修正すべきところがありましたらぜひご指摘ください。継続してブラッシュアップしていきます。また、様々なモデルの解説書を掲載していますので、興味のある方は、以下のサイトもご参照ください。