統計検定２級の取得向けに整理したチートシートです。

参考としたのは下記の統計検定２級対策の公式本と入門統計学です。

主に確率、統計的推定、統計的仮説検定、線形回帰を中心に記載しています。また、統計検定２級の受験時の（多少参考になるレベルですが）ヒントを記載しています。

本記事はチートシートですので詳細については上記書籍、専門書やネットの記事等をご参照ください。

実際に受験する際は公式の過去問題集（筆記試験向け）での学習が有効です。

確率の問題を多数解きたい人は下記の本もおすすめです。

Webで上記「統計学演習」のPDF版が公開されていますのでこちらも利用すると良いかと思います。

※筆者が所属するNPO法人の勉強用にメモしたものです。専門領域でないため誤りや誤解があるかと思いますので、加筆修正すべきことろがありましたらご指摘ください。継続してブラッシュアップしていきます。

©NPO法人AI開発推進協会

１確率分布

確率分布はとびとびの値をとる「離散型確率分布」と、連続値をとる「連続型確率分布」とがある。

１.１離散型確率分布

２項分布（Binomial Distribution）

成功確率が p(0 ≦ p ≦ 1) である試行を n 回行ったとき、成功の回数が x 、失敗の回数が n - x である確率。　パラメータ(n, p)が与えられると確率分布が決まるので、B(n , p) で表す。また、n＝１ のときは「ベルヌーイ分布（Bernoulli trial）」といい、B(1, p) で表す。

f(x) \hspace{5mm}=\hspace{5mm} {}_nC_x\hspace{1mm} p^x\hspace{1mm}(1 - p)^{n-x}

２項分布での期待値、分散は以下となる。

  期待値　\hspace{5mm} E[X] \hspace{5mm}=\hspace{5mm} np

  分散 　　\hspace{5mm} V[X] \hspace{5mm}=\hspace{5mm} np(1-p)

【テストでのヒント】
・組み合わせ問題では、１つ取ったら元に戻して１づつ取り出す場合に2項分布を使う（複数同時に取り出す時は使わず通常の組み合わせで解く）。
・２項分布を正規分布で近似して確率の問題が解ける。
ただし、 np > 5、n > 50 が条件となる。試行回数が大きなものが出てきた時は、（持ち込み可能な電卓では計算できないので）このパターン（２項分布）で解くことを考える。

ポアソン分布（Poisson Distribution）

２項分布において期待値 np = λ を固定して、試行回数 n -> ∞、成功確率 p -> 0のような極限を取ったときの確率分布となる。成功確率 p が小さいので、「滅多に起こらないものが起こる確率」とも言われる。

f(x) = e^{-\lambda}\hspace{1mm} \lambda^x \hspace{1mm}/ \hspace{1mm} x!

ポアソン分布での期待値、分散は以下となる。

  期待値　E[X]\hspace{5mm}=\hspace{5mm} \lambda

  分散 　　V[X]\hspace{5mm}=\hspace{5mm} \lambda

【テストでのヒント】
テストでは関数電卓は使えないので、あらかじめ指数計算値が出されている。
e^λ が与えられているとき、e^-λ は下記で計算する。

  e^{-λ} \hspace{5mm}=\hspace{5mm} \frac{1}{e^\lambda}  \hspace{30mm}

したがって、e² = 7.39 が与えられたとき, e^-2 = 1 / 7.39 = 0.135　となる。

幾何分布（Geometric Distribution)

成功の確率が p であるベルヌーイ試行を最初に正解するまで繰り返したときの試行回数 X の確率分布。　最初に成功するのが x 回目であるので、x - 1 回目までは失敗なので確率分布は以下となる。

f(x) \hspace{5mm}=\hspace{5mm} p\hspace{1mm}(1 - p)^{x-1}

幾何分布での期待値、分散は以下となる。

  期待値　E[X] \hspace{5mm}=\hspace{5mm} \frac{1}{p}

  分散 　 V[X] \hspace{5mm}=\hspace{5mm} \frac{1 - p}{p^2}

１.２　連続型確率分布

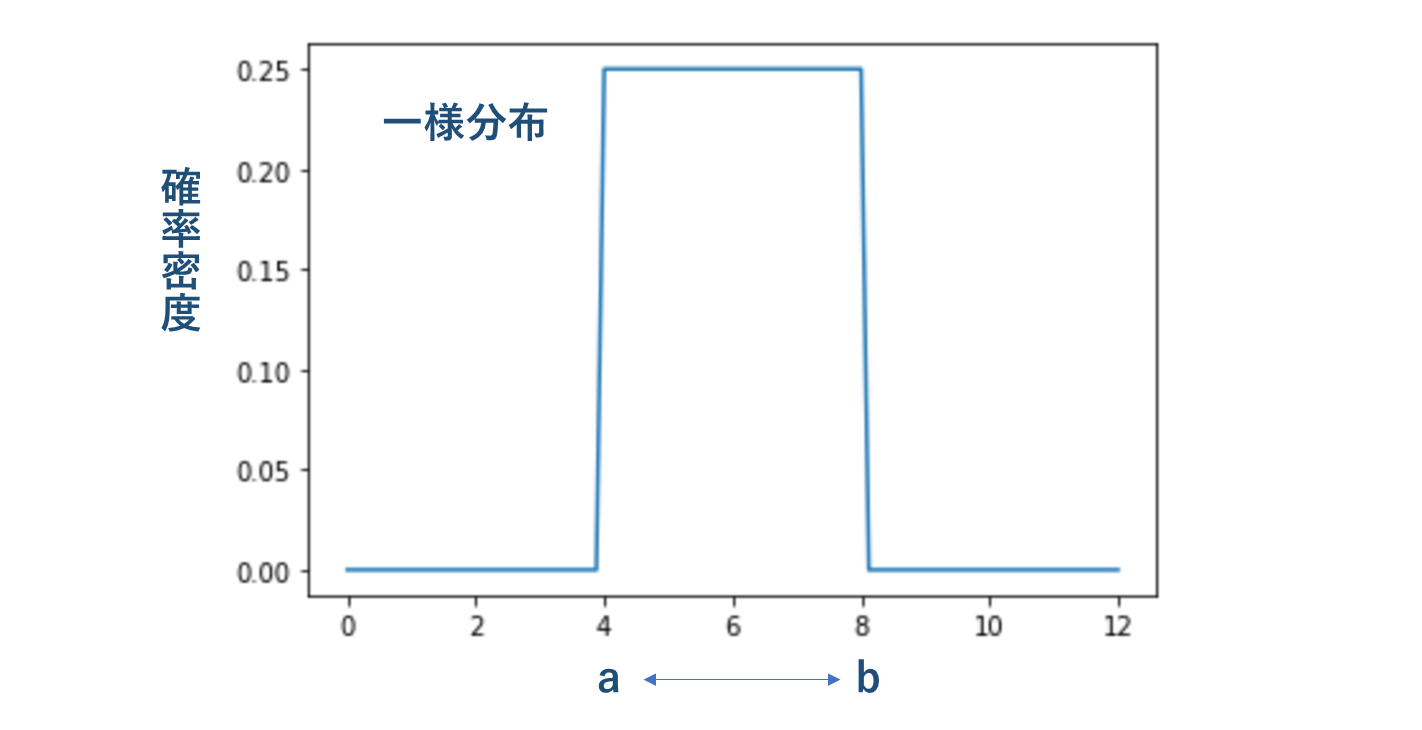
一様分布（Uniform Distribution）

区間 [a, b] 内のどの値も同じ起こりやさをもつ分布を一様分布と呼び、U(a, b) で表す。

代表的なものは乱数生成である。
一様分布の確率密度関数は以下で表す。

f(x) = \left\{
\begin{array}{ll}
\frac{1}{b - a} & (a \leq x \leq b) \\
0 & (そのほか)
\end{array}
\right.

一様分布での期待値、分散は以下となる。

  期待値 \hspace{5mm} E[X]\hspace{5mm}=\hspace{5mm} \frac{a + b}{2}

  分散  \hspace{5mm}　V[X]\hspace{5mm}=\hspace{5mm} \frac{(b - a)^2}{12}

正規分布（Normal Distribution）

連続型確率分布の中の代表的な確率分布で、確率密度関数は以下で表す。

  f(x) \hspace{5mm}=\hspace{5mm} \frac{1}{\sqrt{2\pi\sigma^2}} \hspace{1mm} exp \hspace{1mm} \Biggl( - \frac{(x - \mu)^2}{2\sigma^2}  \Biggr)

μ は期待値（平均）、σ² は分散を示し、μ と σ² によって決まるので記号 N (μ, σ² )で表す。
確率変数 X が正規分布 N(μ,σ²) に従うとき、確率変数を、

  Z \hspace{5mm}=\hspace{5mm} ( X - \mu )\hspace{1mm} / \hspace{1mm} \sigma

のように変換すると、Z は平均 0、分散 1 の標準正規分布（Standard Normal Distribution、記号 N(0, 1) で表す）に従う。
このときの確率密度関数は以下となる。

  f(x) \hspace{5mm}=\hspace{5mm} \frac{1}{\sqrt{2\pi}} \hspace{1mm} exp \hspace{1mm} \Biggl( - \frac{x^2}{2}  \Biggr)

【テストでのヒント】
・標準化された Z 変数を求めることで確率を求めることができる。すなわち平均（＝期待値）と分散が分かれば確率を求めることができる。
・テストでは標準正規分布の上限確率の一覧表が提示される。
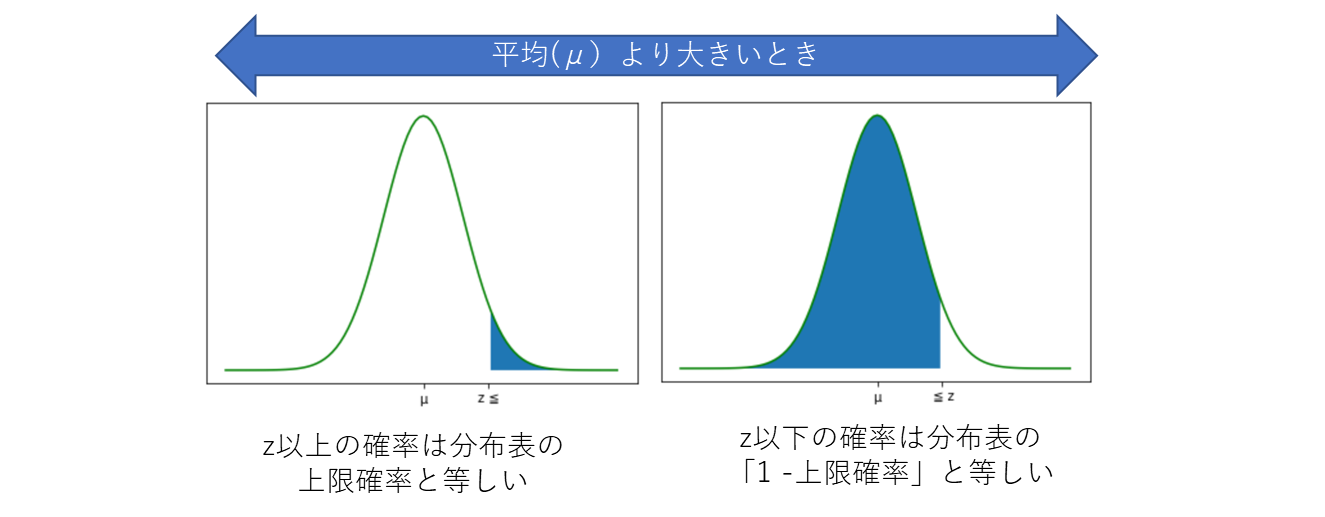
・z が平均より高い場合、z以上 となる確率を求める場合は「一覧表の上限確率値」が確率となる。　z以下 となる確率を求める場合は、「1 - 一覧表の上限確率値」となる。

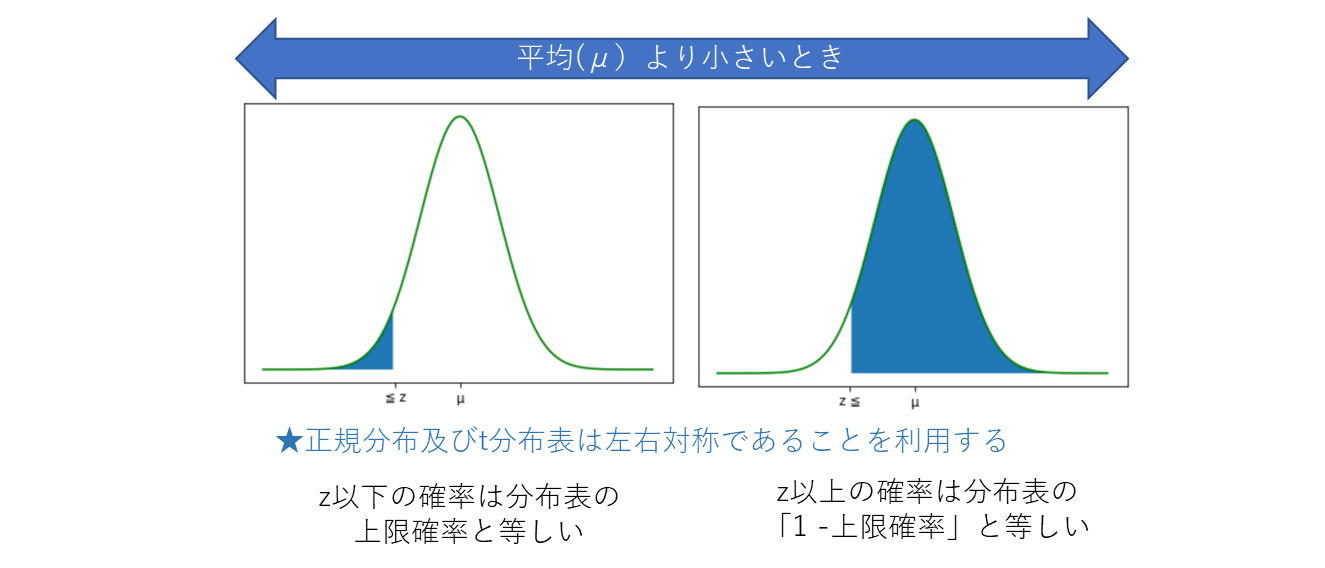
・z が平均より低い場合、 z以上 となる確率を求める場合は「1 - 一覧表の上限確率値」が確率となる。　z以下 となる確率を求める場合は、「一覧表の上限確率値」が確率となる。

・離散型の確率分布でも標準正規分布を使って近似的に確立を求めることができる。
例えば、２項分布で試行回数 n と確率 p がわかっている場合、

   μ \hspace{5mm}=\hspace{5mm} E[X] \hspace{5mm}=\hspace{5mm} np

   σ^2 \hspace{2mm}=\hspace{2mm} V[X] \hspace{2mm}=\hspace{2mm} np(1 - p) , \hspace{10mm} σ \hspace{2mm}=\hspace{2mm} \sqrt{np(1 - p)}

となり、Z = (x - μ) / σ を求め、あとは標準確率分布の上限表から確率を求める。
これを２項分布の正規近似という。
n が十分に大きく、np > 5 かつ np(1 - P)　> 50 を満たすとき近似は十分とされる。
逆にテストでは n が大きければ電卓では計算が不可能なため、ほぼ２項分布の正規近似で解くことになる。

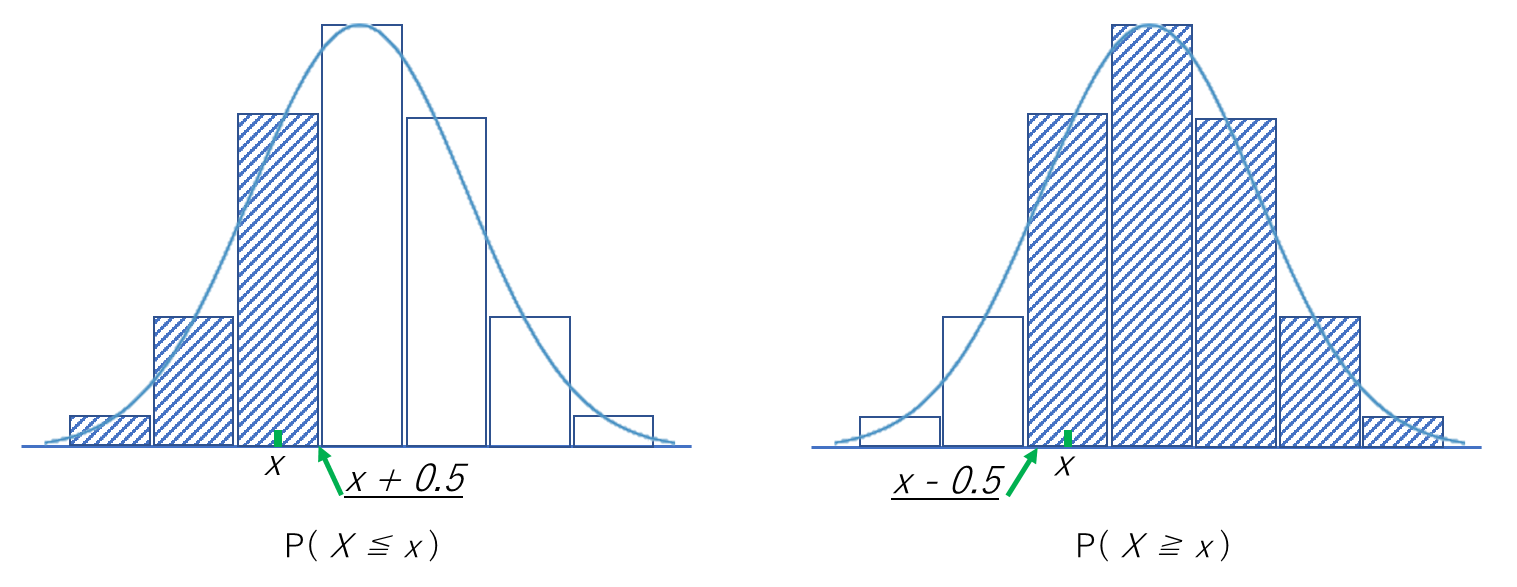
※なお、半整数補正を行うことでより正確な値を求めることもできる。
　・P(X ≦ x )、すなわちx以下の確率を求める場合、「x + 0.5」とする
　・P(X ≧ x )、すなわちx以上の確率を求める場合、「x - 0.5」とする

指数分布（Exponential Distribution）

ポアソン分布は「滅多に起こらないものが起こる確率（回数）」であったが、同じランダムな現象に対して初めて起こるまでの「期間（時間）」の確率分布が指数分布である。
指数分布の確率密度関数は以下となる。

   f(t) \hspace{5mm}=\hspace{5mm} \lambda e^{-\lambda t}

幾何分布での期待値、分散は以下となる。

  期待値　\hspace{5mm} E[X]\hspace{5mm}=\hspace{5mm} \frac{1}{\lambda}

  分散   \hspace{5mm} V[X]\hspace{5mm}=\hspace{5mm} \frac{1}{\lambda^2}

１.３　歪度と尖度

歪度（わいど）
　非対称の大きさを表す。　正規分布や t 分布のような左右対称の分布では歪度はゼロとなり、右に裾が長い分布では正の値、左に裾が長い分布では負の値となる。

標本歪度 \hspace{5mm}=\hspace{5mm} \frac{1}{n} \sum_{i=1}^n \frac{(x_i - \bar{x})^3}{s^3}

* s は標本標準偏差

尖度（せんど）
分布の尖り具合と裾の広がり具合を表す。正規分布に従うときは尖度 = 0 となり、正規分布と比較して尖っていて裾の長い分布（t分布）の尖度は正の値になり自由度が大きいほど尖度はゼロに近づき正規分布に近づく。一方、正規分布より裾の短い分布である一様分布の尖度は負の値となる。

標本尖度 \hspace{5mm}=\hspace{5mm} \frac{1}{n} \sum_{i=1}^n \frac{(x_i - \bar{x})^4}{s^4} \hspace{5mm} - 3 \hspace{5mm}

*s は標本標準偏差
*正規分布での４次モーメントは３であり、上記式での「−３」は正規分布での標本尖度がゼロとなるように調整したもの

正規分布の４次モーメント \hspace{3mm} \frac{1}{n} \sum_{i=1}^n \frac{(x_i - \bar{x})^4}{s^4} \hspace{5mm}=3

１.４　確率分布のまとめ

主な確率分布の確率密度関数、期待値、分散をまとめると下記の表になる。

確率分布	タイプ	確率密度関数	期待値	分散
２項分布	離散	_nC_x p^x (1 - p)^{n - x}	np	np (1 - p)
ポアソン分布	離散	e^-λλ^x / x!	λ	λ
幾何分布	離散	p (1 - p)^{x - 1}	1 / p	(1 - p) / p²
正規分布	連続	1/√2πσ² exp {- (x - μ）² / (2σ²) }	μ	σ²
標準正規分布	連続	1/√2π exp {- x² / 2 }	0	1
指数分布	連続	λe^-λt	1/λ	1/λ²

２　確率のおさらい（補足）

ここで、確率のおさらいです。　すでに理解している人は読み飛ばしてください。

２．１　各種公式

加法定理 P(A ∪ B)

P(A ∪ B) \hspace{5mm}=\hspace{5mm} P(A)  +  P(B)  - P(A ∩ B)

条件付き確率 P(B | A)

P(B|A) \hspace{5mm}=\hspace{5mm} \frac{P(A ∩ B)}{P(A)}

乗法定理 P(A ∩ B)

P(A \cap B) \hspace{5mm}=\hspace{5mm} P(A)P(B|A)

ベイズの定理

P(H_i|A) \hspace{5mm}=\hspace{5mm} \frac{P(H_i)P(A|H_i)}{P(A)}

分母のP(A)は複数の原因によっておこる事象Aの総合的な生起確率を表す。

∴  P(H_i|A) \hspace{5mm}=\hspace{5mm} \frac{P(H_i)P(A|H_i)}{\sum_{j=1}^{n} P(H_j)P(A|H_j)}

確率変数と独立と排反

事象 A と Bが独立であるとき、

P(A \cap B) \hspace{5mm}=\hspace{5mm} P(A)\hspace{1mm}P(B)

が成り立つ。

事象 A と Bが排反であるとき、

P(A \cap B) \hspace{5mm}=\hspace{5mm} P(\emptyset) \hspace{5mm} = \hspace{5mm} 0

が成り立つ。

２.２　期待値と分散

期待値

[離散型]

E[X] \hspace{5mm}≡\hspace{5mm} \sum_{i} x_id(x_i) = \mu  \\
E[u(x)] \hspace{5mm}=\hspace{5mm} \sum_{t} u(x_i)\hspace{2mm}f(x_t)

[連続型]

E[X] \hspace{5mm}≡\hspace{5mm} \int_{-\infty}^{\infty} x\hspace{2mm}f(x)\hspace{1mm}dx = \mu \\
E[u(x)] \hspace{5mm}=\hspace{5mm} \int_{-\infty}^{\infty} u(x)\hspace{2mm}f(x)dx

分散

[離散型]

V[X] \hspace{2mm}≡\hspace{2mm} E[ (X - \mu)^2] \hspace{2mm}=\hspace{2mm} \sum_{i} (x_i - \mu)^2 \hspace{1mm} f(x_i) \hspace{2mm}=\hspace{2mm} \sigma^2

[連続型]

V[X] \hspace{2mm}≡\hspace{2mm} E[ (X - \mu)^2] \hspace{2mm}=\hspace{2mm} \int_{-\infty}^{\infty} (x - \mu)^2 \hspace{1mm} f(x)\hspace{1mm}dx \hspace{2mm}=\hspace{2mm} \sigma^2

共分散、相関係数

[共分散]

s_{xy} \hspace{5mm}=\hspace{5mm} \frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})

[相関係数]

r_{xy} \hspace{5mm}=\hspace{5mm} \frac{s_{xy}}{s_x\,s_y}  \\
*s_x,s_y は x, yの標準偏差

２．３　確率変数の公式

E[X + Y] \hspace{5mm}=\hspace{5mm} E[X] + E[Y]

E[aX] \hspace{5mm}=\hspace{5mm} aE[X]

E[X + c] \hspace{5mm}=\hspace{5mm} E[X] + c

V[X] \hspace{5mm}=\hspace{5mm} E[X^2] - \left\{E(X)\right\}^2

  \hspace{50mm} \ast ここでV[X]= \sigma^2、E(X)=\mu であるので、 E[X^2] = \sigma^2 + \mu^2

V[aX] \hspace{5mm}=\hspace{5mm}a^2\hspace{1mm}V[X]

V[X + c] \hspace{5mm}=\hspace{5mm}V[X]

V[X + Y] \hspace{5mm}=\hspace{5mm} V[X] + V[Y] + 2Cov[X, Y]

V[X - Y] \hspace{5mm}=\hspace{5mm} V[X] + V[Y] - 2Cov[X, Y]

Cov[X, Y] \hspace{5mm}=\hspace{5mm} E[X\,Y] - E[X]\,E[Y]

Cov[X, X] \hspace{5mm}=\hspace{5mm} V[X]

Cov[aX + b, cY + d] \hspace{5mm}=\hspace{5mm} acCov[X, Y]

Cov[X + Y, Z] \hspace{5mm}=\hspace{5mm} Cov[X, Z] + Cov[Y, Z]

【テストでのヒント】

確率の問題は「統計学演習」やネット記事等でさまざまな問題を事前に解いておいた方が良い。
連続型の確率密度関数を使った期待値、分散の計算について、下記の算出式をベースに過去問題から様々なパターンに対応できるようにする。

①期待値を求める　  \hspace{2mm}　　E[X] \hspace{2mm}=\hspace{2mm} \int_{a}^{b} x\hspace{2mm}f(x)\hspace{1mm}dx  \hspace{50mm}\\

②分散を求める \hspace{2mm}　
V[X] \hspace{1mm}=\hspace{1mm} E[x^2] - \left\{E(x)\right\}^2  \hspace{1mm}
=\hspace{1mm}\int_{a}^{b} x^2 \hspace{1mm}f(x)\hspace{1mm}dx -\hspace{1mm}①^2

【相関係数の使用の例】
相関係数を使用した計算の例としてはTOEICのスコアがある。
例えば、
Listening（L)：平均値=Lμ   標準偏差=Ls
Reading（R)：平均値=Rμ  標準偏差=Rs
Total（T)：     平均値=Tμ  標準偏差=Ts
の時のListingとReadingの相関係数 r_LR は以下の式で求めることができる。

\hspace{2mm}　　V[L+R] \hspace{2mm}=\hspace{2mm} V[L]\hspace{2mm}+\hspace{2mm}V[R]\hspace{2mm}+\hspace{2mm}2Cov[L,R] \\

\hspace{2mm}2Cov[L,R]\hspace{2mm}=\hspace{2mm}　V[L+R]\hspace{2mm}- V[L]\hspace{2mm}-V[R]

\begin{align}
\hspace{2mm}Cov[L,R]\hspace{2mm}&=\left\{V[L+R]\hspace{2mm}- V[L]\hspace{2mm}-V[R]\right\}\hspace{2mm}/\hspace{2mm} 2 \\
&= \big(Ts^{2} - Ls^{2} - Rs^{2}\big)\hspace{2mm}/\hspace{2mm} 2 
\end{align} \\

\begin{align}
\therefore \hspace{2mm}r_{LR} &= Cov[L,R] \hspace{2mm} / \hspace{2mm} \big(Ls・Rs\big) \\
&= \left\{\big(Ts^{2} - Ls^{2} - Rs^{2}\big) \hspace{2mm} / \hspace{2mm} 2 \hspace{2mm}\right\} \hspace{2mm} / \hspace{2mm} \big(Ls・Rs \big) \quad
\end{align}

３　標本分布

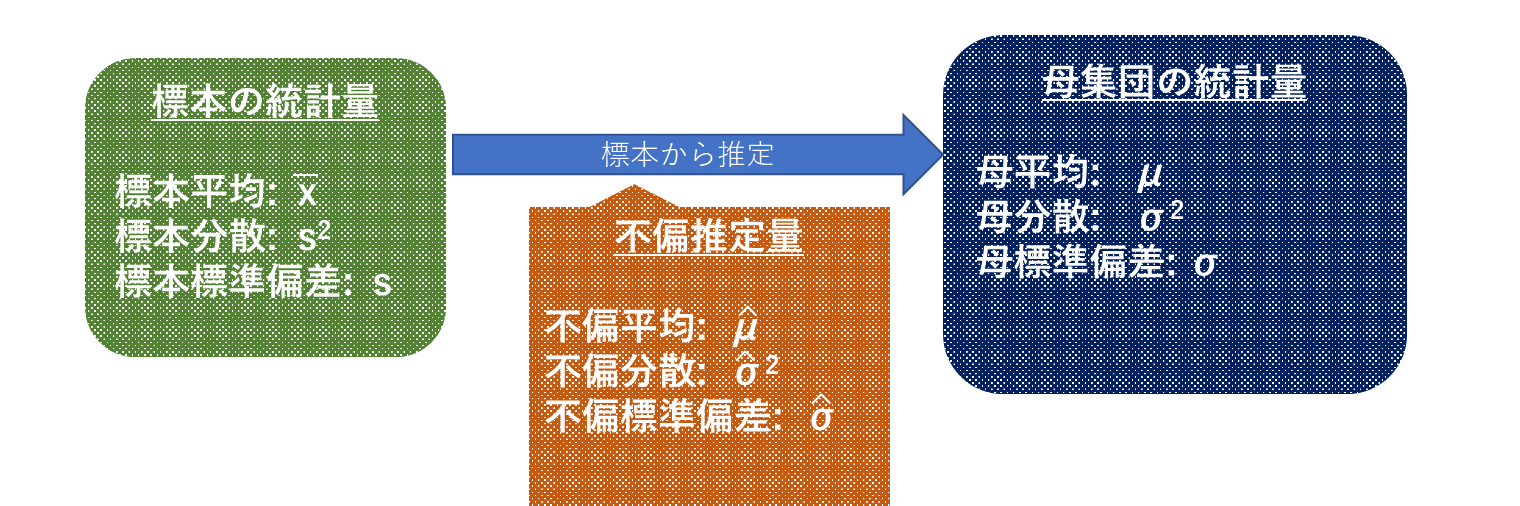
３．１　母集団、標本、不偏推定量

推測しようとする対象全体を母集団、母集団から抽出し調査や実験に使うデータを標本、標本データを使って母集団の統計量を推定した値を不偏推定量と呼ぶ。

標本分布（標本平均の分布）

推測統計では個々の値ではなくいくつかの標本から計測された平均＝標本平均 x^- の分布について検討するものである。この標本平均のx^- の分布を標本分布と呼ぶ。標本分布はサンプル数との間に「サンプル数が大きくなるほど標本分布のバラツキ（誤差）は小さくなる」という重要な関係がある。
標本分布での平均、分散は以下となる。

母集団の平均 = \mu 、分散　= \sigma^2 とする\\
x \:=\: x_1 \:+\: x_2 \:+\: \:・・・\: x_n  \hspace{5mm}   \leftarrow 母集団からn個のサンプルを無作為に抽出 \\
E[\bar{x}] \:=\: \frac{1}{n} \sum_{i=1}^n {E[x_i]}  \:=\:  \frac{1}{n} * (n * \mu) \:=\: \mu \\
V[\bar{x}] \:=\: \biggl(\frac{1}{n}\biggr)^2  \sum_{i=1}^n {V[x_i]}  \:=\: \biggl(\frac{1}{n}\biggr)^2 \sum_{i=1}^n \sigma^2 \:=\: \biggl(\frac{1}{n}\biggr)^2 n\sigma^2 \:=\: \frac{\sigma^2}{n}

標準誤差

標準誤差(standard \hspace{2mm} error)  \hspace{5mm}  se \hspace{5mm} = \hspace{5mm} \frac{\sigma}{\sqrt{n}}

✳︎標準誤差と変動係数(CV, coefficient of variation)に注意
変動係数は標準偏差を平均で標準化（平均で割ることで相対的なばらつきを表す）したものである。

変動係数 \hspace{5mm}  CV \hspace{5mm} = \hspace{5mm} \frac{\sigma}{\mu}

不偏分散

不偏分散  \hspace{5mm}  \hat{\sigma}^2 \hspace{5mm} = \hspace{5mm} \frac{1}{n - 1} \sum_{i=1}^n (x_i - \bar{x})^2

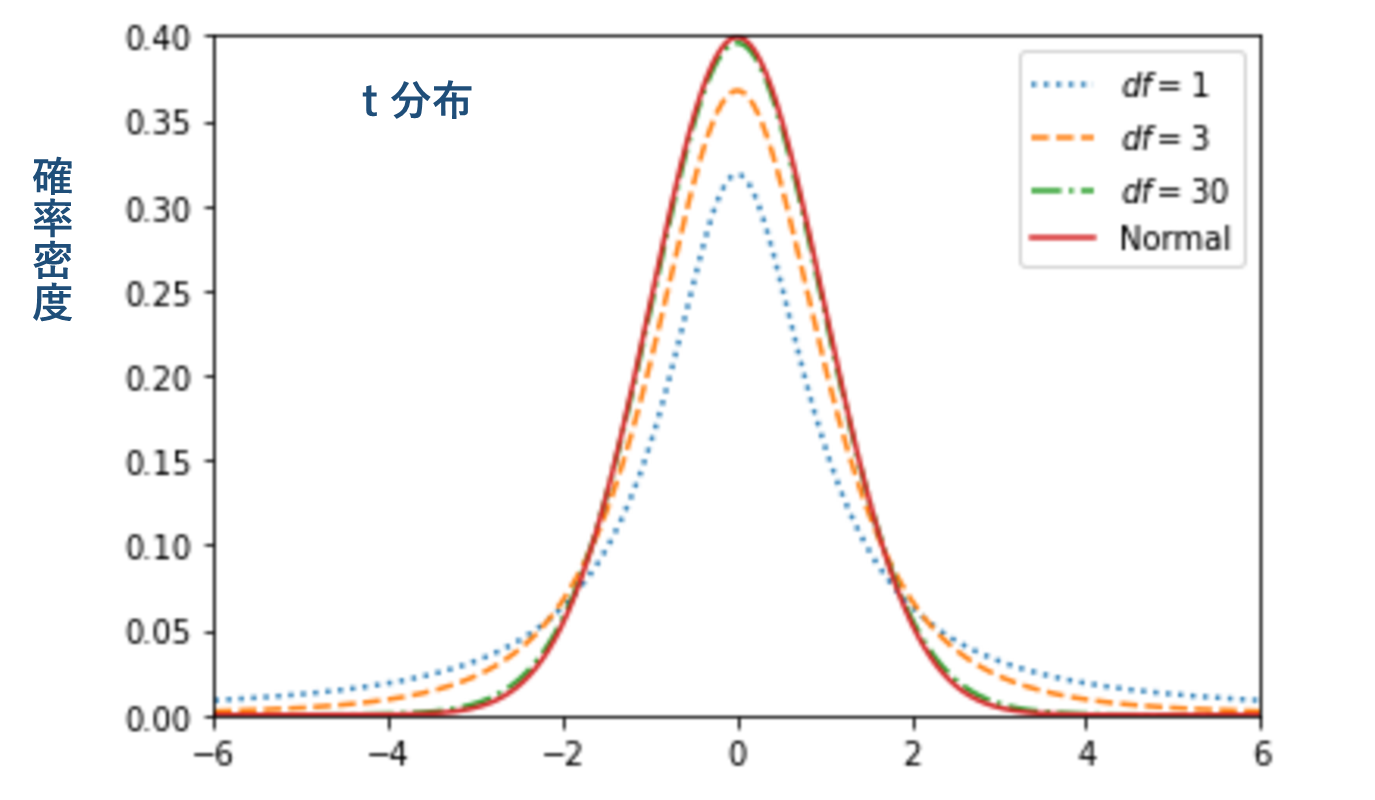
３．２　t 分布

独立な2つの確率変数 Z と W があり、Z が標準正規分布 N（0, 1)、W が自由度 m の χ² 分布に従うとき、下記の式に従う分布を自由度 m の t 分布と呼ぶ。
母分散が未知でサイズの小さな標本から母平均などを推定／検定を行う際に標準正規分布の代わりに用いる。

t \hspace{5mm}=\hspace{5mm} \frac{Z}{\sqrt{W/m}}

自由度 m が大きくなると正規分布に近づく。

また、観測値の場合の t は下記となり、

t \hspace{3mm}=\hspace{3mm} \sqrt{n} (\bar{x} - \mu) \hspace{1mm}/\hspace{1mm} \hat{\sigma}  \hspace{3mm}=\hspace{3mm} \sqrt{n - 1} \hspace{1mm}(\bar{x} - \mu) \hspace{1mm}/\hspace{1mm} s \\

自由度 n - 1 のt分布に従う。

【テストでのヒント】
t値の計算は不偏標準偏差を使う場合はサンプル数 n　（標本標準偏差を使う場合はサンプル数 n - 1　)、t分布の表を参照するときは n - 1の値を参照する。

３．３　χ^２分布

χ²分布は標準化変量 z を２乗和した χ² 値が従う確率分布。　母分散の信頼区間の推定やクロス集計表の検定に用いる。　χ² 分布は、検定のために作り出された分布である。

自由度 df が大きくなると徐々に正規分布に近づく。

z_i \hspace{5mm}=\hspace{5mm} \frac{x_i - \mu}{\sigma} \\
\chi^2 \hspace{5mm}\equiv\hspace{5mm} z^2 \hspace{5mm}=\hspace{5mm} \frac{(x - \mu)^2}{\sigma^2}

χ²値 は以下になる。

\chi_{(n)}^2 \hspace{5mm}\equiv\hspace{5mm} \sum_{i=1}^n z_i^2 \hspace{5mm}=\hspace{5mm} \frac{\sum_{i=1}^n (x_i - \mu)^2}{\sigma^2} \\
 
\chi_{(n)}^2 \hspace{5mm}=\hspace{5mm} \frac{(n\,-\,1)s^2}{\sigma^2} \\

自由度(df=n)の χ² 分布の期待値と分散は下記となる。

期待値
E[X] = n
分散
V[X] = 2n

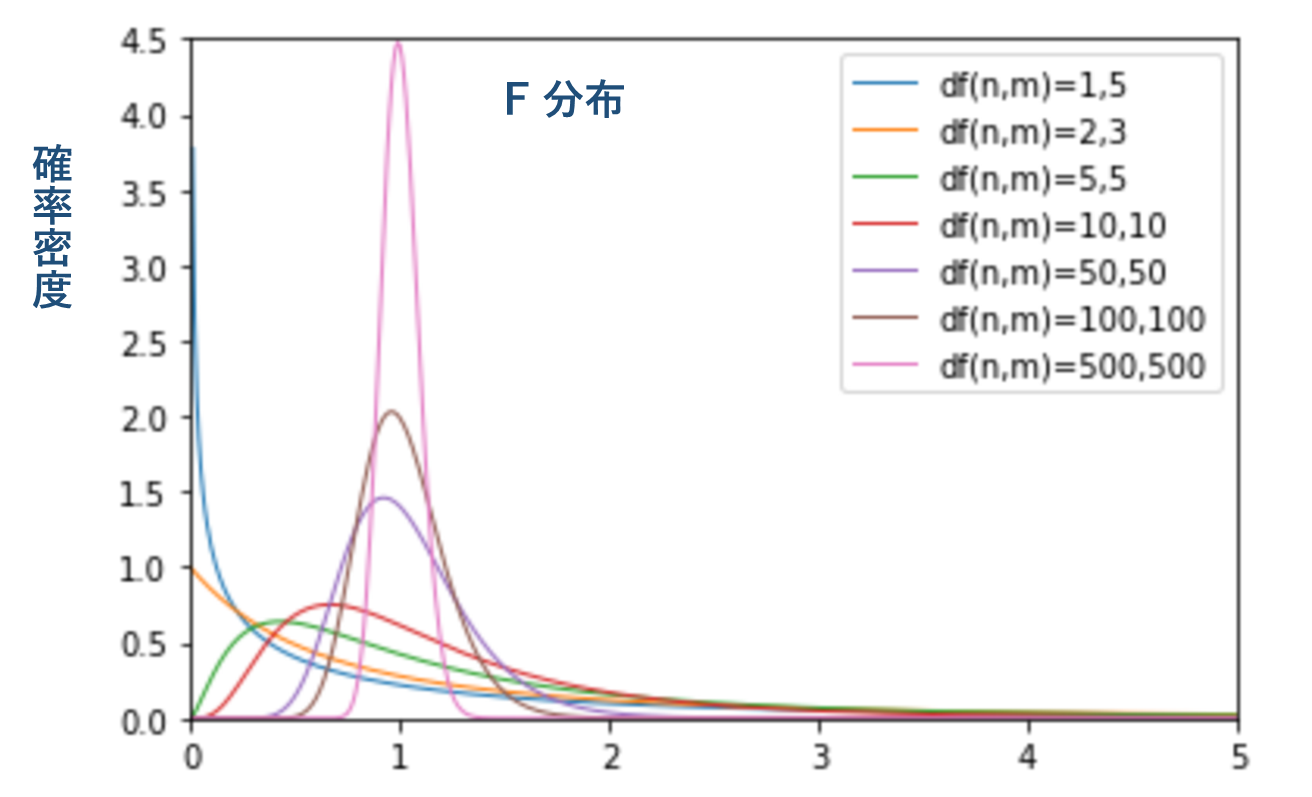
３．４　F分布

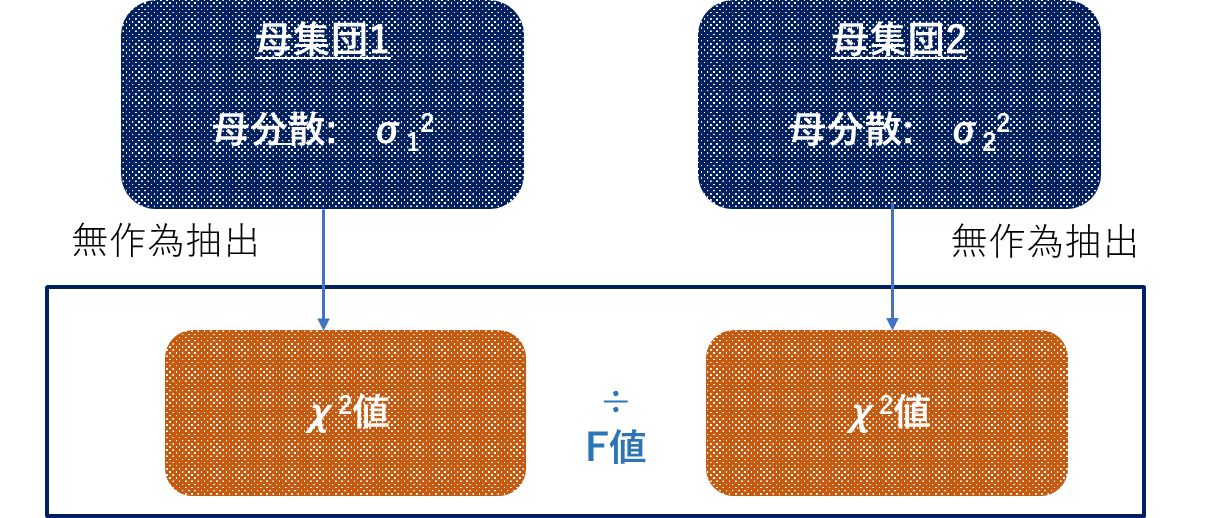
F分布は独立した２つの χ² 値の比であるF値が従う確率分布。等分散性の検討や分散分析に用いる。
2つの確率変数 W₁、W₂があるとき、それぞれの自由度で割った比を取った、

F \hspace{5mm}=\hspace{5mm}  \frac{W_1 / \nu_1}{W_2 / \nu_2}

に従う分布を自由度 (ν₁, ν₂) のF分布という。

2つの自由度によって分布の形は変化し、両方の自由度が大きい場合は平均はほぼ１となる。

（他の確率分布が正規分布に従った母集団から無作為に抽出した標本に基づいた統計量が従う分布であるのに対し）F分布は「２つの母集団」から無作為に抽出した「２つの標本」に基づいた統計量が従う分布であり、標準正規分布に従う２つの母集団から無作為抽出した２つの χ の２乗値の比であるF値の確率分布となる。

F値は、2つの χ² の自由度をそれぞれ ν₁、　ν₂とすると以下の式で表す。

F_{(\nu_1,\hspace{1mm}\nu_2)} \hspace{5mm}=\hspace{5mm} \frac{\frac{\chi_{(\nu_1)}^2}{\nu_1}}{\frac{\chi_{(\nu_2)}^2} {\nu_2}}

また、不偏分散を使った場合は下記の式で表す。

F_{(\nu_1,\hspace{1mm}\nu_2)} \hspace{5mm}=\hspace{5mm} \frac{\frac{\nu_1 \hat{\sigma_1^2}}{\sigma_1^2} / \nu_1}{\frac{\nu_2 \hat{\sigma_2^2}}{\sigma_2^2} / \nu_2} \\ 
\,  =\hspace{5mm} \frac{\hat{\sigma_1^2}}{\sigma_1^2}・\frac{\sigma_2^2}{\hat{\sigma_2^2}}

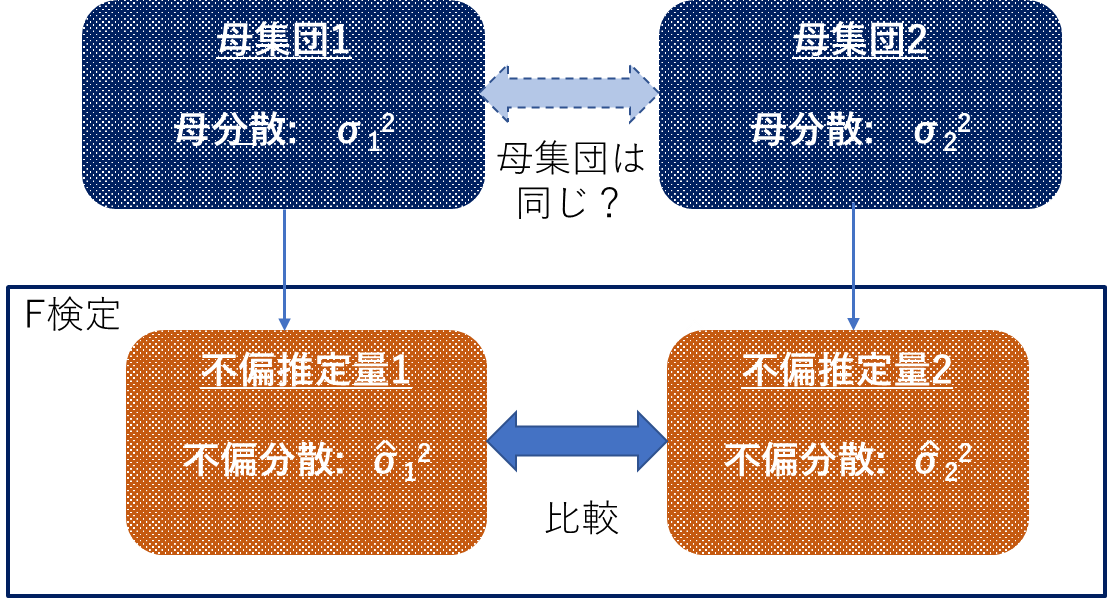
ここで、母分散が等しいとした場合、

\frac{\sigma_2^2}{\sigma_1^2} \hspace{5mm}=\hspace{5mm} 1

となるため、

F \hspace{5mm}=\hspace{5mm} \frac{\hat{\sigma_1^2}}{\hat{\sigma_2^2}}

このF値を統計検定量として、抽出元である２つの母集団の分散が同じかを検定する等に用いられる。

３．５　その他

大数の法則（law of large numbers）

多数回の試行の結果として得られたデータの平均や相対度数が、確率分布の平均や生起確率に近づくこと。

中心極限定理（central limit theorem）

n 個の確率変数 X_nの標本平均の分布は、　n が大きくなるにつれて（もとの分布が正規分布でない場合でも）正規分布に近づくこと。

フィッシャーの３原則（Fisher's three principle）

①無作為化（randomization）
②繰り返し（replication）
③局所管理（local control）

標本抽出方法

単純無作為抽出法
最も基本的な方法であり、母集団から乱数表を用いて必要数だけサンプルを抽出する。　母集団から完全に無作為に調査対象を取り出す必要があり一般的に手間と時間がかかる。
系統抽出法
母集団のデータ全てに番号をつけて、１番目のデータを無作為に抽出し、２番目以降は同じ間隔でデータを抽出する方法。
層化無作為抽出法
母集団をいくつかの層に分けて、各層からまんべんなくランダムにデータを抽出する方法。
多段抽出法、層化多段抽出法
抽出単位を何段階かに分けて逐次的に抽出していく方法。段数が多くなるほど平均などの推定精度は悪くなる。この欠点を補うために層化抽出法を組み合わせたものが層化多段抽出法。
クラスター（集落）抽出法　母集団を網羅的に分割し小集団（クラスター）を構成した後、いくつかのクラスターのそのクラスター内の全てのデータを抽出する。

【テストでのヒント】

ν₁ = 1、 ν₂ = m の場合、t分布の２乗値が F(1, m) に等しくなる。 t値が与えられたときのF値を求められる場合(＆分子の自由度が１のとき）は、t² = Fを用いて算出する。
標本抽出方法については、各抽出方法を過去問題をベースにユースケースを踏まえて理解しておく。

４　統計的推定と仮説検定

標本から真（母数）の平均や分散の範囲を確率的に推定したり（統計的推定）、複数の標本群の背景にある母集団が同じか否か（平均や分散などに差があるかどうか）を確率的に判定する（仮説検定）。

基本的な計算プロセスはほぼ同様だが、仮説検定では「帰無仮説 H₀ （本来の目的とは逆となる従来とは差がないこと）を立てて、仮説の下で起こりやすさを算出し、滅多に起きないことが確率的に起きたと考えられる場合に、帰無仮説が間違えであった」と判断し、対立仮説 H₁ (帰無仮説を否定して差がないとは言えない）
を採択する。また、この「滅多に起きない確率で帰無仮説を棄却する領域」を有意水準 α と呼ぶ。

４.１　仮設検定の構造

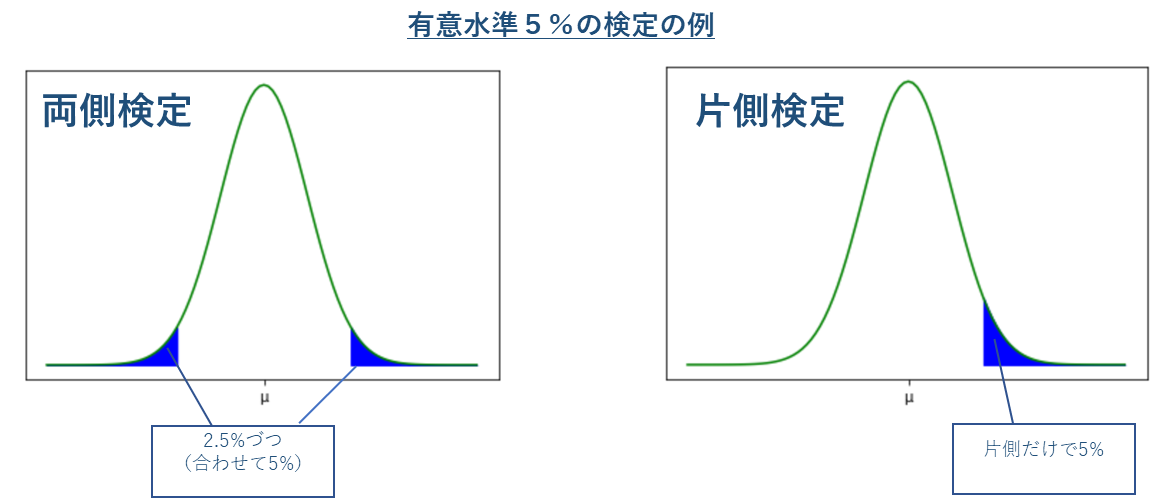
両側検定と片側検定

有意水準には、両裾の確率を合わせて α とする両側検定と、片裾の確率だけで α とする片側検定とがある。

【テストでのヒント】
一般的に「帰無仮説に差が無い ( ≒ )、対立仮説に差がある(≠）」とおいた場合は両側検定に、「帰無仮説に差がある (≦, ≧)、対立仮説にそれぞれ( >, <）」とおいた場合は片側検定となる。

有意水準、第１種過誤、第２種過誤、検出力

判断	帰無仮説 H₀が正しい	対立仮説 H₁が正しい
H₀を棄却	第１種過誤（有意水準: α）	正しい判断（検出力: 1 - β）
H₀を受容	正しい判断	第２種過誤（β）

5　１標本問題

①母平均の推定、検定

【区間推定】

\mu \hspace{5mm}= \hspace{5mm}\bar{x} \hspace{5mm}\pm\hspace{5mm} z_\alpha \frac{\sigma}{\sqrt{n}}

【仮説検定】

母分散が既知の場合＝Z検定

z \hspace{5mm}= \hspace{5mm} \sqrt{n}\frac{\bar{x} - \mu}{\sigma} \hspace{10mm} \sim \hspace{5mm}N(0, 1)

母分散が未知の場合＝t検定

t \hspace{5mm}= \hspace{5mm} \sqrt{n}\frac{\bar{x} - \mu}{\hat{\sigma}} \hspace{10mm} \sim \hspace{5mm}t(n-1)

　　　　　　　　　　　　※(n-1)は t 分布の自由度

②母分散の推定、検定

【区間推定】

\sigma^2  \hspace{5mm} = \hspace{5mm}\frac{(n-1)\hat{\sigma}^2}{\chi^2}

【仮説検定】

・χ²検定

\chi^2  \hspace{5mm} = \hspace{5mm} \frac{\sum({x} - \bar{x})^2}{\sigma^2}  \hspace{5mm} = \hspace{5mm} \frac{(n - 1)\hat{\sigma^2}}{\sigma^2}  \hspace{5mm} \sim \hspace{5mm}\chi^2(n-1)

　　　　　　　　　　　　　　　　　※(n-1)は χ² 分布の自由度

③母比率の推定、検定

【区間推定】

p  \hspace{5mm} =  \hspace{5mm}\hat{p}  \hspace{5mm} \pm \hspace{5mm} z\sqrt\frac{\hat{p}(1 - \hat{p})} {n}

【仮設検定】

・Z検定

z  \hspace{5mm} = \hspace{5mm} \sqrt{n} \hspace{1mm} \frac{\hat{p} - p}{\sqrt{p \hspace{1mm} (1 - p)}}  \hspace{5mm} \sim \hspace{5mm}N(0, 1)

６　2標本問題

①母平均の差の推定、検定

【区間推定】

母分散が既知の場合

\delta \hspace{5mm} = \hspace{5mm} d \hspace{3mm} \pm \hspace{3mm} z\hspace{2mm}\sqrt{\frac{\sigma_1^2}{m} + \frac{\sigma_2^2}{n}}  \hspace{5mm} \\
\hspace{3mm}*d = \bar{x} - \bar{y}

母分差が未知の場合

\delta \hspace{5mm} = \hspace{5mm} d \hspace{3mm} \pm \hspace{3mm} ｔ\times \sigma\hspace{2mm}\sqrt{\frac{1}{m} + \frac{1}{n} }   \hspace{10mm}\sim t(m+n-2)

対応のある２標本の場合（対標本）

\delta \hspace{5mm} = \hspace{5mm} \bar{d} \hspace{3mm} \pm \hspace{3mm} ｔ\times \frac{\hat{\sigma}}{\sqrt{n}}    \hspace{10mm}\sim t(n-1) \\
\hspace{5mm}*\bar{d} は d の平均

【仮説検定】

母分散が既知 -> Z検定

z \hspace{5mm} = \hspace{5mm} \frac{d - \delta}{\sqrt{\frac{1}{m} + \frac{1}{n}}\hspace{2mm} \sigma} \hspace{10mm} \sim N(0, 1)

母分散が未知 -> t検定

t \hspace{5mm} = \hspace{5mm} \frac{\bar{x} - \bar{y}}{\sqrt{\frac{\sigma_1^2}{m} + \frac{\sigma_2^s}{n}}\hspace{2mm} } \hspace{10mm} \sim t(m+n-2)

または、

t \hspace{5mm} = \hspace{5mm} \frac{\bar{x} - \bar{y}}{\sqrt{\frac{1}{m} + \frac{1}{n}}\hspace{2mm} \hat{\sigma} \hspace{2mm} } \hspace{10mm} \sim t(m+n-2) \\

\color{gray}{\astここで\, \hat{\sigma} \,は、プールされた分散を表す}

\hat{\sigma}^2 \hspace{5mm} = \hspace{5mm}  \frac{(m-1)\hat{\sigma}_1^2 + (n-1)\hat{\sigma}_2^2}{m+n-2}

②母分散の比の区間推定、検定

【区間推定】

F \hspace{5mm} = \hspace{5mm} \frac{\frac{W_1}{(m - 1)}}{\frac{W_2}{(n - 1)}}

F \hspace{5mm} = \hspace{5mm} \frac{\hat{\sigma_x^2}}{\sigma_x^2} ・ \frac{\sigma_y^2}{\hat{\sigma_y^2}}  \hspace{10mm}\sim F(m - 1, n - 1)

自由度(m - 1, n - 1) における上限 100α/2 %点（α はF分布の上限確率 ex. 0.05 )である F_α/2(m - 1, n - 1) と、下限 100α/2 %点である F_1-α/2(m - 1, n - 1) を用いて、母分散の比 σ²_y / σ²_xの信頼区間 100(1 - α)%の信頼区間は以下となる。

[\hspace{2mm} F_{1-α/2} (m - 1, n - 1) \frac{\hat{\sigma_y^2}}{\sigma_x^2} \hspace{5mm}, \hspace{5mm}F_{α/2} (m - 1, n - 1) \frac{\hat{\sigma_y^2}}{\sigma_x^2} \hspace{2mm}]

ここで、自由度(m1, m2)のF分布での上限 100(1-α/2) %点の値は、自由度(m2. m1)のF分布の条件 100α/2 %点の逆数（ F_1-α/2(m1, m2) = 1/F_α/2(m2, m1))である。

【仮説検定】

帰無仮説 H₀ のもとでは、

F \hspace{5mm} = \hspace{5mm} \frac{\hat{\sigma_x^2}}{\sigma_x^2} ・ \frac{\sigma_y^2}{\hat{\sigma_y^2}} \hspace{5mm}=\hspace{5mm}   \frac{\hat{\sigma_x^2}}{\hat{\sigma_y^2}}

であるので、

F_{1 - \alpha/2} (m - 1, n - 1) \leq F \leq F_{\alpha/2} (m - 1, n - 1)

であれば帰無仮説を受領し、そうでなければ棄却する。

③母比率の差の区間推定、検定

【区間推定】

p_1 - p_2 \hspace{2mm}=\hspace{2mm} \hat{p_1} - \hat{p_2} \hspace{5mm} \pm \hspace{5mm} Z_{\alpha/2} \sqrt{\frac{\hat{p_1}(1 - \hat{p_1)}}{n_1} + \frac{\hat{p_2}(1 - \hat{p_2)}}{n_2}} \\

* \sqrt{\hspace{3mm}} \hspace{2mm}の中は未知のp1, p2を推定値 \hat{p_1}、\hat{p_2}で置き換えている
*

【仮説検定】

zが近似的に標準正規分布に従うことを利用して仮説の検定を行う。

z \hspace{5mm}=\hspace{5mm} \frac{(\hat{p_1} - \hat{p_2}) - (p_1 - p_2)}{\sqrt{\frac{\hat{p_1}(1 -  \hat{p_1})}{n1} +  \frac{\hat{p_2}(1 -  \hat{p_2})}{n2}}}

なお、帰無仮説 H₀ : p1 = p2 (2つの標本の母比率に差はない）の元では以下の式となる。

z \hspace{5mm}=\hspace{5mm} \frac{\hat{p_1} - \hat{p_2}}{\sqrt{\frac{\hat{p_1}(1 -  \hat{p_1})}{n1} +  \frac{\hat{p_2}(1 -  \hat{p_2})}{n2}}}

７　線形回帰

７.１線形単回帰

y \hspace{5mm}=\hspace{5mm} \alpha \hspace{2mm}+\hspace{2mm} \beta x_i \hspace{2mm}+\hspace{2mm} \epsilon_i , \hspace{10mm}  \epsilon_i 〜 N(0,\sigma^2)

で表さられるモデルを線形単回帰モデル（単回帰モデル）と呼ぶ。２つ以上の説明変数（x）の場合は線形重回帰モデル（重回帰モデル）と呼ぶ。

単回帰モデルでの回帰係数 α、 β の推定量 α^{^} 、β^{^} は以下となる。

\hat{\beta}\hspace{5mm}=\hspace{5mm} \frac{T_{xy}}{T_{xx}}  \hspace{5mm} 〜\hspace{5mm}N(\beta,\frac{\sigma^2}{T_{xx}}) \\

\hat{\alpha}\hspace{5mm}=\hspace{5mm}\bar{y} \:-\: \hat{\beta}\bar{x} \\

ここで、 \\
T_{xy} \hspace{5mm}=\hspace{5mm} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \\

T_{xx} \hspace{5mm}=\hspace{5mm} \sum_{i=1}^{n} (x_i - \bar{x})^2 \hspace{15mm}

期待値と分散

E[\bar{\beta}] \hspace{5mm}=\hspace{5mm} \beta

V[\bar{\beta}] \hspace{5mm}=\hspace{5mm} \frac{\sigma^2}{T_{xx}}

誤差項 ε_i の分散 σ²の推定値

\hat{\sigma_2} \hspace{5mm}=\hspace{5mm} \frac{1}{n - 2} \sum_{i=1}^n (y_i - \hat{y_i})^2

　　　ここで、

\sum_{i=1}^n (y_i - \hat{y_i})^2 \hspace{2mm}=\hspace{2mm} T_{yy} - \hat{\beta}T_{xy} \hspace{2mm}=\hspace{2mm} (n -1) \cdot (\hat{\sigma}_y^2 - \beta\hat{\sigma}_{xy})

z 及び t値

z \hspace{5mm}=\hspace{5mm} \frac{\hat{\beta} - \beta}{\frac{\sigma}{\sqrt{T_{xx}}}} \hspace{5mm}〜\hspace{5mm} N(0,1) \\

t \hspace{5mm}=\hspace{5mm} \frac{\hat{\beta} - \beta}{\frac{\hat{\sigma}}{\sqrt{T_{xx}}}} \hspace{5mm}〜\hspace{5mm} t(n - 2)

β^の信頼区間

\hat{\beta} - t_{\alpha /2} (n - 2) \frac{\hat{\sigma}} {\sqrt{T_{xx}}} \hspace{5mm}\leq\hspace{5mm} \beta \hspace{5mm}\leq\hspace{5mm}  \hat{\beta} + t_{\alpha /2} (n - 2) \frac{\hat{\sigma}} {\sqrt{T_{xx}}} \\

\color{gray}{\ast: t_{\alpha /2} (n - 2)は、自由度 n - 2 の t 分布から上限 100α/2\%点を表す}

７.２線形重回帰　

総平方和

S_T（総平方和）\hspace{2mm}=　\hspace{2mm} S_R（回帰による平方和）\hspace{1mm}+\hspace{1mm} S_e(残差平方和） \\

自由度:　 n - 1 \hspace{5mm}=\hspace{5mm} p \hspace{15mm} + \hspace{5mm} (n - p - 1) \hspace{20mm}

\sum_i (y_i - \bar{y})^2  \hspace{5mm}=\hspace{5mm} \sum_i (\hat{y_i} - \bar{y})^2　\hspace{5mm} + \hspace{5mm} \sum_i (y_i - \hat{y_i})^2

自由度調整済み決定係数 R^*2 (Adjusted R-squared)
異なる説明変数を用いた重回帰モデル間でモデルの良し悪しを比較するために用いる係数。

R^{*2} \hspace{5mm}=\hspace{5mm}  1 \hspace{5mm}-\hspace{5mm} \frac{\frac{S_e}{(n - p - 1)}}{\frac{S_T}{(n - 1)}}   \\
  \hspace{10mm}  =  \frac{\frac{S_R}{p}}{\frac{S_T}{(n - 1)}}  \\
\color{gray}{\ast p は説明変数の数}

重回帰モデルの分散分析表

変動要因	平方和	自由度	平均平方	F
回帰	S_R	p	V_R = S_R / p	F = V_R / V_e
残差	S_e	(n - 1) - p	V_e = S_e / (n - 1 - p)
合計	S_T	n - 1

✳︎単回帰モデルの場合は上記表で p = 1 とすればよい

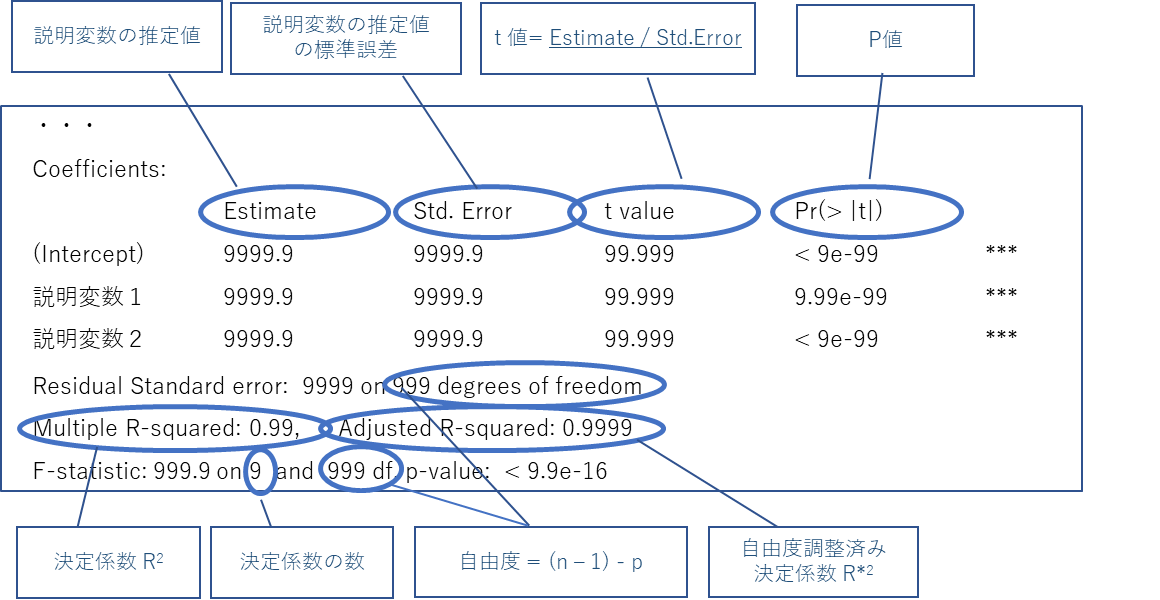
Rで回帰分析した際の出力レポートの見方

【テストでのヒント】
・上述のとおり異なる説明変数間でのモデルの比較は、自由度調整済み決定係数（R^*2)を用いる
・また、自由度調整済み決定係数（R^*2)の計算式、F値の算出式も覚えておく

８分散分析モデル

３つ以上の水準（３群以上）の平均の差についてF検定を実施し、ある要因（因子）が実験結果に影響を与えといってもよいかどうかを統計学的に検討する手法を分散分析という(t検定やF検定は２群を対象にした検定対象）。
ある１つの要因への影響を分析するのを「一元配置分散分析」と言い、２要因の場合は「二次元配置分散分析」、３要因以上の場合は多次元配置分散分析という。　ここでは「一元配置分散分析」を記載する。

水準	水準でのデータ数	観測値	平均
A₁	n₁	y₁₁,y₁₂,・・・,y_1n₁	y^-_1.
A₂	n₂	y₂₁,y₂₂,・・・,y_2n₂	y^-_2.
・・・	・・・	・・・	・・・
A_a	n_a	y_a1,y_a2,・・・,y_{an_a}	y^-_a.
	n		y^-..

総平方和（S_T）　\hspace{2mm}=\hspace{2mm} 水準間平方和（S_A） + 残差平方和（S_e）

自由度:　 n - 1 \hspace{10mm}=\hspace{2mm} ( a - 1 ) \hspace{2mm}+\hspace{2mm} (n - a) \hspace{15mm}

\sum_{j=1}^{a} \sum_{i=1}^{n_j}(y_{ji} - \bar{y}_{..})^2 = \sum_{j=1}^an_j(\bar{y}_{j.} - \bar{y}_{..})^2  +  \sum_{j=1}^{a} \sum_{i=1}^{n_j}(y_{ji} - \bar{y}_{j.})^2

１元配置の分散分析表

変動要因	平方和	自由度	平均平方(V)	F	E(V)
水準間	S_A	Φ_A = a - 1	V_A = S_A / Φ_A	V_A / V_e	σ² + Σ n_jα²_j / Φ_A
残差	S_e	Φ_e = n - a	V_e = S_e / Φ_e		σ²
合計	S_T	Φ_T = n - 1

【テストでのヒント】
上記の式(S_T = S_A + S_e)はテストで出題されることが多いので覚えておく。
自由度で見ると、n - 1 = (a - 1) + (n - a) であり、 n は全量なので y_ji 、a は水準間なので y_j. 、1 は全体の平均なので y_.. とすると覚えやすい。

９　ノンパラメトリック手法

特定の分布を仮定できないデータに対して検定を行う手法（正規分布などの分布を前提とするt検定やF検定はパラメトリック手法と呼ばれる）。

９.１　適合度の検定と独立性の検定(ピアソンの χ² 検定）

いわゆる母集団の分布に正規性が仮定できない場合に使用するノンパラメトリック手法の１つ。
適合度の検定は、理論上の確率分布から得られる「期待度数」と観測値の「度数」の当てはまりの良さを検定する。　独立性の検定は、クロス集計表の列項目と行項目間に関連性があるのかを「度数」から検定する。

✳︎ピアソンの χ² は、本来の χ² とは厳密には異なるが近似値的には従う。また、平均値や分散などの母数は使わず「度数」のみから検定統計量を求めることができる。

適合度の検定

	A₁ A₂　・・・ A_k	計
観測度数	O₁ O₂　・・・ O_k	n
期待度数	E₁ E₂　・・・ E_k	n

✳︎ E_i = np_i 、p_i は A_i に対する理論上の確率

ピアソンの χ² は以下の式となる。

\chi^2 \hspace{5mm}=\hspace{5mm} \sum_{i=1}^k \frac{(観測度数_i - 期待度数_i)^2}{\hspace{15mm}期待度数_i\hspace{15mm}}　　\hspace{5mm}〜\hspace{5mm} \chi^2(k - 1)

独立性の検定

クロス集計表から期待度数 -> χ² 値を計算する。　
以下に計算順序を例を用いて記載する。

クロス集計表（観測度数）

	賛成	どちらでもない	反対	行計
男	5	10	15	30①
女	10	5	5	20②
列	15③	15④	20⑤	50⑥

✳︎上記①〜⑥は下記期待度数の計算で使う番号

期待度数

	賛成	どちらでもない	反対	行計
男	⑥ × ①/⑥ × ③/⑥ = 9	⑥ × ①/⑥ × ④/⑥ = 9	⑥ × ①/⑥ × ⑤/⑥ = 12	30
女	⑥ × ②/⑥ × ③/⑥ = 6	⑥ × ②/⑥ × ④/⑥ = 6	⑥ × ②/⑥ × ⑤/⑥ = 8	20
列	15	15	20	50

ピアソンの χ² は以下の式となる。

\chi^2 \hspace{2mm}=\hspace{2mm} \sum_{i=1}^{行数}　\sum_{j=1}^{列数} \frac{(観測度数_{ij} - 期待度数_{ij})^2}{\hspace{15mm}期待度数_{ij}\hspace{15mm}}　　\hspace{5mm}〜\hspace{2mm} \chi^2(行数 - 1)(列数 - 1 )

ピアソンの χ² 値

	賛成	どちらでもない	反対	行計
男	(5 - 9)² / 9 = 1.78	(10 - 9)² / 9 = 0.11	(15 - 12)² / 12 = 0.75	2.64
女	(10 - 6)² / 6 = 2.67	(5 - 6)² / 6 = 0.17	(5 - 8)² / 8 = 1.13	3.96
列	4.44	0.28	1.88	6.60

∴ χ² = 6.60 となる。　また、自由度は行２×列３であるので、(2 - 1)× (3 - 1) = 2　となる。
あとは、通常の χ² と同様に検定を行う。

【テストでのヒント】
適合度及び独立性の検証の計算は確実にできるようにする

１０　おわりに

本書が統計学基礎の理解の促進、及び統計検定２級取得のお役に立てれば幸いです。

また、NPO法人AI開発推進教会では、さまざまなディープラーニングのモデルの解説書を作成して公開しています。
ディープラーニングにもご興味がありましたらご参照ください。

これから学ぶ人向け「統計検定２級」チートシート

１ 確率分布

１.１ 離散型確率分布

２項分布（Binomial Distribution）

ポアソン分布（Poisson Distribution）

幾何分布（Geometric Distribution)

１.２ 連続型確率分布

一様分布（Uniform Distribution）

正規分布（Normal Distribution）

指数分布（Exponential Distribution）

１.３ 歪度と尖度

１.４ 確率分布のまとめ

２ 確率のおさらい（補足）

２．１ 各種公式

２.２ 期待値と分散

２．３ 確率変数の公式

３ 標本分布

３．１ 母集団、標本、不偏推定量

３．２ t 分布

３．３ χ２分布

３．４ F分布

３．５ その他

大数の法則（law of large numbers）

中心極限定理（central limit theorem）

フィッシャーの３原則（Fisher's three principle）

標本抽出方法

４ 統計的推定と仮説検定

４.１ 仮設検定の構造

両側検定と片側検定

有意水準、第１種過誤、第２種過誤、検出力

5 １標本問題

①母平均の推定、検定

②母分散の推定、検定

③母比率の推定、検定

６ 2標本問題

①母平均の差の推定、検定

②母分散の比の区間推定、検定

③母比率の差の区間推定、検定

７ 線形回帰

７.１ 線形単回帰

期待値と分散

誤差項 εi の分散 σ2の推定値

z 及び t値

β^の信頼区間

７.２ 線形重回帰

８ 分散分析モデル

１元配置の分散分析表

９ ノンパラメトリック手法

９.１ 適合度の検定と独立性の検定(ピアソンの χ2 検定）

適合度の検定

独立性の検定

１０ おわりに

１確率分布

１.１離散型確率分布

１.２　連続型確率分布

１.３　歪度と尖度

１.４　確率分布のまとめ

２　確率のおさらい（補足）

２．１　各種公式

２.２　期待値と分散

２．３　確率変数の公式

３　標本分布

３．１　母集団、標本、不偏推定量

３．２　t 分布

３．３　χ^２分布

３．４　F分布

３．５　その他

４　統計的推定と仮説検定

４.１　仮設検定の構造

5　１標本問題

６　2標本問題

７　線形回帰

７.１線形単回帰

誤差項 ε_i の分散 σ²の推定値

７.２線形重回帰　

８分散分析モデル

９　ノンパラメトリック手法

９.１　適合度の検定と独立性の検定(ピアソンの χ² 検定）

１０　おわりに