tensorflowで交代級数を求めてみた #Python

最近tensorflowの勉強を始めたので交代級数を求めてみました。
間違っていたりしたらコメントをください。

目的

\sum^{\infty}_{n=1}(-1)^{n-1}/n\ \ が \log{2}\ へ収束するのかが知りたい.

この数式は区分求積法などを使えば証明できます。(詳しくは参考文献へ)

実行環境

os: windows10(Docker)
dockerイメージ: b.gcr.io/tensorflow/tensorflow:latest-devel
python: 2.7
virtualbox(docker machine): メモリ4gb(1gbでも問題ないと思います), プロセッサー4(1でも問題ないと思います)

実行方法

$ docker run -v [windows上の実行したいコードがあるディレクトリ]:/app -it b.gcr.io/tensorflow/tensorflow:latest-devel bash
# cd /app
# python alternating_sum.py

-vオプションでホストとコンテナのファイルを共有することができます。
詳しくはDocker公式を読んでください。

実装

alternating_sum.py

# coding:utf-8

import tensorflow as tf
import numpy as np
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt

N = 50000

# グラフ用
figy = np.zeros([21])
figdif = np.zeros([21])

# 変数などの設定
y = tf.Variable(tf.cast(0, tf.float32))
x = tf.placeholder(tf.float32)

# オペレーション
update_y = tf.assign(y, tf.add(y, tf.div(tf.cast(1, tf.float32), x)))

# log2との誤差
dif = tf.sub(tf.log(tf.cast(2, tf.float32)), y)

# sessionの初期化
sess = tf.Session()
sess.run(tf.initialize_all_variables())

# 計算開始
i = 0
for _ in range(N):
    i += 1
    tmp = -i if i % 2 == 0 else i

    sess.run(update_y, feed_dict={x: tmp})
    if i <= 20:
        figy[i] = sess.run(y)
        figdif[i] = sess.run(dif)
    if i % 10 == 0:
        print('STEP: %d, RES: %f, DIF: %f' %(i, sess.run(y), sess.run(dif)))

# グラフの作成
plt.plot(figy, label = "result")
plt.plot(figdif, label = "dif")
plt.legend()
plt.ylim([-2,2])
plt.savefig("result.png")

説明

y = tf.Variable(tf.cast(0, tf.float32))

初期の変数を0としています。tf.castがないとTypeErrorを起こします。

x = tf.placeholder(tf.float32)

xには 1 や -2 などの値が入ります。

update_y = tf.assign(y, tf.add(y, tf.div(tf.cast(1, tf.float32), x)))

tf.divで1/xを求めて、tf.addでy+tf.divを求める。
その値をtf.assignでyに代入する１行となります。
つまり、y = y + 1/x となります。
update_yはそれを行う演算子と思ってください。

dif = tf.sub(tf.log(tf.cast(2, tf.float32)), y)

log2とyの差を取っています。
log2の値はtensorflowの関数を使っています。

sess.run(tf.initialize_all_variables())

各変数の初期化を行っています。

for文

sess.runで実際に計算をすることになります。ここで y などの変数を引数に渡すと現在の y の値が返ってきます。
feed_dictで先ほど宣言したxに値をいれることをしています。

以上より目的である数式の結果を求めています。
グラフに関しては参考文献を読んでください。

結果

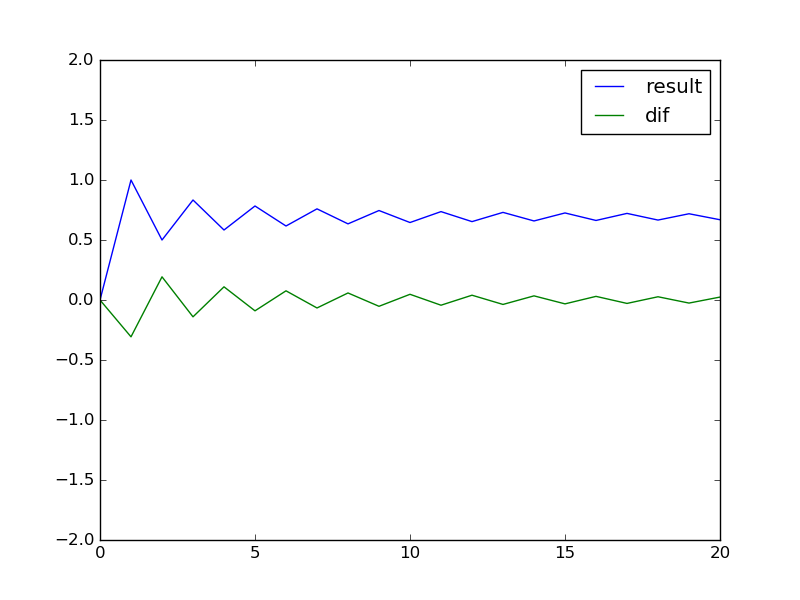
画像の結果

ターミナルへの出力結果

見やすくするため少し加工しました。
数値はいじってないです。

STEP: 1,     RES: 1.000000, DIF: -0.306853
STEP: 2,     RES: 0.500000, DIF:  0.193147
STEP: 3,     RES: 0.833333, DIF: -0.140186
STEP: 4,     RES: 0.583333, DIF:  0.109814
STEP: 5,     RES: 0.783333, DIF: -0.090186
STEP: 6,     RES: 0.616667, DIF:  0.076481
STEP: 7,     RES: 0.759524, DIF: -0.066377
STEP: 8,     RES: 0.634524, DIF:  0.058623
STEP: 9,     RES: 0.745635, DIF: -0.052488
STEP: 10,    RES: 0.645635, DIF:  0.047512
STEP: 100,   RES: 0.688172, DIF:  0.004975
STEP: 1000,  RES: 0.692646, DIF:  0.000501
STEP: 10000, RES: 0.693092, DIF:  0.000055
STEP: 50000, RES: 0.693129, DIF:  0.000018

最後に

tensorflowはディープランニングなどでよく使われると思いますが、今回は単純な数値計算を行いました。
色々つまずいた点もありましたが、tensorflowで作っていて楽しかったです。
tensorflowはいいぞ！

tensorflowで交代級数を求めてみた

目的

実行環境

実行方法

実装

説明

結果

画像の結果

ターミナルへの出力結果

最後に

参考文献

インターネット

書籍