はじめに
高校化学で登場する化学反応式も、微分方程式の力を借りて時間変化を見ることができます。今回は、化学物質濃度の時間変化を数式化し、グラフで描画、グラフがその形となる理由を説明していきます。
【動作環境】
MacOS Sierra 10.12.6
gnuplot 5.0 patchlevel 6
化学反応速度
化学物質AがBに変化していく、という状況を考えます。この場合の化学反応式は
A \xrightarrow{k} B
となります。ここで化学反応定数をkとしました。ここで、2つの化学物質の濃度[A],[B]がどのように変化していくかを見ていきます。
物質Aが減っていく速度は、元々Aがどれほどあったかに比例することが実験等でわかるので反応速度$V_A$は
V_A = -k[A]
と書くことができます。なお、Aは減少していくので符号はマイナスです。一方、物質Bが増えていく速度$V_b$は、Aが減った分増えるので$V_A$の正負を逆にした形
V_B = k[A]
として表現できます。
微分方程式の出番
「微分」を用いると、モノの単位時間当たりの変化量を見ることができました。これを使って、上の反応速度を微分方程式で書き直します。なお、濃度[A],[B]をa(t),b(t)と表現します。
(1.1)\qquad\left\{
\begin{align*}
\dfrac{da}{dt}&=-ka(t)\\
\dfrac{db}{dt}&=ka(t)
\end{align*}
\right.
可視化
濃度$a(t),b(t)$がどのように変化しているかグラフを求めてみます。
ここでは、初期値$a(0)=100,b(0)=0,k=0.5$とします。今回は近似計算法としてEuler法を用いていますが、詳細はこちらで解説していますので、参照してください。
# include <stdio.h>
//初期値、反応速度定数を定義しておく
# define init_a (1)
# define init_b (0)
# define k (0.5)
double systemA(double);
int main(int argc, const char * argv[])
{
//ファイル出力コマンド
FILE *fp;
FILE *gnu;
char *fname = "chem.csv";
fp = fopen(fname, "w");
int i;
//時間
double T = 20.0;
//ステップ数
int m = 10000;
//ステップ幅
double h = T / (double)m;
//求めたい値
double a,b;
//初期値
double a0 = init_a, b0 = init_b;
//初期値のセット
a=a0, b=b0;
//行名と初期値をエクセルファイル"SIRmodel.csv"に出力
fprintf(fp, "time, a(t), b(t) \n");
fprintf(fp, "0.0 , %lf , %lf \n", a, b);
//Euler法で計算
for(i=1; i<=m; i++)
{
a = a + h * systemA(a);
b = b + h * -systemA(a);
//計算結果をエクセルファイルに出力
fprintf(fp, "%lf, %lf, %lf\n", i*h, a, b);
}
gnu = popen ("gnuplot -persist -geometry 400x200+70+480", "w");
fprintf(gnu ,"plot \"chem.csv\" using 1:2 w l\n");
fprintf(gnu, "replot \"chem.csv\" using 1:3 w l\n");
pclose(gnu);
}
//反応速度式を関数として定義
double systemA(double a)
{
return -k * a;
}
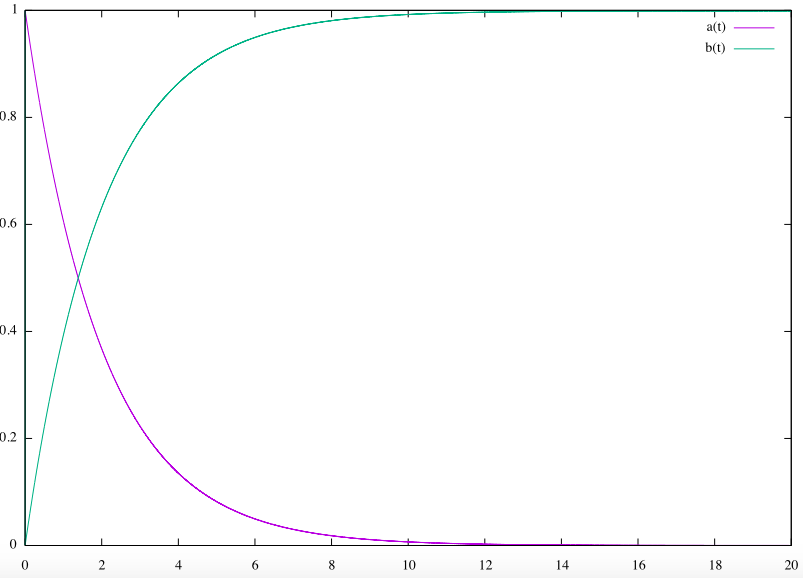
Aの濃度$a(t)$は指数関数的に単調に減少し、時刻t=20に近づくにつれて濃度も0へ近づいていきます。一方、Bの濃度$b(t)$は単調に増加し、時刻t=20に近づくにつれて濃度1へ近づいていきます。
なぜグラフのような挙動を描くのか
AとBの濃度が上のグラフのように変化することを微分方程式を用いて説明できます。
Aの濃度の変化は次の微分方程式で表されるのでした。
\dfrac{da}{dt}=-ka
これは、簡単に解くことができて、
a(t)=a(0)e^{-kt}
ここで、初期値a(0)=1でしたから
a(t)=e^{-kt}
です。この式から$a(t)$は、指数関数的に減少していくことがわかります。
では、$b(t)$はどうでしょう。式(1.1)の両辺を足すと
\dfrac{da}{dt}+\dfrac{db}{dt}=0
から
a(t)+b(t)=const.
つまり、総濃度数は時間変化しないということがわかります。したがって
a(t)+b(t)=a(0)+b(0)=1
から
b(t) = 1-a(t)
つまり
b(t) = 1-e^{-kt}
と求まりました。この式から$b(t)$は1に向かって指数関数的に上昇して行くことがわかります。
まとめ
*化学反応式の反応速度は微分方程式で表現できた
*Euler法を用いて化学物質濃度の時間変化をグラフ化して表現できた
*グラフの形は元の微分方程式から、数学的に説明できた