LoginSignup
4
2

More than 5 years have passed since last update.

@Dason08(Dason)

Modified-Euler法による数値計算法

Last updated at Posted at 2017-12-11

はじめに

微分方程式の中には紙とペンで簡単に解けるものと、そうでないものがあります。例えば

\dfrac{dx}{dt}=ax(t)

という微分方程式は$x(t)=x(0)e^{at}$と解けて、解$x(t)$の時間変化は指数関数的であることがすぐに分かります。しかし、簡単に解けない場合は近似計算を用いて、その解のだいたいの挙動を知ることができます。今回はEuler法から始め、Euler法より精度のよい近似計算法であるModified-Euler法の導入を行います。

【動作環境】

MacOS Sierra 10.12.6
gnuplot 5.0 patchlevel 6

Euler法

Euler法の導出

\dfrac{dx}{dt}=f(x)

という微分方程式をEuler法で数値計算してみましょう。まずは、微分の定義から。

\dfrac{dx}{dt}=\lim_{h\to 0}\dfrac{x(t+h)-x(t)}{h}

数値計算を実施するのはパソコンですから、パソコンには「極限」の計算はできません。ここでは、$lim_{h\to0}$を無視してみましょう。すると上の式は

\dfrac{dx}{dt}\sim \dfrac{x(t+h)-x(t)}{h}

となり、これを綺麗にすると

x(t+h)\sim x(t)+h f(x,t)

となります。ここで、時刻tに対して時刻t+hが１ステップ先であると考えると次のように書きかえることができます。

x_{t+1}\sim x_t+h f(x_t)

これがEuler法の核となる式です。

Euler法の実装

\dfrac{dx}{dt} = -y(t)\\
\dfrac{dy}{dt} = x(t)\\
x(0) = 1, y(0) = 0

これをEuler法で解きましょう。プログラムは次の通りです。

Euler.c
#include <stdio.h>

int main(int argc, const char * argv[])
{
    //ファイル出力コマンド
    FILE *fp;
    FILE *gnu;
    char *fname = "euler.csv";
    fp = fopen(fname, "w");

    int i;

    //時間
    double T = 100.0;

    //ステップ数
    int m = 10000;

    //ステップ幅
    double h = T / (double)m;

    //求めたい値
    double x,y;
    double xnext, ynext;

    //初期値
    double x0 = 1.0, y0 = 0.0;

    //初期値のセット
    x=x0, y=y0;

    //行名と初期値をエクセルファイル"SIRmodel.csv"に出力
    fprintf(fp, "time, x(t), y(t) \n");
    fprintf(fp, "0.0 , %lf , %lf  \n", x, y);

    //Euler法で計算
    for(i=1; i<=m; i++)
    {
        xnext = x + h * (-y);
        ynext = y + h * x;

        x = xnext;
        y = ynext;

        //計算結果をエクセルファイルに出力
        fprintf(fp, "%lf, %lf, %lf\n", i*h, x, y);  
    }

    gnu = popen ("gnuplot -persist -geometry 400x200+70+480", "w");
    fprintf(gnu ,"set size square\n");
    fprintf(gnu ,"set xrange [-2.0:2.0]\n");
    fprintf(gnu ,"set yrange [-2.0:2.0]\n");
    fprintf(gnu ,"plot \"euler.csv\" using 2:3 w l title 'Euler'\n");
    pclose(gnu); 
}

このプログラムのEuler法の部分に注目してみましょう。


//Euler法で計算
    for(i=1; i<=m; i++)
    {
        xnext = x + h * (-y);
        ynext = y + h * x;

        x = xnext;
        y = ynext;
     }

1つ目のEuler法の式における右辺$x_t+hf(x_t)$は今回の場合、元の微分方程式から$x'(t)=-y$だから$f(x_t)=-y$なので、

x_{t+1} = x_t + h (-y_t)

となります。全く同様に2つ目の式についても

y_{t+1} =y_t + h x_t

となります。
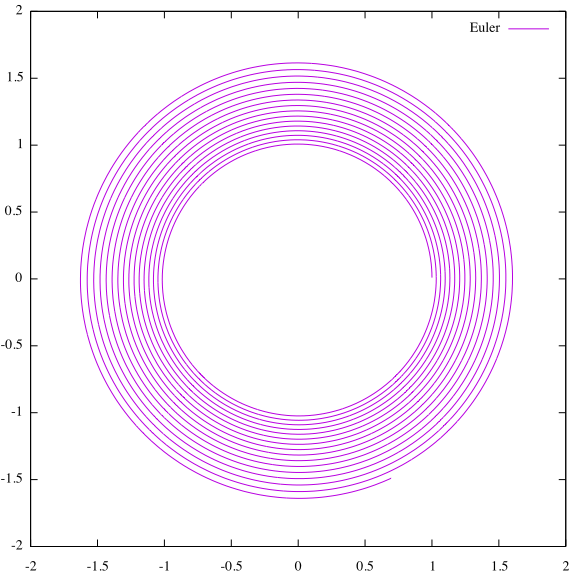
なお、このプログラムの出力は次のようになります。横軸x、縦軸yとした図を描いたので円状になりましたが、初期値$(x,y)=(1.0)から$だんだん外側へと広がって行くように見えます。本当にこれで正しいのでしょうか？

Euler.png

Modified-Euler法

Euler法からModified-Euler法へ

もう一度Euler法の式を見てみましょう。

x_{t+1}\sim x_t+h f(x_t)

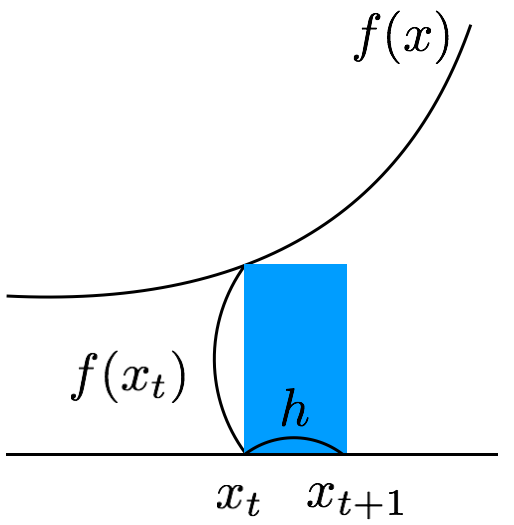
特に$hf(x_t)$に注目してみましょう。

M1.png

$x_t$と$x_{t+1}$の幅$h$と$f(x_t)$の掛け算、つまりは図の青い部分の面積を表現していることになります。
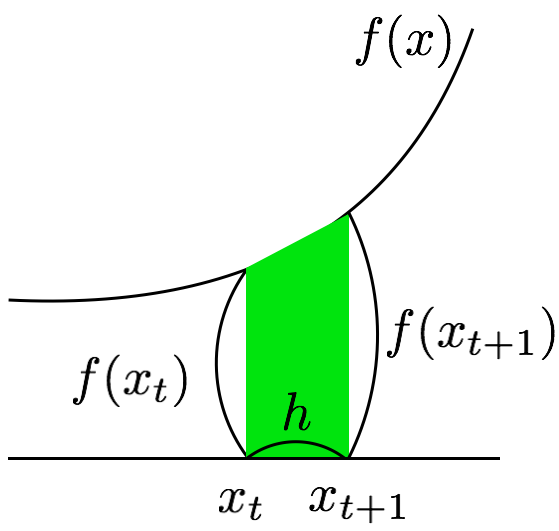
では、これを台形で近似することにしましょう。すると図は次のようになります。

M_E.png

これを式で表すと次のようにできます。

x_{t+1}\sim x_t+\dfrac{h}{2}\left\{ f(x_t)+f(x_{t+1})\right\}

この数式をじっと見ると時刻t+1の値を求めるには、時刻tの値と時刻t+1の値が必要になっています。「時刻t+1の値を求めるのに、時刻t+1の値を使う...？何を言ってるんだ？」と言いたくなりますが、ここで時刻t+1の値をEuler法を用いて近似することにしましょう。すると右辺の$x_{t+1}$が$x_t+hf(x_t)$で近似されるので

x_{t+1}\sim x_t+\dfrac{h}{2}\left\{ f(x_t)+f(x_t+hf(x_t))\right\}

とできます。これがModified-Euler法の核となる式です。

Modified-Euler法の実装

\dfrac{dx}{dt} = -y(t)\\
\dfrac{dy}{dt} = x(t)\\
x(0) = 1, y(0) = 0

先ほどと同じ式をModified-Euler法で解きましょう。プログラムは次の通りです。

Modified-Euler
#include <stdio.h>

int main(int argc, const char * argv[])
{
    //ファイル出力コマンド
    FILE *fp;
    FILE *gnu;
    char *fname = "modified-euler2.csv";
    fp = fopen(fname, "w");

    int i;

    //時間
    double T = 100.0;

    //ステップ数
    int m = 10000;

    //ステップ幅
    double h = T / (double)m;

    //求めたい値
    double x,y;
    double xnext, ynext;

    //初期値
    double x0 = 1.0, y0 = 0.0;

    //初期値のセット
    x=x0, y=y0;


    //modified-Eulerで計算する際に、途中で用いるEuler法の部分の値
    double k1,k2;

    //行名と初期値をエクセルファイル"SIRmodel.csv"に出力
    fprintf(fp, "time, x(t), y(t) \n");
    fprintf(fp, "0.0 , %lf , %lf  \n", x, y);


    //modified-Euler法で計算
    for(i=1; i<=m; i++)
    {
        k1 = x + h * (-y);
        k2 = y + h * x;

        xnext = x - h * (y + k2)/2;
        ynext = y + h * (x + k1)/2;

        x = xnext;
        y = ynext;

        //計算結果をエクセルファイルに出力
        fprintf(fp, "%lf, %lf, %lf\n", i*h, x, y);  
    }

    gnu = popen ("gnuplot -persist -geometry 400x200+70+480", "w");
    fprintf(gnu ,"set size square\n");
    fprintf(gnu ,"set xrange [-2.0:2.0]\n");
    fprintf(gnu ,"set yrange [-2.0:2.0]\n");
    fprintf(gnu ,"plot \"modified-euler2.csv\" using 2:3 w l title 'Modified-Euler'\n");
    pclose(gnu); 
}

ここで、Modified-Euler法で計算している部分に注目してみましょう。

//modified-Euler法で計算
    for(i=1; i<=m; i++)
    {
        k1 = x + h * (-y);
        k2 = y + h * x;

        xnext = x - h/2 * (y + k2);
        ynext = y + h/2 * (x + k1);

        x = xnext;
        y = ynext;
    }

k1とk2は、Euler法でそれぞれxとyを計算しています。プログラム中で$x$の次の時刻である$x_{next}$は、今現在の$f(x_t)=-y_t$とEuler法で計算した次の時刻の$f(x_{t+1})=-y_{t+1}=-k_2$を足し合わせたものに$\dfrac{h}{2}$をかけて

x_{t+1} = x_t - \dfrac{h}{2}(y_t + y_{t+1}) = x_t - \dfrac{h}{2}(y_t + k_2)

として表現されます。$y_{t+1}$についても同様に

y_{t+1} = y_t +\dfrac{h}{2}(x_t + x_{t+1}) = y_t + \dfrac{h}{2}(x_t + k_1)

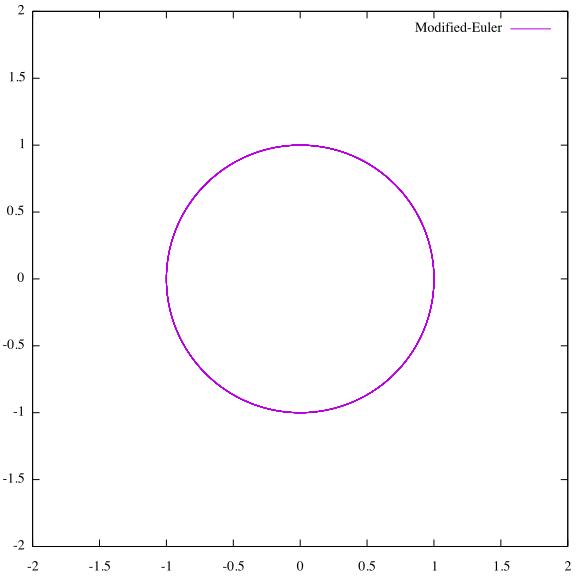
となります。このプログラムを実行した結果得られる出力は次のようになります。

Mod_Euler.png

先ほどのEuler法の出力と比較して、外に広がって行く様子は見られず丸い軌道を描いているように見えます。「Modified-Euler法」(修正オイラー法)というくらいですから、こちらの方が精度が高いはずです。最後に、与えられた微分方程式からModified-Euler法の軌道が実際の解の挙動に近いことを示してみましょう。

微分方程式の真の解軌道

\dfrac{dx}{dt} = -y(t)\\
\dfrac{dy}{dt} = x(t)\\
x(0) = 1, y(0) = 0

この微分方程式を行列/ベクトル表記すると次のように書くことができます。

\begin{eqnarray*}
\left(
\begin{array}{c}
x'(t)\\y'(t)
\end{array}
\right)
=
\left(
\begin{array}{cc}
0&-1\\1&0
\end{array}
\right)
\left(
\begin{array}{c}
x(t)\\y(t)
\end{array}
\right)
\end{eqnarray*}

実はこれは手計算で解くことができるので、実際に解いてみましょう。まず、便宜上

\begin{eqnarray*}
{A}=\left(
\begin{array}{cc}
0&-1\\1&0
\end{array}
\right)
\end{eqnarray*}

とおきます。この特性方程式が

det({A}-\lambda{E})=\lambda^2+1=0

となることから固有値が$\pm i$とわかります。ここから、積分定数$C_1,C_2$を用いて

\begin{eqnarray*}
\left(
\begin{array}{c}
x(t)\\y(t)
\end{array}
\right)
=
\left(
\begin{array}{c}
C_1\cos{t}+C_2\sin{t}\\C_2\cos{t}-C_1\sin{t}
\end{array}
\right)
\end{eqnarray*}

ここで初期値が

\begin{eqnarray*}
\left(
\begin{array}{c}
x(0)\\y(0)
\end{array}
\right)
=
\left(
\begin{array}{c}
1\\0
\end{array}
\right)
\end{eqnarray*}

ですから、与えられた微分方程式の解は

\begin{eqnarray*}
\left(
\begin{array}{c}
x(t)\\y(t)
\end{array}
\right)
=
\left(
\begin{array}{c}
\cos{t}\\-\sin{t}
\end{array}
\right)
\end{eqnarray*}

となりました。さて、ここで$x^2+y^2$を計算してみると、$x^2+y^2=\cos^2{t}+\sin^2{t}=1$ですから、微分方程式の解の挙動は

x^2+y^2=1

つまり、中心(0,0)、半径1の円であることがわかりました。
では、Euler法とModified-Euler法によって描かれた解の挙動をもう１度見てみましょう。
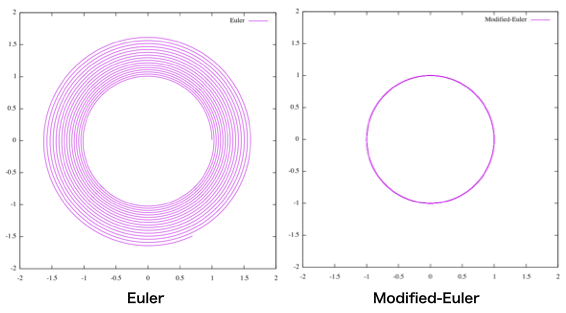
スクリーンショット 2017-12-11 14.39.04.png

より、実際の解である円に近い挙動をみせたのは、Modified-Euler法であることが一目瞭然ですね。近似計算の第１歩として学習するEuler法ですが、実際は誤差を多く含む近似アルゴリズムであるということがこれで理解できたと思います。また、Modified-Euler法も実装が簡単なのに、ある程度の精度は保証できそうですが、完璧ではなく少なからず誤差は含まれる手法ですので、研究等ではより精度の高い近似法を使うことが求められそうです。(数学を用いたEuler法とModified-Euler法の精度の説明ついてはこちらを参照してください。)

まとめ

＊Euler法とModified-Euler法の数値計算を実装してみた。
＊Euler法は大きな誤差を持っており、研究等には向いていないので他の手法が求められる。

4
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
2