競プロのライブラリ整理~BIT(Binary Indexed Tree)~

ABC107-D Median of Mediansにおいて、BIT(Binary Indexed Tree)を使う必要があったので、ネットで調べつつ実装しました。

BITを使ったのは今回が初めてなので、丁寧にBITについてまとめていきたいと思います。間違いなどがあったら教えてください。また、図についてはHCPCの勉強会のスライドを参考にさせていただきました。また、kamiさんの解説が発展的なものも取り扱っておりわかりやすいので、参考にしてみてください。

#BITとは？
BITとはBinary Indexed Treeの略で、数列の初めの要素からi番目までの区間和を求めるために使います。

BITはセグメント木の機能を限定したものであり、実装が簡単でメモリを節約できるなどの長所があります。

#BITの仕組み

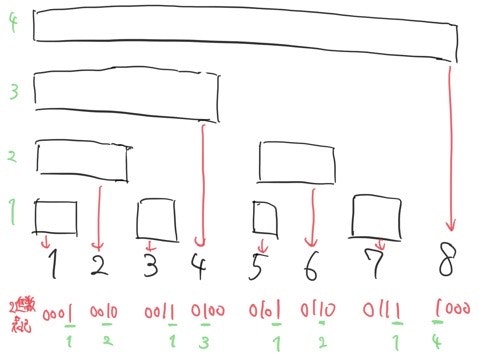
ここではわかりやすいように数列を$a_1,a_2,…,a_8$考えます。
すると、この配列において、以下のようにそれぞれの数列の要素に対応する部分の和を持ちます。

この図を見る限りでは部分の長さが2の倍数であることしかわかりませんが、LSB(Least Significant Bit)に注目するとわかりやすいです。LSBとは二進数で表現した時に初めて1が出てくるのは右から数えて何番目かというもので、上図においては区間の長さがLSBと対応します(緑の印をつけてあります。)。

#BITの機能

BITは先ほども述べたように、区間和の計算を高速に行います。また、値の更新を行うことももちろんでき、どちらの計算についても$O(\log{n})$の時間計算量で行うことができます。
ここでは、この二つの機能に絞って書いていこうと思います。

##BITでの区間和の計算

$a_1+a_2+…+a_i$という区間の和をBITでは$O(\log{n})$で求めることができます。

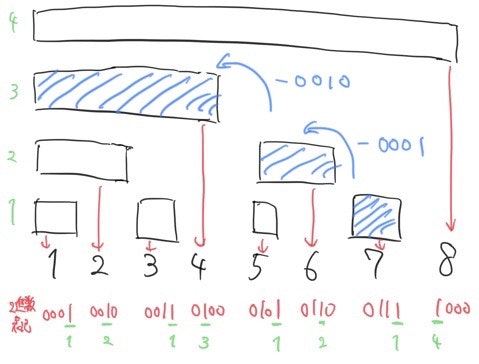
この計算はLSBの減算により行うことができます。$i=7$の時であれば以下のようになります。

減算される桁を赤で、減算された桁を青で表して挙動を示すと以下の表になります。また、その様子を図にしたものが以下の図になります。

7	0111
↓		↓ -0001
6	0110
↓		↓ -0010
4	0100
↓		↓ -0100
0	0000	←0になるまで

##BITでの値の更新

数列の要素$a_i$に$x$を足す操作をBITでは$O(\log{n})$でできます。

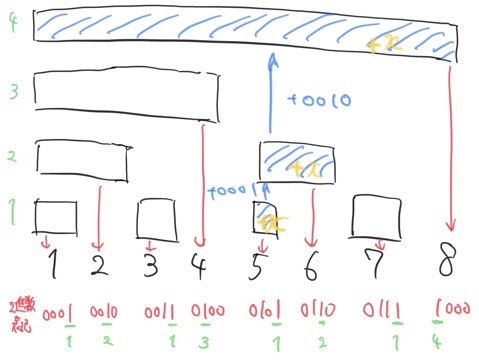
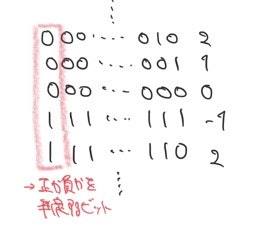
この計算はLSBの加算により行うことができます。$i=5,x=2$の時であれば以下のようになります。

加算される桁を赤で、加算された桁を青で表して挙動を示すと以下の表になります。また、その様子を図にしたものが以下の図になります。

5	0101
↓		↓ +0001
6	0110
↓		↓ +0010
8	1000	←nを超えない値まで

##BIT上での二分探索(2020/05/20追加)

先日出たCodeforcesにおいてBIT上での二分探索が必要な問題(問題はこちら)があり二分探索は実装していなかったので、復習として実装することにしました。

BIT上では$a_1+a_2+…+a_i>=x$となる最小の$i$を$O(log{n})$で求めることができます(ただし、数列aの全要素が0以上)。

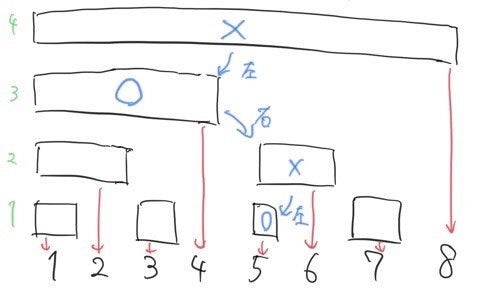
最小の$i$が5になる場合の二分探索の際の挙動は以下のようになります。
長い区間から順に辿っていってその区間を含めても合計が$x$未満の場合はその区間を含めて下の区間を探していきます。
これを繰り返して一番下の長さ1の区間までたどりついた時のインデックスの一つ隣が求める答えであるiになります。

#C++によるBITの実装

以下はクラスの中は1-indexedで関数に与える引数は0-indexedでの実装になり、先ほどまでで説明した内容をそのまま実装しています。

また、コード中のk & -kというコードがLSBを表しますが、説明を付与しました。

##BITのコード

BIT.cc

//数列a(a[0],a[1],…,a[n-1])についての区間和と点更新を扱う
//区間和,点更新,二分探索はO(log{n})で動作する
class BIT {
public:
    //データの長さ
    ll n;
    //データの格納先
    vector<ll> a;
    //コンストラクタ
    BIT(ll n):n(n),a(n+1,0){}

    //a[i]にxを加算する
    void add(ll i,ll x){
        i++;
        if(i==0) return;
        for(ll k=i;k<=n;k+=(k & -k)){
            a[k]+=x;
        }
    }

    //a[i]+a[i+1]+…+a[j]を求める
    ll sum(ll i,ll j){
        return sum_sub(j)-sum_sub(i-1);
    }

    //a[0]+a[1]+…+a[i]を求める
    ll sum_sub(ll i){
        i++;
        ll s=0;
        if(i==0) return s;
        for(ll k=i;k>0;k-=(k & -k)){
            s+=a[k];
        }
        return s;
    }

    //a[0]+a[1]+…+a[i]>=xとなる最小のiを求める(任意のkでa[k]>=0が必要)
    ll lower_bound(ll x){
        if(x<=0){
            //xが0以下の場合は該当するものなし→0を返す
            return 0;
        }else{
            ll i=0;ll r=1;
            //最大としてありうる区間の長さを取得する
            //n以下の最小の二乗のべき(BITで管理する数列の区間で最大のもの)を求める
            while(r<n) r=r<<1;
            //区間の長さは調べるごとに半分になる
            for(int len=r;len>0;len=len>>1) {
                //その区間を採用する場合
                if(i+len<n && a[i+len]<x){
                    x-=a[i+len];
                    i+=len;
                }
            }
            return i;
        }
    }
};

##k & -kがLSBになる理由

ここで-kはここでは負の数になりますが、負の数がコンピュータ上では補数表現されていることを考えれば-kの値がどうなるかは難しくありません。

補数表現は上記のように一番上のビットが1の場合を負の数として定義しています。すなわち、-k=~k+1になります(~はそれぞれのビットを反転するビット演算です)。

このもとで、kのLSBがk & -kになることを示します。
まず、kのLSBをxとすると、二進数表現での右から1~x-1番目は0で右からx番目は1になります。よって、~kの二進数表現での右から1~x-1番目は1で右からx番目は0になります。
したがって、-k=~k+1から繰り上がりを計算しながら-kを求めると、二進数表現での右から1~x-1番目は0で右からx番目は1になります。また、x番目より左側についてはkと-kのビットは全て異なります。
よって、k & -kにおいてkと-kのいずれもが1になるようなビットはx番目のみであり、kのLSBを得ることができています。

#BITによる転倒数の求め方

ABC107-D Median of Mediansにおいては転倒数と似た考え方で問題を解く必要があったので、転倒数の求め方についてもこの記事で扱おうと思います。

まず、転倒数とは、「数列$a_1 , a_2 ,…, a_n$がある時にi<jで$a_i>a_j$となる$(i,j)$の組の個数」のことです。

ここで、普通に転倒数を求めると、jを固定して($i$を固定しても良いですが説明の都合上$j$にします)、$i$:1→$j-1$で$a_i>a_j$が成り立つものを数え上げればよく、$O(n^2)$の計算量になります。

しかし、BITを使うと、「$i$:1→$j-1$で$a_i>a_j$が成り立つもの」の数え上げは$O(\log({a_{max}-a_{min}}))$へと計算量を落とすことができます(工夫すれば$O(\log{n})$まで計算量を落とすことができます。)。…(✳︎)

まず、BITを使うための前処理として全要素を1以上にする必要があり、これは$a_{min}=1$にすれば実現できるので、全要素に$1-a_{min}$を足す必要があります。この処理を行った後の配列を$b_1 ,b_2 ,…,b_n$とすれば$1 \leqq b_1 ,b_2 ,…,b_n \leqq a_{max}-a_{min}+1$が成り立ちます。

ここで、BITで管理する配列を$c_1,c_2,…,c_{a_{max}-a_{min}+1}$として、「$c_i$は$i$が何回現れたかを保存する」とすれば、$b_1 ,b_2 ,…,b_{k-1}$の中で$1,2,…,a_{max}-a_{min}+1$がそれぞれ何回現れたかを保存しておくことで、$b_k$を見た時に$c_{b_k+1}+c_{b_k+2}+…+c_{a_{max}-a_{min}+1}$が「$k$を固定した時に$b_j > b_k$となる$(j,k)$の組の総数」となります。

また、kを固定した時に$c_1+c_2+…+c_{a_{max}-a_{min}+1}=k-1$が成り立つので、$c_{b_k+1}+c_{b_k+2}+…+c_{a_{max}-a_{min}+1}=k-1-(c_1+c_2+…+c_{b_k})$が成り立ちます。

ここで、$c_1+c_2+…+c_{b_k}$はBITにおいて$O(\log({a_{max}-a_{min}}))$ので、(✳︎)であることが示されました。

コード例については、ABC107-D Median of Mediansと近いものになってしまうので省略しますが、気になる場合はいかたこさんの解説やkamiさんの解説を参考にしてください。