[1]前書き
この記事ではランレングス圧縮を紹介します。他の紹介している記事1$^,$2とは違い、Pythonでの実装及び問題の解説について詳しく書きました。
また、以下では問題の解説を載せているのでネタバレを含みます。解説を見ないで解きたい場合は[6]問題一覧から解いてください。
[2]ランレングス圧縮とは
ランレングス圧縮とは連続したデータを(値,連続する個数)として圧縮する可逆的データ圧縮アルゴリズムのことです。競技プログラミングでは主に文字列や数列などの連続するデータを圧縮するために用いられます。
また、以下では連続したデータのグループをまとめて扱いやすくするという意味でも"ランレングス圧縮"と記しますが、これは表記の統一のためで本来はグループ化や圧縮などと表記すべきです。
[3]ランレングス圧縮の実装
Pythonのitertoolsライブラリのgroupby関数を利用することで簡単にランレングス圧縮を行うことができます。具体的な使い方は以下のようになります。
例えば、[1, 1, 2, 2, 2, 4, 4, 4, 5]という配列があったとします。この配列にランレングス圧縮を行った時、定義に従えば[[1, 2], [2, 3], [4, 2], [5, 1]]のように[値,連続する個数]として圧縮をできれば良いです。従って、groupby関数によりランレングス圧縮を行えば以下のようになります。
>>> iterable=[1, 1, 2, 2, 2, 4, 4, 4, 5]
>>> [[key,len(list(group))] for key,group in groupby(iterable)]
[[1, 2], [2, 3], [4, 3], [5, 1]]
groupby関数の挙動を説明すると、同じキー(デフォルトでは恒等関数)を持つ連続するグループをまとめて(キー,グループ)の組にしてイテレータで返します。また、引数にはイテラブルを指定する必要があります。また、グループはitertools._groupberのオブジェクトとして返されるので、扱いやすいリストに変換するのが一般的です。そして、ランレングス圧縮では連続する個数(それぞれのグループの長さ)が分かれば良いので、リストの長さを返すようにすれば良いです3。
また、他にもitertoolsライブラリには便利な関数があるので、詳しくはPythonで競プロするのに必要な機能をまとめてみた~itertools~を見てください。
[4]問題での使用方法
ランレングス圧縮は競技プログラミングで主に以下の三つの使用方法があります。
(1)連続した部分をまとめて扱う
連続した部分をまとめて扱うことで連続した部分ごとでの考察に帰着することができます。また、連続した部分ごとに分けるのにgroupby関数を使うと簡単に書くことができます。
(2)変化する部分のみに着目する
連続した部分をまとめて扱うことでその連続部分の境界部(変化する部分)のみに注目した考察を行うことができます。例えば、極大値や極小値4を線形に探すことができます。
(3)データサイズを圧縮する
ランレングス圧縮の本来の使用方法ですが競技プログラミングだと少ないと思います。この場合はgroupby関数を用いることができませんが、ランレングス圧縮の考えを用いて解くことができます。
[5]問題での使用例
先程の3パターンについてそれぞれ使用例を載せます。特に重要なものについては記事中で解説をし、他のものについてもヒント及びコード中のコメントアウトで解説をしています。
(0)groupbyをそのまま使う
groupby関数をそのまま使うだけで解ける問題です。
・問題例
ABC019B 高橋くんと文字列圧縮
→ヒント:groupbyを使うだけです。文字列の扱いに注意してください。
→提出:https://atcoder.jp/contests/abc019/submissions/18651790
ABC047C 一次元リバーシ
→ヒント:一つ石を打った時の変化を考えてください。
→提出:https://atcoder.jp/contests/abc047/submissions/18651800
(1)連続した部分をまとめて扱う
「(0)groupby関数をそのまま使う」時と同様に連続した部分でまとめることで解ける問題です。
・問題例1(Codeforces #600(Div.2)A Single Push)
重要なのは、配列$d$を$d[i]:=b[i]-a[i]$としてgroupby関数を適用するとキーが0でない部分が高々一つで、一つ存在するときはそのキーが正であれば配列$b$に一致させることができる、という点です5。
また、以下のようにgroupbyのkey引数にlambda i:b[i]-a[i]を指定することで、配列$d$のキーが0でない部分を以下のコードで列挙することができます。そして、列挙することができれば残りは出力の条件分岐に気をつけるだけです。
c=[[key,group] for key,group in groupby(range(n),key=lambda i:b[i]-a[i]) if key!=0]
→提出:https://codeforces.com/contest/1253/submission/100802808
・問題例2(ABC182E Akari)
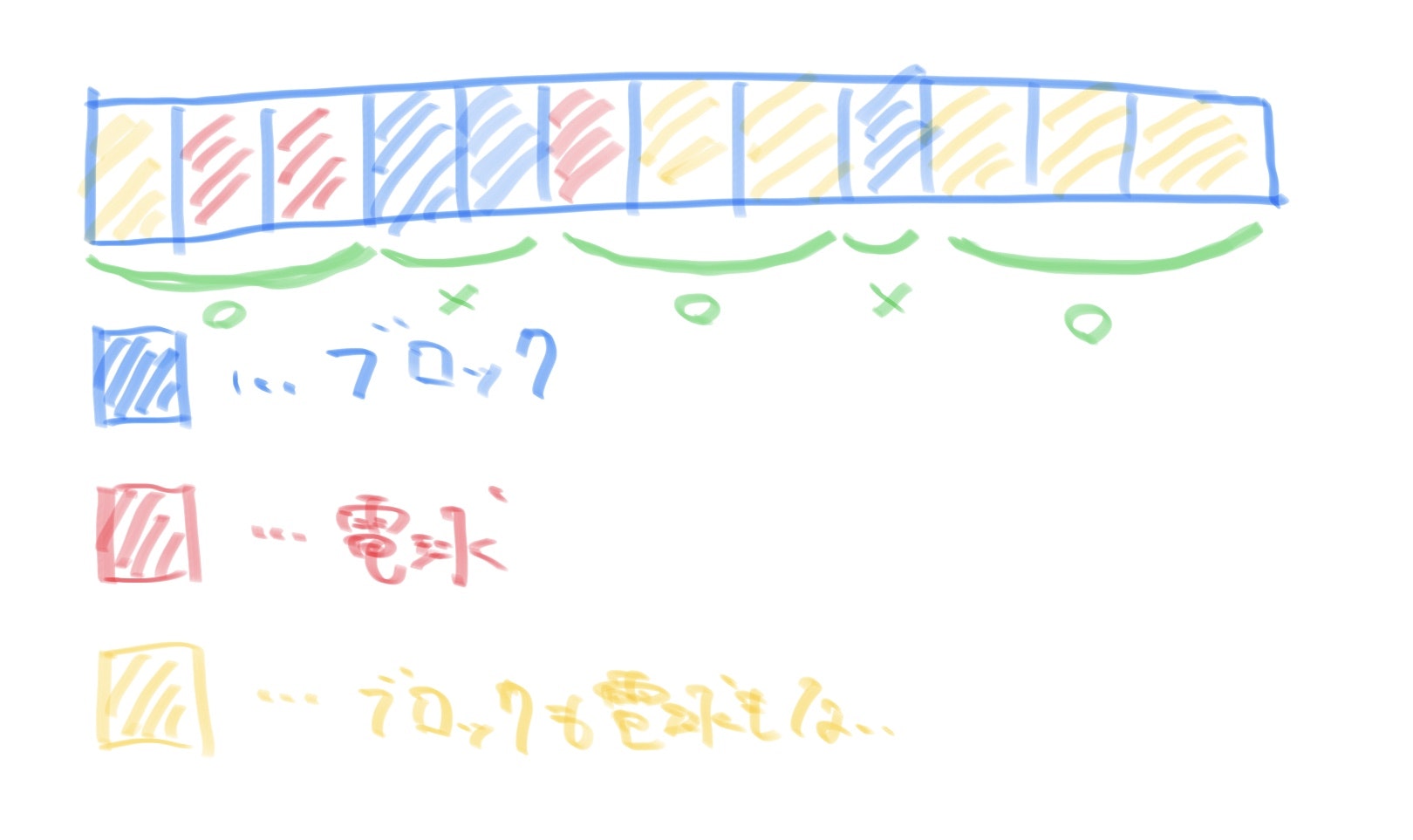
重要なのは、行方向と列方向をそれぞれ見た時にブロックの存在しない連続するマスでその連続するマスに一つでも電球が含まれる場合はそのマスに含まれる任意のマスが電球で照らされる、という点です。
言葉だけだとわかりにくいので図で示せば、以下のように◯の部分が照らされて×の部分が照らされません。ただし、行方向と列方向は別に考えていずれかの方向で照らされていればそのマスは照らされているとしてカウントすることができます。
つまり、ブロックのあるマスを0,電球のあるマスを1,それ以外のマスを-1として初期化すれば、groupby関数のkey引数にlambda x:x==0を指定することでグループに分けることができます。グループに分けることができれば先程の考察を実装に落とすのは難しくありません。また、行方向と列方向はインデックスを入れ替えるだけで簡単に実装することができます。
また、上記では概略しか説明していないので、実装がわからない場合は以下の提出を参考にしてください。
提出:https://atcoder.jp/contests/abc182/submissions/18669755
・その他の問題例
Codeforces #481(Div.3)B File Name
→ヒント:連続部分文字列の"xxx"の個数を求めたいので、xをキーとするグループを探した後にそれぞれのグループ内で"xxx"の個数を数えると実装が楽です。
→考察&提出:https://codeforces.com/contest/978/submission/100803274
HHKB2020E - Lamps
→ヒント:ABC182E Akariの類題です
→提出:https://atcoder.jp/contests/hhkb2020/submissions/18678355
ABC124D Handstand
→ヒント:直立と逆立ちの部分に分けた後にどの直立の部分を逆立ちにするのが効率良いか考えます。場合分けに注意してください。
→考察&提出:https://atcoder.jp/contests/abc124/submissions/18657446
ABC043D アンバランス
→ヒント:できるだけ短いアンバランスな文字列を考えるとランレングス圧縮が必要であることがわかります。場合分けに注意してください。
→考察&提出:https://atcoder.jp/contests/abc043/submissions/18664910
(2)変化する部分のみに着目する
・問題例1(ECR91A Three Indices)
重要なのは狭義極大値があるかの判定のみです。
ここで、1~nを並び替えたものは要素同士で異なるので、極大値が存在するときに必ず狭義です。従って、長さ$n$の配列に対して以下のコードで極大値を発見することができます。
g=[[key,len(list(group))] for key,group in groupby(range(n-1),key=lambda i:p[i+1]-p[i]>0)]
上記のコードにおけるグループの境目が極値になります。また、極大値はキーがTrue→Falseの順になる部分なので、このような部分が存在する場合は問題の条件に合わせて出力を行えば良いです。
→提出:https://codeforces.com/contest/1380/submission/100804735
・その他の問題例
ABC136D Gathering Children
→ヒント:十分な操作回数があるので最終的には連続2文字が"RL"となっている部分を往復します。従って、連続するRとLをそれぞれグループにまとめて人数を求めれば最終状態が求まります。図を書いて考えると良いです。
→考察&提出:https://atcoder.jp/contests/abc136/submissions/18665390
M-SOLUTIONS2020D Road to Millionaire
→ヒント:ECR91A Three Indicesの上位互換の類題です。極小値で買って極大値で売るのが最適ですが、初めの日に買うべきか最後の日に売るべきかを考える必要があります。また、コーナーケースを踏まないように注意してください。
→考察&提出:https://atcoder.jp/contests/m-solutions2020/submissions/18666219
(3)データサイズを圧縮する
操作が同じ繰り返し構造に対しまとめて操作を行える問題です。該当する問題を一つしか見つけられなかったので、有識者の方は教えていただけるとありがたいです。
・問題例1(ARC109C Large RPS Tournament)
愚直にシミュレーションを行うと間に合いませんが、繰り返している部分の勝つ手の並びは同じなのでまとめてシミュレートすれば良いです。また、繰り返している部分だけでなく余りの部分もあるので、[[繰り返しの部分,繰り返しの回数],余りの部分]としてシミュレートを行います。そして、シミュレートを行うには対戦する手がわかっている必要があるので、繰り返しの部分は偶数である必要があります。また、繰り返しの部分が偶数の時、シミュレートしている間は余りの部分も偶数なので同様にシミュレートを行えば良いです。
→考察&提出:https://atcoder.jp/contests/arc109/submissions/18666361