前回からの焼きまわしです
前回はこちら unityで物理エンジンを使わず当たり判定をした話 その①
本稿ではまだ範囲検索は書いてません。
あくまで、①の最適化です。
ビット演算を主にしたコアな内容に成ってます。
次に書く予定の②で範囲検索を模索します。
前回の記事との違い
前回、8ボクセルに分割したモートンオーダーを使った、空間分割について着目しました。
次回以降検索で負荷が掛る事が予想されます。
おさらいをしながら、今のうちに前回の記事の内容を最適化します
言葉
- 次元
- 通常次元はユークリッド空間における概念で語られます
- ゲームにおいても0次元(点)~3次元(xyz軸)等でデザインされます。
- 本稿においては、単に次元と指す場合はモートンオーダーにおける、階数を指す事とします。
- 2×2×2の立方が一つの単位(3次元)になります。
- 本稿ではプログラミングの効率化の為に更に3倍したものを単次元とします。
例)3次元(222)

例)6次元(444)
例)9次元(161616)
-
キー
単にキーと指す場合はモートンオーダーにおける3次元を一つの数値に変換した物(モーザー数列)とします。 -
モートンオーダー
長いのでzオーダーと言います。
物体が収まる最小次元の選定
一部前回の記事とかぶりますが、前回の部分も最適化も兼ねます。
- ある物体のサイズがおさまる次元数
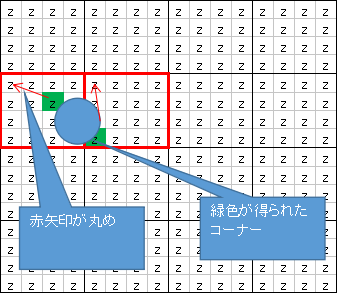
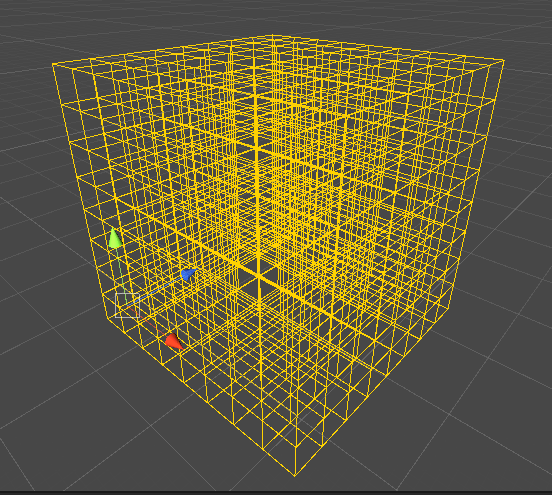
- 以下の黄色丸の半径は0.03です。紫の収まる次元を求めます。
-
半径を2倍した直径(0.06) を100倍して整数にします。端数は切り捨てます。この切り捨て行為が
グリッド化になります。 -
例)0.065468は6になり、0.69999も同様の6に丸められ同グリッドに収まると言う風に考えて下さい。
更に6は何の2の累乗範囲内に収まるか?と考えます。
2の累乗と言えば2進数ですね!
で、6は二進数で表すと0110です。
見た感じ、6の一桁上だと、必ず6が収まりそうですね
10進数でいうと、99は100に収まるのと同じ考えです。 -
一番左のビット(MSBと言います)が何番目かを求めます。
private int Msb32Bit(int v) {
if (v == 0) return -1;
v |= (v >> 1);
v |= (v >> 2);
v |= (v >> 4);
v |= (v >> 8);
v |= (v >> 16);
return Count32Bit(v) - 1;
}
private int Count32Bit(int v) {
var count = (v & 0x55555555) + ((v >> 1) & 0x55555555);
count = (count & 0x33333333) + ((count >> 2) & 0x33333333);
count = (count & 0x0f0f0f0f) + ((count >> 4) & 0x0f0f0f0f);
count = (count & 0x00ff00ff) + ((count >> 8) & 0x00ff00ff);
return (count & 0x0000ffff) + ((count >> 16) & 0x0000ffff);
}
- 6だと2(0番目から数えます)と言う数値が得られますね。更に+1します。
- これによって、9次元(本稿の便宜上3倍して9次元にしてます。)には収まりそうだ!と分かります。
- 9次元と言うとグリッドが888なので、0.08 * 0.08 * 0.08の範囲内に0.06直径の物体が収まって居る事が分かりますね!
private int GetLvFromSize(float hsize){
var norm = hsize * 2 * 100;
var msb = Msb32Bit((int)norm) + 1;
return msb * 3;
}
コーナーの算出
前回の記事だと、位置から8点それぞれ計算して割り出していました。
ですが、これは無駄で、位置とサイズで、どのボクセルが必要か求まります。
- 位置とサイズから、左上の角と右下の角の2点コーナーポイントを算出します。
private void Get3DCorner(float3 xyz,float hsize,out ulong start ,out ulong end){
xyz += 10000;//座標にマイナスが発生しないようオフセット+10000
var negative = (xyz - hsize) * 100;//offset 最小ボクセル0.01の正規化
var positive = (xyz + hsize) * 100;//offset 最小ボクセル0.01の正規化
start = BitSeparateFor3D((ulong)negative.x) | BitSeparateFor3D((ulong)negative.y)<<1 | BitSeparateFor3D((ulong)negative.z)<<2;
end = BitSeparateFor3D((ulong)positive.x) | BitSeparateFor3D((ulong)positive.y)<<1 | BitSeparateFor3D((ulong)positive.z)<<2;
}
private ulong BitSeparateFor3D(ulong n )
{
var s = n;
s = ( s | s<<32 ) & 0xffff00000000ffff;
s = ( s | s<<16 ) & 0x00ff0000ff0000ff;
s = ( s | s<<8 ) & 0xf00f00f00f00f00f;
s = ( s | s<<4 ) & 0x30c30c30c30c30c3;
s = ( s | s<<2 ) & 0x9249249249249249;
return s;
}
次元の端数
ここから更に少し難しくなります。
-
単次元は2×2×2です。
前述の通り2D、3Dの世界とは違って、zオーダーで言うところの単次元は0~1×0~1×0~1の8つの立方体で構成されています。
さらにキー変換するとzyx一組、3ビットで表現されます。
zyxで一組と言うと、xが欠けたzyだけ(2ビット)の世界はどうなるのか?と言うことを考えます。 -
yxが欠けたZだけの世界はどうなのかと言うと、こうなります。
-
これを次元の端数とみなすと、例えば101があったとして、こう言えます。
1は0.1次元、10は0.2次元、101は0.3次元=1次元
こう見ると、端数を三つづつなので、端数を整数で扱いやすいよう予め3の倍数しておきます。 -
具体的には
1が1次元で10は2次元で101は3次元となります。
こうして、1ビット分が1次元に成りました!
3ビット一組3次元で2×2×2の単次元が出来るみたいなイメージですね。
端数次元を踏まえどのボクセルに収まるかを算出
前述したコーナーポイントから、物体が収まる次元数(図の赤枠の大きさ)を求め、そこから更に2点間が入る最適な次元を求めます。
イメージとしてはこんな感じです
//lvが次元
//start,endがコーナーポイント
//丸め
var lvstart = start >> lv;
var lvend = end >> lv;
//次元の端数算出
var fraction = GetFractionCount(lvstart,lvend);
lv += fraction;
- 端数次元算出処理です。
赤枠一つで収まるのか、2個必要なのかをXYZ軸で調べて、端数の次元数とします。
不格好ですが、場合分けの方がスッキリします。
private int GetFractionCount(ulong start ,ulong end){
var shift = 0;
if (!(start & 0x1).Equals(0) || (end & 0x1).Equals(0)) return shift;
shift++;
if (!(start & 0x2).Equals(0) || (end & 0x2).Equals(0)) return shift;
shift++;
if (!(start & 0x4).Equals(0) || (end & 0x4).Equals(0)) return shift;
shift++;
return shift;
}
-
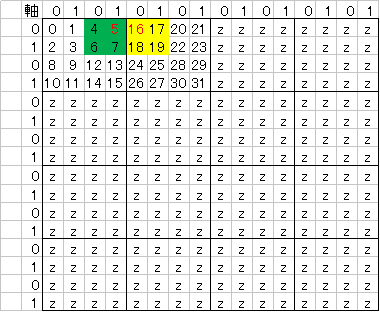
キーが図のように1~31まであったとします。
(簡単の為2Dで説明)
数値が順にZ字を書くようにうねっています。
軸だけ見るとxbit、ybitは全て01の交互である事が分かります。
この時にレベル2で見た時に(図は2D図なので2次元づつ上がってます。)2×2マスになります。 -
例えば赤字の5と16をみて下さい。レベル2で見ると緑と黄いろのマスが浮かびます。
05は00 01 01です
16は01 00 00です
太字を見てください。太字箇所がレベル2です。
この時に太字箇所の1ビット目が05と16だと1→0と逆転の関係にある事が分かります。
この事は一つのグリッドで表現出来ないグリッドの分割が発生する軸と言うことを意味します。
以降グリッド跨ぎと言います。
-
例えば
17は01 00 01
20は01 01 00
で太字1ビット目が0→1の関係なので跨いでいないと言うことに成ります。 -
ここまでの説明をすると
跨いでいない状態をXYZ軸で順次チェックして、端数の次元数がカウントされます。
そして最後に端数を次元に足しこめば、元々立方体だったコーナーにおける最小グリッドが、少数次元まで落ちた形(横長だったり板状だったりします。)で算出されます。
この外形を使ってコーナーに配置していきます。
コーナーへの配置
- 端数次元によって、最小グリッドの次元が分かりました。
- スタート地点と終了地点が分かってます。
- 他の点がまだ分かって居ません。
- 分割数と方向が分かれば配置場所が分かります
分割数と分割する軸を求めます。
//lvstartは元の立方体で丸められた左上コーナー。lvendは右下
var dim = (byte)(Truncate(lvstart ^ lvend,fraction) & 0x7);//差分体積の共有空間の端数次元3ビットのみを抽出
start = Truncate(start, lv);
end = Truncate(end, lv);
private ulong Truncate(ulong v,int lv,uint offset = 0){
return ((v >> lv ) + offset) << lv;
}
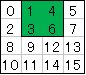
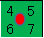
下図の場合、赤丸の左上コーナーは4で右下コーナーは7になります。
(簡単の為2Dで説明)
-
分割数算出
4は0100
7は0111
XORを取ると差分が出て
0011になります。
又、前述の関数を使うと端数が2次元になります。
truncate関数は次元以降を切り捨てる関数になります。
0011を2次元分切り捨てると0になります。
これの意味するところは、X方向に0(一個分)Y方向に0(一個分)必要となります。 -
もう一つやってみます。
4は0100
6は0110
xorは0010
今回の端数次元は0になります。
切り捨てが発生しないので、0010となります。
これの意味するところは、X方向に0(一個分)Y方向に1(2個分)必要となります。
このように計算によって縦横の必要数が分かります。
後は、配置していきます。
start = Truncate(start, lv);
end = Truncate(end, lv);
var oct = new OctreeVoxel();
switch (dim){
case 0:{//1box内
oct.len = 1;
oct.v[0] =start;//0
break;}
case 1:{//左右2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//1
break;
}
case 2:{//上下2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//2
break;
}
case 3:{//前面x,y 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,1, 2, start, end);
oct.v[3] = end;//7
break;
}
case 4:{//前後2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//4
break;
}
case 5:{//上面 x,z 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,1, 4, start, end);
oct.v[3] = end;//5
break;
}
case 6:{//側面 y,z 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,2, 4, start, end);
oct.v[3] = end;//6
break;
}
case 7:{//8boxel
oct.len = 8;
oct.v[0] = start;//0
Octree8Box(&oct,start, end);
oct.v[7] = end;//7
break;
}
}
コーナーへの登録をします
最初のtruncate処理の所で始端と終端を端数付きの次元でそれぞれ丸めます。
dimには得られた縦横配置場所が入っています。ビットで表現され、最大7(111)です。zyxが何個要るか?が分かって居ます。0なら1個、1なら2個です。
Z字を書くように象限分けをすると、何番に配置するか分かります。
例えばdimが6だったらビットで表現すると110となり、前後2×縦2×横1の配置になり
下図で言うと0246の象限への配置が必要と分かります。

- ケースで場合分けしているのは、後の処理を勘案するとソーティングされていた方が効率的なのでこの時点で既にソーティングしてしまいます。
この時に最小のソーティングで済ませる為に、場合分けで済ませます。 - ex)下図の例だと、1→4→3→6となってしまう。
こういうパターンもある為
(簡単の為2Dで説明)
値は最大で8点を格納できる構造体を用意して格納します。
[Serializable]
public unsafe struct OctreeVoxel{
public byte len;
public fixed ulong v[8];
}
- 2boxの場合はstartとendだけの登録で終わりです。
それ以上の分割数
-
4box
OctreeCompositに与える1番目の引数は象限を与えます。
それに応じたビット数をstartとendのビット数を抽出し交互に合成することで、象限のキーが得られます。
startとendは決まっているので、間の2象限の値を比較して少ない順に入れ替えます。 -
8boxの方もやって居る事は一緒ですが、ソートの入れ替えが少ない回数で行っています。
private unsafe void Octree4Box(OctreeVoxel* oct, byte l,byte r,ulong start,ulong end){
oct->v[1] = OctreeComposit(l, start, end);
oct->v[2] = OctreeComposit(r, start, end);
CompareSwap(ref oct->v[1],ref oct->v[2]);
}
private unsafe void Octree8Box(OctreeVoxel* oct,ulong start, ulong end){
oct->v[1] = OctreeComposit(1, start, end);
oct->v[2] = OctreeComposit(2, start, end);
oct->v[3] = OctreeComposit(3, start, end);
oct->v[4] = OctreeComposit(4, start, end);
oct->v[5] = OctreeComposit(5, start, end);
oct->v[6] = OctreeComposit(6, start, end);
CompareSwap(ref oct->v[2], ref oct->v[3]);
CompareSwap(ref oct->v[4], ref oct->v[5]);
CompareSwap(ref oct->v[1], ref oct->v[3]);
CompareSwap(ref oct->v[4], ref oct->v[6]);
CompareSwap(ref oct->v[1], ref oct->v[2]);
CompareSwap(ref oct->v[5], ref oct->v[6]);
CompareSwap(ref oct->v[1], ref oct->v[5]);
CompareSwap(ref oct->v[2], ref oct->v[6]);
CompareSwap(ref oct->v[2], ref oct->v[4]);
CompareSwap(ref oct->v[3], ref oct->v[5]);
CompareSwap(ref oct->v[1], ref oct->v[2]);
CompareSwap(ref oct->v[3], ref oct->v[4]);
CompareSwap(ref oct->v[5], ref oct->v[6]);
}
private ulong OctreeComposit(byte pos,ulong start,ulong end){
switch (pos){
case 0:{return start;}
case 1:{return ((start & 0x6db6db6db6db6db6) | (end & 0x9249249249249249));}
case 2:{return ((start & 0xdb6db6db6db6db6d) | (end & 0x2492492492492492));}
case 3:{return ((start & 0x4924924924924924) | (end & 0x66db6db6db6db6db));}
case 4:{return ((start & 0x66db6db6db6db6db) | (end & 0x4924924924924924));}
case 5:{return ((start & 0x2492492492492492) | (end & 0xdb6db6db6db6db6d));}
case 6:{return ((start & 0x9249249249249249) | (end & 0x6db6db6db6db6db6));}
default:{return end;}
}
}
private void CompareSwap(ref ulong x,ref ulong y){
if (x.Equals(y)){return;}
if (x <= y) return;
x ^= y;
y ^= x;
x ^= y;
}
ここから先は範囲検索が出来ないと無理なので
- ここまでで、おさらいが入った最適化をしています。
bit演算とzオーダーの親和性の高さから前回に比べビット演算を多用してます。
今までと概念ががらっと変わったように見えますが、欲しい結果は前回と同じです。
OctreeVoxelの中身が取得できれば検索範囲だろうが、オブジェクトが持つAABBだろうが、位置とサイズさえあれば、いきなり範囲ボクセルを取得できるようになります。
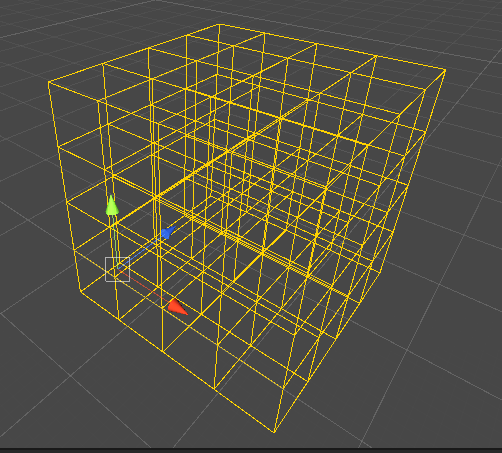
試してみたかったら、下のスクリプトを作成して適当なオブジェクトにMortonTestをアタッチしてもらえれば確認できます。
サイズに値を入れて、オブジェクトをぐりぐり動かしてみてください。
最適化されたグリッドが表示されます。
ここから先AABBと範囲の衝突可能性になりますが
ざっくり言うと、分割したボクセルを全て並べて範囲検索すれば良いだけの話なのですが
次が範囲検索と言うことで、複雑な問い合わせが予想されます。
そもそもがパフォーマンス向上が目的なので、ここできっちり最適化を行いました。
次はいつになるか分かりませんが、今度コソ②へ!
MortonTest.cs
using System;
using Unity.Mathematics;
using UnityEngine;
public unsafe class MortonTest : MonoBehaviour
{
[SerializeField]
private float size;
[SerializeField]
private int maxlv;
[SerializeField]
private ulong[] mlist;
[Serializable]
public unsafe struct OctreeVoxel{
public byte len;
public fixed ulong v[8];
}
void OnDrawGizmos()
{
// Draw a yellow sphere at the transform's position
var lscale = (float3) (this.transform.localScale);
var scale = lscale.x > lscale.y ?
lscale.x > lscale.z ? lscale.x : lscale.z :
lscale.y > lscale.z ? lscale.y : lscale.z;
var pos = (float3) this.transform.position ;
var csize = scale * size;
Gizmos.color = Color.yellow;
Gizmos.DrawWireSphere(pos,csize);
Gizmos.color = Color.magenta;
var ml = GetOctree(pos, csize,out maxlv);
mlist = new ulong[8];
for (var i = 0; i < mlist.Length; i++){
var mli = ml.v[i];
if (!mli.Equals(0)){
var start = Truncate(mli, (int)maxlv);
var outpos1 = GetPosFromMorton(start);
var end = Truncate(mli , (int)maxlv,1);
var outpos2 = GetPosFromMorton(end - 1);
var dsize = (outpos2 - outpos1);
Gizmos.DrawWireCube(outpos1 + (dsize * 0.5f), dsize);
}
mlist[i] = ml.v[i];
}
}
private float3 GetPosFromMorton(ulong aa)
{
var tmp = float3.zero;
for (var i = 0; i < 64; i++){
var d = (i + 1) % 3;
if (!(aa & 0x01).Equals(0)){
var div = (int) (i / 3);
switch (d){
case 1:{tmp.x += (1 << div);break;}
case 2:{tmp.y += (1 << div);break;}
default:{tmp.z += (1 << div);break;}
}
}
aa >>= 1;
}
tmp /= 100;
tmp -= 10000;
return tmp;
}
private int GetLvFromSize(float hsize){
var norm = hsize * 200;
var msb = Msb32Bit((int)norm) + 1;
return msb * 3;
}
private int Msb32Bit(int v) {
if (v == 0) return -1;
v |= (v >> 1);
v |= (v >> 2);
v |= (v >> 4);
v |= (v >> 8);
v |= (v >> 16);
return Count32Bit(v) - 1;
}
private int Count32Bit(int v) {
var count = (v & 0x55555555) + ((v >> 1) & 0x55555555);
count = (count & 0x33333333) + ((count >> 2) & 0x33333333);
count = (count & 0x0f0f0f0f) + ((count >> 4) & 0x0f0f0f0f);
count = (count & 0x00ff00ff) + ((count >> 8) & 0x00ff00ff);
return (count & 0x0000ffff) + ((count >> 16) & 0x0000ffff);
}
private void Get3DCorner(float3 xyz,float hsize,out ulong start ,out ulong end){
xyz += 10000;//座標にマイナスが発生しないようオフセット+10000
var negative = (xyz - hsize) * 100;//offset 最小ボクセル0.01の正規化
var positive = (xyz + hsize) * 100;//offset 最小ボクセル0.01の正規化
start = BitSeparateFor3D((ulong)negative.x) | BitSeparateFor3D((ulong)negative.y)<<1 | BitSeparateFor3D((ulong)negative.z)<<2;
end = BitSeparateFor3D((ulong)positive.x) | BitSeparateFor3D((ulong)positive.y)<<1 | BitSeparateFor3D((ulong)positive.z)<<2;
}
private ulong BitSeparateFor3D(ulong n )
{
var s = n;
s = ( s | s<<32 ) & 0xffff00000000ffff;
s = ( s | s<<16 ) & 0x00ff0000ff0000ff;
s = ( s | s<<8 ) & 0xf00f00f00f00f00f;
s = ( s | s<<4 ) & 0x30c30c30c30c30c3;
s = ( s | s<<2 ) & 0x9249249249249249;
return s;
}
private int GetFractionCount(ulong start ,ulong end){
var shift = 0;
if (!(start & 0x1).Equals(0) || (end & 0x1).Equals(0)) return shift;
shift++;
if (!(start & 0x2).Equals(0) || (end & 0x2).Equals(0)) return shift;
shift++;
if (!(start & 0x4).Equals(0) || (end & 0x4).Equals(0)) return shift;
shift++;
return shift;
}
private ulong Truncate(ulong v,int lv,uint offset = 0){
return ((v >> lv ) + offset) << lv;
}
private OctreeVoxel GetOctree(float3 pos,float hSize,out int lv){
lv = GetLvFromSize(hSize);
Get3DCorner(pos,hSize,out var start, out var end);
var lvstart = start >> lv;
var lvend = end >> lv;
var fraction = GetFractionCount(lvstart,lvend);//次元の端数
lv += fraction;
var dim = (byte)(Truncate(lvstart ^ lvend,fraction) & 0x7);//差分体積の共有空間の端数次元3ビットのみを抽出
start = Truncate(start, lv);
end = Truncate(end, lv);
var oct = new OctreeVoxel();
switch (dim){
case 0:{//1box内
oct.len = 1;
oct.v[0] =start;//0
break;}
case 1:{//左右2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//1
break;
}
case 2:{//上下2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//2
break;
}
case 3:{//前面x,y 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,1, 2, start, end);
oct.v[3] = end;//7
break;
}
case 4:{//前後2box
oct.len = 2;
oct.v[0] = start;//0
oct.v[1] = end;//4
break;
}
case 5:{//上面 x,z 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,1, 4, start, end);
oct.v[3] = end;//5
break;
}
case 6:{//側面 y,z 4box
oct.len = 4;
oct.v[0] = start;//0
Octree4Box(&oct,2, 4, start, end);
oct.v[3] = end;//6
break;
}
case 7:{//8boxel
oct.len = 8;
oct.v[0] = start;//0
Octree8Box(&oct,start, end);
oct.v[7] = end;//7
break;
}
}
return oct;
}
private void Octree4Box(OctreeVoxel* oct, byte l,byte r,ulong start,ulong end){
oct->v[1] = OctreeComposit(l, start, end);
oct->v[2] = OctreeComposit(r, start, end);
CompareSwap(ref oct->v[1],ref oct->v[2]);
}
private void Octree8Box(OctreeVoxel* oct,ulong start, ulong end){
oct->v[1] = OctreeComposit(1, start, end);
oct->v[2] = OctreeComposit(2, start, end);
oct->v[3] = OctreeComposit(3, start, end);
oct->v[4] = OctreeComposit(4, start, end);
oct->v[5] = OctreeComposit(5, start, end);
oct->v[6] = OctreeComposit(6, start, end);
CompareSwap(ref oct->v[2], ref oct->v[3]);
CompareSwap(ref oct->v[4], ref oct->v[5]);
CompareSwap(ref oct->v[1], ref oct->v[3]);
CompareSwap(ref oct->v[4], ref oct->v[6]);
CompareSwap(ref oct->v[1], ref oct->v[2]);
CompareSwap(ref oct->v[5], ref oct->v[6]);
CompareSwap(ref oct->v[1], ref oct->v[5]);
CompareSwap(ref oct->v[2], ref oct->v[6]);
CompareSwap(ref oct->v[2], ref oct->v[4]);
CompareSwap(ref oct->v[3], ref oct->v[5]);
CompareSwap(ref oct->v[1], ref oct->v[2]);
CompareSwap(ref oct->v[3], ref oct->v[4]);
CompareSwap(ref oct->v[5], ref oct->v[6]);
}
private ulong OctreeComposit(byte pos,ulong start,ulong end){
switch (pos){
case 0:{return start;}
case 1:{return ((start & 0x6db6db6db6db6db6) | (end & 0x9249249249249249));}
case 2:{return ((start & 0xdb6db6db6db6db6d) | (end & 0x2492492492492492));}
case 3:{return ((start & 0x4924924924924924) | (end & 0x66db6db6db6db6db));}
case 4:{return ((start & 0x66db6db6db6db6db) | (end & 0x4924924924924924));}
case 5:{return ((start & 0x2492492492492492) | (end & 0xdb6db6db6db6db6d));}
case 6:{return ((start & 0x9249249249249249) | (end & 0x6db6db6db6db6db6));}
default:{return end;}
}
}
private void CompareSwap(ref ulong x,ref ulong y){
if (x.Equals(y)){return;}
if (x <= y) return;
x ^= y;
y ^= x;
x ^= y;
}
}
```
</div></details>