この記事での焦点
弾幕シューティングや物量が多いゲームや、衝突対象のオブジェクトが密集しがちな演算において、パフォーマンス劣化を回避できないか模索してみました。
unityでは当たり判定は物理エンジンを介して行われます。
一概に当たり判定と言ってもoncolliderやontrigger、Raycast等があります。
今回の記事では、応力や概形は従来のコライダーを利用します。完全に物理エンジンを作るわけではありません。
又、raycastも割とステートフルで帰って来ますし、又job化も容易なのでこれも対象にしません。
今回の記事では単純にontriggerの部分を削れないか?と言う話をします。
しかも物理エンジンのような様々な概形を考慮せず、球形の2点間の境界衝突に限って考察してみます。
まず使ってみようと思った手法
点間の衝突においては、ざっくりとした衝突、その後で精細な衝突を考えます。
まずざっくりとした衝突を考えてみます。
空間分割
空間をはじめから固定のグリッドで区切ります。
どこのマスに居るのか?と問い合わせるだけで、マスの中身を引っ張ります。
キーはマスの座標を丸めた物になります。
グリッド分割
良く使われるのはGrid分割
一度全座標データをグリッドに区切って用意します。
後は衝突問い合わせの都度、座標データを参照します。
データが共有のメモリに集まっている前提
//このような感じのデータが集まってると仮定します
var Players = new List<Transform>();
毎フレーム登録
//以下の感じでpositionの整数を切り捨てたデータを毎フレーム登録します。
var a =new NativeMultiHashMap<int2, int>(Players.Count ,Allocator.TempJob);
for (var i = 0; i < Players.Count; i++) {
var t = Players[i];
a.Add(new int2((int)t.position.x,(int)t.position.y), i);
}
需要があったら問合せ
//座標グリッド(整数)指定で範囲問合せ
a.TryGetFirstValue(問い合わせたい座標, out var item, out var iterator);
while (a.TryGetNextValue(out item,ref iterator))
{
//座標グリッドに当てはまる対象を精査
}
※nativearrayを使ってますが、dictionaryでも表現できます。
キーのポジションのグリッド内に複数データがある事を意識してください。
int3のX,yが座標、Zにiを入れてキーが唯一であることを保証すれば可能です
この手法の気に成るところ
・グリッドが固定でオブジェクト自体が大きさを持つ場合AABBの検索が出来ない。
もっと言うとAABB分全てのマスに対して捜査しなければ成らない。
・キーとデータの登録が結構重い。毎フレームだと地味に効いてくる重さ
と言うことで、雑フェーズでの篩としては粗いです。
又、ダイナミックアクセスが主役で、グリッド跨ぎの範囲検索が絶望的になります。
結論としてこの手法は採用没にしました。
更なる手法の模索への旅に
モートンオーダーによるOctreeの検討
これは一つの記事が書けてしまいますので、こちらを
[http://marupeke296.com/COL_2D_No8_QuadTree.html]
[http://marupeke296.com/COL_3D_No15_Octree.html]
モートンオーダーの概要
記事の概略を説明します。
モートンオーダーは簡単に言うと、2次元(3次元も)の座標をグリッド毎に分割するのは同じです。
ですが、キーに特徴があって2次元(3次元)の座標を一筆書きで1次元で表現します。
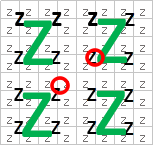
又、見た目「Z」の形で一筆書きをすることにより特殊な計算が可能になります。
あるグリッドに着目したとして、AABBを定義すると、最大最小の2点を与えて計算式に当てはめるとグリッドの最大最小のインデックスを割り出すことが可能です。
(正確に言うと、2点間が収まる範囲までグリッドを拡張します。)
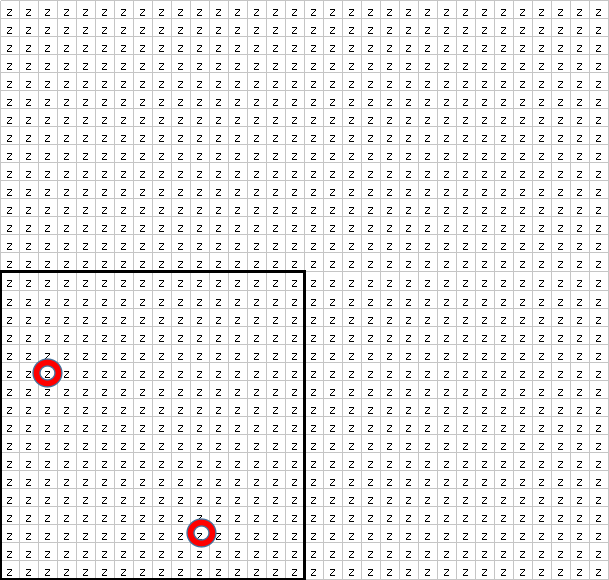
こんなイメージで赤丸2点を計算式に入れると、見るべきグリッドが、いきなり持ち上がります
これによってグリッド跨ぎと言う概念を無くします。
又空間分の専用の木を作ります。
この手法の気に成るところ
・専用の木を作ってます。毎フレーム動く物が前提のゲームエンジンだと(キーと精製等がいくら早いとはいえ)パフォーマンスをかえって劣化させかねません。
・グリッドが跨げる(グリッド自体が変わる)と言いましたが万能ではありません。
同所属空間(グリッドのレベルみたいな感じ)で同Z内におさまる態になるまで、強制的に拡張されます。
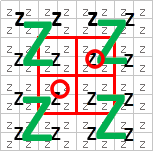
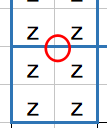
下の図を見てみてください。
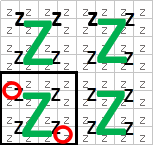
よく見るパターンですね
赤丸2点間が罫線(緑のZ)まで所属空間グリッドが拡張されます。
これは想定の範囲内で、そもそも初段の範囲検索としてはかなりいい線で範囲限定が出来てると思います。
つまり、何が何でも一つのグリッド(Z)で解決しようとします。
言い換えると、場所によってZが肥大化し、場所によっては全件検索になります。
もっと言い換えると、場所によってパフォーマンスが劣化する羽目に・・・
ここから更なる手法を模索してみます。
その①
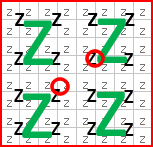
あるオブジェクトが大きさを持っていたとして、その大きさが収まる所属空間のグリッドで、それ以上大きさ拡張をせずに矩形の角のポイントで範囲検索をしたらどうか?
と言うところに着目します。
赤丸2点が収まるグリッド幅は2×2ですが、青グリッド4つを検索するイメージです
今回の記事ではココを書きます。
その②
なるべくなら木を作りたく有りません。
如何に高速とは言え、もうDBと言って良いような構造化は避けます。
毎フレーム作成しても大丈夫なようにします。
幾ら所属空間を変えられるとは言え、元のキーは線形(一次元)のキーである事と、それが一つながりの線状で空間を表現しているところに着目します。
モートンオーダーのある範囲を指定すると、立方体の範囲を指定出来る事に着目し
オブジェクトの座標をモートンオーダーに変更し、配列化し、範囲探索できるところを目指します。
これは次回書きます
実装
Get3DMortonOrderに座標を与えるとモートンオーダーで利用できる3ビット間隔の3Dキーが取得できます。
private ulong Get3DMortonOrder(float3 xyz)
{
xyz += 10000; //座標にマイナスが発生しないようオフセット+10000
xyz *= 100;//offset 最小ボクセル0.01の正規化
return BitSeparateFor3D((ulong)xyz.x) | BitSeparateFor3D((ulong)xyz.y)<<1 | BitSeparateFor3D((ulong)xyz.z)<<2;
}
private ulong BitSeparateFor3D(ulong n )
{
var s = n;
s = ( s | s<<32 ) & 0xffff00000000ffff;
s = ( s | s<<16 ) & 0x00ff0000ff0000ff;
s = ( s | s<<8 ) & 0xf00f00f00f00f00f;
s = ( s | s<<4 ) & 0x30c30c30c30c30c3;
s = ( s | s<<2 ) & 0x9249249249249249;
return s;
}
これを使ってフレームの最初にキーの配列を作ります。
var morton = new List<ulong>();
for (var i = 0; i < Players.Count; i++){
morton.Add(Get3DMortonOrder((float3)Players[i].position));
}
そして、それを範囲探索できるようにします。
※範囲探索や探索については本稿では書きません。グリッド選定まで書きます。
GetLvFromSizeである大きさを持ったオブジェクトの階乗範囲内に収まるようなグリッドの所属空間レベルを求めます。
private static int GetLvFromSize(float size){
var normal = size * 100;//offset 最小ボクセル0.01の正規化
var msb = Msb32Bit((int)normal) + 1;
return (int)msb;
}
private int Count32Bit(int v) {
var count = (v & 0x55555555) + ((v >> 1) & 0x55555555);
count = (count & 0x33333333) + ((count >> 2) & 0x33333333);
count = (count & 0x0f0f0f0f) + ((count >> 4) & 0x0f0f0f0f);
count = (count & 0x00ff00ff) + ((count >> 8) & 0x00ff00ff);
return (count & 0x0000ffff) + ((count >> 16) & 0x0000ffff);
}
private int Msb32Bit(int v) {
if (v == 0) return -1;
v |= (v >> 1);
v |= (v >> 2);
v |= (v >> 4);
v |= (v >> 8);
v |= (v >> 16);
return Count32Bit(v) - 1;
}
やってることは検索範囲の一辺大きさグリッド大きさを求めます。この大きさは2の乗数でレベルとします。
又今回は1単位を0.01とします。1だと検索ボクセルが大きすぎたので・・・
(例、レベル5なら一辺0.32の立方体、レベル6なら0.64の立方体が単位になります。)
このレベル固定で(モートンオーダーの機能の自動拡張を使わず)検索したいポイント周辺を検索します。
この8ポイントそれぞれでAABBサイズのグリッドを求めます。
public void GetOctreeList(List<ulong> aalist,List<ulong> bblist,float3 pos,float hsize){
var lv = GetLvFromSize(hsize);
var bpbb = (ulong)0;
var rid = 0;
for (var j = 0; j < 8; j++){
GetAaBbZOrder(pos, hsize, j, lv, out var aa, out var bb);
var idx = aalist.IndexOf(aa);
if (idx < 0){
if (!aa.Equals(bpbb)){
aalist.Add(aa);
bblist.Add(bb);
rid = aalist.Count - 1;
}
else{
bblist[rid] = bb;
}
}
bpbb = bb;
}
}
private int GetAaBbZOrder(float3 pos,float hSize,int id,int lv,out ulong aa,out ulong bb){
var opos = Get8ZPoint(pos,hSize,id);
var ltd = Get3DMortonOrder(opos);
var gLv = lv * 3;
var voxel = ltd >> gLv;
aa = (voxel << gLv);
bb = ((voxel + 1) << gLv) ;
return gLv;
}
private static float3 Get8ZPoint(float3 pos,float hSize ,int zid){
switch (zid){
case 0:{return new float3(pos.x - hSize,pos.y - hSize,pos.z - hSize);}
case 1:{return new float3(pos.x + hSize,pos.y - hSize,pos.z - hSize);}
case 2:{return new float3(pos.x - hSize,pos.y + hSize,pos.z - hSize);}
case 3:{return new float3(pos.x + hSize,pos.y + hSize,pos.z - hSize);}
case 4:{return new float3(pos.x - hSize,pos.y - hSize,pos.z + hSize);}
case 5:{return new float3(pos.x + hSize,pos.y - hSize,pos.z + hSize);}
case 6:{return new float3(pos.x - hSize,pos.y + hSize,pos.z + hSize);}
case 7:{return new float3(pos.x + hSize,pos.y + hSize,pos.z + hSize);}
}
return float3.zero;
}
少しづつ解説します。
GetOctreeListに探索する中点を与えます。
その探索サイズからレベルを取得します。
GetAaBbZOrderで矩形の頂点8ポイントで、レベル固定のグリッドを取得します。
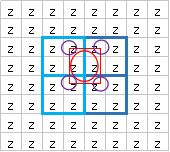
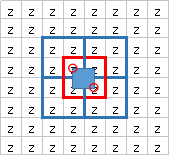
例えば赤丸の位置があったとします。
紫丸の隅のポイントの座標をそれぞれモートンオーダーのキー化します。
そのキーの(レベル×3)以降のビットを0にします。
これによりそれぞれの青四角の左上位置のキーを取得できます。
そのキーの(レベル×3⁺1)以降のビットを0にします。
これによりそれぞれの青四角の右下位置のキーを取得できます。
8点で順番に行い、繰り替えしますが、z順で連続するかどうかは決まっていますので、前回の最大値と今回の最小値比較するだけの簡単比較で、重複排除が可能です。
これにより、モートンオーダーでの連続した空間の最小分割が可能になります。
最終的に最大8件のaaとbbの範囲のリストが得られます。
このリストで得られたモートンオーダーの座標を可視化したものがこのような感じになります。
普通のモートンオーダーに比べて範囲検索の数は増えますが、範囲がはるかに少ない事が分かります。
縦は収まっているが横がまたがっている
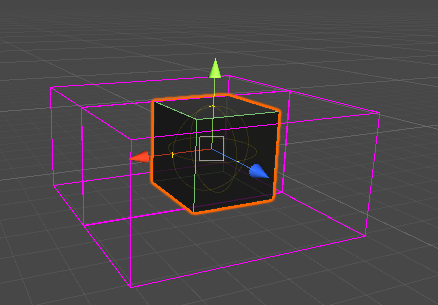
が、左右は一続きの為、連続して一回の検索で済む
ただ前後は分割されている
8ボックス分割されるパターン
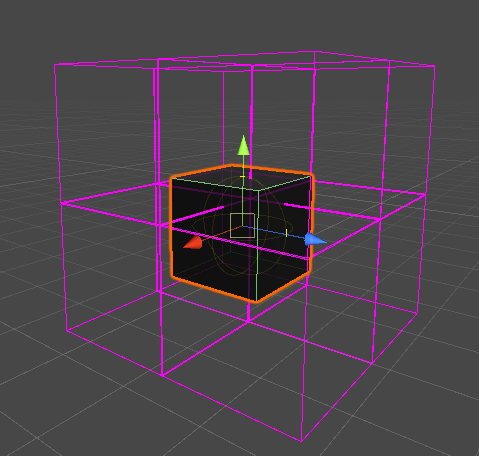
空間によってはまたいでしまう。8回検索が必要
4ボックスに収まるパターン

このように上下グリッドに分かれているが左右は連続しているため分割しないで済んでいる(左右は一回の範囲検索で済む)
2ボックスに収まるパターン
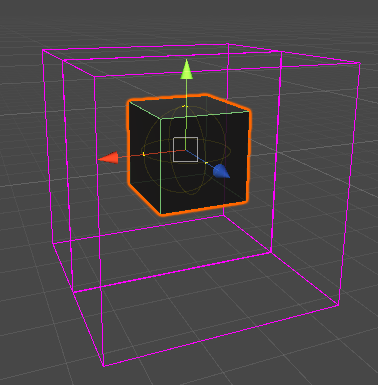
前後のZで連続していないが前のz後ろのz一回の検索で済む
8ボックスにまたがっているが1ボックスに収まるパターン
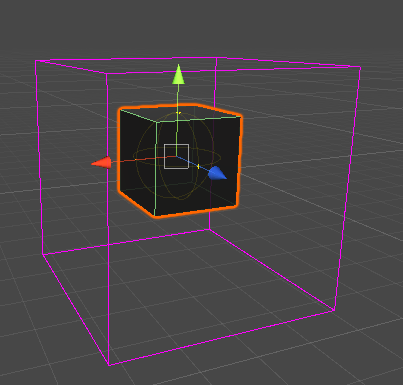
8ボックスにまたがっているにも関わらず、一続きの空間で8ボックス分が全て一回の範囲検索で済む
これにより、いきなり検索対象のグリッドを最大8グリッドまでに絞り込む事ができ、探索すべきのリストを得る事ができました。。
後は得られたグリッドの範囲内のオブジェクトの距離を精査すれば良い訳です。
次回は範囲検索について書きます。