多変量統計的プロセス管理（MSPC）をRで実装してみた

• 製造業出身のデータサイエンティストがお送りする記事
• 今回は製造業で使える異常検知手法を実装し整理しました。

はじめに

先日、ご紹介した異常検知（MSPC）をRでも実装したのでご紹介します。
MSPCとは何か？と言うことについては前の記事に書いておりますので、そちらをご参照ください。

Rの実装

# 必要なライブラリーのインポート
rm(list=ls())
library(data.table)
library(ggplot2)
library(scales)
library(dplyr)
library(foreach)
library(doParallel)

# 学習データの読込み
x_tra <- fread("../data/train_data.csv")
col_tra <- ncol(x_tra)                       #変数の数
row_tra <- nrow(x_tra)                       #データ数
date_tra <- x_tra %>% select(1:2)
x_tra <- x_tra %>% select(3:col_tra)
col_tra <- ncol(x_tra)                       #変数の数を再度計算
x_tra_std <- scale(x_tra,apply(x_tra,2,mean),apply(x_tra,2,sd))   #標準化

# prcompを使った主成分分析
# prcompの逆行列はムーアペンローズの一般化逆行列を使用
# prcompでは固有値ではなく、標準偏差が自動計算される
x_tra_pca <- prcomp(x_tra_std, scale=F)      #データの共分散行列を固有値分解
x_tra_pca_center <- x_tra_pca$center
EV_tra <- x_tra_pca$sdev^2                   #固有値(標準偏差の2乗)
score_tra <- x_tra_pca$x                     #主成分得点
vector_tra <- x_tra_pca$rotation             #固有ベクトル(学習データ)

今回は固有値の選択方法を前回の累積寄与率で算出せずに固有値が1以上を主要な主成分とし、その他をQ統計量としました。
固有値の意味合いを考えた際に固有値が1以上ということは元の変数の情報より意味があるということで、分散を1に規格化してマハラノビス距離で原点からの距離を算出し、固有値が1以下は誤差なので、分散を1に規格化してしまうと過大評価してしまうため、Q統計量（SPE）で距離を算出しております。
MSPCを実装する際はこの手法の方が良いです。

# 主成分は固有値が1以上の主成分を採用
for (i in 1:col_tra) {
  if (EV_tra[i] < 1) break      #固有値>=1はT2統計量、固有値<1はQ統計量
}
PC_tra <- (i-1)

# T2統計量の計算(学習データ)
# T2統計量は各主成分の主成分得点の2乗を各主成分の固有値で割って和をとる
EV_traT <- EV_tra[1:PC_tra]
evT <- matrix(rep(EV_traT,row_tra), ncol=PC_tra, byrow=TRUE)             #T2の固有値
T_tra <- score_tra[1:row_tra,1:PC_tra]*score_tra[1:row_tra,1:PC_tra]/evT #T2の計算
T2_tra <- apply(T_tra, 1, sum)

# Q統計量の計算(学習データ)
# Q統計量は各主成分の主成分得点の2乗の和をとる（推定値と観測値の2乗和）
EV_traQ <- EV_tra[(PC_tra+1):col_tra]
evQ <- matrix(rep(EV_traQ,row_tra), ncol=(col_tra-PC_tra), byrow=TRUE)
q_tra <- score_tra[1:row_tra,(PC_tra+1):col_tra]*score_tra[1:row_tra,(PC_tra+1):col_tra]
Q_tra <- apply(q_tra, 1, sum)

# 管理限界は学習データの99%を管理限界
calc_threshold_T2 <- density(T2_tra)
UCL_T2 <- quantile(calc_threshold_T2$x,0.99)
calc_threshold_Q <- density(Q_tra)
UCL_Q <- quantile(calc_threshold_Q$x,0.99)

次に評価データの処理を行います。

x_test <- fread("../data/test_data.csv")
col_test <- ncol(x_test)                          #変数の数
row_test <- nrow(x_test)                          #データ数
date_test <- x_test %>% select(1:2)
x_test <- x_test %>% select(3:col_test)
col_test <- ncol(x_test)                          #変数の数(再度）
x_test_std <- scale(x_test,apply(x_tra,2,mean),apply(x_tra,2,sd))   #標準化

PCAdata_tra_center <- t(x_tra_pca_center)
vector_tra <- as.matrix(vector_tra)
score_test <- scale(x_test,center=PCAdata_tra_center,scale=F) %*% vector_tra

# T2統計量の計算
PC_tra <- as.numeric(PC_tra)
estimated_test <- score_test[,1:PC_tra] %*% t(vector_tra)[1:PC_tra,] 
EV_traT <- as.matrix(EV_traT)
evT <- matrix(rep(EV_traT,row_test), ncol=PC_tra, byrow=TRUE)
T_test <- score_test[1:row_test,1:PC_tra]*score_test[1:row_test,1:PC_tra]/evT #T2値の計算
T2 <- apply(T_test, 1, sum)                #T2管理図
T2_test <- cbind(date_test,T2)             #T2管理図(日付付与）

# Q統計量の計算
error_test <- estimated_test - x_test
CP_Q_test_value <- error_test*error_test        #寄与プロット(CP_Q)
Q <- apply(CP_Q_test_value,1,sum)               #Ｑ管理図
CP_Q_test <- cbind(date_test,CP_Q_test_value)   #寄与プロット(日付付与）
Q_test <- cbind(date_test,Q)                    #Ｑ管理図(日付付与）

# 可視化のための加工
"&" <- function(e1, e2) {
    if (is.character(c(e1, e2))) {
        paste(e1, e2, sep = "")
    } else {
        base::"&"(e1, e2)
    }
}
mydata <- date_test %>% select(1:1)&" "&date_test %>% select(2:2)
date <- as.POSIXlt(mydata)  #日付の編集

# T2管理図とQ管理図を可視化
# 管理限界
UCL_T2 <- matrix(rep(UCL_T2,row_test), ncol=1, byrow=TRUE)
UCL_Q <- matrix(rep(UCL_Q,row_test), ncol=1, byrow=TRUE)

# T2管理図
MAX_T2 <- UCL_T2[1:1]*5
MAX_Q <- UCL_Q[1:1]*5
par(mfrow=c(1,1))
plot(date,T2,xlab = "time",ylim = c(0,MAX_T2),type="l",xaxt="n")
r <- as.POSIXct(round(range(date), "hours"))
axis.POSIXct(1, at=seq(r[1],r[2], by="5 day"), format="%m/%d", las = 3)
par(new=TRUE)
plot(UCL_T2,col="red",ylim = c(0,MAX_T2),xlab="",ylab="",type="l",xaxt="n")

# Q管理図
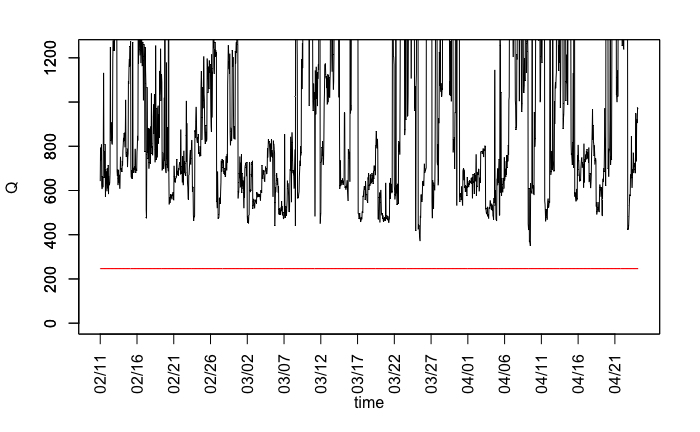
plot(date,Q,xlab = "time",ylim = c(0,MAX_Q),type="l",xaxt="n")
r <- as.POSIXct(round(range(date), "hours"))
axis.POSIXct(1, at=seq(r[1],r[2], by="5 day"), format="%m/%d", las = 3)
par(new=TRUE)
plot(UCL_Q,col="red",ylim = c(0,MAX_Q),xlab="",ylab="",type="l",xaxt="n")

$T^2$管理図は下記のようになります。

$Q$管理図は下記のようになります。

今回は追加で$T^2$管理図の寄与プロットを算出するコードも下記に記載します。

# T^2管理図の寄与プロット
score_tra_CM <- cov(score_tra)[1:PC_tra,1:PC_tra] ##主成分得点の共分散行列(学習)
V <- t(vector_tra)                                #負荷量行列の転置
EV_traT <- as.numeric(EV_traT)                    #変換
CP_T2_test_value <- (score_test[,1:PC_tra]%*%diag(1/EV_traT)%*%V[1:PC_tra,])*scale(x_test,center=PCAdata_tra_center,scale=F)
CP_T2_test <- cbind(date_test,CP_T2_test_value)   #T2寄与プロット(日付付与）

# 寄与プロット(T^2管理図)
UCL_T2_org <- UCL_T2[1:1]
par(mfrow=c(2,2))
par(mar = c(5, 5, 4, 4)) #  余白の広さを行数で指定．下，左，上，右の順．
for (j in 1:(row_test)){
  if (T2_test[[j,3]] >= UCL_T2_org)
    barplot(CP_T2_test_value[j,],ylab = "異常度", las = 3, main=date_test[j],cex.lab = 1.0,cex.main = 1.0,cex.names=0.3)
}

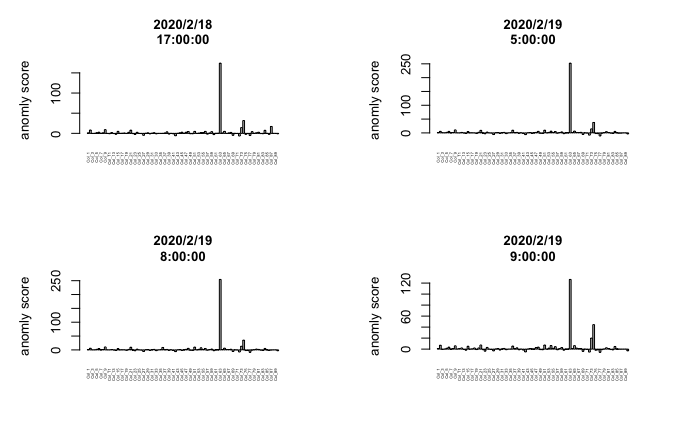
# 寄与プロット（Q管理図）
UCL_Q_org <- UCL_Q[1:1]
par(mfrow=c(2,2))
par(mar = c(5, 5, 4, 4)) #  余白の広さを行数で指定．下，左，上，右の順．
for (j in 1:(row_test)){
  if (Q_test[[j,3]] >= UCL_Q_org)
    barplot(CP_Q_test_value[j,],ylab = "異常度", las = 3, main=date_test[j],cex.lab = 1.0,cex.main = 1.0,cex.names=0.3)
}

さいごに

最後まで読んで頂き、ありがとうございました。
異常検知手法（MSPC）をRで実装しました。

訂正要望がありましたら、ご連絡頂けますと幸いです。