- 製造業出身のデータサイエンティストがお送りする記事
- 今回は、ベイジアンネットワークを活用して、因果探索を実装してみました。
はじめに
前回(統計的因果探索のLiNGAM)からの続きで、データから因果関係を推測するための機械学習技術の1つ「ベイジアンネットワーク」について整理しました。
細かい理論的な部分は省略します。
ベイジアンネットワークとは
ベイジアンネットワークは条件付き確率をベースに、変数間のグラフ構造を表現したものです。
ベイジアンネットワークの中でも、依存関係を算出する方法はいくつかありますが、今回は以下の方法を実施しました。
- 独立性の検定により、変数間のスケルトン(方向のない依存関係)を特定
- V-structure,オリエンテーションルールにより一部のスケルトンに方向を付与
上記はPCアルゴリズムと呼ばれる手法で、簡単に実装することができました。
今回もUCI Machine Learning Repositoryで公開されているボストン住宅の価格データを用いてベイジアンネットワークを構築します。
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート
import pandas as pd
import numpy as np
import networkx as nx
import os
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from pgmpy.models import BayesianModel
from pgmpy.estimators import ConstraintBasedEstimator
from pgmpy.estimators import BicScore
次にデータを読み込みます。
# データセットの読込み
boston = load_boston()
# データフレームの作成
# 説明変数の格納
df = pd.DataFrame(boston.data, columns = boston.feature_names)
# 目的変数の追加
df['MEDV'] = boston.target
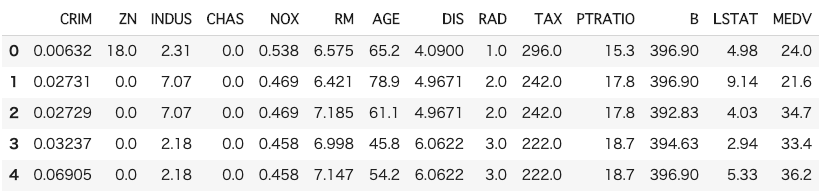
# データの中身を確認
df.head()
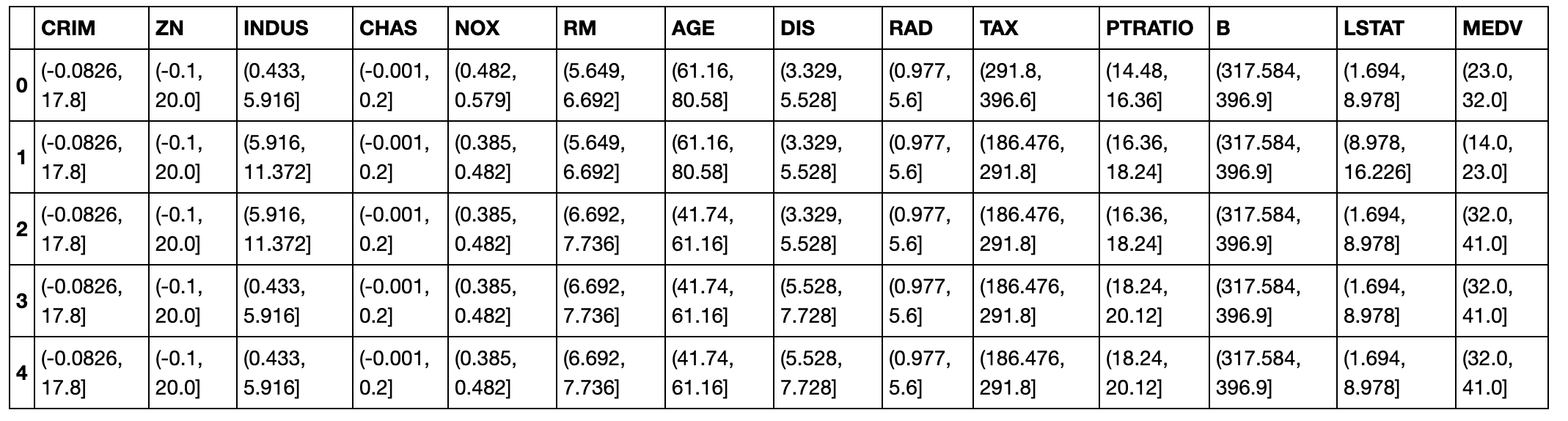
次に、PCアルゴリズムは連続値は扱えないため、離散値へ変更します。
# 離散値に変更
df_discrete = df.copy()
df_discrete['CRIM'] = pd.cut(df_discrete['CRIM'], 5)
df_discrete['ZN'] = pd.cut(df_discrete['ZN'], 5)
df_discrete['INDUS'] = pd.cut(df_discrete['INDUS'], 5)
df_discrete['CHAS'] = pd.cut(df_discrete['CHAS'], 5)
df_discrete['NOX'] = pd.cut(df_discrete['NOX'], 5)
df_discrete['RM'] = pd.cut(df_discrete['RM'], 5)
df_discrete['AGE'] = pd.cut(df_discrete['AGE'], 5)
df_discrete['DIS'] = pd.cut(df_discrete['DIS'], 5)
df_discrete['RAD'] = pd.cut(df_discrete['RAD'], 5)
df_discrete['TAX'] = pd.cut(df_discrete['TAX'], 5)
df_discrete['PTRATIO'] = pd.cut(df_discrete['PTRATIO'], 5)
df_discrete['B'] = pd.cut(df_discrete['B'], 5)
df_discrete['LSTAT'] = pd.cut(df_discrete['LSTAT'], 5)
df_discrete['MEDV'] = pd.cut(df_discrete['MEDV'], 5)
df_discrete.head()
ここから、ライブラリーpgmpyを用いてベイジアンネットワークを構築していきます。
est = ConstraintBasedEstimator(df_discrete)
skel, seperating_sets = est.estimate_skeleton(significance_level=0.01)
print("Undirected edges: ", skel.edges())
pdag = est.skeleton_to_pdag(skel, seperating_sets)
print("PDAG edges:", pdag.edges())
model = est.pdag_to_dag(pdag)
print("DAG edges:", model.edges())
各々算出されているものは下記を意味しております。
-
Undirected edgesは、方向性なし -
PDAG edgesは、部分的な方向性あり -
DAG edgesは、方向性あり
得られた結果は下記です。
Undirected edges: [('ZN', 'DIS'), ('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('NOX', 'DIS'), ('NOX', 'PTRATIO'), ('RM', 'MEDV'), ('AGE', 'LSTAT'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'PTRATIO'), ('LSTAT', 'MEDV')]
PDAG edges: [('ZN', 'DIS'), ('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('NOX', 'INDUS'), ('RM', 'MEDV'), ('AGE', 'LSTAT'), ('DIS', 'ZN'), ('DIS', 'NOX'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'INDUS'), ('TAX', 'RAD'), ('TAX', 'PTRATIO'), ('PTRATIO', 'INDUS'), ('PTRATIO', 'RAD'), ('LSTAT', 'AGE'), ('LSTAT', 'MEDV'), ('MEDV', 'RM'), ('MEDV', 'LSTAT')]
DAG edges: [('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('DIS', 'NOX'), ('DIS', 'ZN'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'PTRATIO'), ('LSTAT', 'AGE'), ('MEDV', 'RM'), ('MEDV', 'LSTAT')]
上記で基本的な処理は終了ですが、可視化してみないと分かりにくいので可視化しました。
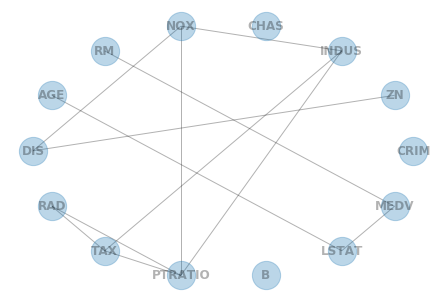
ただ、LiNGAMみたいに簡単に可視化してくれる方法がなかったため(あったら教えて欲しいです)、Undirected edges方向性なしと、DAG edges方向性ありだけ簡単に可視化しました。
# Undirected edges(方向性なし)可視化
G = nx.Graph()
G.add_nodes_from(df.columns) # ノード
G.add_edges_from(skel.edges()) # 辺
nx.draw_circular(G, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight='bold')
plt.show()
]:
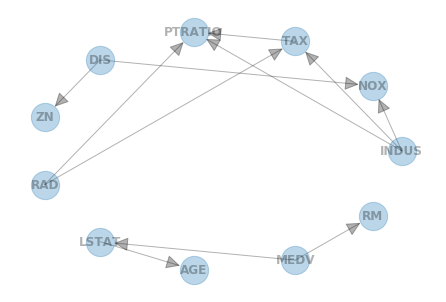
# DAG edges(方向性あり)可視化
DAG_model = BayesianModel(model.edges())
nx.draw_circular(DAG_model, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight='bold')
plt.show()
さいごに
最後まで読んで頂き、ありがとうございました。
ベイジアンネットワークも結構簡単に利用できることが分かりました。可視化の部分は、いまいち良い感じに実装できていないので、今後の課題です。
訂正要望がありましたら、ご連絡頂けますと幸いです。