0. はじめに
 1. 実行環境
 2. 逆運動学の解法
 3. 6自由度アームの幾何解法(理論)
3.0. 姿勢表現
 3.1. 逆運動学の解の確認(テスト)方法
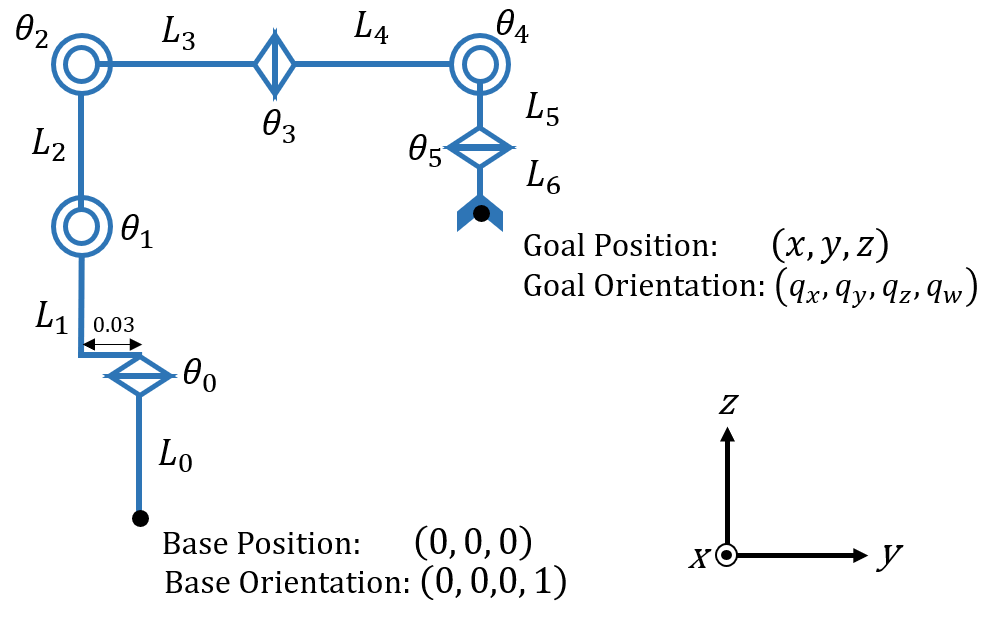
 3.2. 使用するロボットアーム
 3.3. ロボットアームモデルの簡略化
 - 他の構造表現方法(おまけ)
3.4. 特異点について
 4. 6自由度アームの幾何解法(実践)
4.0. パラメータと必要な関数の定義
 - パラメータの定義
 - 必要な関数の定義
 4.1. θ0を求める
 - 関節4の三次元位置[x4, y4, z4]を求める
 - 関節角度θ0を求める
 4.2. θ2を求める
 - 関節1の三次元位置[x1, y1, z1]を求める
 - 関節角度θ2を求める
 4.3. θ1を求める
 4.4. θ4を求める
 - 関節2の三次元位置[x2, y2, z2]を求める
 - 関節角度θ4を求める
 4.5. θ3を求める
 4.6. θ5を求める
 4.7. θ4の場合分け(重要)
4.8. 全体プログラム
 4.9. テスト
 5. Pybulletでのシミュレーション
 5.0. 方針
 5.1. 実行コード
 5.2. 実行結果
 6. 最後に

0. はじめに

　本記事ではロボットアームの逆運動学の解法の一つである幾何解法について解説しています。また、幾何解法によって解いた逆運動学の解を利用して、Pybulletでの仮想環境下で6自由度(6DoF)ロボットアームを動かしてシミュレーションによる検証を行いました。

　実際にPybulletでの動作確認を行いたいという方は、こちらの記事でPybulletの実装方法を解説しているので是非ご覧ください。

Pybulletでロボットアームシミュレーションをするまでの手順

　また、逆運動学の前に順運動学を知りたいという方はこちらをご覧ください。

Pybulletでロボットアームシミュレーション [順運動学を解いて6自由度アームの手先座標を求める]

　本記事では幾何解法について解説していますが、数値解法の方について知りたい方はこちらをご覧ください。

Pybulletでロボットアームシミュレーション [逆運動学を解いて6自由度アームで物体を掴む]

1. 実行環境

Windows10
WSL2
Ubuntu18.04

2. 逆運動学の解法

逆運動学の解法は大きく分けて数値解法と解析解法の２通りの方法があります。

解法	実装難易度	計算速度	計算精度
数値解法	〇	×	△
解析解法	×	〇	〇

　数値解法は、目標位置・姿勢に近づけるように関節角度を少しずつ調整していき、逐一計算することで最終的に解を求めるという方法です。
この手法の利点は、実装が比較的簡単であり、複雑な運動学のロボットアームでも解が出せることです。
しかし、計算に時間がかかることや、計算精度を上げると計算時間が増えるという欠点があります。

　解析解法は、数値解法とは対象的に数学的に逆運動学の解を求める手法です。
例としては、順運動学の式を変形や代入によって計算して逆運動学の解を求める代数的な解法や、ロボットアームのもつ幾何的な特徴を利用して各関節角度や位置、姿勢を求める幾何的な解法があります。
代数的な解法は、自由度の低い計算が楽なロボットアームの場合には有効な手段ですが、今回扱うような6自由度のロボットアームを解くとなると計算が厳しくなります。
一方、幾何的な解法は、代数的な解法よりも簡単な計算で関節角を求めることができるため、今回は幾何的にロボットアームの逆運動学を解いています。

　例えば下の図のようなロボットアームの肘関節の角度 $\theta$ を幾何的に求めたい場合、「腕・手の長さ・肩から手先までの長さ」の3つさえ分かれば余弦定理を使って $\cos{\theta}$ を求め、あとはコンピュータで $\arccos{(\cos{\theta})}$ を計算すれば $\theta$ が求まります。
このような計算を繰り返して解を求めていくのが、幾何的解法の基本的な流れです。

▼幾何解法

　解析解法の利点は、一度解が求まってしまえば逆運動学の解が一瞬で求まることと、計算精度が高いことの二つが挙げられます。
しかし、逆運動学の解は全て人の手で求めなくてはいけないため、実装するまでが大変という欠点があります。また、手計算で求める以上、場合分けミスや符号ミスなどが起こるため、順運動学の解と照らし合わせながら慎重に解を求める必要があります。
　そして解析解法のもう一つの欠点として、そもそも解析解法では求めることができないロボットが存在することです。とはいえ、通常ロボットアームは解析解法で解けるような形に設計されるため、基本的には問題ありません。ただ、もし完全に自作のロボットアームを作るようなことがあれば、このことに注意が必要です。

参考記事

機械工学辞典逆運動学

　以上のことから、**「計算速度は気にしないし超精密な動作は必要ないから、とにかく直ぐにロボットを動かしたい！」という場合は数値解法、「素早く正確にロボットを動かしたい！」**という場合は解析解法を選ぶと良いと思います。

3. 6自由度アームの幾何解法(理論)

　ここからは、6自由度のロボットアームを幾何的に解く方法について順番に説明していきます。先ほどは余弦定理を使ってロボットアームの肘関節角度を求めましたが、それだけでは6自由度アームを解くに不十分なため、空間ベクトルや順運動学の式などを活用して解きました。ただし、幾何的解法は決まった解き方があるわけではなく、ロボットアームの種類によっても解き方が変わってくるので注意が必要です。

3.0. 姿勢表現

　ロボットアームの運動学を解く際の重要な要素に姿勢表現の仕方がありますが、今回はクォータニオンを用いて解いています。
ここで言う姿勢とはいわゆる向きのことで、姿勢表現とはアームの手先がどの方向を向いているのかを表すということです。
クォータニオンは演算がしやすく、オイラー角のジンバルロックのような問題も起こらないとても便利な手法です。実際、UnityやPybulletの内部ではクォータニオンが使われているらしいので、これらを利用する方はクォータニオンを知っておくと良いと思います。

　クォータニオンの詳細については、こちらの記事が非常に参考になったのでご覧ください。

クォータニオン (Quaternion) を総整理！～三次元物体の回転と姿勢を鮮やかに扱う～

　姿勢表現の種類について知りたい方はこちらが参考になると思います。

回転ベクトル・回転行列・クォータニオン・オイラー角についてまとめてみた

3.1. 逆運動学の解の確認(テスト)方法

自分で逆運動学を解いた際には、自分で導出した解が本当に合っているかどうかを確認する必要があります。
逆運動学で出てくる解とはロボットアームの各関節角度のことですが、同じ手先位置・姿勢を取る関節角度の組み合わせは1通りとは限りません。(4.9. の図を参考)
そのため、逆運動学の解の確認をするには、

自分で導出した逆運動学の解を利用して順運動学を解き、手先位置・姿勢を出す
1. で出した手先位置・姿勢が、実際の手先位置・姿勢と重なっているかどうかを確認(テスト)する

という手順で行う必要があります。

詳しくは4.9. でプログラムを交えて説明しているので、そちらをご覧ください。

3.2. 使用するロボットアーム

　今回使用するロボットアームは、前回に引き続きデンソーVS-068というロボットアームの寸法を参考にして作成した自作モデルを使っていきます。

▼作成モデル

3.3. ロボットアームモデルの簡略化

　逆運動学の幾何解法はあくまで人の手で解いていく方法なので、作成したロボットアームモデルを眺めながら解くのでは少し考えにくいです。
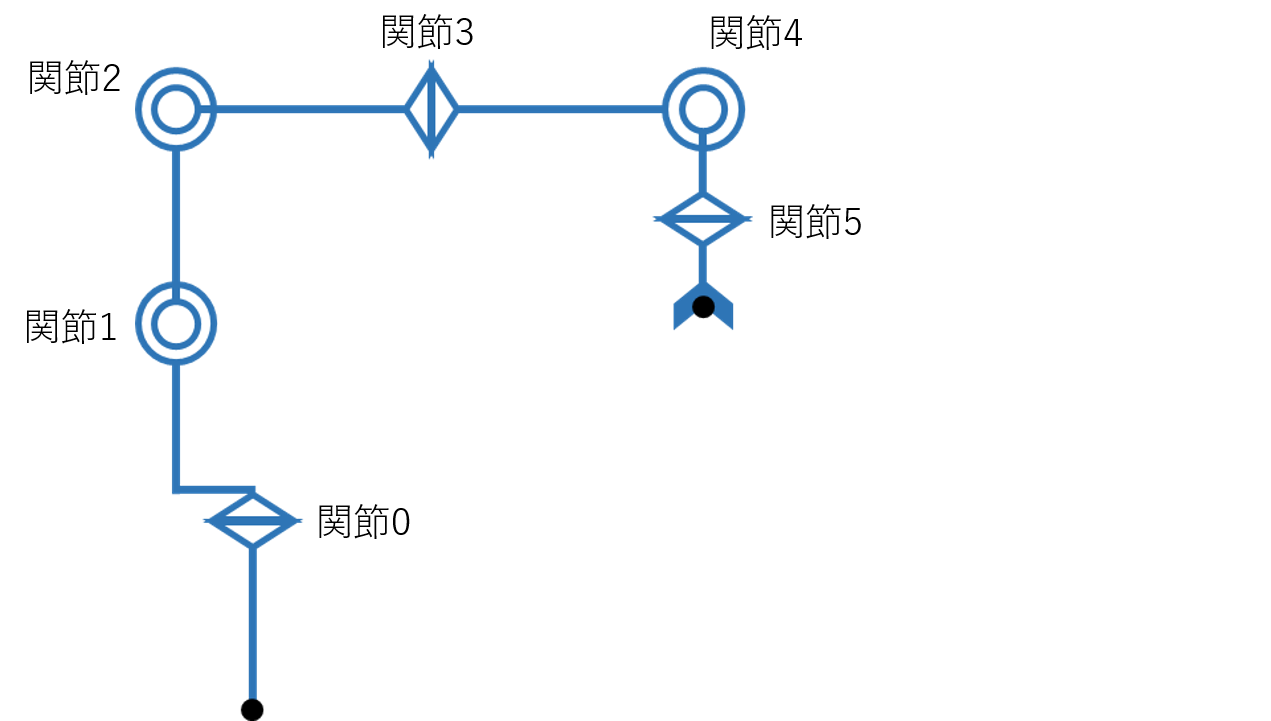
そのため、まずはモデルを数学的に考えやすい図に簡略化してみましょう。

▼簡略図

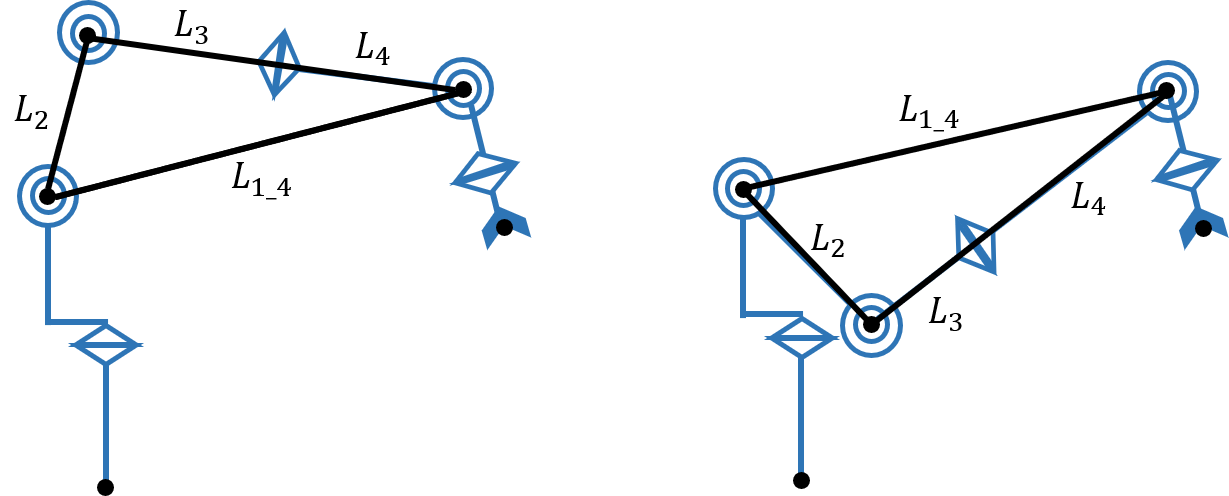
　ロボットアームモデルを簡略化すると上の図のようになります。
直線部分がアームを、円形やひし形のようなものが関節を表しています。このような図を描くことで、アームの構造・関節の位置と回転方向・原点の位置・手先の位置を簡単に読み取ることができます。

　回転関節については、回転・旋回・屈曲の3種類に分けられ、それぞれ下図のように描きます。
回転関節以外にもスライド式に動く直動関節などが存在しますが、今回使うロボットアームには使われていないので割愛します。

▼回転関節の種類

他の構造表現方法(おまけ)

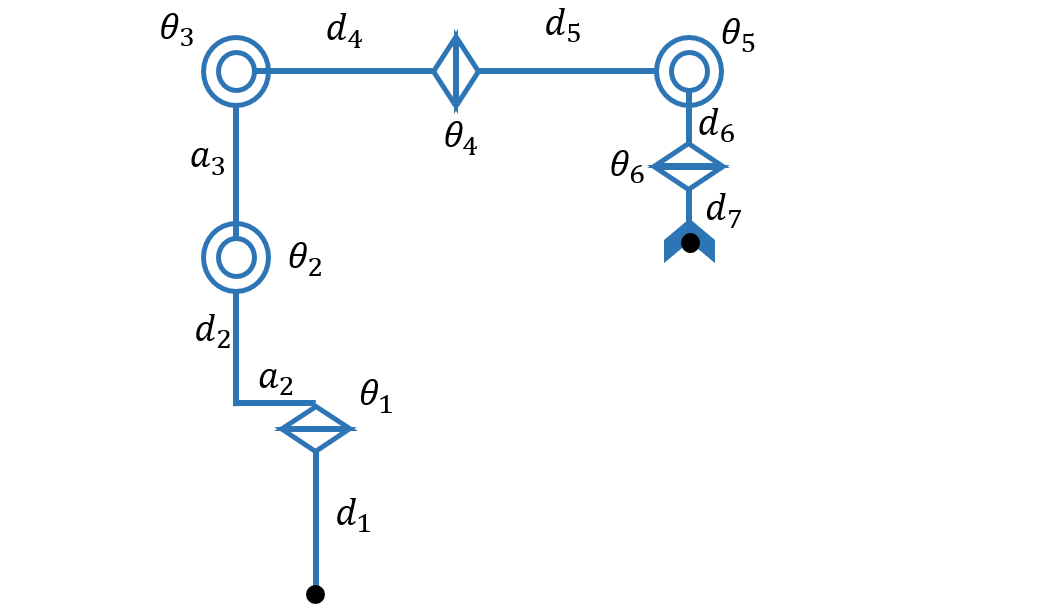
　本記事では主に先ほど説明した図を用いて解説をしていますが、ロボットアームの構造表現として**DHパラメータ (修正Denavit-Hartenberg記法)**という表を用いた方法も存在します。

簡単に説明すると、DHパラメータとは平行移動と回転移動の座標変換を各2回ずつ、計4回の座標変換のパラメータでロボットアームを表現する方法です。考え方としては同時座標変換行列に近いです。
座標変換の順番は、

X軸方向に $a$ だけ平行移動
Z軸回りに $\alpha$ だけ回転移動
Z軸方向に $d$ だけ平行移動
Z軸回りに $\theta$ だけ回転移動

となっています。
ここで言うX軸・Z軸は各リンクの座標系のことを指しているので、通常の空間座標と混同しないよう注意が必要です。
各リンクの座標軸の決め方、計算方法などの詳細については以下の記事をご参考下さい。

マニピュレータ - 東北学院大学情報処理センター

例えば今回使用するVS-068をDHパラメータで表現すると以下の表のようになります。

リンク	$a$	$\alpha$	$d$	$\theta$
1	$0$	$0$	$d_1$	$\theta_1$
2	$a_2$	$\frac{\pi}{2}$	$d_2$	$\theta_2$
3	$a_3$	$0$	$0$	$\theta_3$
4	$0$	$-\frac{\pi}{2}$	$d_4$	$\theta_4$
5	$0$	$\frac{\pi}{2}$	$d_5$	$\theta_5$
6	$0$	$-\frac{\pi}{2}$	$d_6$	$\theta_6$
7 (手先)	$0$	$0$	$d_7$	$0$

DHパラメータを図で見ると以下の通りです。
パラメータの定義の違いにより、 $\theta$ の添え字が先ほどの図とズレています。

▼DHパラメータ図示

3.4. 特異点について

　ロボットアームの運動学を解くときには特異点について必ず考える必要があります。
簡単に説明すると、特異点とはロボットアームの軸が2つ以上重なる状態のことです。この状態はロボットアームにとって非常に不味く、運動学を解く上で特異点出来るだけ避ける必要があります。

▼特異点

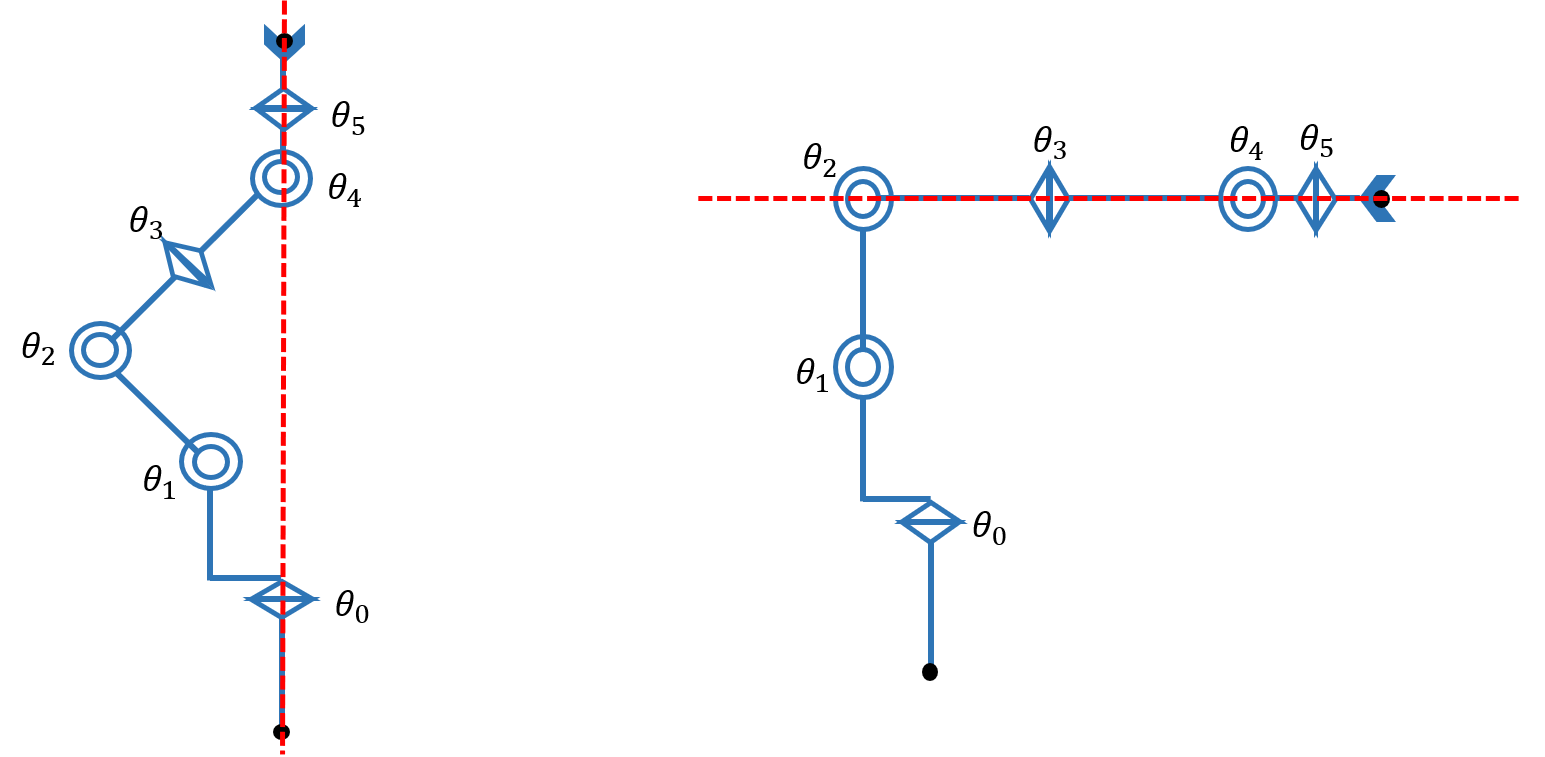
　特異点の問題の一つは、自由度が下がることです。関節の数は変化しないまま自由度が下がるということは、運動学の解が定まらなくなるということです。
例えば上図の左のような状態になると、 $\theta_0$ と $\theta_5$ の解が1つに定まりません。また、上図の右のような状態では $\theta_3$ と $\theta_5$ の解が1つに定まりません。そのため、特異点となった場合は無数にある関節角度の組み合わせの中で適切な解を人の手で設定する必要があります。

　また、数値解法で逆運動学を解く場合にも大きな問題が発生します。
逆運動学の数値解法ではヤコビアンという行列式で割る、という計算が出てきます。これは通常であれば問題なく計算できますが、特異点の状態のときヤコビアンの値は0になるため、エラーが起きてしまいます。結果的に、プログラムが完全に停止してしまったり、ロボットが暴走する原因となるので、数値解法では特異点を避けるようなプログラムが必要になります。

特異点についての詳細は以下の記事が参考になると思います。

ロボットの特異点を徹底解説！安定した動作に必要な回避方法も紹介

4. 6自由度アームの幾何解法(実践)

　さて、ここから実際に6自由度アームの逆運動学を幾何的に解いていきます。
先に方針を述べておくと、解法の流れは

関節4の位置を求める → 関節角度 $\theta_0$ を求める
関節1の位置を求める → 関節角度 $\theta_2$ を求める
関節角度 $\theta_1$ を求める
関節2の位置を求める → 関節角度 $\theta_4$ を求める
関節角度 $\theta_3$ を求める
関節角度 $\theta_5$ を求める
関節4の関節角度の場合分け処理

といったものになっています。

4.0. パラメータと必要な関数の定義

パラメータの定義

▼各パラメータ情報

計算するためのパラメータ設定として、各アームの長さを $L$ 、関節角度を $\theta$ 、手先位置を $[x, y, z]$ 、手先姿勢を $[q_x, q_y, q_z, q_w]$ と置きます。

また、図には書かれていませんが、各関節角の位置・姿勢は添え字表記で表します。
(例: 関節4の関節角度を $\theta_4$ 、位置を $[x_4, y_4, z_4]$ 、姿勢を $[q_{x4}, q_{y4}, q_{z4}, q_{w4}]$ と表記する)

必要な関数の定義

　6自由度アームの逆運動学を解くためには、順運動学の式が必要です。また、今回はクォータニオンで姿勢を表現するので、クォータニオンの演算を円滑にするための関数を定義しておいた方が効率が良いです。
そのため、逆運動学を解く前に順運動学やクォータニオンなどの関数を予め用意しておきます。

#順運動学の式を求める関数
def FK(L, js):
  Ts = []
  c0 = math.cos(js[0])
  s0 = math.sin(js[0])
  c1 = math.cos(js[1])
  s1 = math.sin(js[1])
  c2 = math.cos(js[2])
  s2 = math.sin(js[2])
  c3 = math.cos(js[3])
  s3 = math.sin(js[3])
  c4 = math.cos(js[4])
  s4 = math.sin(js[4])
  c5 = math.cos(js[5])
  s5 = math.sin(js[5])

  Ts.append(np.matrix([[c0, -s0, 0, 0], [s0, c0, 0, 0], [0, 0, 1, L[0]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c1, -s1, -0.03], [0, s1, c1, L[1]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c2, -s2, 0], [0, s2, c2, L[2]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[c3, -s3, 0, 0], [s3, c3, 0, 0], [0, 0, 1, L[3]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c4, -s4, 0], [0, s4, c4, L[4]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[c5, -s5, 0, 0], [s5, c5, 0, 0], [0, 0, 1, L[5]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, L[6]], [0, 0, 0, 1]]))

  return [Ts[0], Ts[0]*Ts[1], Ts[0]*Ts[1]*Ts[2], Ts[0]*Ts[1]*Ts[2]*Ts[3], Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4],
          Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4]*Ts[5], Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4]*Ts[5]*Ts[6]]

# クォータニオンを生成する関数
def make_q(L, theta):
  return [L[0]*math.sin(theta/2), L[1]*math.sin(theta/2), L[2]*math.sin(theta/2), math.cos(theta/2)]

# クォータニオンの積を計算する関数
def my_cross(q, p):
  return [q[3]*p[0] - q[2]*p[1] + q[1]*p[2] + q[0]*p[3],
          q[2]*p[0] + q[3]*p[1] - q[0]*p[2] + q[1]*p[3],
          -q[1]*p[0] + q[0]*p[1] + q[3]*p[2] + q[2]*p[3],
          -q[0]*p[0] - q[1]*p[1] - q[2]*p[2] + q[3]*p[3]]

# 各関節角度から手先姿勢を求める関数
def check_q(Theta):
  s53_0 = math.sin(Theta[5]/2 + Theta[3]/2 - Theta[0]/2)
  c53_0 = math.cos(Theta[5]/2 + Theta[3]/2 - Theta[0]/2)
  s5_3_0 = math.sin(Theta[5]/2 - Theta[3]/2 - Theta[0]/2)
  c5_3_0 = math.cos(Theta[5]/2 - Theta[3]/2 - Theta[0]/2)
  s3_0_5 = math.sin(Theta[3]/2 - Theta[0]/2 - Theta[5]/2)
  c3_0_5 = math.cos(Theta[3]/2 - Theta[0]/2 - Theta[5]/2)
  s530 = math.sin(Theta[5]/2 + Theta[3]/2 + Theta[0]/2)
  c530 = math.cos(Theta[5]/2 + Theta[3]/2 + Theta[0]/2)
  s12 = math.sin(Theta[1]/2 + Theta[2]/2)
  c12 = math.cos(Theta[1]/2 + Theta[2]/2)
  s4 = math.sin(Theta[4]/2)
  c4 = math.cos(Theta[4]/2)

  return [c53_0*c4*s12 + c5_3_0*s4*c12,
          -s53_0*c4*s12 - s5_3_0*s4*c12,
          s3_0_5*s4*s12 + s530*c4*c12,
          -c3_0_5*s4*s12 + c530*c4*c12]

# θの範囲を[-π, π]に直す関数
def fixPi(Js):
  js = Js
  for j in range(len(Js)):
    if js[j] > math.pi:
      js[j] = js[j] - int((js[j] + math.pi)/(2*math.pi))*2*math.pi
    elif js[j] < -math.pi:
      js[j] = js[j] - int((js[j]-math.pi)/(2*math.pi))*2*math.pi
  return js

4.1. θ0を求める

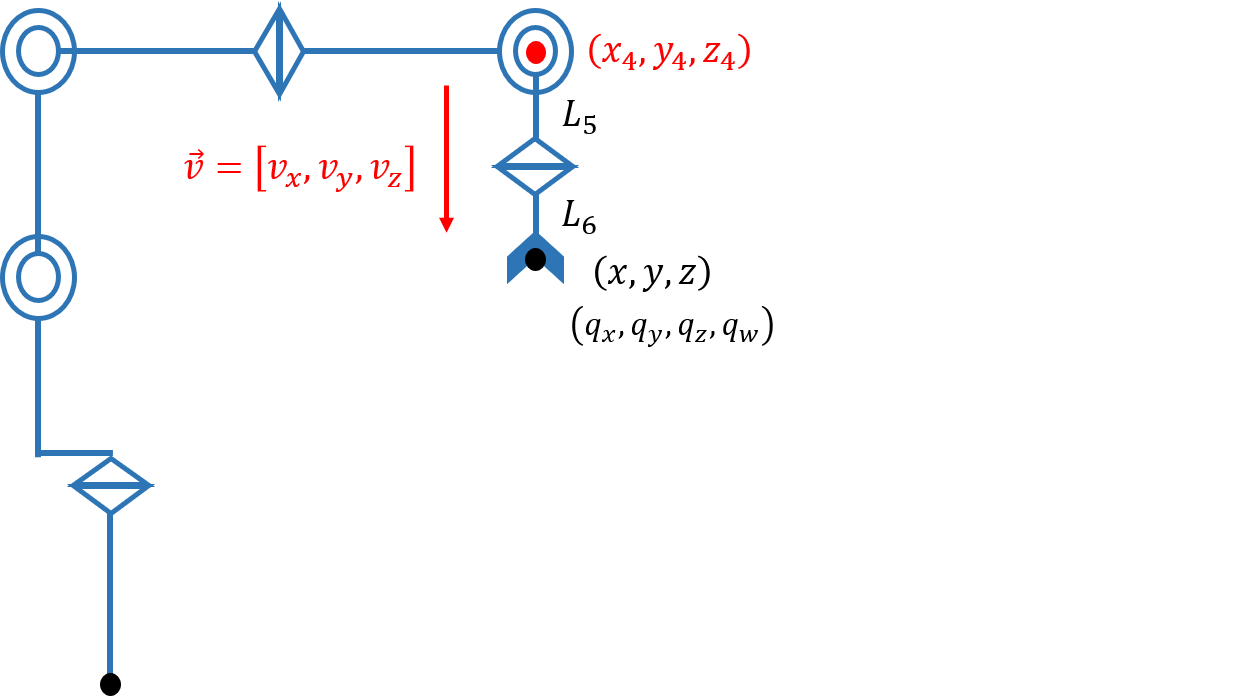
関節4の三次元位置[x4, y4, z4]を求める

▼ $[x_4, y_4, z_4]$ の求解

　$[x_4, y_4, z_4]$ を求めるために空間ベクトルを用います。
手先姿勢が分かっているのでクォータニオンの演算から簡単に $\vec{v}$ を求めることができます。

z軸方向の単位ベクトルを \ \vec{n_z} = [0,\ 0,\ 1] \ とする.\\
\vec{v} = q\otimes \vec{n_z} \otimes \bar{q}\\
=[2 ( q_xq_z + q_yq_w),\ 2 ( q_yq_z - q_xq_w),\ -q_x^2 - q_y^2 + q_z^2 + q_w^2]

　$\vec{v}$ さえ求まれば、アームの長さ $L_4$, $L_5$ は分かっているので、次式のようにして $[x_4, y_4, z_4]$ を得ることができます。

[x_4, y_4, z_4] = [x, y, z]-(L_4 + L_5)\vec{v}

L = [0.1975, 0.1975, 0.340, 0.197, 0.143, 0.070, 0.035] #アームの長さ
q = quaternion #手先姿勢[qx, qy, qz, qw]

vx = 2*(q[0]*q[2] + q[3]*q[1])
vy = 2*(q[1]*q[2] - q[3]*q[0])
vz = q[3]**2 - q[0]**2 - q[1]**2 + q[2]**2

x4 = x - (L[5] + L[6])*vx
y4 = y - (L[5] + L[6])*vy
z4 = z - (L[5] + L[6])*vz

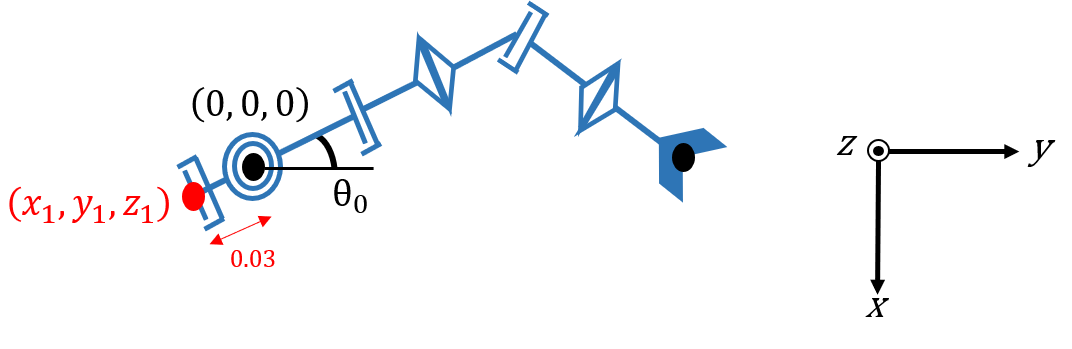
関節角度θ0を求める

▼簡略図 (xy平面)

　ロボットアームをxy平面上で見ると上図のようになります。
この図から、原点から $[x_4, y_4, z_4]$ にかけてアームが同一直線上に位置していることが分かります。つまり、原点から $[x_4, y_4, z_4]$ までの角度を求めれば$\theta_0$ が導出できるということです。
この角度は $\arctan{}$ で簡単に求められますが、上図ではx軸が下方向、y軸が右方向に向いていることに注意が必要です。

\theta_0 = \arctan(\frac{y_4}{-x_4})

また、 $[x, y]=[0,0]$ のときの場合分けをしておきます。この場合分けをすることで、特異点にも対処できます。

if x4==0 and y4==0:
  Theta0 = 0
else:
  Theta0 = math.atan2(-x4, y4)

4.2. θ2を求める

関節1の三次元位置[x1, y1, z1]を求める

▼ $[x_1, y_1, z_1]$ の求解

　$\theta_0$ が求まったので、 $[x_1, y_1, z_1]$ が求まります。

x_1 = 0.03\sin(\theta_0)\\
x_1 = - 0.03\cos(\theta_0)\\
z_1 = L_0 + L_1

x1 = 0.03*math.sin(Theta0)
y1 = -0.03*math.cos(Theta0)
z1 = L[0] + L[1]

関節角度θ2を求める

▼ $\theta_2$ の求解

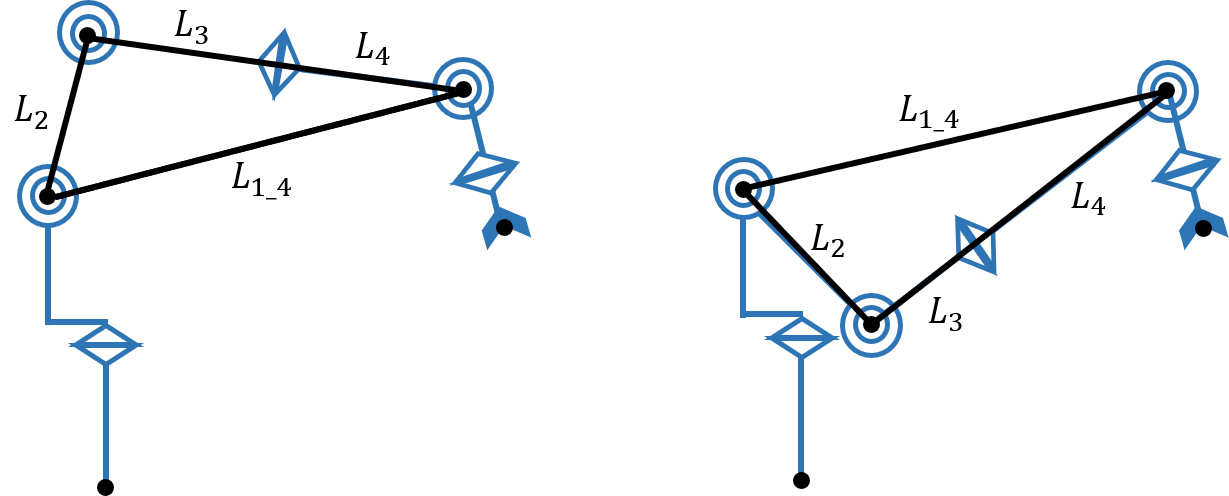
　$\theta_2$ は余弦定理を用いて導出することができます。ただし、 $\theta_2$ の位置が三角形の外角側であることに注意します。

余弦定理より, \\
\cos( 180^\circ - \theta_2 ) = \frac{L_2^2 + (L_3 + L_4)^2 - L_{1\_4}^2}{2L_2(L_3 + L_4)}\\
\theta_2 = \arccos\biggl(-\frac{L_2^2 + (L_3 + L_4)^2 - L_{1\_4}^2}{2L_2(L_3 + L_4)}\biggr)

　また、余弦定理だけでは下図のような山形と谷形の二通りの解が想定されるため、解を一つに絞ります。今回は図の左側のようなアームが山形になる解を選ぶことにします。

▼二通りのアーム角度

L14 = math.sqrt((x4 - x1)**2 + (y4 - y1)**2 + (z4 - (L[0] + L[1]))**2)
Theta2 = math.acos(-(L[2]**2 + (L[3] + L[4])**2 - L14**2)/(2*L[2]*(L[3] + L[4])))

4.3. θ1を求める

▼ $\theta_1$ の求解

　$\theta_1$ も同様に余弦定理から求めることができます。
上図のように、余弦定理から $\theta_{\verb|1_1|}$ と $\theta_{\verb|1_2|}$ を求め、その和から $\theta_1$ を得ることができます。

Theta1_1 = math.acos((L[2]**2 + L14**2 - (L[3] + L[4])**2)/(2*L[2]*L14))
L04_ = math.sqrt((x4 - x1)**2 + (y4 - y1)**2 + (z4 - L[0])**2)
Theta1_2 = math.acos((L[1]**2 + L14**2 - L04_**2)/(2*L[1]*L14))
Theta1 = math.pi - (Theta1_1 + Theta1_2)

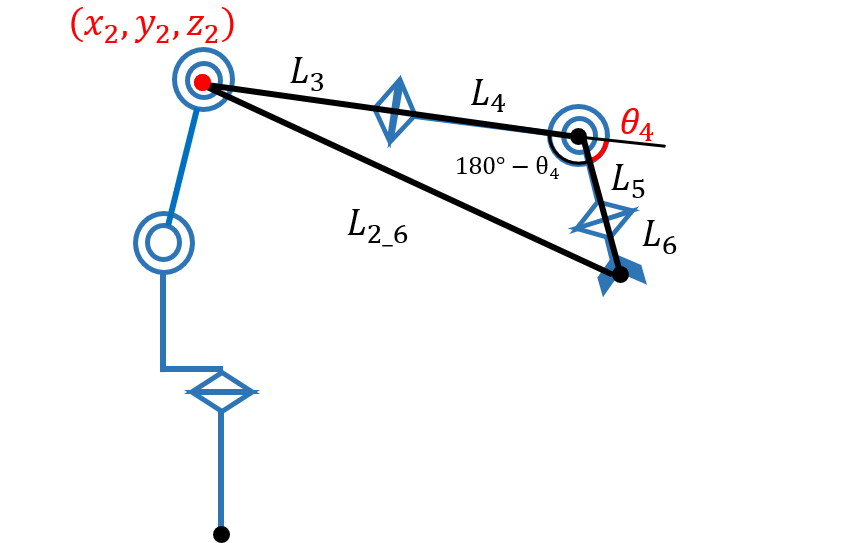
4.4. θ4を求める

関節2の三次元位置[x2, y2, z2]を求める

▼ $\theta_4$ の求解

　$\theta_4$ は $[x_2, y_2, z_2]$ を求めれば余弦定理で導出することができます。
まずは順運動学の式から $[x_2, y_2, z_2]$ を求めます。

#θ0とθ1が分かれば[x2, y2, z2]が求まる
xyz2 = FK(L, [Theta0, Theta1, 0, 0, 0, 0])
x2 = xyz2[2][0, 3]
y2 = xyz2[2][1, 3]
z2 = xyz2[2][2, 3]

関節角度θ4を求める

　$[x_2, y_2, z_2]$ が求まったので、余弦定理から $\theta_4$ が求まります。

L26_2 = (x - x2)**2 + (y - y2)**2 + (z - z2)**2 #L26の2乗
Theta4 = math.acos(-((L[3] + L[4])**2 + (L[5] + L[6])**2 - L26_2)/(2*(L[3] + L[4])*(L[5] + L[6])))

4.5. θ3を求める

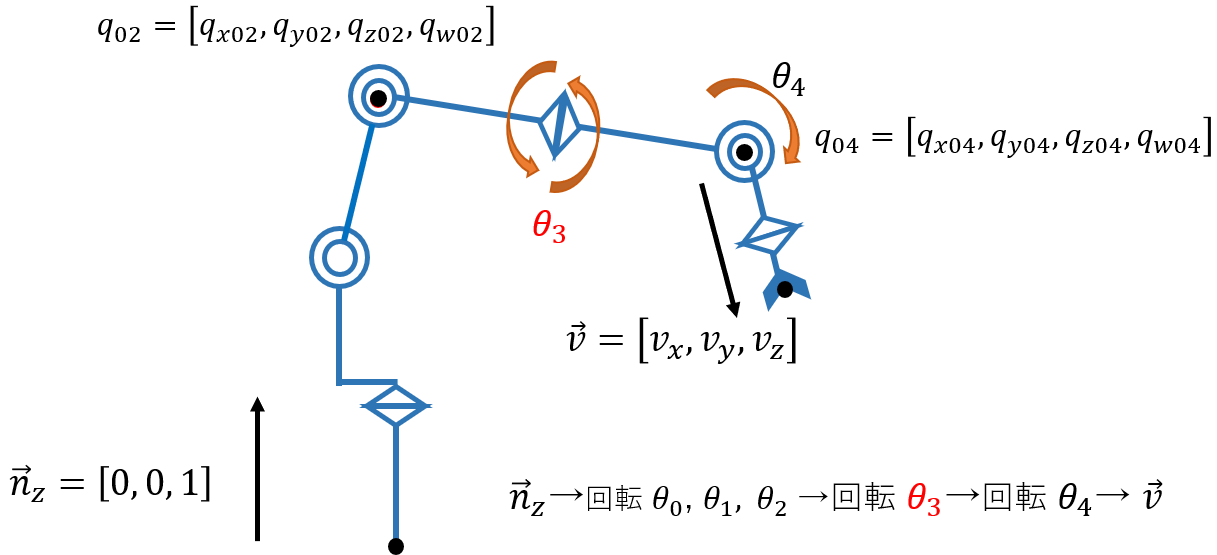
　$\theta_3$ は姿勢を変更するための回転関節なので、今までのように余弦定理で求めることはできません。 $\theta_3$ を求めるためには位置ではなく姿勢の情報、つまりクォータニオンを用います。

▼ $\theta_3$ の求解

　考え方としては最初の1-1で $[x_4, y_4, z_4]$ を求めたときと同じです。
クォータニオンの姿勢が分かっていれば、その位置でのロボットアームの方向(空間ベクトル)を計算することができます。
そのため、

$\theta_0$, $\theta_1$, $\theta_2$から関節2でのアームの姿勢 $q_{02}$ を求める
$q_{02}$ に対しある回転 $\theta_3$ と既知の回転 $\theta_4$ を加えることで $q_{04}$ を求める
姿勢 $q_{04}$ からベクトル $\vec{v}$ を求める式をつくる( $\vec{v} = q_{04} \otimes \vec{n_z} \otimes \bar{q}_{04}$ )
3.で立てた方程式から $\theta_3$ を求める

という流れで $\theta_3$ を求めることができます。

クォータニオンの計算方法については、先ほども紹介しましたがこちらの記事をご参照ください。

クォータニオン (Quaternion) を総整理！～三次元物体の回転と姿勢を鮮やかに扱う～

計算を進めると、最終的には以下の方程式に落ち着きます。 $q_{02}$, $\theta_4$, $\vec{v}$ の値については既知であるため、 $\theta_3$ が求まります。

q_{02} = [q_x, q_y, q_z, q_w], \ \vec{v} = [v_x, v_y, v_z] \ とする. \\
\begin{pmatrix}
2(q_{z}q_{w} - q_{x}q_{y})\sin{\theta_4} & ({q_{x}}^2 - {q_{y}}^2 - {q_{z}}^2 + {q_{w}}^2)\sin{\theta_4} \\
({q_{x}}^2 - {q_{y}}^2 + {q_{z}}^2 - {q_{w}}^2)\sin{\theta_4} & 2(q_{z}q_{w} + q_{x}q_{y})\sin{\theta_4}
\end{pmatrix}
\begin{pmatrix}
\cos{\theta_3}\\
\sin{\theta_3}
\end{pmatrix}
=
\begin{pmatrix}
v_x - 2(q_{x}q_{z} + q_{y}q_{w})\cos{\theta_4}\\
v_y - 2(q_{y}q_{z} - q_{x}q_{w})\cos{\theta_4}
\end{pmatrix}

#関節角度, 回転軸からクォータニオンq0, q1, q2をつくる
my_q = []
my_q.append(make_q([0,0,1], Theta0))
my_q.append(make_q([1,0,0], Theta1))
my_q.append(make_q([1,0,0], Theta2))

#クォータニオンq0, q1, q2の積を取りq02を得る
my_Q = []
my_Q.append(my_cross(my_q[0], my_q[1]))
my_Q.append(my_cross(my_Q[0], my_q[2]))
qx02 = my_Q[1][0]
qy02 = my_Q[1][1]
qz02 = my_Q[1][2]
qw02 = my_Q[1][3]

C4 = math.cos(Theta4)
S4 = math.sin(Theta4)

# 方程式を解いてθ3を得る(方程式の導出過程は省略)
A = np.matrix([[2*(qz02*qw02 - qx02*qy02)*S4, (qx02**2 - qy02**2 - qz02**2 + qw02**2)*S4],
               [(qx02**2 - qy02**2 + qz02**2 - qw02**2)*S4, 2*(qw02*qz02 + qx02*qy02)*S4]])
B = np.matrix([[vx - 2*(qz02*qx02 + qw02*qy02)*C4], [vy - 2*(qy02*qz02 - qx02*qw02)*C4]])
invA = np.linalg.inv(A)
XY = invA*B
Theta3 = math.atan2(XY[1], XY[0])

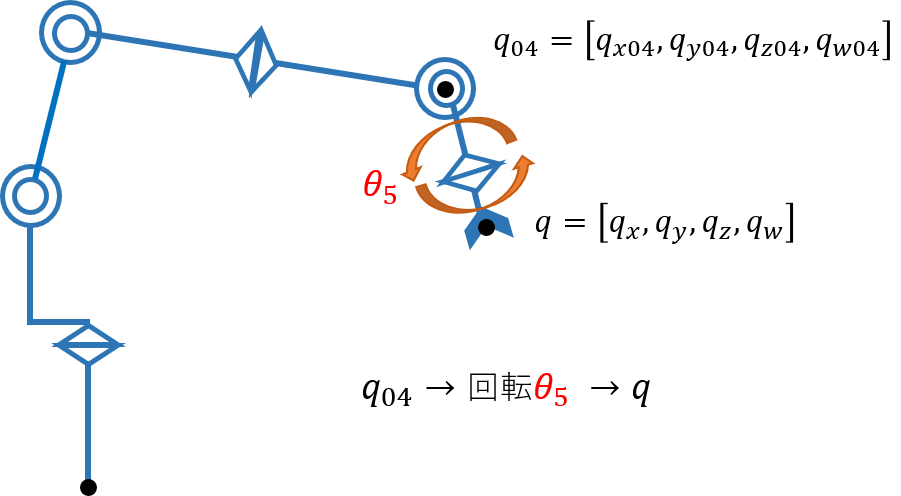
4.6. θ5を求める

▼ $\theta_5$ の求解

　最後に $\theta_5$ を求めます。これまでの計算で $\theta_0$ ~ $\theta_4$ までの関節角度は分かっているので、

$\theta_0$ ~ $\theta_4$ から $q_{04}$ を求める
$q_{04}$ に対しある回転 $\theta_5$ を加えることで $q$ を求める式をつくる
1. で立てた方程式から $\theta_5$ を求める

という流れで $\theta_5$ を求めます。
ちなみに、先に $\theta_3$ から求めている影響で、特異点の場合には$\theta_5=0$ になります。

#q3, q4をつくる
my_q.append(make_q([0,0,1], Theta3))
my_q.append(make_q([1,0,0], Theta4))

#q04を得る
my_Q.append(my_cross(my_Q[1], my_q[3]))
my_Q.append(my_cross(my_Q[2], my_q[4]))
qx04 = my_Q[3][0]
qy04 = my_Q[3][1]
qz04 = my_Q[3][2]
qw04 = my_Q[3][3]

# 手先姿勢quaternion
qx5 = q[0]
qy5 = q[1]
qz5 = q[2]
qw5 = q[3]

# 方程式を解いてθ5を得る(方程式の導出過程は省略)
C5 = (qx04*qx5 + qy04*qy5)/(qx04**2 + qy04**2)
S5 = (qx5*qy04 - qy5*qx04)/(qx04**2 + qy04**2)
Theta5 = 2*math.atan2(S5, C5)

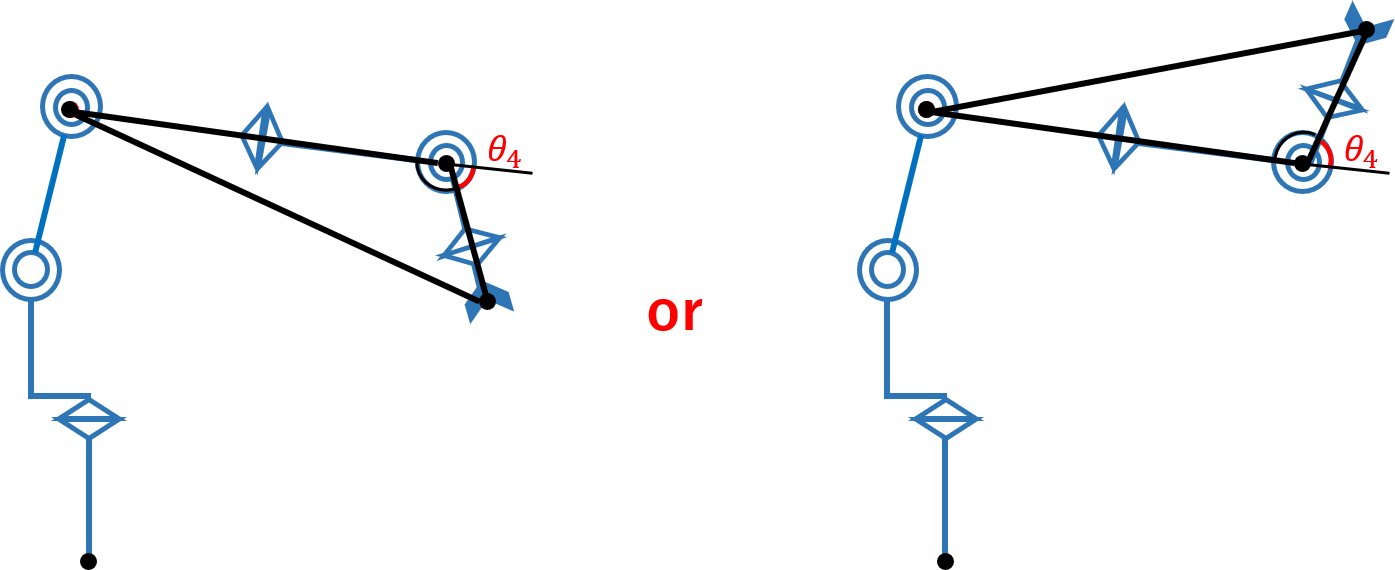
4.7. θ4の場合分け(重要)

　4.6. までで無事全ての関節角度を導出することに成功しましたが、実はこれだけでは不完全です。
4.4. で $\theta_4$ を求めたときに余弦定理を用いましたが、余弦定理だけでは下図のような2通りの場合について対応することができません。

▼2通りのパターン　

$\theta_4$ を求めたときに用いた math.acos() は $[0, \pi]$ の範囲で値を返す関数なので、上図でいうと左側のパターン( $\theta_4>0$ )にしか対応していません。
そのため、

$\theta_4>0$ と仮定して全ての関節角度を求め、順運動学から手先位置・姿勢を求める
1. の結果が実際の手先位置・姿勢と一致していたら終了
一致しなかった場合、$\theta_4→-\theta_4$ に符号を変更して、残りの関節角度を改めて求め直す

といった方法で場合分けを行います。

#各関節角度js
js = fixPi([Theta0, Theta1, Theta2, Theta3, Theta4, Theta5])

#逆運動学を解いて出した手先姿勢check_qtn
check_qtn = check_q(js)

if quaternion[0]*check_qtn[0] > 0: #手先姿勢が正しい値と一致した場合
  return js
else:  #手先姿勢が一致しない場合
  Theta4_ = -Theta4

4.8. 全体プログラム

　章の最後に、全体プログラムを記載しておきます。
全体を通してプログラムを読みたい方、コードを参考にしたい方はご覧ください。

全体プログラム (**クリックして表示**)

AnalyticSolution.py

import numpy as np
import math
import random

#順運動学の式を求める関数
def FK(L, js):
  Ts = []
  c0 = math.cos(js[0])
  s0 = math.sin(js[0])
  c1 = math.cos(js[1])
  s1 = math.sin(js[1])
  c2 = math.cos(js[2])
  s2 = math.sin(js[2])
  c3 = math.cos(js[3])
  s3 = math.sin(js[3])
  c4 = math.cos(js[4])
  s4 = math.sin(js[4])
  c5 = math.cos(js[5])
  s5 = math.sin(js[5])

  Ts.append(np.matrix([[c0, -s0, 0, 0], [s0, c0, 0, 0], [0, 0, 1, L[0]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c1, -s1, -0.03], [0, s1, c1, L[1]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c2, -s2, 0], [0, s2, c2, L[2]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[c3, -s3, 0, 0], [s3, c3, 0, 0], [0, 0, 1, L[3]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, c4, -s4, 0], [0, s4, c4, L[4]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[c5, -s5, 0, 0], [s5, c5, 0, 0], [0, 0, 1, L[5]], [0, 0, 0, 1]]))
  Ts.append(np.matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, L[6]], [0, 0, 0, 1]]))

  return [Ts[0], Ts[0]*Ts[1], Ts[0]*Ts[1]*Ts[2], Ts[0]*Ts[1]*Ts[2]*Ts[3], Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4],
          Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4]*Ts[5], Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4]*Ts[5]*Ts[6]]

#クォータニオンを生成する関数
def make_q(L, theta):
  return [L[0]*math.sin(theta/2), L[1]*math.sin(theta/2), L[2]*math.sin(theta/2), math.cos(theta/2)]

#クォータニオンの積を計算する関数
def my_cross(q, p):
  return [q[3]*p[0] - q[2]*p[1] + q[1]*p[2] + q[0]*p[3],
          q[2]*p[0] + q[3]*p[1] - q[0]*p[2] + q[1]*p[3],
          -q[1]*p[0] + q[0]*p[1] + q[3]*p[2] + q[2]*p[3],
          -q[0]*p[0] - q[1]*p[1] - q[2]*p[2] + q[3]*p[3]]

#各関節角度から手先姿勢を求める関数
def check_q(Theta):
  s53_0 = math.sin(Theta[5]/2 + Theta[3]/2 - Theta[0]/2)
  c53_0 = math.cos(Theta[5]/2 + Theta[3]/2 - Theta[0]/2)
  s5_3_0 = math.sin(Theta[5]/2 - Theta[3]/2 - Theta[0]/2)
  c5_3_0 = math.cos(Theta[5]/2 - Theta[3]/2 - Theta[0]/2)
  s3_0_5 = math.sin(Theta[3]/2 - Theta[0]/2 - Theta[5]/2)
  c3_0_5 = math.cos(Theta[3]/2 - Theta[0]/2 - Theta[5]/2)
  s530 = math.sin(Theta[5]/2 + Theta[3]/2 + Theta[0]/2)
  c530 = math.cos(Theta[5]/2 + Theta[3]/2 + Theta[0]/2)
  s12 = math.sin(Theta[1]/2 + Theta[2]/2)
  c12 = math.cos(Theta[1]/2 + Theta[2]/2)
  s4 = math.sin(Theta[4]/2)
  c4 = math.cos(Theta[4]/2)

  return [c53_0*c4*s12 + c5_3_0*s4*c12,
          -s53_0*c4*s12 - s5_3_0*s4*c12,
          s3_0_5*s4*s12 + s530*c4*c12,
          -c3_0_5*s4*s12 + c530*c4*c12]

#θの範囲を[-π, π]に直す関数
def fixPi(Js):
  js = Js
  for j in range(len(Js)):
    if js[j] > math.pi:
      js[j] = js[j] - int((js[j] + math.pi)/(2*math.pi))*2*math.pi
    elif js[j] < -math.pi:
      js[j] = js[j] - int((js[j]-math.pi)/(2*math.pi))*2*math.pi
  return js

#手先位置[x, y, z], 手先姿勢quaternionから各関節角度jsを求める関数
def AnalyticSolution(x, y, z, quaternion):
  L = [0.1975, 0.1975, 0.340, 0.197, 0.143, 0.070, 0.035] #アームの長さ
  q = quaternion #手先姿勢[qx, qy, qz, qw]

  vx = 2*(q[0]*q[2] + q[3]*q[1])
  vy = 2*(q[1]*q[2] - q[3]*q[0])
  vz = q[3]**2 - q[0]**2 - q[1]**2 + q[2]**2

  x4 = x - (L[5] + L[6])*vx
  y4 = y - (L[5] + L[6])*vy
  z4 = z - (L[5] + L[6])*vz

  if x4==0 and y4==0:
    Theta0 = 0
  else:
    Theta0 = math.atan2(-x4, y4)

  x1 = 0.03*math.sin(Theta0)
  y1 = -0.03*math.cos(Theta0)
  z1 = L[0] + L[1]

  L14 = math.sqrt((x4 - x1)**2 + (y4 - y1)**2 + (z4 - (L[0] + L[1]))**2)
  Theta2 = math.acos(-(L[2]**2 + (L[3] + L[4])**2 - L14**2)/(2*L[2]*(L[3] + L[4])))

  Theta1_1 = math.acos((L[2]**2 + L14**2 - (L[3] + L[4])**2)/(2*L[2]*L14))
  L04_ = math.sqrt((x4 - x1)**2 + (y4 - y1)**2 + (z4 - L[0])**2)
  Theta1_2 = math.acos((L[1]**2 + L14**2 - L04_**2)/(2*L[1]*L14))
  Theta1 = math.pi - (Theta1_1 + Theta1_2)

  #θ0とθ1が分かれば[x2, y2, z2]が求まる
  xyz2 = FK(L, [Theta0, Theta1, 0, 0, 0, 0])
  x2 = xyz2[2][0, 3]
  y2 = xyz2[2][1, 3]
  z2 = xyz2[2][2, 3]

  L26_2 = (x - x2)**2 + (y - y2)**2 + (z - z2)**2 #L26の2乗
  Theta4 = math.acos(-((L[3] + L[4])**2 + (L[5] + L[6])**2 - L26_2)/(2*(L[3] + L[4])*(L[5] + L[6])))

  #関節角度, 回転軸からクォータニオンq0, q1, q2をつくる
  my_q = []
  my_q.append(make_q([0,0,1], Theta0))
  my_q.append(make_q([1,0,0], Theta1))
  my_q.append(make_q([1,0,0], Theta2))

  #クォータニオンq0, q1, q2の積を取りq02を得る
  my_Q = []
  my_Q.append(my_cross(my_q[0], my_q[1]))
  my_Q.append(my_cross(my_Q[0], my_q[2]))
  qx02 = my_Q[1][0]
  qy02 = my_Q[1][1]
  qz02 = my_Q[1][2]
  qw02 = my_Q[1][3]

  C4 = math.cos(Theta4)
  S4 = math.sin(Theta4)

  #方程式を解いてθ3を得る(方程式の導出過程は省略)
  A = np.matrix([[2*(qz02*qw02 - qx02*qy02)*S4, (qx02**2 - qy02**2 - qz02**2 + qw02**2)*S4],
                 [(qx02**2 - qy02**2 + qz02**2 - qw02**2)*S4, 2*(qw02*qz02 + qx02*qy02)*S4]])
  B = np.matrix([[vx - 2*(qz02*qx02 + qw02*qy02)*C4], [vy - 2*(qy02*qz02 - 
  qx02*qw02)*C4]])
  invA = np.linalg.inv(A)
  XY = invA*B
  Theta3 = math.atan2(XY[1], XY[0])

  #q3, q4をつくる
  my_q.append(make_q([0,0,1], Theta3))
  my_q.append(make_q([1,0,0], Theta4))

  #q04を得る
  my_Q.append(my_cross(my_Q[1], my_q[3]))
  my_Q.append(my_cross(my_Q[2], my_q[4]))
  qx04 = my_Q[3][0]
  qy04 = my_Q[3][1]
  qz04 = my_Q[3][2]
  qw04 = my_Q[3][3]

  #手先姿勢quaternion
  qx5 = q[0]
  qy5 = q[1]
  qz5 = q[2]
  qw5 = q[3]

  #方程式を解いてθ5を得る(方程式の導出過程は省略)
  C5 = (qx04*qx5 + qy04*qy5)/(qx04**2 + qy04**2)
  S5 = (qx5*qy04 - qy5*qx04)/(qx04**2 + qy04**2)
  Theta5 = 2*math.atan2(S5, C5)

  #各関節角度js
  js = fixPi([Theta0, Theta1, Theta2, Theta3, Theta4, Theta5])

  #逆運動学を解いて出した手先姿勢check_qtn
  check_qtn = check_q(js)

  if quaternion[0]*check_qtn[0] > 0: #手先姿勢が正しい値と一致した場合
    return js
  else:  #手先姿勢が一致しない場合
    Theta4_ = -Theta4

    qx02 = my_Q[1][0]
    qy02 = my_Q[1][1]
    qz02 = my_Q[1][2]
    qw02 = my_Q[1][3]
    C4_ = math.cos(Theta4_)
    S4_ = math.sin(Theta4_)

    A_ = np.matrix([[2*(qz02*qw02 - qx02*qy02)*S4_, (qx02**2 - qy02**2 - qz02**2 + qw02**2)*S4_],
                [(qx02**2 - qy02**2 + qz02**2 - qw02**2)*S4_, 2*(qw02*qz02 + qx02*qy02)*S4_]])
    B_ = np.matrix([[vx - 2*(qz02*qx02 + qw02*qy02)*C4_], [vy - 2*(qy02*qz02 - qx02*qw02)*C4_]])
    invA_ = np.linalg.inv(A_)
    XY_ = invA_*B_
    Theta3_ = math.atan2(XY_[1], XY_[0])

    my_q_ = []
    my_q_.append(make_q([0, 0, 1], Theta0))
    my_q_.append(make_q([1, 0, 0], Theta1))
    my_q_.append(make_q([1, 0, 0], Theta2))
    my_q_.append(make_q([0, 0, 1], Theta3_))
    my_q_.append(make_q([1, 0, 0], Theta4_))

    my_Q_ = []
    my_Q_.append(my_cross(my_q_[0], my_q_[1]))
    my_Q_.append(my_cross(my_Q_[0], my_q_[2]))
    my_Q_.append(my_cross(my_Q_[1], my_q_[3]))
    my_Q_.append(my_cross(my_Q_[2], my_q_[4]))

    qx04 = my_Q_[3][0]
    qy04 = my_Q_[3][1]
    qz04 = my_Q_[3][2]
    qw04 = my_Q_[3][3]
    qx5 = q[0]
    qy5 = q[1]
    qz5 = q[2]
    qw5 = q[3]

    C5_ = (qx04*qx5 + qy04*qy5)/(qx04**2 + qy04**2)
    S5_ = (qx5*qy04 - qy5*qx04)/(qx04**2 + qy04**2)
    Theta5_ = 2*math.atan2(S5_, C5_)

    js = fixPi([Theta0, Theta1, Theta2, Theta3_, Theta4_, Theta5_])
    return js

4.9. テスト

　さて、プログラムが完成したので実際に実行して計算が合っているのかの確認をしてみます。
まずは順運動学の式から、逆運動学の式に入れる手先位置・姿勢を生成します。

#ランダム関節角度random_jsを生成
random_js = []
random_js.append(random.uniform(-math.pi*17/18, math.pi*17/18))
random_js.append(random.uniform(-math.pi*100/180, math.pi*135/180))
random_js.append(random.uniform(-math.pi*12/18, math.pi*153/180))
random_js.append(random.uniform(-math.pi*27/18, math.pi*27/18))
random_js.append(random.uniform(-math.pi*12/18, math.pi*12/18))
random_js.append(random.uniform(-math.pi*36/18, math.pi*36/18))
random_js = fixPi(js)

#random_jsから、手先座標[x, y, z], 姿勢qtnを導出
L = [0.1975, 0.1975, 0.340, 0.197, 0.143, 0.070, 0.035]
TTs = FK(L, random_js)
qtn = check_q(random_js)
x = TTs[6][0, 3]
y = TTs[6][1, 3]
z = TTs[6][2, 3]

これで得られた手先座標・姿勢を、逆運動学の関数 AnalyticSolution() に入力することで、逆運動学の解が得られます。
ここで、同じ手先位置・姿勢を取ることができる関節角度が複数パターンあることに注意が必要です。例えば、 2. のときに図で示したような山形の姿勢と谷形の姿勢では同じ手先位置・姿勢になります。

▼同じ手先位置・姿勢で異なる関節角度を取る例

そのため、逆運動学の解の $js$ と正解データの $js$ が必ずしも一致するとは限りません。
逆運動学の計算が合っているかどうかを確認するためには、逆運動学から求まった $js$ で順運動学を解き、その結果出た手先位置・姿勢が入力値と一致しているかどうかを確かめれば良いです。

#逆運動学で各関節角度calc_jsを求める
calc_js = AnalyticSolution(x, y, z, qtn)

#calc_jsから、手先座標[calc_x, calc_y, calc_z], 姿勢calc_qtnを導出
calc_TTs = FK(L, calc_js)
calc_qtn = check_q(calc_js)
calc_x = calc_TTs[6][0, 3]
calc_y = calc_TTs[6][1, 3]
calc_z = calc_TTs[6][2, 3]

正解データと逆運動学から得たデータを比較してみます。

print("     xyz:", [x, y, z])
print("calc_xyz:", [calc_x, calc_y, calc_z])

print("      Quaternion:", qtn)
print(" calc_Quaternion:", calc_qtn)

▼実行結果

このように、幾何解法による逆運動学で正確な解を得ることができました。
基本的には関節可動域の範囲での逆運動学は解くことができますが、今回はアームが山形のアーチ状に姿勢を取ることと、手先位置の方向に対してアームが正面を向くことを前提に逆運動学を解いているので、それ以外の状況でしか取ることができない手先位置・姿勢の解は求められません。
とはいえ、それ以外の状況となると「アームが一回転する状況」や「手先位置がロボットアームの内部にめり込んでいる状況」ということになるので、基本的には問題なく逆運動学の解が求まります。

5. Pybulletでのシミュレーション

5.0. 方針

　最後に、今回求めた逆運動学の計算プログラムを用いてロボットアームをシミュレーション環境で動かしてみます。

このシミュレーションでは、せっかくクォータニオンを用いた逆運動学の解を出したので

目標位置・姿勢をランダムに指定
目標姿勢はクォータニオンで指定
指定された手先位置・姿勢を取るようにロボットアームを動かす

といった方針でやっていきます。

ロボットアームの目標位置には、姿勢を可視化しやすいようにxyz軸を模した物体を置きます。

▼xyz軸を模した目標物体

5.1. 実行コード

このコードを動かすためには、pybullet環境の構築とplane.urdf、axis_s.urdf、vs_068.urdfの３つが必要です。

Pybullet環境の構築についてはこちらの記事を参考にして下さい。

URDFを利用したいという方は以下をクリックしてコードをコピペして下さい。

plane.urdf (**クリックして表示**)

plane.urdf

<?xml version="1.0" ?>
<robot name="plane">
  <link name="planeLink">
  <contact>
      <lateral_friction value="1"/>
  </contact>
  <inertial>
    <origin rpy="0 0 0" xyz="0 0 0"/>
    <mass value=".0"/>
    <inertia ixx="0" ixy="0" ixz="0" iyy="0" iyz="0" izz="0"/>
  </inertial>
  <visual>
    <origin rpy="0 0 0" xyz="0 0 -0.5"/>
    <geometry>
      <box size="10 10 1"/>
    </geometry>
    <material name="Gray">
      <color rgba="0.8 0.8 0.8 1" />
    </material>
  </visual>
  <collision>
    <origin rpy="0 0 0" xyz="0 0 -0.5"/>
    <geometry>
    <box size="10 10 1"/>
    </geometry>
  </collision>
  </link>
</robot>

axis_s.urdf (**クリックして表示**)

```:axis_s.urdf ```

vs_068.urdf (**クリックして表示**)

vs_068.urdf

<?xml version="1.0"?>
<robot name="vs-068">
  <link name="base">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0 0 0" />
      <mass value = "0.0001" />
      <inertia ixx = "0.0001" ixy = "0" ixz = "0" iyy = "0.0001" iyz = "0" izz = "0.0001" />
    </inertial>
  </link>
  <link name="stand">
    <contact>
      <lateral_friction value = "100" />
    </contact>
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.09875" />
        <mass value = "5000" />
        <inertia ixx = "54.5" ixy = "0" ixz = "0" iyy = "54.5" iyz = "0" izz = "76.6" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.09875"/>
      <geometry>
        <cylinder radius="0.175" length="0.1975"/>
      </geometry>
      <material name="Gray">
        <color rgba="0.8 0.8 0.8 1" />
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.09875" />
      <geometry>
        <cylinder radius="0.175" length="0.1975"/>
      </geometry>
    </collision>
  </link>
  <joint name="base_stand" type="fixed" >
    <parent link = "base" />
    <child link = "stand" />
    <origin rpy = "0 0 0" xyz = "0.000 0.000 0.000" />
  </joint>
  <link name="arm1">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 -0.015 0.12875" />
        <mass value = "7.5" />
        <inertia ixx = "0.066441" ixy = "0" ixz = "0" iyy = "0.075957" iyz = "0" izz = "0.059516" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 -0.015 0.12875"/>
      <geometry>
        <box size="0.235 0.20 0.2575"/>
      </geometry>
      <material name="Gray">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 -0.015 0.12875" />
      <geometry>
        <box size = "0.235 0.20 0.2575" />
      </geometry>
    </collision>
  </link>
  <joint name="stand_arm1" type="revolute" >
    <parent link = "stand" />
    <child link = "arm1" />
    <origin rpt = "0 0 0" xyz = "0 0 0.1975" />
    <axis xyz = "0 0 1" />
    <limit effort="10000.0" lower="-2.96705972839036" upper="2.96705972839036" velocity="3.15"/>
  </joint>
  <link name="arm2">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.17" />
        <mass value = "10" />
        <inertia ixx = "0.17333" ixy = "0" ixz = "0" iyy = "0.18008" iyz = "0" izz = "0.03075" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.17"/>
      <geometry>
        <box size="0.15 0.120 0.44"/>
      </geometry>
      <material name="Gray">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.17" />
      <geometry>
        <box size = "0.15 0.120 0.44" />
      </geometry>
    </collision>
  </link>
  <joint name="arm1_arm2" type="revolute" >
    <parent link = "arm1" />
    <child link = "arm2" />
    <origin rpy = "0 0 0" xyz = "0.000 -0.03 0.1975" />
    <limit effort="10000.0" lower="-1.7453292519943295" upper="2.356194490192345" velocity="3.15"/>
  </joint>
  <link name="arm3">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.0735" />
        <mass value = "7.5" />
        <inertia ixx = "0.044381" ixy = "0" ixz = "0" iyy = "0.044381" iyz = "0" izz = "0.01250" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.0735"/>
      <geometry>
        <box size="0.1 0.1 0.247"/>
      </geometry>
      <material name="Gray">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.197" />
      <geometry>
        <box size = "0.1 0.1 0.247" />
      </geometry>
    </collision>
  </link>
  <joint name="arm2_arm3" type="revolute" >
    <parent link = "arm2" />
    <child link = "arm3" />
    <origin rpy = "1.5707963267948966 0 0" xyz = "0.000 0.000 0.34" />
    <limit effort="10000.0" lower="-3.6651914291880923" upper="1.0995574287564276" velocity="3.15"/>
  </joint>
  <link name="arm4">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.080" />
        <mass value = "5" />
        <inertia ixx = "0.014833" ixy = "0" ixz = "0" iyy = "0.014833" iyz = "0" izz = "0.0083333" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.080"/>
      <geometry>
        <box size="0.1 0.1 0.160"/>
      </geometry>
      <material name="Gray">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.08" />
      <geometry>
        <box size = "0.10 0.10 0.16" />
      </geometry>
    </collision>
  </link>
  <joint name="arm3_arm4" type="revolute" >
    <parent link = "arm3" />
    <child link = "arm4" />
    <axis xyz="0 0 1"/>
    <origin rpy = "0 0 0" xyz = "0.000 0.000 0.197" />
    <limit effort="10000.0" lower="-4.71238898038469" upper="4.71238898038469" velocity="3.15"/>
  </joint>
  <link name="arm5">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.03" />
        <mass value = "2.5" />
        <inertia ixx = "0.0020833" ixy = "0" ixz = "0" iyy = "0.0015208" iyz = "0" izz = "0.00093750" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.03"/>
      <geometry>
        <box size="0.03 0.06 0.08"/>
      </geometry>
      <material name="Black">
        <color rgba="0.3 0.3 0.3 1" />
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.03" />
      <geometry>
        <box size = "0.03 0.06 0.08" />
      </geometry>
    </collision>
  </link>
  <joint name="arm4_arm5" type="revolute" >
    <parent link = "arm4" />
    <child link = "arm5" />
    <origin rpy = "0 0 0" xyz = "0.000 0.000 0.143" />
    <limit effort="10000.0" lower="-2.0943951023931953" upper="2.0943951023931953" velocity="3.15"/>
  </joint>
  <link name="arm6">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.005" />
        <mass value = "0.5" />
        <inertia ixx = "0.000032292" ixy = "0" ixz = "0" iyy = "0.000032292" iyz = "0" izz = "0.00005625" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.005"/>
      <geometry>
        <cylinder radius="0.015" length="0.01"/>
      </geometry>
      <material name="Black">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz="0 0 0.005"/>
      <geometry>
        <cylinder radius="0.015" length="0.01"/>
      </geometry>
    </collision>
  </link>
  <joint name="arm5_arm6" type="revolute" >
    <parent link = "arm5" />
    <child link = "arm6" />
    <origin rpy = "0 0 0" xyz = "0.000 0.000 0.07" />
    <axis xyz="0 0 1"/>
    <limit effort="10000.0" lower="-3.141592653589793" upper="3.141592653589793" velocity="3.15"/>
  </joint>
  <link name="gripper1">
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.005" />
        <mass value = "0.020" />
        <inertia ixx = "0.01" ixy = "0" ixz = "0" iyy = "0.01" iyz = "0" izz = "0.01" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.005"/>
      <geometry>
        <box size="0.04 0.01 0.01"/>
      </geometry>
      <material name="Black">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.005" />
      <geometry>
        <box size = "0.04 0.01 0.010" />
      </geometry>
    </collision>
  </link>
  <joint name="arm6_gripper1" type="fixed" >
    <parent link = "arm6" />
    <child link = "gripper1" />
    <origin rpy = "0 0 0" xyz = "0.000 0.000 0.010" />
  </joint>
  <link name="gripper2">
    <contact>
      <lateral_friction value = "10" />
    </contact>
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.0075" />
        <mass value = "0.003" />
        <inertia ixx = "0.01" ixy = "0" ixz = "0" iyy = "0.005" iyz = "0" izz = "0.005" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.0075"/>
      <geometry>
        <box size="0.005 0.01 0.015"/>
      </geometry>
      <material name="Black">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.0075" />
      <geometry>
        <box size = "0.005 0.010 0.015" />
      </geometry>
    </collision>
  </link>
  <joint name="gripper1_gripper2" type="prismatic" >
    <parent link = "gripper1" />
    <child link = "gripper2" />
    <origin rpy = "0 0 0" xyz = "-0.0175 0.000 0.01" />
    <limit effort="10000.0" lower="0" upper="0.015" velocity="0.5"/>
  </joint>
  <link name="gripper3">
    <contact>
      <lateral_friction value = "10" />
    </contact>
    <inertial>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.0075" />
        <mass value = "0.003" />
        <inertia ixx = "0.01" ixy = "0" ixz = "0" iyy = "0.005" iyz = "0" izz = "0.005" />
    </inertial>
    <visual>
      <origin rpy="0 0 0" xyz="0 0 0.0075"/>
      <geometry>
        <box size="0.005 0.01 0.015"/>
      </geometry>
      <material name="Black">
      </material>
    </visual>
    <collision>
      <origin rpy = "0 0 0" xyz = "0.000 0.000 0.0075" />
      <geometry>
        <box size = "0.005 0.010 0.015" />
      </geometry>
    </collision>
  </link>
  <joint name="gripper1_gripper3" type="prismatic" >
    <parent link = "gripper1" />
    <child link = "gripper3" />
    <origin rpy = "0 0 0" xyz = "0.0175 0.000 0.01" />
    <limit effort="10000.0" lower="-0.015" upper="0" velocity="0.5"/>
  </joint>
</robot>

pybullet_arm_simulation.py

import pybullet as p
import time
import math
import numpy as np
import random
import qiita_AnalyticSolution as AS

#P制御の関数
def P_control(K, theta, js):
  dtheta = theta - js
  if dtheta > 0.0001 or -0.0001 > dtheta:
    return K*dtheta
  else:
    return 0

phisicsClient = p.connect(p.GUI)

#物体の位置[x,y,z]をランダムに決定
random_js = []
random_js.append(random.uniform(-math.pi*17/18, math.pi*17/18))
random_js.append(random.uniform(-math.pi*100/180, math.pi*135/180))
random_js.append(random.uniform(-math.pi*12/18, math.pi*153/180))
random_js.append(random.uniform(-math.pi*27/18, math.pi*27/18))
random_js.append(random.uniform(-math.pi*12/18, math.pi*12/18))
random_js.append(random.uniform(-math.pi*36/18, math.pi*36/18))

L = [0.1975, 0.1975, 0.340, 0.197, 0.143, 0.070, 0.035] #アームの長さ

xyz = AS.FK(L, random_js)
x = xyz[6][0, 3]
y = xyz[6][1, 3]
z = xyz[6][2, 3]
quaternion = AS.check_q(random_js)

K=[0.1, 0.1, 0.1, 0.1, 0.1, 0.1] #P制御のゲイン

#URDF読み込み
p.loadURDF("plane.urdf", basePosition = [0, 0, 0])
p.loadURDF("axis_s.urdf", basePosition = [x, y, z], baseOrientation=quaternion)
obUids = p.loadURDF("vs_068.urdf", basePosition = [0, 0, 0])

robot = obUids

gravId = p.addUserDebugParameter("gravity", -10, 10, -10)
jointIds = []
paramIds = []

p.setPhysicsEngineParameter(numSolverIterations = 10)
p.changeDynamics(robot, -1, linearDamping = 0, angularDamping = 0)

#Joint読み込み
for j in range(p.getNumJoints(robot)):
  p.changeDynamics(robot, j, linearDamping = 0, angularDamping = 0)
  info = p.getJointInfo(robot, j)
  #print(info)
  jointName = info[1]
  jointType = info[2]
  if (jointType == p.JOINT_PRISMATIC or jointType == p.JOINT_REVOLUTE):
    jointIds.append(j)
    if j < 7:
      paramIds.append(p.addUserDebugParameter(jointName.decode("utf-8"), -4, 4, 0))
    else:
      paramIds.append(p.addUserDebugParameter(jointName.decode("utf-8"), 0, 0.015, 0))

#各関節角を設定
targetPos = [0 for i in range(len(paramIds))]

#逆運動学を解いて目標関節角を得る
goalTheta = AS.AnalyticSolution(x, y, z, quaternion)

#シミュレーションの開始
p.setRealTimeSimulation(1)
while (1):
  p.setGravity(0, 0, p.readUserDebugParameter(gravId))
  for i in range(len(paramIds)):
    c = paramIds[i]
    p.setJointMotorControl2(robot, jointIds[i], p.POSITION_CONTROL, targetPos[i], force=5 * 240.)

  #P制御
  for i in range(6):
    if i != 2:
      targetPos[i] += P_control(K[i], goalTheta[i], targetPos[i])
    else:
      targetPos[i] += P_control(K[i], goalTheta[i] - math.pi/2, targetPos[i])

  #print(targetPos)
  time.sleep(0.05)

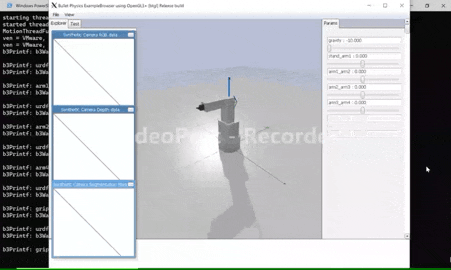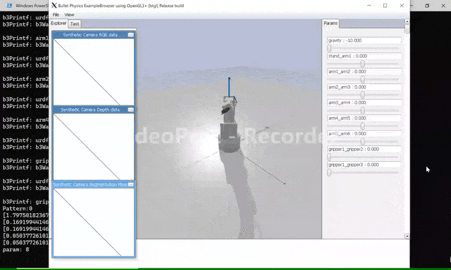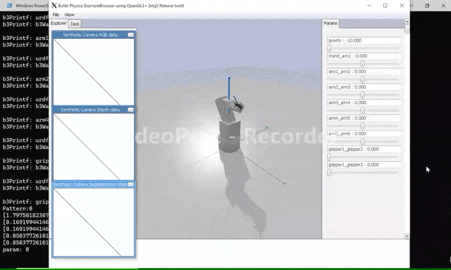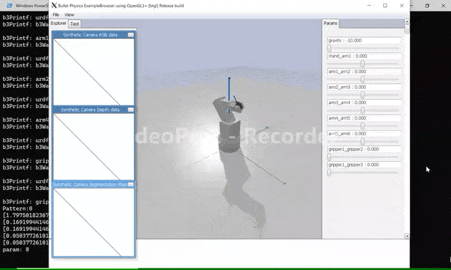
5.2. 実行結果

▼実行結果例

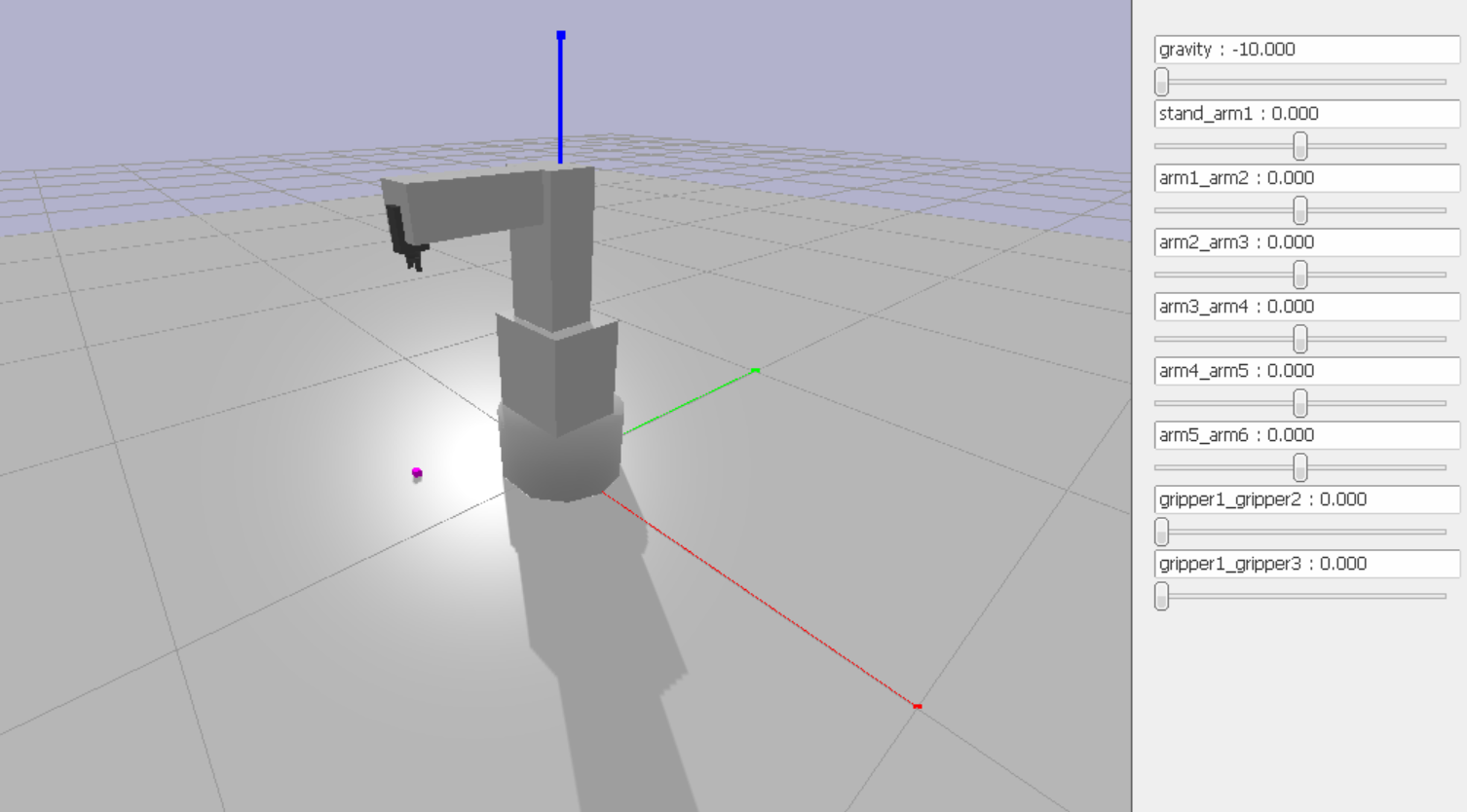
上画像のように、綺麗に目標物体に到達していることが分かります。

▼実行結果例 (GIF)

アームが滑らかに動作しているのが分かります。

6. 最後に

今回は6自由度のロボットアームの逆運動学を幾何解法で解きましたが、他のロボットアームであっても今回解説した方法と同じような方針で解くことができると思います。
基本的にはクォータニオンなどの姿勢と、余弦定理、空間ベクトルといった幾何的な情報を用いれば、他の6自由度アームの逆運動学も解けるでしょう。
分かりずらい部分もあったかと思いますが、この記事が少しでも皆さまの参考になれば幸いです。

　また、この記事は早稲田大学尾形研究室での活動の一環として書いています。
ロボットや深層学習について研究しているので、興味のある方は以下の研究室HPをご覧下さい。

尾形哲也研究室

【逆運動学】6自由度ロボットアームの解析解法(幾何解法)

目次