Pybulletでロボットを動かす
ロボットアームを自由に動かすためには順運動学と逆運動学が必要です。
この記事では逆運動学の数値解法についての解説と、Pybulletでの実装方法を載せています。
順運動学については前回の記事で解説しているので、順運動学について知りたい方はこちらを参考にして下さい。
動作環境
-
Windows10
-
WSL2
-
Ubunu18.04
逆運動学
逆運動学とは
ロボットアームにおける逆運動学とは、ある位置まである姿勢で手先アームを到達させるための適切な関節角度を求めることを指します。
例えば「机の上のペンを取る」という動作をするには、ペンの位置を把握して、腕の関節角を調整することでペンの位置まで手を移動させる必要があります。
つまり、私たちはペンを掴むという動作をするとき、手がペンに届くようなちょうどいい関節角度を毎回見つけているという風に捉えることができます。
これがまさに逆運動学でやっていることです。
逆運動学の解法
逆運動学の解法は解析解法と数値解法の2種類に分かれます。
解析解法
解析解法は、順運動学の数式を変形することで逆運動学の数式を導出する手法です。
解析解法のメリットは、数式が求まってさえしまえば常に正確な解を得られることです。2自由度アームなどの簡単に解析解が求まるアームを扱うときには解析解法が役に立ちます。
しかしデメリットとして、6自由度アームなどの自由度の高いアームになると解の導出がとても困難であったり、導出できたとしてもかなり面倒だったりします。
数値解法
数値解法は、目標位置に近づくような関節角の微小変化を逐一計算することで、少しずつ目標位置と現在位置の差を埋めていく手法です。
数値解法のメリットは、6自由度アームなどの複雑なアームでも解を得ることができることです。
しかしデメリットとして、求解に時間がかかることや、目標位置と誤差が生まれてしまうことが挙げられます。
今回は6自由度アームの逆運動学を求めていくので、数値解法を採用します。
数値解法
数値解法の具体的な説明については省略しますが、詳細はこちらの記事が参考になるかと思います。
数値解法にはいくつかの手法があります。
例えば上記の記事で紹介されているものでは最急降下法、Newton-Raphson法、Gauss-Newton法、Levenberg-Marquardt法、可変計量法、共役勾配法などがあります。
今回はその中でも、再急降下法による逆運動学の数値解法を解説します。
要は、順運動学の式を微小区間において線形近似することで逆運動学の式に変形するという方法です。
アームの手先座標・姿勢をA, そのときのアームの各関節角をΘとする.\\
A = [x, y, z, φ, θ, ψ]\\
Θ=[θ_1,θ_2, ・・・, θ_n]\\
順運動学の式は\\
f(Θ) = A \\
と表せる.\
この順運動学の式を微分して線形関数に近似させると次式のようになる.\\
J \dot Θ = \dot A\\
(このJのことをヤコビ行列と言います.)\\
式変形すると\\
\dot Θ = J^{-1} \dot A\\
ヤコビ行列 $J$ の逆行列 $J^{-1}$ が求まれば、数値解法によって関節角を微小変化させ続けることで最終的に目標位置・姿勢に到達できます。
逆運動学のプログラムを実装
使用するロボットアームの選択
逆運動学を解く前に、まずは使用するロボットアームを決めなくてはいけません。
前回の記事で作成したVS-068というロボットアームを使用することにします。
このアームの寸法、関節可動域については前回の記事を参照して下さい。
逆運動学のPythonコード
import numpy as np
import math
def fixPi(Js):
js=Js
for j in range(len(Js)):
if js[j]>math.pi:
js[j]=js[j]-int((js[j]+math.pi)/(2*math.pi))*2*math.pi
elif js[j]<-math.pi:
js[j]=js[j]-int((js[j]-math.pi)/(2*math.pi))*2*math.pi
return js
def forwardKinematicsThreeJoints3D(L, js):
Ts = []
c0 = math.cos(js[0])
s0 = math.sin(js[0])
c1 = math.cos(js[1])
s1 = math.sin(js[1])
c2 = math.cos(js[2])
s2 = math.sin(js[2])
c3 = math.cos(js[3])
s3 = math.sin(js[3])
c4 = math.cos(js[4])
s4 = math.sin(js[4])
c5 = math.cos(js[5])
s5 = math.sin(js[5])
Ts.append(np.matrix([[c0, -s0, 0, 0], [s0, c0, 0, 0], [0, 0, 1, L[0]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[1, 0, 0, 0], [0, c1, -s1, -0.03], [0, s1, c1, L[1]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[1, 0, 0, 0], [0, c2, -s2, 0], [0, s2, c2, L[2]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[c3, -s3, 0, 0], [s3, c3, 0, 0], [0, 0, 1, L[3]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[1, 0, 0, 0], [0, c4, -s4, 0], [0, s4, c4, L[4]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[c5, -s5, 0, 0], [s5, c5, 0, 0], [0, 0, 1, L[5]], [0, 0, 0, 1]]))
Ts.append(np.matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, L[6]], [0, 0, 0, 1]]))
TTs = Ts[0]*Ts[1]*Ts[2]*Ts[3]*Ts[4]*Ts[5]*Ts[6]
return TTs
def getxyz(L,js):
TTs=forwardKinematicsThreeJoints3D(L, js)
return [TTs[0,3],TTs[1,3],TTs[2,3]]
def getOrientation(L,js):
ZXZ=forwardKinematicsThreeJoints3D(L, js)
theta = math.atan2(math.sqrt(ZXZ[2,0]**2+ZXZ[2,1]**2),ZXZ[2,2])
if abs(math.sin(theta))==0:
theta=0
phi=0
psy=math.atan2(-ZXZ[0,1],ZXZ[0,0])
else:
phi=math.atan2(ZXZ[0,2],-ZXZ[1,2])
psy=math.atan2(ZXZ[2,0],ZXZ[2,1])
if abs(math.sin(phi))==0:
phi=0
if abs(math.sin(psy))==0:
psy=0
#print("js:",js)
#print("orientaton:",fixPi([phi,theta,psy]))
return fixPi([phi,theta,psy])
def getDifferential(L,js):
d=10e-4
vfx=[]
djs=[js[i] for i in range(len(js))]
for i in range(len(js)):
djs[i]+=d
vfx.append(fixPi((np.array(getOrientation(L,djs))-np.array(getOrientation(L,js)))/d))
djs[i]-=d
return vfx
# print("vfx:",getDifferential(L,js))
def move_P(K, theta, js):
dtheta = theta-js
if dtheta>0.0001 or -0.0001>dtheta:
return K*dtheta
else:
return 0
def calcJointVelocity(L, vx, vy, vz, vtheta, js):
#print(js)
L0=L[0]
L1=L[1]
L2=L[2]
L3=L[3]
L4=L[4]
L5=L[5]
L6=L[6]
c0 = math.cos(js[0])
s0 = math.sin(js[0])
c1 = math.cos(js[1])
s1 = math.sin(js[1])
c12 = math.cos(js[1]+js[2])
s12 = math.sin(js[1]+js[2])
c3 = math.cos(js[3])
s3 = math.sin(js[3])
c4 = math.cos(js[4])
s4 = math.sin(js[4])
c5 = math.cos(js[5])
s5 = math.sin(js[5])
D = getDifferential(L,js)
""" 目標手先位置Vx, Vy, Vthetaと現在関節角度jsを使う """
J = np.matrix([
[c0*(s1*L2+s12*L3+s12*L4)+(L5+L6)*(-s0*s3*s4+c0*c12*c3*s4+c0*s12*c4),
s0*(c1*L2+c12*L3+c12*L4)+(L5+L6)*(-s0*s12*c3*s4+s0*c12*c4),
s0*(c12*L3+c12*L4)+(L5+L6)*(-s0*s12*c3*s4+s0*c12*c4),
(L5+L6)*(c0*s3*c4+s0*c12*c3*c4-s0*s12*s4),
],
[s0*(s1*L2+s12*L3+s12*L4)+(L5+L6)*(c0*s3*s4+s0*c12*c3*s4+s0*s12*c4),
-c0*(c1*L2+c12*L3+c12*L4)+(L5+L6)*(c0*s12*c3*s4-c0*c12*c4),
-c0*(c12*L3+c12*L4)+(L5+L6)*(c0*s12*c3*s4-c0*c12*c4),
(L5+L6)*(s0*s3*c4-c0*c12*c3*c4+c0*s12*s4),
],
[0,
-s1*L2-s12*L3-s12*L4+(L5+L6)*(-c12*c3*s4-s12*c4),
-s12*L3-s12*L4+(L5+L6)*(-c12*c3*s4-s12*c4),
(L5+L6)*(-s12*c3*c4-c12*s4),
],
[D[0][1], D[1][1], D[2][1], D[4][1]],
])
#print("J:",J.shape)
#print(J)
J_ = np.linalg.pinv(J)
vjs = J_ * np.array([[vx], [vy], [vz], [vtheta]])
#print (vjs)
return vjs
def inverseKinematicsThreeJoints3D(L, x, y, z, theta, JS):
dx=0.01
dy=0.01
dz=0.01
dtheta=0.01
js=JS
i=0
while(True):
print("####",i,"####")
TTs = forwardKinematicsThreeJoints3D(L, js)
ax = TTs[0,3]
ay = TTs[1,3]
az = TTs[2,3]
ZXZ = getOrientation(L,js)
atheta= ZXZ[1]
print(ax,ay,az,atheta)
vx=x-ax
vy=y-ay
vz=z-az
vtheta=theta-atheta
#print(vtheta)
if math.sqrt(vx**2+vy**2+vz**2)<0.001 and abs(vtheta)<0.01:
print("解が収束しました")
break
if i==1000:
print("解が収束しませんでした。")
break
dx=0.01 if vx>=0.01 else -0.01 if vx<=-0.01 else vx
dy=0.01 if vy>=0.01 else -0.01 if vy<=-0.01 else vy
dz=0.01 if vz>=0.01 else -0.01 if vz<=-0.01 else vz
dtheta=0.01 if vtheta>=0.01 else -0.01 if vtheta<=-0.01 else vtheta
#print(dx,dy,dz,dtheta)
vjs=calcJointVelocity(L, dx, dy, dz, dtheta, js)
#print(vjs)
js[0]+=float(vjs[0])
js[1]+=float(vjs[1])
js[2]+=float(vjs[2])
js[3]=0
js[4]+=float(vjs[3])
js[5]=0
i+=1
for j in range(len(js)):
if js[j]>math.pi:
js[j]=js[j]-int((js[j]+math.pi)/(2*math.pi))*2*math.pi
elif js[j]<-math.pi:
js[j]=js[j]-int((js[j]-math.pi)/(2*math.pi))*2*math.pi
return js
各関数の説明
| 関数 | 入力値 | 出力値 | 説明 |
|---|---|---|---|
| fixPi(Js) | 逆運動学を解いて求まった各関節角度 | 角度の範囲を$[-π, π]$に直した各関節角度 | 逆運動学を解いて出た値は$[-π, π]$に収まっていないため、角度を直すための関数 |
| forwardKinematicsThreeJoints3D(L, js) | アームの長さLと各関節角js | 同時座標変換行列TTs | 順運動学を解いて同時座標変換行列を導出する関数 |
| getxyz(L,js) | アームの長さLと各関節角js | 手先座標[x, y, z] | 同時座標変換行列から手先座標を求める関数 |
| getOrientation(L,js) | アームの長さLと各関節角js | オイラー角(ZXZ軸) | 同時座標変換行列から手先姿勢を求める関数 |
| getDifferential(L,js) | アームの長さLと各関節角js | オイラー角の微分値(ZXZ軸) | ヤコビ行列をつくるための微分関数 |
| move_P(K, theta, js) | P制御のゲインKと目標関節角thetaと各関節角js | 各関節角の変化量 | P制御を行う関数 |
| calcJointVelocity(L, vx, vy, vz, vtheta, js) | アームの長さLとX,Y,Z軸方向への移動変化量と各関節角js | vx,vy,vzだけ移動するのに必要な各関節角の変化量 | 数値解法のための関数 |
| inverseKinematicsThreeJoints3D(L, x, y, z, theta, JS) | アームの長さLと目的座標[x,y,z]と目的姿勢thetaと初期関節角度JS | 目的座標・姿勢になるための各関節角 | 逆運動学を解くメインの関数 |
先に数式で示したように、逆運動学を解く流れは
①順運動学の式を立てる
②順運動学の式を各関節角度で微分してヤコビ行列を得る
③ヤコビ行列の逆行列を取る
④逆行列と手先位置と手先姿勢の微小変化量から各関節角の微小変化量を求める
というアルゴリズムの繰り返しになっています。
このアルゴリズムをプログラムにすると
①の関数がforwardKinematicsThreeJoints3D(L, js)、
②と③の関数がcalcJointVelocity(L, vx, vy, vz, vtheta, js)、
④の関数がinverseKinematicsThreeJoints3D(L, x, y, z, theta, JS)
となります。
②でヤコビ行列の手先姿勢部分を得るためにgetDifferential(L,js)で微分しています。
①~④のアルゴリズムを繰り返して出た逆運動学の解は、範囲が[-π,π]に収まっていないため、関節角の可動域外の解になってしまうことがあるので、fixPi(Js)という関数で角度を[-π,π]の範囲に直しています。
実行結果
試しに、手先位置[x, y, z] = [0.3, 0.3, 0.3]、手先姿勢90°となるような各関節角度を逆運動学で求めてみます。
L=[0.1975,0.1975,0.340,0.197,0.143,0.070,0.010]
js=[math.pi/2,math.pi/2,0,0,0,0]
Js=inverseKinematicsThreeJoints3D(L, 0.3, 0.3, 0.3, math.pi, js)
print(Js)
数値解法のアルゴリズムを157回繰り返した結果、無事に各関節角が求まりました。
157回目での手先位置、手先姿勢の値をみると誤差はとても小さく収まっています。
このコードの手先姿勢(オイラー角)について
オイラー角による手先姿勢の表現は通常、3回の軸回転で行います。
例えば上記のプログラムではZXZ軸回転によるオイラー角 $[φ, θ, ψ]$ で姿勢表現をしています。
詳細はこちらを参照して下さい
既にお気づきかもしれませんが、今回の逆運動学プログラムではX軸回転のθのみしか姿勢を求めていません。
これは手先姿勢よりも手先位置 $[x,y,z]$ の精度を重視したプログラムであるためです。
理論的には6自由度のロボットアームを使えば、関節の可動範囲内ではあらゆる手先位置、手先姿勢を取ることが可能ですが、その分、逆運動学を解くのが難しくなります。
そのため、今回のプログラムコードでは手先姿勢をθのみに絞ることで、逆運動学の解を求めやすくしています。
手先姿勢もしっかりと$[φ, θ, ψ]$で解きたい場合は、アームの初期状態を目的位置・姿勢に近い値にして解を求まりやすくするというような工夫をするという手があります。
また、そもそも今回用いたオイラー角での姿勢表現は、感覚的に理解しやすいため扱いやすいという反面、回転軸が揃うと自由度が3から2に下がってしまうジンバルロックという表現上の問題を抱えているため、それが解の収束性の悪さにつながることがあります。
そのため、オイラー角の代わりにクォータニオンという4元数を用いる方法があるので、気になった方はぜひ試してみると良いと思います。
クォータニオンについて詳しく知りたい方は、こちらの記事が非常に参考になると思います。
他にも位置と姿勢で優先順位を決めて、優先順位の低い方の誤差を最小にすることで逆運動学を解く優先度付き逆運動学という手法なども存在するそうです。
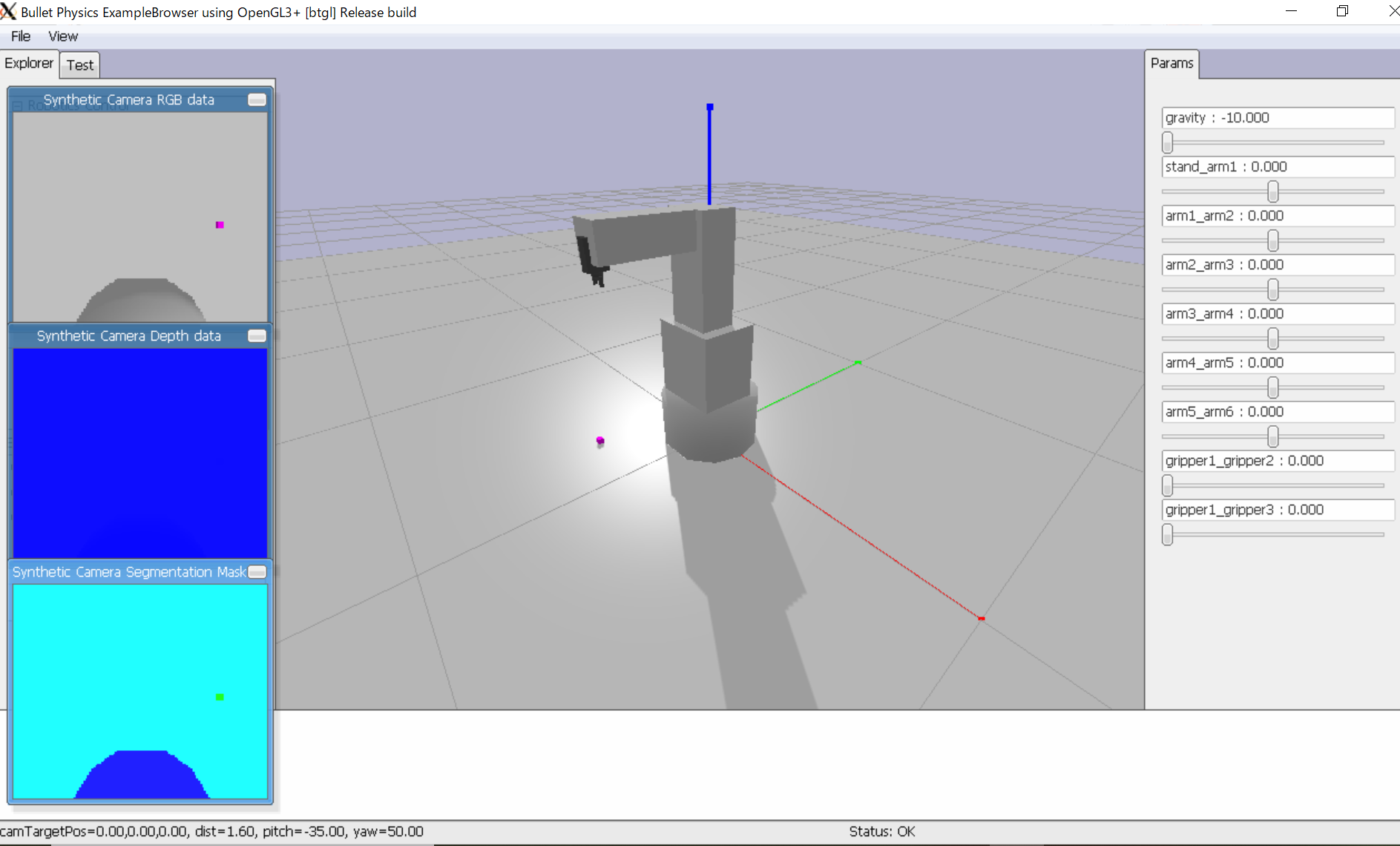
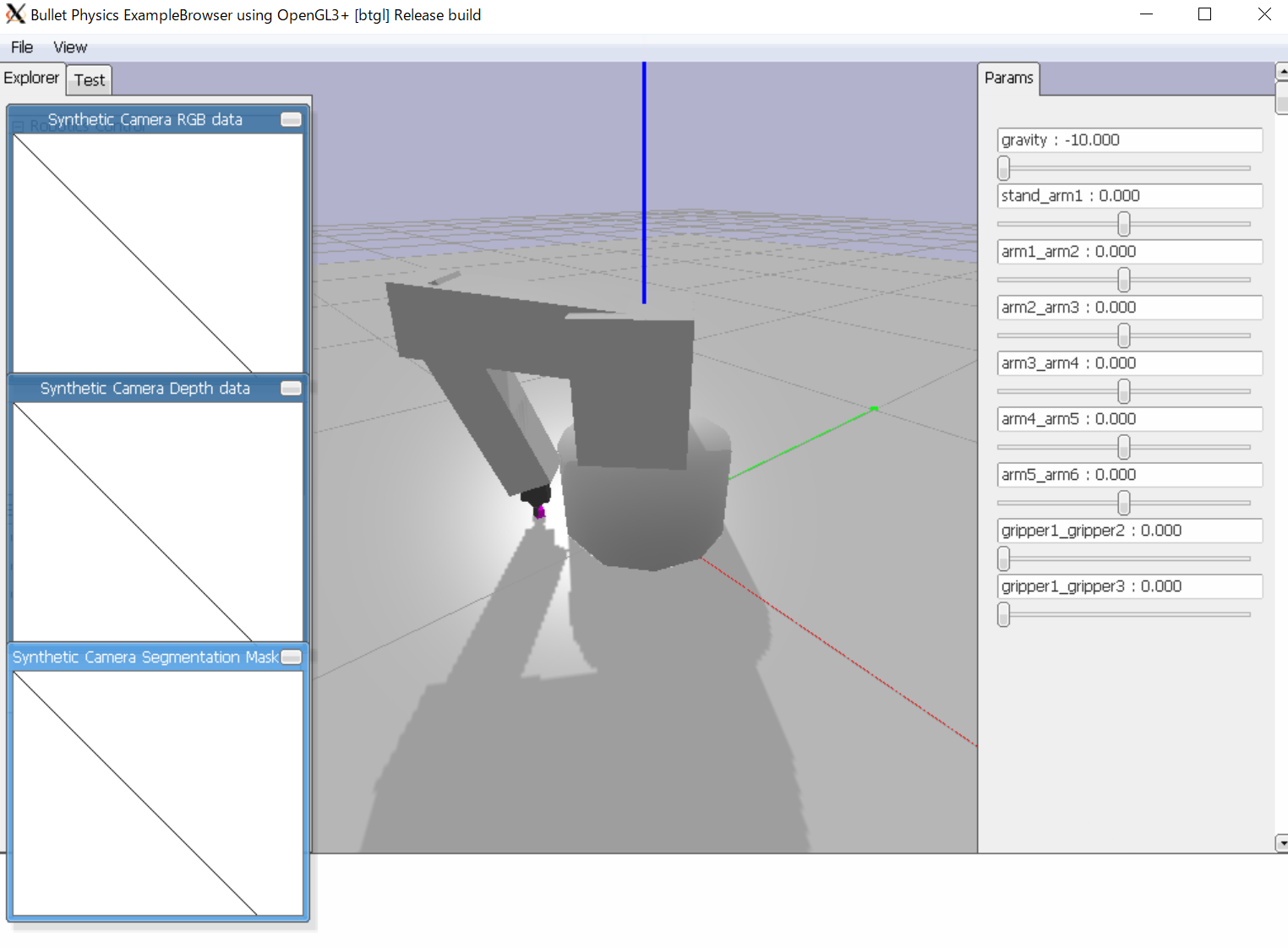
Pybulletで動作確認
Pybulletコード
逆運動学を解くことができたので、実際にPybulletでシミュレーションをしてみます。
import pybullet as p
import time
import math
import numpy as np
import random
import getPosition as ps
phisicsClient = p.connect(p.GUI)
# 物体の位置[x,y,z]をランダムに決定
random_r=random.uniform(0.2,0.5)
random_theta=random.uniform(-math.pi,math.pi)
x=random_r*math.cos(random_theta)
y=random_r*math.sin(random_theta)
z=0.01
L=[0.1975,0.1975,0.340,0.197,0.143,0.070,0.035] #アームの長さ
theta = math.pi #目標姿勢を90°に設定
K=[0.1,0.1,0.1,0.1,0.1] #P制御のゲイン
# URDF読み込み
p.loadURDF("plane.urdf", basePosition = [0, 0, 0])
p.loadURDF("box.urdf", basePosition = [x, y, z])
obUids = p.loadURDF("vs_068.urdf", basePosition = [0, 0, 0])
robot = obUids
gravId = p.addUserDebugParameter("gravity", -10, 10, -10)
jointIds = []
paramIds = []
p.setPhysicsEngineParameter(numSolverIterations=10)
p.changeDynamics(robot, -1, linearDamping=0, angularDamping=0)
# Joint読み込み
for j in range(p.getNumJoints(robot)):
p.changeDynamics(robot, j, linearDamping=0, angularDamping=0)
info = p.getJointInfo(robot, j)
#print(info)
jointName = info[1]
jointType = info[2]
if (jointType == p.JOINT_PRISMATIC or jointType == p.JOINT_REVOLUTE):
jointIds.append(j)
if j<7:
paramIds.append(p.addUserDebugParameter(jointName.decode("utf-8"), -4, 4, 0))
else:
paramIds.append(p.addUserDebugParameter(jointName.decode("utf-8"), 0, 0.015, 0))
# 各関節角を設定
targetPos=[0 for i in range(len(paramIds))]
# 逆運動学を解いて目標関節角を得る
goalTheta=ps.inverseKinematicsThreeJoints3D(L, x, y, z, math.pi, [0.1 for i in range(6)])
print(ps.getxyz(L, goalTheta))
print(goalTheta)
goalTheta2=[]
print("param:", len(paramIds))
# シミュレーションの開始
p.setRealTimeSimulation(1)
while (1):
p.setGravity(0, 0, p.readUserDebugParameter(gravId))
for i in range(len(paramIds)):
c = paramIds[i]
p.setJointMotorControl2(robot, jointIds[i], p.POSITION_CONTROL, targetPos[i], force=5 * 240.)
#P制御
for i in range(6):
if i!=2:
targetPos[i]+=ps.move_P(K[0], goalTheta[i], targetPos[i])
else:
targetPos[i]+=ps.move_P(K[0], goalTheta[i]-math.pi/2, targetPos[i])
#print(targetPos)
time.sleep(0.05)
実行結果
逆運動学を解くことで、紫色の目標物体までの関節角を求め、P制御によって物体までロボットアームを移動することに成功しています。
P制御や、PID制御について詳しく知りたい方はこちらの記事が参考になると思います。
最後に
この記事は早稲田大学の尾形研究室での活動の一環として書きました。
ロボットや深層学習について研究しているので、興味のある方は以下の研究室HPをご覧下さい。