統計学なかのt-testとp-valueの理解にかなり時間を使ってました.
t値とp値の計算の例をたまたま見つけたので,その流れをまとめます.
六年前にIT仕事の給料は$69873,今はIT仕事の給料は $69873ではないと仮設します.この仮設を証明したいです. ここでt-testとp-value($p$値)を利用して,証明することにします.
結論からいうと 求められたp値は 0.05より小さければ,仮設を証明できたことにします. p値は小さければ今のIT仕事の給料は$68873ではないという仮設の強い裏付けになります.
12人のITの仕事をやっている人のサンプルがすでにある状態で,
- このサンプル $n$ は12個
- この12人の平均給料 $\bar{x}$ は
$79180 - この12人給料サンプルの標準偏差 $s$ は
$14985 - 六年前のITの給料 $\mu_0$ は
$69873
上の4つのデータで$t$値と$p$値を求めることができます.
t=\frac{\bar{x} - \mu_0}{\frac{s}{\sqrt{n}}}
t=\frac{79180 - 69873}{\frac{14985}{\sqrt{12}}} = 2.15
$t$値は2.15であることが分かれば,p値の範囲もわかります.
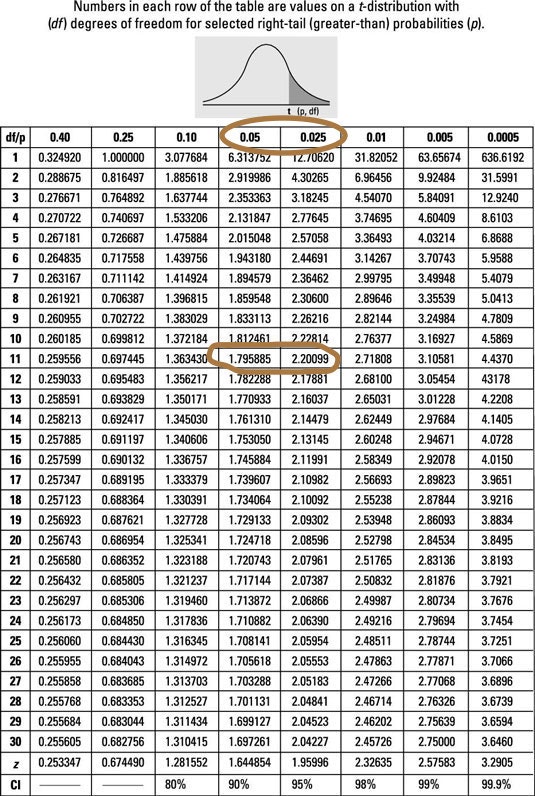
サンプルの数は12なので, degree of freedom(自由度)は n-1(11)です.
上の表を参照すると t値の2.15は 1.795885と2.20099の間にあるため,つまりp値は 0.05と0.025の間にあることがわかりました.
なので,求めたれたp値は 0.05より小さいので証明できました.