どうもーー!せるたわーθ改め(?)せるたわーしーぷです!!まずはContestantのみなさん、JOI二次予選おつかれさまでした!!!私は高2なので最初で最後のJOIとなりますが、全力を尽くせたので良かったと思います…!
さて、今回はJOI(日本情報オリンピック) 2022/2023二次予選のC問題「塗りつぶし (Painting)」の満点解法の解説をしていきます。方針は公式解説の小課題4,5に近いです。私はDFSを用いて実装しました。(ほかの方の提出をチラ見すると、みなさんUnion-Findを用いて解かれていますのでそちらのほうが簡単なのかもしれません…。w)
本稿では3パートに分けて、実装例も交えながらわかりやすくお話できるように努めました…が、わたしの力不足により長めの実装になってしまったので「この部分はもっとスマートにかけるぞ!!」という方は奮って軽くしていただけると嬉しいです!未来のJOIerに届け!!!
0.問題
どなたでも閲覧可能です。
1.考察
以下の①,②は自明なのですが、一応記述しておきます。下記「★」の部分から読んでいただいても問題ありません。少しばかり公式解説から引用させていただきます。
"色が異なる隣接するマスの境界で長方形を区切ると,長方形は何個かの部分に分かれます.これらの部分をいまからは「連結成分」と呼ぶことにしましょう."
(リンクを踏んで、小課題4のところを見ると同様の記述があります。)
①(クリックして展開)
いま、同じ連結成分内において、JOI君が異なるマスを選択したとしても、それらの指す領域は同じです。(例えば、入力例1の”マス(1,2)の領域”と”マス(2,1)の領域”は同じです。)②(クリックして展開)
同じ連結成分内においては、JOI君がどのマスを選んでも、彼が得点を最大化するためにとるべき行動は同じです。(例えば入力例1の場合、JOI君がマス(1,2),(2,1)のどちらを選んだとしても、マス(1,2)とマス(2,1)は同一の連結成分に属しますから、①より”マス(1,2)の領域”と”マス(2,1)の領域”は同じです。したがって、”マス(1,2)の領域”と”マス(2,1)の領域”のどちらについても、周囲の状況に鑑みると、色3で塗りつぶすのが最適だといえますね。)…というところまで私は競技中に考えたのですが、これらをどう実装してやればよいかがなかなか思いつかず、なにもできないままつらい1時間を過ごしました…笑
これまで書いたことのイメージはこんな感じ!右側のように持っていけたら勝ち!
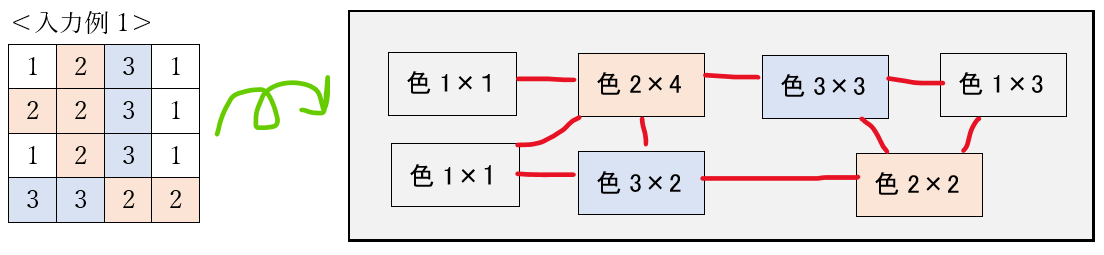
2.実装の方針
3パートに分けます!
Part1.「各連結成分の「色」と「マスの数」をDFSで取得!連結成分ごとに整理番号も割り振ろう!」
Part2.「各連結成分が、他の連結成分とどのようにつながっているかをこちらもDFSで記録する!」
Part3.「各連結成分について、隣接する連結成分の状況をみて、最善の行動をとると何点取れるかを決定する!」
3.実装たいむ!
Part.1「各連結成分の「色」と「マスの数」をDFSで取得!連結成分ごとに整理番号も割り振ろう!」
人間の目なら簡単ですが、コンピューターにやらせようとすると意外と行き詰まるのではないでしょうか…?(私は行き詰まりました)
とりあえず、下準備をしましょう!ざっくりどんな情報が必要かを考えます!
「色」はそのまま入力されたマス目を見ればよさそうですが、「マスの数」はどうしましょう…。私は、「現在注目中の連結成分のマスの数」を管理するint型変数をグローバル変数として宣言したうえで、DFS中に新しいマスに到着したときにそれをインクリメントしてゲットしました!(もちろん適切に初期化はしますよ…!)(もっと頭のいいやり方がありそうです。UFとか?なにもわかりませんが…。)
また、これより先で、どの連結成分に隣接しているかを調べる兼ね合いで、いちど各連結成分に整理番号を振らなければなりません…。これはDFSついでにできますね! ここでの整理番号は、連結成分を発見した順番とすればよいでしょう。ちょうどこの操作のような感じですね!(けんちょんさんの記事「DFS (深さ優先探索) 超入門! 〜 グラフ・アルゴリズムの世界への入口 〜【後編】」の該当部へのリンクです。けんちょんさんありがとうございます!!!)
さて、こうなると、各連結成分の整理番号をマスごとに保持する二次元配列が必要です。私はグローバル変数として宣言し、後でサイズを決めて(-1とかの、整理番号としてありえない数字で)初期化します。
また、帰ってきた結果をmap[整理番号]={色,マスの数}のような形式で記録する連想配列1が必要ですね!あ、そうそう、各連結成分の代表座標も連想配列1を用いて記録したほうがのちのち便利かもしれません…!ここで、「代表座標」は各連結成分において最初に発見されたマスの座標としましょう!
ここまで来たら準備完了!!実際にDFSをやっていきましょう!与えられた$ H×W $個のすべてのマスについて次の操作を行います;
いま、マス$ (i,j) $について考えているとすると、
- もし、すでに整理番号が割り当てられたマスならば、そこはスキップする。
- さもなくば、
- そのマスの色を調べる
- 連結成分中の全マスに整理番号を割り振るためのDFS(後述)を行う
- 帰ってきた結果を{色,マスの数}のpairのカタチで登録する
- 連結成分中の代表座標として$ (i,j) $をpairのカタチで登録する(後で使います)
using ll = long long;
ll connected_componets_size=0;//「グ」連結成分に含まれるマスの数
ll assigned_refernce_number=0;//「グ」現在割り当て中の整理番号
//(DFSをする前に毎度インクリメントするので実際には1からはじまります)
vector<vector<ll>> reference_nums;/*「グ」各連結成分に振られた整理番号をマスごとに保持する
reference_nums[i][j]:マス(i,j)が属する連結成分の整理番号 を表す*/
//"整理番号"を英語でいうと"reference number"らしいです(知らなかった)
map<ll,pair<ll,ll>> color_and_quantity;
//color_and_quantity[整理番号]={色,マスの数};を表す
map<ll,pair<ll,ll>> representatives;
//representatives[整理番号]={上から何番目,左から何番目};を表す
for(ll i=1;i<=H;i++){
for(ll j=1;j<=W;j++){
if(reference_nums[i][j]>0){continue;}//すでに整理番号が振られていたら、DFSを行う意味はないのです
//…ということでスキップします!
else{//さもなくば…
connected_componets_size=0;//連結成分中のマスの数を0にして初期化
assigned_refernce_number++;//割り当て中の整理番号を更新
DFS(i,j,A[i][j]);//DFS、やります
color_and_quantity[assigned_refernce_number]={A[i][j],connected_componets_size};//帰ってきた情報を記録。
representatives[assigned_refernce_number]={i,j};//代表座標も記録しときましょう
}
}
そして、肝心のDFS関数はこちら…!
//4近傍の座標の差分をひとまとめにしました!
vector<ll> di={1,0,-1,0};
vector<ll> dj={0,-1,0,1};
void DFS(ll nowi,ll nowj,ll wanted_color){
//いま、マス(nowi,nowj)を見ているとします。
if(reference_nums[nowi][nowj]>0){return ;}
//すでに整理番号が振られていたらスキップ!これがないと無限ループしてしまいます…。
else{
connected_componets_size++;//同じ連結成分内に新たなマスを発見したので1増やす
reference_nums[nowi][nowj]=assigned_refernce_number;
//マス(nowi,nowj)が属する連結成分に振られた整理番号を記録
for(ll i=0;i<4;i++){//4近傍について調べます
if(1<= nowi+di[i] and nowi+di[i]<=H and 1<=nowj+dj[i] and nowj+dj[i]<=W){
//移動先が範囲内ならば…移動先の色を調べて、
//色が今探してるものと同じなら遷移
if(A[nowi+di[i]][nowj+dj[i]]==wanted_color){
DFS(nowi+di[i],nowj+dj[i],wanted_color);
}
}
}
return ;
}
}
これにてPart1.終了です!つぎいきましょー!!!
Part2.「各連結成分が、他の連結成分とどのようにつながっているかをDFSで記録する!」
連結成分がいくつあるかはassigned_reference_number君が持っています。それぞれ連結成分の代表座標のマスからDFSを進めて、異なる連結成分との隣接がわかったらそれの整理番号をとりあえず全部vectorにぶち込みます!!後で重複を削除します!
vector<vector<bool>> visited;
//「グ」visitedは無限ループに陥るのを防ぐための目印
//visited[i][j]はマス(i,j)にすでに到達したかを表す
vector<vector<ll>> graph;
//「グ」graphでは、各連結成分の隣接関係を管理する
visited.resize(H+1);
for(ll i=1;i<=H;i++){//visitedの初期化
visited.at(i).resize(W+1,false);
}//visitedを適切に初期化
graph.resize(assigned_refernce_number+1);//graphも初期化
//連結成分の数だけ、隣接関係<ドラマ>がある
for(ll i=1;i<=assigned_refernce_number;i++){
pair<ll,ll> coord=representatives[i];
//整理番号i番の連結成分の代表座標を表す
DFS_2(coord.first,coord.second,i);
//DFS,やります!整理番号i番以外と隣り合ってるならvector突っ込むで!
//(詳細は後ほどのDFS_2関数を参照してください)
}
for(ll i=1;i<=assigned_refernce_number;i++){
//隣接関係のリストの要素のうち、重複しているものは削除。これでもなぜか間に合います
sort(ALL(graph[i]));//そーと、結構大事
graph[i].erase(unique(graph[i].begin(), graph[i].end()), graph[i].end());
}
そしてDFS_2関数のご紹介!!先ほどのDFS関数とは異なるものです。
void DFS_2(ll nowi,ll nowj,ll ref_num){
//ref_num:現在注目中の連結成分に割り振られた整理番号
//(reference_numberはながいので)
if(visited[nowi][nowj]==true){return ;}//もう来たところならスキップ
//先ほどと同様、これがないと無限ループに…(>_<)
else{//さもなくば…
visited[nowi][nowj]=true;//来たことを記録
for(ll i=0;i<4;i++){//4近傍を探索
if(1<= nowi+di[i] and nowi+di[i]<=H and 1<=nowj+dj[i] and nowj+dj[i]<=W){
//di,djはさっきのと同じです!
//移動先が範囲内ならば
//移動先の整理番号を調べる
if(reference_nums[nowi+di[i]][nowj+dj[i]]==ref_num){
//移動先のマスの整理番号が注目中のマスのものに等しければ…遷移する!
DFS_2(nowi+di[i],nowj+dj[i],ref_num);
}
else{//さもなくば…!
//整理番号ref_num番の連結成分に隣接する連結成分として登録!
graph.at(ref_num).push_back(reference_nums[nowi+di[i]][nowj+dj[i]]);
}
}
}
return ;
}
Part2.終了!!お次はラストのPart3!
Part3.「各連結成分について、隣接する連結成分の状況をみて、最善の行動をとると何点取れるかを決定する!」
これは正直コードがすべてですね…。説明がなくともみなさんなんとなくわかると思います…!
一応日本語にしてみると、各連結成分について隣接する連結成分に何色が何個あるかを記録して、「その最大値と現在注目している連結成分のマスの数の和」が答えの候補となる、ということです。(伝われ)
ll ans=0;//最終的に出力する答え
ll looking;//現在注目中の連結成分のマスの数
for(ll i=1;i<=assigned_refernce_number;i++){//整理番号を1から順に動かして探索!
looking=color_and_quantity[i].second;//整理番号i番の連結成分のマスの数
map<ll,ll> surrounding_color_and_quantity;//隣接する連結成分に含まれるマスの色と、その合計の数
for(ll a:graph[i]){//隣接しているすべての連結成分についてやります!
surrounding_color_and_quantity[color_and_quantity[a].first]+=color_and_quantity[a].second;
//<補足>
//color_and_quantity[a].first:整理番号a番の連結成分の色
//color_and_quantity[a].second:整理番号a番の連結成分のマスの数
}
ll maxel=0;//max_elementのこと
for(auto b:surrounding_color_and_quantity){
maxel=max(maxel,b.second);
}//全部の色の中で、どれが一番多く存在するかを調べる!
ans=max(ans,maxel+looking);//答えを適切に更新!
}
cout<<ans<<endl;//そして出力!!!
//おつかれさまでした!!
てな感じで解けます!!
4.コード全容
一応全部載せます!
// JOI2022/2023 二次予選 C - 塗りつぶし (Painting)
#include <bits/stdc++.h>
using namespace std;
//それぞれ、こんな感じに短縮しています…!
using ll = long long;
#define ALL(a) (a).begin(),(a).end()
using v_vll = vector<vector<ll>>;
//
//4近傍の座標の差分をひとまとめにしました!
vector<ll> di={1,0,-1,0};
vector<ll> dj={0,-1,0,1};
//
ll H,W;
ll connected_componets_size=0;//連結成分に含まれるマスの数
v_vll reference_nums;//各連結成分に振られた整理番号をマスごとに保持する
v_vll A;//与えられた盤面を保持する
ll assigned_refernce_number=0;//現在割り当て中の整理番号
//(DFSをする前に毎度インクリメントするので実際には1からはじまります)
void DFS(ll nowi,ll nowj,ll wanted_color){
if(reference_nums[nowi][nowj]>0){return ;}
else{
connected_componets_size++;
reference_nums[nowi][nowj]=assigned_refernce_number;
for(ll i=0;i<4;i++){
if(1<= nowi+di[i] and nowi+di[i]<=H and 1<=nowj+dj[i] and nowj+dj[i]<=W){
//移動先が範囲内ならば…移動先の色を調べる
if(A[nowi+di[i]][nowj+dj[i]]==wanted_color){
DFS(nowi+di[i],nowj+dj[i],wanted_color);
}
}
}
return ;
}
}
vector<vector<bool>> visited;
v_vll graph;
//visitedは無限ループに陥るのを防ぐための目印
//graphでは、各連結成分の隣接関係を管理する
void DFS_2(ll nowi,ll nowj,ll ref_num){
//ref_num:現在注目中の連結成分に割り振られた整理番号
//(reference_numberはながいので)
if(visited[nowi][nowj]==true){return ;}
else{
visited[nowi][nowj]=true;
for(ll i=0;i<4;i++){
if(1<= nowi+di[i] and nowi+di[i]<=H and 1<=nowj+dj[i] and nowj+dj[i]<=W){
//移動先が範囲内ならば
//移動先の整理番号を調べる
if(reference_nums[nowi+di[i]][nowj+dj[i]]==ref_num){
//移動先のマスの整理番号が注目中のマスのものに等しければ
DFS_2(nowi+di[i],nowj+dj[i],ref_num);
}
else{
//隣接する連結成分として登録!
graph.at(ref_num).push_back(reference_nums[nowi+di[i]][nowj+dj[i]]);
}
}
}
return ;
}
}
int main(){
cin>>H>>W;
reference_nums.resize(H+1);
for(ll i=1;i<=H;i++){
reference_nums.at(i).resize(W+1,-1);
}
A.resize(H+1);
for(ll i=1;i<=H;i++){
A.at(i).resize(W+1);
}
for(ll i=1;i<=H;i++){
for(ll j=1;j<=W;j++){
cin>>A[i][j];
}
}
//Part.1 START>>
map<ll,pair<ll,ll>> color_and_quantity;
map<ll,pair<ll,ll>> representatives;
for(ll i=1;i<=H;i++){
for(ll j=1;j<=W;j++){
if(reference_nums[i][j]>0){continue;}
else{
connected_componets_size=0;
assigned_refernce_number++;
DFS(i,j,A[i][j]);
color_and_quantity[assigned_refernce_number]={A[i][j],connected_componets_size};
representatives[assigned_refernce_number]={i,j};
}
}
}
//<<Part1.END
//Part2.START>>
visited.resize(H+1);
graph.resize(assigned_refernce_number+1);//連結成分の数だけ、ドラマがある
for(ll i=1;i<=H;i++){//visitedの初期化
visited.at(i).resize(W+1,0);
}
for(ll i=1;i<=assigned_refernce_number;i++){
pair<ll,ll> coord=representatives[i];
DFS_2(coord.first,coord.second,i);
}
for(ll i=1;i<=assigned_refernce_number;i++){
//隣接リストのうち、重複しているものは削除。これでもなぜか間に合います
sort(ALL(graph[i]));
graph[i].erase(unique(graph[i].begin(), graph[i].end()), graph[i].end());
}
//<<Part2.END
//Part3.START>>
ll ans=0;
ll looking;//現在注目中の連結成分のマスの数
for(ll i=1;i<=assigned_refernce_number;i++){
looking=color_and_quantity[i].second;
map<ll,ll> surrounding_color_and_quantity;//隣接する連結成分に含まれるマスの色と、その合計の数
for(ll a:graph[i]){
surrounding_color_and_quantity[color_and_quantity[a].first]+=color_and_quantity[a].second;
//<補足>
//color_and_quantity[a].first:整理番号aの連結成分の色
//color_and_quantity[a].second:整理番号aの連結成分のマスの数
}
ll maxel=0;//max_element
for(auto b:surrounding_color_and_quantity){
maxel=max(maxel,b.second);//めっちゃ遅そうだけど、間に合うんですね~~
}
ans=max(ans,maxel+looking);
}
cout<<ans<<endl;
//おつかれさまでした!!
}
結構長くなりましたね笑笑
ところどころ遅そうなところはありますけど、これをそのまま貼り付けるとACが得られます!!
5.おわりに
私が本番中にこの問題に取り組んでいるときは取り組み始めてからかなり時間がたっていたこともあり「もう無理かな…」という気持ちが一瞬よぎったのですがあきらめずに自分が今持っている知識と技術で何とかACをもぎ取ることができました!!まさに、解けたが届いた瞬間でしたね…!(AtCoder社の問題ではないですけどね笑)同時に、自分の知識不足も感じたので今後精進します…。!!
未来のJOIerや、その他競プロerの役に立てたらと思い筆を執りました。何か疑問があればせるたわーしーぷ(Twitter:@LaserTHETA)にリプなりDMなりメンションなり飛ばしていただけるとお答えします!そして、何か間違いがあったらできる限り速やかに直しますのでこちらも何らかの方法でわたくしまで連絡を頂けたらと思います。
JOIの作問担当の方、そしてここまで読んでくださった方、本当にありがとうございました!!
2022/12/19 せるたわーしーぷ!