はじめに
- 自らの学習のため、Pythonでゼロから生成モデル(VAE, GAN, Diffusion Model)を作成した備忘録です。
- 下図のような、大きさの異なる星型の図形(座標)を生成することが生成モデルの目標です。
- 間違いがあれば、ご指摘頂けますと幸いです。
学習データ (対象とする生成物)
- 星型の図形は頂点座標 (x, y) * 5点 = 10個のパラメータで定義されます。
- 画像データではありません。
| Node | x座標 | y座標 |
|---|---|---|
| N1 | x1 | y1 |
| N2 | x2 | y2 |
| N3 | x3 | y3 |
| N4 | x4 | y4 |
| N5 | x5 | y5 |
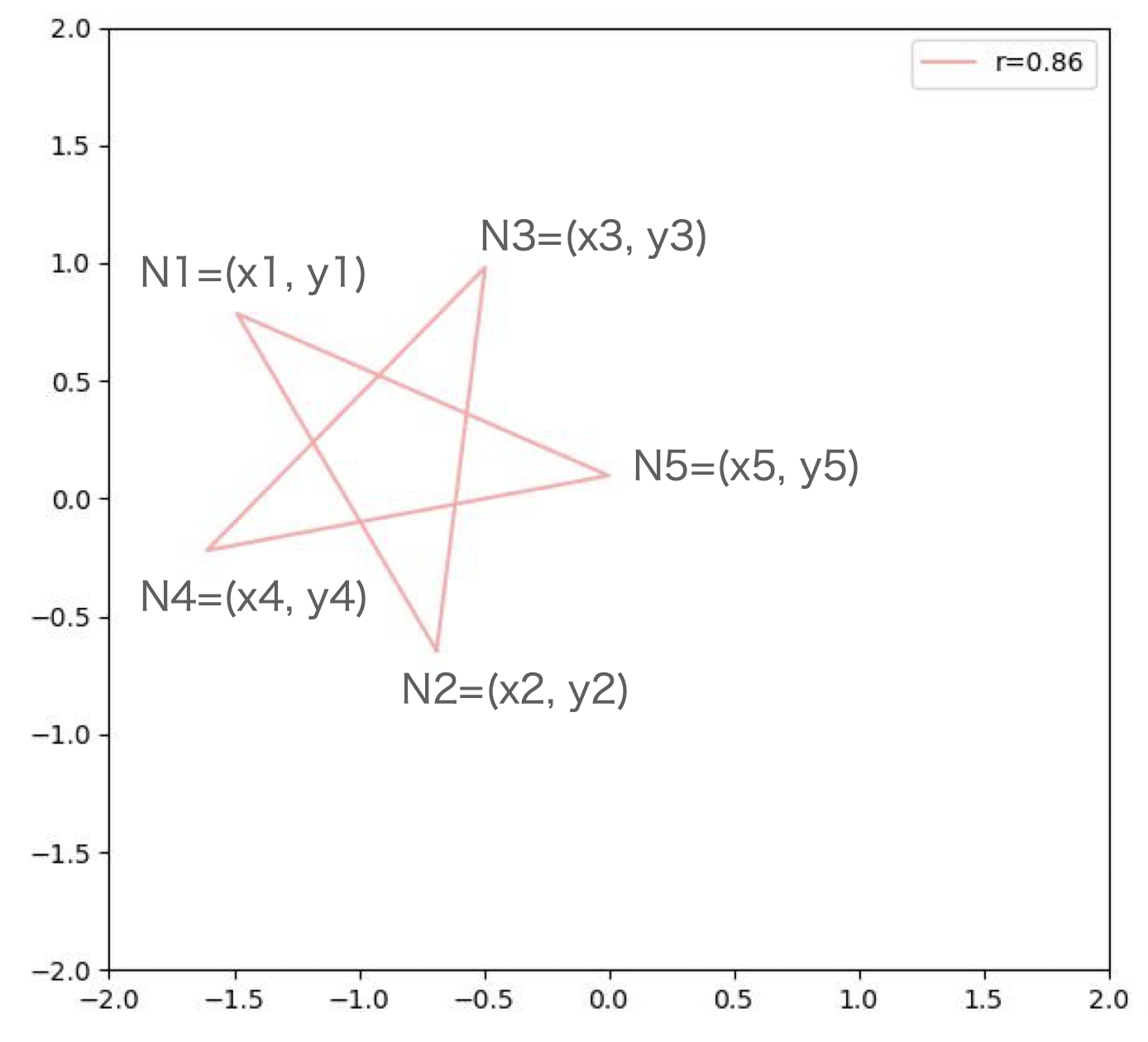
このような図形をランダムに約1000件作成して、学習データとします。
学習データに使う星型の座標データはこちらのコードを利用して、作成しています。
星型形状の中心座標(①x, ②y)、外接円の③半径、④傾きをランダムに決めて、座標値を計算して求めています。
ですので、学習データとして使う星型座標は全部で10個のパラメータになりますが、実際には4つのパラメータで説明できることになります。
# %%==========================================================================
# libraries
# ============================================================================
# default
import os
import random
import math
# additional
import numpy as np
import torch
import matplotlib.pyplot as plt
# %%==========================================================================
# 星型の座標をランダムに生成する関数
# ============================================================================
def generate_star_shape_coord_data(num_data, seed):
"""num_data数だけランダムに中心座標と半径を決めて、星型の頂点座標5点と半径情報を返す
Args:
num_data (int): 生成するデータ数
seed (int): ランダムシード
Returns:
(torch.tensor, torch.tensor): 座標、外接円の半径
"""
# ランダムシードの固定
random.seed(seed)
torch.manual_seed(seed)
# 半径、中心xy座標、最初の点の開始角度をランダムに決めて、torch tensorにする
radiuses = [random.uniform(0.1, 1) for _ in range(num_data)]
coord_xs = [random.uniform(-1, 1) for _ in range(num_data)]
coord_ys = [random.uniform(-1, 1) for _ in range(num_data)]
begin_angles = [random.uniform(0, 2*math.pi) for _ in range(num_data)]
radiuses = torch.tensor(radiuses)
coord_xs = torch.tensor(coord_xs)
coord_ys = torch.tensor(coord_ys)
begin_angles = torch.tensor(begin_angles)
# 中心座標と半径から星型の点列データを作る -> 学習データのX
coord_data = torch.zeros([num_data, 2, 5])
for i in range(5):
coord_data[:, 0, i] = radiuses * torch.cos(begin_angles + 4*math.pi/5*i) + coord_xs
coord_data[:, 1, i] = radiuses * torch.sin(begin_angles + 4*math.pi/5*i) + coord_ys
return coord_data, radiuses
自動で生成する関数を呼び出して、Dataset、Dataloaderを作成する関数も作っておきます。
この関数は、VAE, GAN, Diffusionの学習で同じものを使います。
なお、関数create_dataloaderはtrain用のdataloaderとvalidation用のdataloaderが入った辞書を返すように作っているのでご注意ください。
# %%==========================================================================
# Dataset
# ============================================================================
class DataSet(torch.utils.data.Dataset):
def __init__(self, num_data, seed):
self.num_data = num_data
self.X, self.y = generate_star_shape_coord_data(num_data, seed)
self.X = self.X.unsqueeze(1)
self.y = self.y.unsqueeze(1)
def __getitem__(self, idx):
return self.X[idx,...], self.y[idx,...]
def __len__(self):
return self.X.shape[0]
def create_dataloader(train_num, valid_num, batch_size):
datasets = {"train": DataSet(train_num, seed=2023), "valid": DataSet(valid_num, seed=1)}
dataloader_train = torch.utils.data.DataLoader(datasets["train"],
batch_size=batch_size,
shuffle=True,
drop_last=True)
dataloader_valid = torch.utils.data.DataLoader(datasets["valid"],
batch_size=batch_size,
shuffle=False,
drop_last=True)
return {"train": dataloader_train, "valid": dataloader_valid}
また、ここで生成した星型データをグラフ化して、図として保存する関数も作っておきます。
各トレーニングにおいて、数epoch毎にこの関数を呼び出して、途中経過を確認するのに使っています。
# %%==========================================================================
# 星型のデータを描画して保存する関数
# 生成モデルの学習中に利用できるように、epoch数
# ============================================================================
def save_star_coord_graphs(log_dir, epoch, r, data1, data2=None, s=4):
"""星型の座標値をグラフ化して、保存する関数
Args:
log_dir (str): 保存ディレクトリ
epoch (int): ファイル名に追加する番号
r (tensor): 外接円の半径
data1 (tensor): 座標情報、2つ以上入力する
data2 (tensor, optional): 座標情報. 重ねて2つ表示する場合は指定する. Defaults to None.
VAEの学習データと再構成データを重ねて表示するときに利用
s (int, optional): 1データのグラフサイズ. Defaults to 4.
"""
num_graphs = data1.shape[0]
warning_num = 64
if num_graphs > warning_num:
# 間違って大量に渡すと時間が非常にかかるので、保険で確認メッセージを出す
if input(f"グラフ表示する数が{warning_num}以上ありますが続けますか? [y/n]") != "y":
print("グラフ表示をキャンセルしました")
return
num_row = int(num_graphs ** 0.5)
num_col = (num_graphs - 1) // num_row + 1
data1 = torch.concat([data1, data1[:,:,:,:1]], dim=3)
data1 = data1.detach().numpy()
if data2 is not None:
data2 = torch.concat([data2, data2[:,:,:,:1]], dim=3)
data2 = data2.detach().numpy()
fig, axs = plt.subplots(num_row, num_col, figsize=(num_col*s, num_row*s),
tight_layout=True, sharex=True, sharey=True)
ax = axs.ravel()
for i in range(num_graphs):
ax[i].plot(data1[i, 0, 0, :], data1[i, 0, 1, :], c="#ffaaaa", label=f"r={r[i].item():.2f}")
ax[i].set_xlim(-2, 2)
ax[i].set_ylim(-2, 2)
if data2 is not None:
ax[i].plot(data2[i, 0, 0, :], data2[i, 0, 1, :], c="#aaaaff")
ax[i].set_xlim(-2, 2)
ax[i].set_ylim(-2, 2)
ax[i].legend()
fig.suptitle(f"epoch={epoch:06d}", size=15)
fig.savefig(os.path.join(log_dir, "hist", f"star_graphs_epoch_{epoch:06d}.jpg"))
fig.savefig(os.path.join(log_dir, f"star_graphs_epoch_latest.jpg"))
plt.clf()
plt.close()
if __name__ == "__main__":
save_dir = r"star_imgs"
os.makedirs(save_dir, exist_ok=True)
os.makedirs(os.path.join(save_dir, "hist"), exist_ok=True)
dataloaders = create_dataloader(100, 10, 2)
for x, y in dataloaders["train"]:
save_star_coord_graphs(save_dir, 0, y, x, s=6)
break
ここまでの関数を使って生成した学習データの一部を次に示します。
- 星型の外接円の半径をrとして、グラフの凡例としています。
- 作成する生成モデルはrを条件として与えて、中心位置や角度が異なる星型を生成することを目標とします。
VAE
VAEの詳細は、他に色々と分かりやすいwebページがあるので省略しますが、
教師データ情報を、Encoderで情報圧縮し、Decoderで復元する機構です。
今回は、条件付きで生成して欲しいので、潜在変数変数の他に(潜在変数の一部として)、条件を示すパラメータを追加します。下図の条件(c)です。
- 条件(c)が大きさ情報になるように
- 成した座標情報が星型形状を示すように
- 潜在変数が正規分布に従うように
Lossを設定して、学習していきます。
ここから、VAEの学習コードを説明していきます。
コードは次のように小分けにしてそれぞれを簡単に説明します。
- ネットワークモデル
- Encoder
- Decoder
- VAE(EncoderとDecoderの合体)
- ハイパーパラメータの設定
- パラメータと結果の出力
- 学習を実施する関数
- 結果
ネットワークモデル
エンコーダー
入力データサイズ : (batch_size, 1, 2, 5)
これをエンコーダーを通すことで、次の3つのデータに変換します。
| パラメータ | 説明 | 出力サイズ |
|---|---|---|
| c | 条件(今回は半径) | (batch_size, 1) |
| mean | 潜在変数の平均 | (batch_size, z_dim) |
| log_var | 潜在変数の分散(log) | (batch_size, z_dim) |
cは潜在変数の一つであるイメージでこのように組んだのですが、
エンコーダーで学習することなく、教師データの値をそのままデーコーダーに渡してもいいのかもしれません。
今回は、VAE, GAN, Diffusion いずれも、最初にreshapeして1次元に変換して、MLPを使います。
2次元配列とみなせるのでConv2dを使ってもいいと思いますが、今回は簡単であることを優先しました。
Encoderでは、最後にmean, log_var, condition を予測する線形変換をそれぞれ作っている点が特徴的です。
# %%==========================================================================
# VAE Network
# ============================================================================
class Encoder(nn.Module):
def __init__(self, chs, z_dim, c_dim):
"""星型座標情報を潜在変数に変換する。
潜在変数は平均値と分散の2つを返す
Args:
chs (list): チャンネル数をリストで設定する
z_dim (int): 潜在変数の次元数
c_dim (int): 生成条件の次元。今回は半径だけなので1次元
"""
super().__init__()
self.enc = nn.Sequential()
chs = [10] + chs
for idx, (in_ch, out_ch) in enumerate(zip(chs[:-1], chs[1:])):
# 線形変換と活性化関数を繰り返す
self.enc.add_module(f"enc_linear_{idx:02d}", nn.Linear(in_ch, out_ch))
self.enc.add_module(f"enc_relu_{idx:02d}", nn.LeakyReLU(0.1, inplace=True))
# 半径、潜在変数の平均、分散を求める線形変換をそれぞれ定義する
self.enc_out_condition = nn.Linear(chs[-1], c_dim)
self.enc_out_mean = nn.Linear(chs[-1], z_dim)
self.enc_out_log_var = nn.Linear(chs[-1], z_dim)
def forward(self, x):
x = x.reshape(-1, 10)
x = self.enc(x)
c = self.enc_out_condition(x)
m = self.enc_out_mean(x)
v = self.enc_out_log_var(x)
return c, m, v
デコーダー
潜在変数zと条件cから星型座標データを生成します。
Reparameterization Trickでの潜在変数z作成は後述します。
最初にzとcをつなげています。
条件cは最後の出力前にも情報として渡しています(色々試行錯誤してこうなりました)。
class Decoder(nn.Module):
def __init__(self, chs, z_dim, c_dim):
"""デコーダー
潜在変数と条件値から星型座標を生成する
Args:
chs (list): チャンネル数をリストで設定する
z_dim (int): 潜在変数の次元数
c_dim (int): 生成条件の次元。今回は半径だけなので1次元
"""
super().__init__()
self.dec = nn.Sequential()
chs = [z_dim + c_dim] + chs # 最初の入力は潜在変数と条件をつなげたデータにする
for idx, (in_ch, out_ch) in enumerate(zip(chs[:-1], chs[1:])): # chsを一つずつずらしてin out のチャンネル数としてループ
self.dec.add_module(f"dec_linear_{idx:02d}", nn.Linear(in_ch, out_ch, bias=False))
self.dec.add_module(f"dec_bn_{idx:02d}", nn.BatchNorm1d(out_ch))
self.dec.add_module(f"dec_relu_{idx:02d}", nn.LeakyReLU(0.1, inplace=True))
self.dec_out = nn.Linear(chs[-1]+1, 10)
def forward(self, z, c):
x = torch.cat([z, c], dim=1)
x = self.dec(x)
x = torch.cat([x, c], dim=1)
x = self.dec_out(x)
x = x.reshape(-1, 1, 2, 5)
return x
VAE
エンコーダー、デコーダを繋げてVAEのネットワークを作成します。
分散と平均からzを抽出するReparameterization Trickは、sampling_z()メソッドで定義しています。
loss値の計算には最終的な再構築データ以外の情報も必要なので、returnで全部返しています。
class VAE(nn.Module):
def __init__(self, chs_e, chs_d, z_dim, c_dim):
super().__init__()
self.encoder = Encoder(chs_e, z_dim, c_dim)
self.decoder = Decoder(chs_d, z_dim, c_dim)
def forward(self, x):
# 星型座標値 -> 半径、潜在変数の平均と分散
c, mean, log_var = self.encoder(x)
# 平均と分散 -> 潜在変数
z = self.sampling_z(mean, log_var)
# 潜在変数と半径 -> 再構築 星型座標値
y = self.decoder(z, c)
return c, mean, log_var, y
def sampling_z(self, mean, log_var):
epsilon = torch.randn(log_var.shape, device=log_var.device)
z = mean + epsilon * torch.exp(0.5*log_var)
return z
# 動作確認
if __name__ == "__main__":
z_dim, c_dim = 2, 1
batch_s = 3
chs = [8, 4, 2]
vae = VAE(chs, chs, z_dim, c_dim)
x = torch.randn([batch_s, 1, 2, 5])
c, mean, log_var, y = vae(x)
print(f"{c.shape=}")
print(f"{mean.shape=}")
print(f"{log_var.shape=}")
print(f"{y.shape=}")
z = torch.randn([batch_s, z_dim])
c = torch.ones([batch_s, c_dim]) * 0.5
y2 = vae.decoder(z, c)
print(f"{y2.shape=}")
ハイパーパラメータの設定
ハイパーパラメータは、dataclassで管理することにします。
ハイパーパラメータの管理方法はいつも悩みます・・・。
@dataclass
class HyperParameters:
task_name: str = "vae_01" # 結果を保存するフォルダ名
epochs: int = 500 # epoch数
img_save_steps: int = 20 # 途中結果画像を保存する回数
batch_size: int = 128 # バッチサイズ
lr: float = 5e-3 # 学習率
z_dim: int = 4 # 潜在変数の次元
c_dim: int = 1 # 条件の次元
num_train_data: int = 800 # trainingデータの数
num_valid_data: int = 200 # validationデータの数
# エンコーダーのlayerのチャンネル数
enc_chs: list = field(default_factory=lambda: [16, 32, 64, 32, 16])
# デコーダーのlayerのチャンネル数
dec_chs: list = field(default_factory=lambda: [16, 32, 64, 32, 16])
alpha: float = 2e-4 # KLダイバージェンスにかける係数
beta: float = 1.0 # コンディションにLossにかける係数
patience: int = 0 # この回数以上validation lossが改善しない場合学習を終了する
comment: str = "" # 任意コメント(いつも修正し忘れて混乱するからない方がいいのに、ついつい欄を作ってしまう)
パラメータと結果の出力
このあとで説明する学習関数を呼び出す前に実行します。
ハイパーパラメータのインスタンスを渡すことで、Task名のフォルダを作り、
パラメータをjson形式で保存します。
def training_log_settings(params):
# タスクの保存フォルダ
log_dir = os.path.join(r"./", "log", params.task_name)
os.makedirs(log_dir, exist_ok=True)
# epoch, iter毎のデータは多くなるので別フォルダを作る (途中の生成画像を保存する)
log_dir_hist = os.path.join(log_dir, "hist", params.task_name)
os.makedirs(log_dir_hist, exist_ok=True)
# 設定ファイルの保存
with open(os.path.join(log_dir, "parameters.json"), 'w') as f:
json.dump(vars(params), f, indent=4)
params = HyperParameters()
training_log_settings(params)
学習関数
学習は、基本的には分類や回帰のAIと同様です。
各epochでtrain, validを順番に回し、予測、lossの算出、誤差逆伝播という流れです。
VAEではlossの算出が特殊になります。
実は再構築誤差の計算がよくわかっていません。
今回はMSEを使いました。VAEとしては間違っているかもしれませんが、うまく生成できたからOKとしています。
すみません。
def vae_training(params):
# 先に定義した関数でx:星型座標とy:外接円半径を返すデータローダーを作成する
dataloaders = create_dataloader(params.num_train_data, params.num_valid_data, params.batch_size)
# 通常の分類予測と同様に、モデル、optimizer、loss関数を定義
vae = VAE(params.enc_chs, params.dec_chs, params.z_dim, params.c_dim)
optimizer = torch.optim.Adam(vae.parameters(), lr=params.lr)
optimizer.zero_grad()
loss_fn = torch.nn.MSELoss()
# 色々データ保存用の準備
loss_logger = {"train": {"loss": [], "kl":[], "recons": [], "radius": []},
"valid": {"loss": [], "kl":[], "recons": [], "radius": []}}
log_dir = os.path.join("./", "log", params.task_name)
model_path = os.path.join(log_dir, f"model_weight_on.pt")
# 途中での確認用使う潜在変数と半径
sampling_z = torch.randn([9, params.z_dim])
sampling_r = torch.linspace(0.2, 1.0, 9).unsqueeze(1)
# VAEに通して、ロスを求めるところまでを関数化 train, validationで2回呼び出す
def forward_process(x, r):
r_out, mean, log_var, y_out = vae(x)
kl = 0.5 * torch.sum(1 + log_var - mean**2 - torch.exp(log_var))
# 学習がうまく進まないので、MSE Lossを採用した
# reconstruction = torch.sum(x * torch.log(y_out + eps) + (1 - x) * torch.log(1 - y_out + eps))
reconstruction = loss_fn(y_out, x)
loss_r = loss_fn(r, r_out)
loss = -kl * params.alpha + reconstruction + loss_r * params.beta
return loss, (-kl.item(), reconstruction.item(), loss_r.item())
# lossはKL, 再構築誤差、半径、合計、それぞれをモニタリングできるように保存するための関数(iter毎)
def store_temporary_losses(loss_logs, loss_log):
loss_logs[0] += loss_log[0]
loss_logs[1] += loss_log[1]
loss_logs[2] += loss_log[2]
return loss_logs
# lossはKL, 再構築誤差、半径、合計、それぞれをモニタリングできるように保存するための関数(epoch毎)
def store_loss(loss_logs, loss_logger, turn):
loss_logger[turn]["kl"].append(loss_logs[0] / (iter + 1))
loss_logger[turn]["recons"].append(loss_logs[1] / (iter + 1))
loss_logger[turn]["radius"].append(loss_logs[2] / (iter + 1))
loss_logger[turn]["loss"].append(loss_logger[turn]["kl"][-1]
+ loss_logger[turn]["recons"][-1]
+ loss_logger[turn]["radius"][-1])
return loss_logger
# 学習
loss_min = 9e+9
loss_stagnation = 0
epoch_bar = tqdm(range(1, params.epochs+1))
for epoch in epoch_bar:
epoch_bar.set_description(f"Epoch:{epoch}")
loss_logs = [0, 0, 0]
iter_bar = tqdm(dataloaders["train"], leave=False)
for iter, (x, r) in enumerate(iter_bar):
vae.train()
loss, loss_log = forward_process(x, r)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_logs = store_temporary_losses(loss_logs, loss_log)
loss_logger = store_loss(loss_logs, loss_logger, "train")
loss_logs = [0, 0, 0]
iter_bar = tqdm(dataloaders["valid"], leave=False)
for iter, (x, r) in enumerate(iter_bar):
vae.eval()
with torch.no_grad():
loss, loss_log = forward_process(x, r)
loss_logs = store_temporary_losses(loss_logs, loss_log)
loss_logger = store_loss(loss_logs, loss_logger, "valid")
save_loss_list_graph(log_dir, loss_logger)
if epoch % max(1, (int(params.epochs / params.img_save_steps))) == 0:
_, _, _, y_out = vae(x[:9])
save_star_coord_graphs(log_dir, epoch, r=r[:9], data1=x[:9], data2=y_out, s=2)
if loss_min > loss_logger["valid"]["loss"][-1]:
loss_min = loss_logger["valid"]["loss"][-1]
torch.save(vae.state_dict(), model_path)
loss_stagnation = 0
else:
loss_stagnation += 1
epoch_bar.set_postfix({"loss": f"{loss.item():.2e}",
"loss_kl": f"{loss_log[0]:.2e}",
"loss_recons": f"{loss_log[1]:.2e}",
"loss_r": f"{loss_log[2]:.2e}",
})
if params.patience and loss_stagnation > params.patience:
break
# 再構築ではなく、ランダムに決めた潜在変数と0.1毎の半径を与えて生成してみる
out = vae.decoder(sampling_z, sampling_r)
save_star_coord_graphs(log_dir, 99999, r=sampling_r, data1=out, s=2)
# epoch毎のlossデータを書き出す関数。epoch毎に呼び出す
# 学習実施中に書き込みできなくなるツールで開くと書き込みエラーになるので注意。
# VSCodeで表示しておけば、逐次更新して最新状態が表示される
def save_loss_list_graph(log_dir, loss_logger):
fig, ax = plt.subplots(1,1)
epoch = range(len(loss_logger["train"]["loss"]))
ax.plot(epoch, loss_logger["train"]["loss"], label="train_loss")
ax.plot(epoch, loss_logger["train"]["kl"], label="train_kl")
ax.plot(epoch, loss_logger["train"]["recons"], label="train_recons")
ax.plot(epoch, loss_logger["train"]["radius"], label="train_radius")
ax.plot(epoch, loss_logger["valid"]["loss"], label="valid_loss")
ax.plot(epoch, loss_logger["valid"]["kl"], label="valid_kl")
ax.plot(epoch, loss_logger["valid"]["recons"], label="valid_recons")
ax.plot(epoch, loss_logger["valid"]["radius"], label="valid_radius")
ax.legend()
fig.savefig(os.path.join(log_dir, "loss_history.jpg"))
plt.clf()
plt.close()
結果
必要な関数を呼び出して、学習を実行します
params = HyperParameters()
training_log_settings(params)
vae_training(params)
loss推移
重なっていて分かりにくいですが、一番上の紫色の線がvalidationのlossです。
おおよそ100epochあたりから変化が緩やかになり、300epoch頃に最小値を記録しています。
VAEの再構築ができるように色々パラメータを変更しました。
lrが適切でないと、全く再構築できる兆候がみられませんでしたが、lr=5e-3程度に設定すると再構築できるようになりました。
再構築データ
オレンジが学習データ、紫がVAEによる再構築データです。
多少のずれはありますが、大きさ、位置はよく再現できていますし、ちゃんと星型になっています。
このグラフは、生成した座標をn1から順番に一筆書きで描画していますので、順番が異なると綺麗な星型になりません。
生成データ
ランダムな潜在変数を与えて星型を生成した結果です。
大きさは0.2〜1.0まで0.1刻みで設定しています。
きっちりと指定した通りの大きさにはなっていませんが、rに大きな値を設定するほど(グラフの下側が大きい)、
大きな星型になる傾向が見られますし、どれも綺麗な星型が生成できました。キラッ⭐️
- 注意 簡単な条件の割に、学習データ数が多いので、もしかしたら学習データにあるデータを再構築している可能性がありません。時間が取れたら確認してみます。
sampling_z = torch.randn([9, params.z_dim])
sampling_r = torch.linspace(0.2, 1.0, 9).unsqueeze(1)
vae.decoder(sampling_z, sampling_r)
GAN
GANはGenerator(生成器)とDiscriminator(判定器)を競わせて、欲しいデータを生成できるようにGeneratorを成長させる手法です。
### ネットワーク
ジェネレーター
基本的にはVAEのデコーダーと同じです
ハイパーパラメータをいくら変えても即モード崩壊していましたが、BatchNorm1dを加えることで、多様なデータを生成できるようになりました。
class Generator(nn.Module):
def __init__(self, chs, z_dim, c_dim):
super().__init__()
self.gen = nn.Sequential()
chs = [z_dim + c_dim] + chs
for idx, (in_ch, out_ch) in enumerate(zip(chs[:-1], chs[1:])):
self.gen.add_module(f"gen_linear_{idx:02d}", nn.Linear(in_ch, out_ch, bias=False))
self.gen.add_module(f"gen_bn_{idx:02d}", nn.BatchNorm1d(out_ch))
self.gen.add_module(f"gen_relu_{idx:02d}", nn.LeakyReLU(0.1, inplace=True))
self.gen_out = nn.Linear(chs[-1]+1, 10)
def forward(self, z, c):
x = torch.cat([z, c], dim=1)
x = self.gen(x)
x = torch.cat([x, c], dim=1)
x = self.gen_out(x)
x = x.reshape(-1, 1, 2, 5)
return x
ディスクリミネーター
こちらも基本はVAEのEncoderと同じですが、最後の出力はデータがrealかどうかを示す1chの値です
class Discriminator(nn.Module):
def __init__(self, chs, c_dim):
super().__init__()
self.dis = nn.Sequential()
chs = [11] + chs
for idx, (in_ch, out_ch) in enumerate(zip(chs[:-1], chs[1:])):
# self.dis.add_module(f"dis_linear_{idx:02d}", nn.utils.spectral_norm(nn.Linear(in_ch, out_ch)))
self.dis.add_module(f"dis_linear_{idx:02d}", nn.Linear(in_ch, out_ch))
# self.dis.add_module(f"dis_bn_{idx:02d}", nn.BatchNorm1d(out_ch))
self.dis.add_module(f"dis_relu_{idx:02d}", nn.LeakyReLU(0.1, inplace=True))
self.dis_out = nn.Linear(chs[-1] + c_dim, 1)
def forward(self, x, c):
x = x.reshape(-1, 10)
x = torch.cat([x, c], dim=1)
x = self.dis(x)
x = torch.cat([x, c], dim=1)
x = self.dis_out(x)
return x
# test
z_dim, c_dim = 2, 1
chs = [8, 4, 2]
generator = Generator(chs, z_dim, c_dim)
discriminator = Discriminator(chs[::-1], c_dim)
# generate
z = torch.randn(4, 2)
r = torch.ones([4, 1]) * 0.5
fake = generator(z, r)
print(f"{fake.shape=}")
# discriminate
out = discriminator(fake, r)
print(f"{out.shape=}")
学習関数
GANの学習は、Generator, Discriminatorそれぞれについて順番に実施します。
どちらの場合も、
- Generatorがfake画像を生成する
- Discriminatorが画像をfakeかrealか判定する
という手順は一緒です。
- Generatorは、Discriminatorにfakeと見抜かれたことがペナルティになります。
Generatorの生成した偽物の情報をDiscriminatorが読み込んでいるので、偽物であることが正しいですが、
Discriminatorを騙したいGeneratorにとっては、realと判定して欲しいので、"本物"という判定基準との差がlossになります。
- Discriminatorはfake, real画像をそれぞれ判定して、間違いがペナルティです。
こちらは素直にDiscriminatorの判断が正しいかどうかを判定します。
- loss関数には、さまざまな手法が提案されていますが、今回は実装が簡単なHinge Lossを採用しました。
- Generator, Discriminatorそれぞれの学習率lrを調整するのが大変なので、Discriminatorのlrを自動で調整することにしました。先駆者らの知見をインターネットで調べた限り、Generatorの学習具合に合わせてDiscriminatorの学習を調整することは、効果がないと言われている方が多いです。試しに導入してみましたが、あまりいい手法ではないのかも知れません。
def gan_training(params):
dataloaders = create_dataloader(params.num_train_data, params.num_valid_data, params.batch_size)
# generator, discriminatorはそれぞれでモデル、optimizerを準備する
generator = Generator(params.gen_chs, params.z_dim, params.c_dim)
discriminator = Discriminator(params.dis_chs, params.c_dim)
optimizer_g = torch.optim.SGD(generator.parameters(), lr=params.lr_g, weight_decay=1e-6)
optimizer_d = torch.optim.SGD(discriminator.parameters(), lr=params.lr_d, weight_decay=1e-6)
optimizer_g.zero_grad()
optimizer_d.zero_grad()
# loss値に応じてdiscriminatorのlrを調整する関数(あまり良くない?)
lr = params.lr_d
def lr_adjuster(loss_g, loss_d, lr):
ratio = 1.05
if loss_g > 0.4 and loss_d < 1.0:
lr = max(params.lr_d/1000, lr/ratio)
else:
lr = min(params.lr_d*1000, lr*ratio)
for g in optimizer_d.param_groups:
g['lr'] = lr
return lr
loss_logger = {"dis": [], "gen": []}
log_dir = os.path.join(r"./", "log", params.task_name)
# 途中での確認用使う潜在変数と半径
sampling_z = torch.randn([9, params.z_dim])
sampling_r = torch.linspace(0.2, 1.0, 9).unsqueeze(1)
# 学習
epoch_bar = tqdm(range(1, params.epochs+1))
for epoch in epoch_bar:
epoch_bar.set_description(f"Epoch:{epoch}")
loss_log_gen, loss_log_dis = 0, 0
iter_bar = tqdm(dataloaders["train"], leave=False)
for iter, (real, r) in enumerate(iter_bar):
batch_size = real.shape[0]
# generator
z = torch.rand(batch_size, params.z_dim)
fake = generator(z, r)
y_fake = discriminator(fake, r)
# ヒンジロス
loss_g = -torch.mean(y_fake)
optimizer_g.zero_grad()
optimizer_d.zero_grad()
loss_g.backward()
optimizer_g.step()
# discriminator
fake = generator(z, r)
y_fake = discriminator(fake, r)
y_real = discriminator(real, r)
# ヒンジロス
loss_d = F.relu(1.0 - y_real).mean() + F.relu(1.0 + y_fake).mean()
optimizer_d.zero_grad()
loss_d.backward()
lr = lr_adjuster(loss_g.item(), loss_d.item(), lr)
optimizer_d.step()
iter_bar.set_postfix({"loss_gen": f"{loss_g:.2e}", "loss_dis": f"{loss_d:.2e}"})
# log
loss_log_gen += loss_g.item()
loss_log_dis += loss_d.item()
loss_logger["gen"].append(loss_log_gen / (iter + 1))
loss_logger["dis"].append(loss_log_dis / (iter + 1))
epoch_bar.set_postfix({"loss_gen": f"{loss_logger['gen'][-1]:.2e}", "loss_dis": f"{loss_logger['dis'][-1]:.2e}", "lr":f"{lr:.1e}"})
save_loss_list_graph(log_dir, loss_logger)
if epoch % max(1, (int(params.epochs / params.img_save_steps))) == 0:
out = generator(sampling_z, sampling_r)
save_star_coord_graphs(log_dir, epoch, r=sampling_r, data1=out, s=2)
def save_loss_list_graph(log_dir, loss_logger):
fig, ax = plt.subplots(1,1)
epoch = range(len(loss_logger["gen"]))
ax.plot(epoch, loss_logger["gen"], label="generator")
ax.plot(epoch, loss_logger["dis"], label="discriminator")
ax.set_ylim(-1, 2)
ax.legend()
fig.savefig(os.path.join(log_dir, "loss_history.jpg"))
plt.clf()
plt.close()
ハイパーパラメータ
基本はVAEと一緒です。一般的にはgeneratorとdiscriminatorでlrをそれぞれ設定します。
@dataclass
class HyperParameters:
task_name: str = "gan_01"
epochs: int = 2000
img_save_steps: int = 20
batch_size: int = 128
lr_g: float = 5e-4
lr_d: float = 5e-4
z_dim: int = 2
c_dim: int = 1
num_train_data: int = 1000
num_valid_data: int = 0
gen_chs: list = field(default_factory=lambda: [16, 64, 128, 64, 16])
dis_chs: list = field(default_factory=lambda: [16, 64, 64, 32])
comment: str = ""
結果
loss推移
generatorのlossが0.5程度 (Discriminatorの正答率が50%程度)で学習が進んでいます。
lrが小さいと、generatorのlossが0である状態が長く続いて学習が進まず、
反対にlrが大きすぎると、generatorのlossが過ぐに1になり(Discriminatorが勝ちすぎて)学習が進みません。
VAE, GAN, Diffusionの中でGANが一番苦労しました。
生成データ
綺麗な星型が生成できました。
VAEと同様に大きさは、傾向は捉えているものの、入力した通りに生成することはできませんでした。
カテゴリーデータとして与えたらもう少し変わるのかも知れません。
Diffusion Model
Diffusion Modelはランダムパラメータから徐々にノイズを除去して、欲しいデータを生成する方法です。
下図に出てくるDiffusion modelは全て同じものです。
いくつもモデルを作る必要はなく、ノイズを少しだけ除去するモデルに何度も通すことで、明瞭なデータを生成します。
ただし、どの段階のノイズを除去しているかが分かるように時間パラメータtもモデルに渡します。
モデルの学習は、教師データから①ノイズがa%のったデータと、②ノイズがb%のったデータを生成し、
①から②が生成できるようにモデルを学習させます。
ここで、a > bで、①の方がちょっとノイズが多くのっていて、②の方がより明瞭なデータになっています。
Diffusionモデルの基本についてはこちらを参考にさせていただきました。
英語ですが、非常に分かりやすく説明されています。
Diffusion Model
ノイズを少しだけ除去するモデルです。
画像の場合は、UNetを使う場合が多いようですが、今回は適当にMLPを複数回通します。
- モデルはDecoder, Generatorと似ています。
ただし、インプットは出力データと同じサイズになります。 - どのタイミングであるかの時間t、生成条件cもインプットになります。今回は単純に繋げてLinear層に通しました。
class DiffusionModel2(nn.Module):
def __init__(self, chs):
super().__init__()
ch = [20] + chs
self.diff = nn.Sequential()
for idx, (in_ch, out_ch) in enumerate(zip(ch[:-1], ch[1:])):
self.diff.add_module(f"linear_{idx:02d}", nn.Linear(in_ch, out_ch))
self.diff.add_module(f"bn_{idx:02d}", nn.BatchNorm1d(out_ch))
self.diff.add_module(f"relu_{idx:02d}", nn.ReLU(inplace=True))
self.out = nn.Linear(chs[-1] + 10, 10)
def forward(self, x, t, c):
x = x.reshape(-1, 10)
x = torch.cat([x] + [t]*5 + [c]*5, dim=1) # うまく生成できないので、tとcの影響を増やしたくてチャンネル数を増やしてみた。
x = self.diff(x)
x = torch.cat([x] + [t]*5 + [c]*5, dim=1)
x = self.out(x)
x = x.reshape(-1, 1, 2, 5)
return x
ノイズ生成
綺麗な学習データにノイズを付与することで、各タイミングでの学習データを準備します。
iteration毎にこの関数を利用して、特定割合のノイズを加えたデータx_t0と、x_t0よりちょっとだけノイズの少ないx_t1を作成して、学習データに使います。
class ForwardNoise:
def __init__(self, time_steps):
self.time_steps = time_steps
self.time_bar = 1 - torch.linspace(0, 1.0, time_steps + 1) # time_steps数分割した0~1の値(tensor)
self.time_bar = self.time_bar.reshape(-1, 1, 1, 1) # あとでxに足すので、次元数を合わせておく
def __call__(self, x):
# どの時刻を学習データにするかはランダムにきめる
ts = torch.randint(low=0, high=self.time_steps, size=(x.shape[0],))
noise = torch.randn(size=x.shape, device=x.device)
alpha_t0 = self.time_bar[ts]
alpha_t1 = self.time_bar[ts+1]
x_t0 = x * (1 - alpha_t0) + noise * alpha_t0 # alpha_t0の比率に応じてnoiseを加える
x_t1 = x * (1 - alpha_t1) + noise * alpha_t1 # x_t0よりちょっとだけnoiseが少ないデータ (教師データになる)
return x_t0, x_t1, alpha_t0.reshape(-1, 1)
生成関数
学習が終わって、いざ生成するときに使います。
ノイズをdiffusionモデルにtime_steps数回通すことでデータが生成されます。
for文で回すだけの単純な処理になります。
時刻情報を渡す必要があることは、忘れないようにご注意ください。
def predict(model, time_bar, x, c):
model.eval()
with torch.no_grad():
# 時間を適切な次元に変換するためのtensor
ones = torch.ones([x.shape[0], 1])
for t in time_bar:
x = model(x, ones*t.item(), c)
return x
動作確認
# test
ch = [4, 8, 4]
bs = 3
diffusion = DiffusionModel2(ch)
forward_noise = ForwardNoise(10)
x = torch.ones([bs, 1, 2, 5])
x0, x1, ts = forward_noise(x)
print(f"{x0.shape=}")
print(f"{torch.mean(x0)=}")
print(f"{x1.shape=}")
print(f"{torch.mean(x1)=}")
print(f"{ts.shape=}")
c = torch.ones([bs, 1]) * 0.5
y = diffusion(x0, ts, c)
print(y.shape)
学習関数
dataloaderから受け渡されたxにノイズを加えて、x_t0, x_t1を作成し、それを学習データとする処理が加わる以外は、回帰予測するAIと同じコードになります。
def diffusion_training(params):
dataloaders = create_dataloader(params.num_train_data, params.num_valid_data, params.batch_size)
diffusion_model = DiffusionModel2(params.chs)
forward_noise = ForwardNoise(params.time_steps)
optimizer = torch.optim.SGD(diffusion_model.parameters(), lr=params.lr)
optimizer.zero_grad()
loss_fn = torch.nn.MSELoss()
loss_logger = {"train": [], "valid": []}
log_dir = os.path.join("./", "log", params.task_name)
# 途中での確認用使う潜在変数と半径
sampling_z = torch.randn([9, 1, 2, 5])
sampling_r = torch.linspace(0.2, 1.0, 9).unsqueeze(1)
epoch_bar = tqdm(range(1, params.epochs+1))
for epoch in epoch_bar:
epoch_bar.set_description(f"Epoch:{epoch}")
loss_tmp = 0
iter_bar = tqdm(dataloaders["train"], leave=False)
diffusion_model.train()
for iter, (x, r) in enumerate(iter_bar):
# xにノイズを加えて学習データを作成する
x_t0, x_t1, t = forward_noise(x)
out = diffusion_model(x_t0, t, r)
loss = loss_fn(out, x_t1)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_tmp += loss.item()
loss_logger["train"].append(loss_tmp / (iter + 1))
loss_tmp = 0
iter_bar = tqdm(dataloaders["valid"], leave=False)
diffusion_model.eval()
for iter, (x, r) in enumerate(iter_bar):
x_t0, x_t1, t = forward_noise(x)
with torch.no_grad():
x_t0, x_t1, t = forward_noise(x)
out = diffusion_model(x_t0, t, r)
loss = loss_fn(out, x_t1)
loss_tmp += loss.item()
loss_logger["valid"].append(loss_tmp / (iter + 1))
epoch_bar.set_postfix({"loss=": f"{loss_logger['valid'][-1]:.2e}"})
save_loss_list_graph(log_dir, loss_logger)
if epoch % max(1, (int(params.epochs / params.img_save_steps))) == 0:
out = predict(diffusion_model, forward_noise.time_bar, sampling_z, sampling_r)
save_star_coord_graphs(log_dir, epoch, r=sampling_r, data1=out, s=2)
def training_log_settings(params):
# タスクの保存フォルダ
log_dir = os.path.join(r"./", "log", params.task_name)
os.makedirs(log_dir, exist_ok=True)
# epoch, iter毎のデータは多くなるので別フォルダを作る
log_dir_hist = os.path.join(log_dir, "hist", params.task_name)
os.makedirs(log_dir_hist, exist_ok=True)
# 設定ファイルの保存
with open(os.path.join(log_dir, "parameters.json"), 'w') as f:
json.dump(vars(params), f, indent=4)
def save_loss_list_graph(log_dir, loss_logger):
fig, ax = plt.subplots(1,1)
epoch = range(len(loss_logger["train"]))
ax.plot(epoch, loss_logger["train"], label="train")
ax.plot(epoch, loss_logger["valid"], label="valid")
ax.set_ylim(0, loss_logger["valid"][-1]*5)
ax.legend()
fig.savefig(os.path.join(log_dir, "loss_history.jpg"))
plt.clf()
plt.close()
ハイパーパラメーター
time_stepsを大きくしたら簡単に学習できるといわけではなさそうでした。
@dataclass
class HyperParameters:
task_name: str = "diffusion_01"
epochs: int = 5000
img_save_steps: int = 20
batch_size: int = 128
lr: float = 5e-2
num_train_data: int = 800
num_valid_data: int = 200
chs: list = field(default_factory=lambda: [16, 32, 64, 32, 16])
time_steps: int = 8
comment: str = ""
学習結果
loss推移
振動の大きい結果となりました。こんなものなのでしょうか?
生成データ
VAEやGANに比べると、星型が崩れてしまっていますが、生成することができました。
近年の流行りをみるに、上手に組めばもっと綺麗に生成できるのでしょうか?
おわりに
- たった10点のデータで、かつ学習データ数もたくさん準備できるので、簡単にモデルを学習できると思っていましたが、なかなかうまくいきませんでした。BatchNormのや学習率lrを適切に設定することの大切さと大変さを再確認できました。
- 複雑なプログラムを読むだけではなかなか理解することが難しいですが、簡易化して自分でモデル化することで、各モデルのプログラム構成を理解することができました。やはり自分で組んでみることが重要だと感じました。
免責
コピペ自由ですが、責任は負えませんのでご了承ください。














