特異値分解と縮約モデル

1. 目的と参考資料

こちらの論文に書かれている手法に興味があり、勉強した結果を整理しました。

流体解析に適用した事例
固有直行分解による流体解析: 1.基礎
衝突解析に適用した事例
Reduced ModelによるSUV側突時のセンターピラー変形モードの予測

参考にした記事等はこちらです。

web記事
- 主成分分析とは何かとその導出を丁寧に解説された記事
  主成分分析とは何なのか、とにかく全力でわかりやすく解説する
- 特異値分解とは何か丁寧に解説された記事
  特異値分解を詳しく解説
- 主成分分析の使い方例を紹介された記事
  主成分分析の使いみち
youtube
- 線形代数についての授業が受けられます
  予備校のノリで学ぶ「大学数学・物理」
  固有値、固有ベクトルは第12回「線形代数入門⑫ 固有値・固有ベクトル」

考え方を理解したくて、勉強中の内容をまとめました。
数学的に間違っている部分があるかもしれません。
間違いがあればコメント欄でご指摘お願いいたします。

2. 簡単な例で縮約モデルを作ってみる

題材とするデータと前処理

つくりたい縮約モデルは時系列データを予測するモデルです。
実際にはもっと複雑な現象を予測したいですが、簡単のため次のような解析データを予測することを考えます。

条件を変えて解析した結果が３つあるとします。
(事例は何でもいいのですが、例えば流体の解析をしたとして)
ある箇所の速度を時刻t=1,t=2計測した結果、次のようになっていたとします。

data No.	時刻t=1での値	時刻t=2での値
1	1	2
2	2	4
3	3	3

これをグラフにするとこんな感じ。
縮約モデルを考える場合には、もっとたくさんデータがあると思います。
今回は実際に手で計算することで理解する試みましたので、小さいデータ数としています。

これについて特異値分解をしていきますが、
data1の時刻t=1の値を$x_1$、時刻t=2の値の$y_1$と呼ぶことにします(私にとって分かりやすい記号にしただけです)。
また前準備として、x, yについて平均を差し引いておきます

data No.	x	y	x	y
1	$x_1 = 1$	$y_1 = 2$	$x_1 = -1$	$y_1 = -1$
2	$x_2 = 2$	$y_2 = 4$	$x_2 = 0$	$y_2 = 1$
3	$x_3 = 3$	$y_3 = 3$	$x_3 = 1$	$y_3 = 0$
mean	$\overline{x}=2$	$\overline{y}=3$	$\overline{x}=0$	$\overline{y}=0$

このデータを行列にします

A = \left(
\begin{array}{cc}
-1 & -1\\
0 & 1\\
1 & 0
\end{array}
\right)

特異値分解

準備ができたので、これを特異値分解していきます。
手順に従って計算していきます。なぜこれで分解できるのかは、上記のリンクを参照のこと。

計算式

$AA^T$の固有値と固有ベクトルを求めます ($ AA^TU=\lambda U $)

$AA^T$

AA^T = \left(
\begin{array}{cc}
-1 & -1\\
0 & 1\\
1 & 0
\end{array}
\right)
\left(
\begin{array}{ccc}
-1 & 0 & 1\\
-1 & 1 & 0\\
\end{array}
\right) = 
\left(
\begin{array}{ccc}
2 & -1 & -1\\
-1 & 1 & 0\\
-1 & 0 & 1\\
\end{array}
\right)

固有値

\left|
\begin{array}{ccc}
2-\lambda & -1 & -1\\
-1 & 1-\lambda & 0\\
-1 & 0 & 1-\lambda\\
\end{array}
\right| = 
(2-\lambda)(1-\lambda)^2 - (1-\lambda) - (1-\lambda)

 = (\lambda^2 - 3\lambda+2)(1-\lambda) - 2(1-\lambda) = (\lambda^2 -3\lambda)(1-\lambda) = \lambda(\lambda-3)(\lambda-1) = 0

\lambda = 3, 1, 0

固有ベクトルは

$\lambda = 3$のとき

\left(
\begin{array}{ccc}
2-\lambda & -1 & -1\\
-1 & 1-\lambda & 0\\
-1 & 0 & 1-\lambda\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
-1 & -1 & -1\\
-1 & -2 & 0\\
-1 & 0 & -2\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)=
\left(
\begin{array}{ccc}
0\\
0\\
0\\
\end{array}
\right)

\left\{
\begin{array}{lll}
-a-b-c=0\\
-a-2b=0\\
-a-2c=0
\\
\end{array}
\right.

u_1 = s_1
\left(
\begin{array}{ccc}
-2/\sqrt{6}\\
1/\sqrt{6}\\
1/\sqrt{6}\\
\end{array}
\right)

$\lambda = 1$のとき

\left(
\begin{array}{ccc}
2-\lambda & -1 & -1\\
-1 & 1-\lambda & 0\\
-1 & 0 & 1-\lambda\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
1 & -1 & -1\\
-1 & 0 & 0\\
-1 & 0 & 0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)=
\left(
\begin{array}{ccc}
0\\
0\\
0\\
\end{array}
\right)

\left\{
\begin{array}{lll}
a-b-c=0\\
a=0\\
a=0
\\
\end{array}
\right.

u_2 = s_2
\left(
\begin{array}{ccc}
0\\
-1/\sqrt{2}\\
1/\sqrt{2}\\
\end{array}
\right)

$\lambda = 0$のとき

\left(
\begin{array}{ccc}
2-\lambda & -1 & -1\\
-1 & 1-\lambda & 0\\
-1 & 0 & 1-\lambda\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
2 & -1 & -1\\
-1 & 1 & 0\\
-1 & 0 & 1\\
\end{array}
\right)
\left(
\begin{array}{ccc}
a\\
b\\
c\\
\end{array}
\right)=
\left(
\begin{array}{ccc}
0\\
0\\
0\\
\end{array}
\right)

\left\{
\begin{array}{lll}
2a-b-c=0\\
a-b=0\\
a-c=0
\\
\end{array}
\right.

u_3 = s_3
\left(
\begin{array}{ccc}
1/\sqrt{3}\\
1/\sqrt{3}\\
1/\sqrt{3}\\
\end{array}
\right)

続いて、$A$と$A^T$を入れ替えて$A^TA$の固有値と固有ベクトルを求めます ($ A^TAV=\lambda V $)

$A^TA$

A^TA = 
\left(
\begin{array}{ccc}
-1 & 0 & 1\\
-1 & 1 & 0\\
\end{array}
\right)
\left(
\begin{array}{cc}
-1 & -1\\
0 & 1\\
1 & 0
\end{array}
\right)
= 
\left(
\begin{array}{cc}
2 & 1 \\
1 & 2\\
\end{array}
\right)

固有値

\left|
\begin{array}{cc}
2-\lambda & 1\\
1 & 2-\lambda\\
\end{array}
\right| = 
(2-\lambda)^2 - 1 = \lambda^2 - 4\lambda + 3 = (\lambda-3)(\lambda-1)=0

\lambda = 3, 1

固有ベクトルは

$\lambda = 3$のとき

\left(
\begin{array}{ccc}
2-\lambda & 1\\
1 & 2-\lambda\\
\end{array}
\right)
\left(
\begin{array}{cc}
a\\
b\\
\end{array}
\right)
=
\left(
\begin{array}{cc}
-1 & 1\\
1 & -1\\
\end{array}
\right)
\left(
\begin{array}{cc}
a\\
b\\
\end{array}
\right)=
\left(
\begin{array}{cc}
0\\
0\\
\end{array}
\right)

\left\{
\begin{array}{ll}
-a+b=0\\
a-b=0\\
\end{array}
\right.

v_1 = t_1
\left(
\begin{array}{cc}
1/\sqrt{2}\\
1/\sqrt{2}\\
\end{array}
\right)

$\lambda = 1$のとき

\left(
\begin{array}{ccc}
2-\lambda & 1\\
1 & 2-\lambda\\
\end{array}
\right)
\left(
\begin{array}{cc}
a\\
b\\
\end{array}
\right)
=
\left(
\begin{array}{cc}
1 & 1\\
1 & 1\\
\end{array}
\right)
\left(
\begin{array}{cc}
a\\
b\\
\end{array}
\right)=
\left(
\begin{array}{cc}
0\\
0\\
\end{array}
\right)

\left\{
\begin{array}{ll}
a+b=0\\
a+b=0\\
\end{array}
\right.

v_2 = t_2
\left(
\begin{array}{cc}
1/\sqrt{2}\\
-1/\sqrt{2}\\
\end{array}
\right)

$AA^T$と$A^TA$の固有値と固有ベクトルが求まったので、　　

特異値分解の結果はこのようになります

A = U\Sigma V^T

\left(
\begin{array}{ccc}
-1 & -1\\
0 & 1\\
1 & 0\\
\end{array}
\right)
  = 
\left(
\begin{array}{ccc}
-2/\sqrt{6} & 0\\
1/\sqrt{6} & -1/\sqrt{2}\\
1/\sqrt{6} & 1/\sqrt{2}\\
\end{array}
\right)
\left(
\begin{array}{cc}
\sqrt{3} & 0\\
0 & \sqrt{1}\\
\end{array}
\right)
\left(
\begin{array}{cc}
1/\sqrt{2} & 1/\sqrt{2}\\
1/\sqrt{2} & -1/\sqrt{2}\\
\end{array}
\right)

特異値分解の解釈

ここでそれぞれの行列の意味について考えます。
一番右の$V$ですが、これは、$A^TA$の固有ベクトルでした($A^TAV = \lambda V$)。
行列Aは最初に平均を引いていましたが、その部分から$A^TA$を記述すると、

A^TA = 
\left(
\begin{array}{cc}
x_1 - \overline{x} & x_2 - \overline{x} & x_3 - \overline{x}\\
y_1 - \overline{y} & y_2 - \overline{y} & y_3 - \overline{y}\\
\end{array}
\right)
\left(
\begin{array}{ccc}
x_1 - \overline{x} & y_1 - \overline{y}\\
x_2 - \overline{x} & y_2 - \overline{y}\\
x_3 - \overline{x} & y_3 - \overline{y}
\end{array}
\right)

であるので、対象としているxyの分散共分散行列になります。
分散共分散行列の固有ベクトルは主成分分析の各軸を示すベクトルです（詳しくは参照リンクの主成分分析とは何かを参照）
ですのでVを図に示すと次のようになります。

ここで図は２通りで示します。
左は本記事の最初に示した図と同じで、横軸が時間で縦軸が求めたい値を示しています。
右側は時刻t1の値をx(横軸）として、時刻t2の値をy(縦軸）として示した図です（主成分分析で良く見る図は右側だと思います）。
（私は当初この２つの図が頭の中で繋がっておらず、なかなか理解ができませんでした）

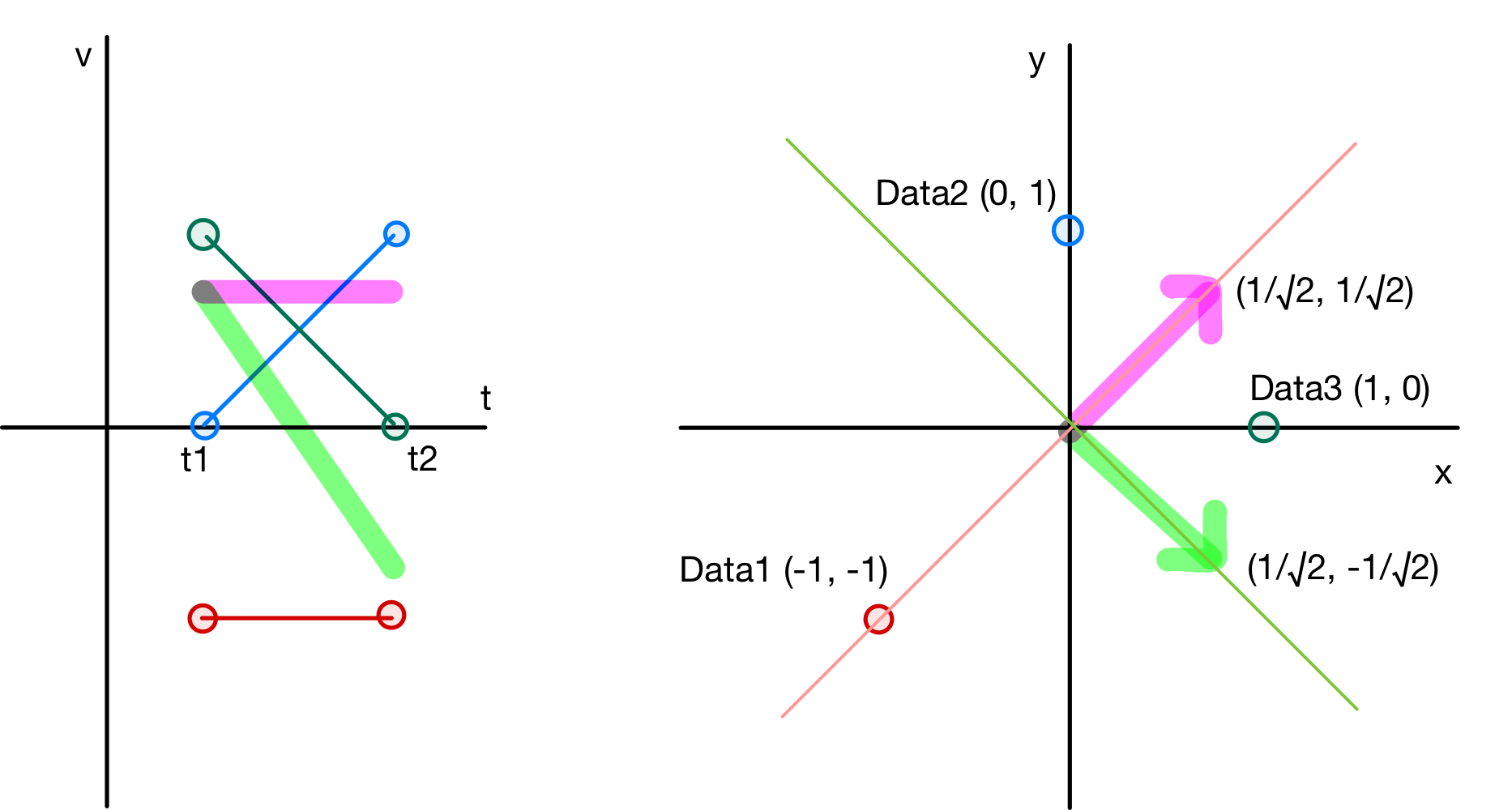
各赤、青、緑の◯は各データを示しており、ピンクと緑の蛍光色で示した線（図左）、ベクトル（右図）が行列Vを示しています。
今回の事例ではピンクの第1主成分がt1,t2の平均値を示しており、緑色の第２主成分がt1とt2にどれだけ差があるかを示しています。
そして、第1主成分と第2主成分の重要性を示しているのが、特異値分解で出てきた$\Sigma$です。
$\Sigma V^T$を計算すると、主成分の重要性も含めたベクトルが得られます。

\Sigma V^T = 
\left(
\begin{array}{cc}
\sqrt{3} & 0\\
0 & \sqrt{1}\\
\end{array}
\right)
\left(
\begin{array}{cc}
1/\sqrt{2} & 1/\sqrt{2}\\
1/\sqrt{2} & -1/\sqrt{2}\\
\end{array}
\right) = 
\left(
\begin{array}{cc}
\sqrt{3}/\sqrt{2} & \sqrt{3}/\sqrt{2}\\
1/\sqrt{2} & -1/\sqrt{2}\\
\end{array}
\right)

主成分のベクトルを$V^T$から$\Sigma V^T$に置き換えた図がこちらになります。

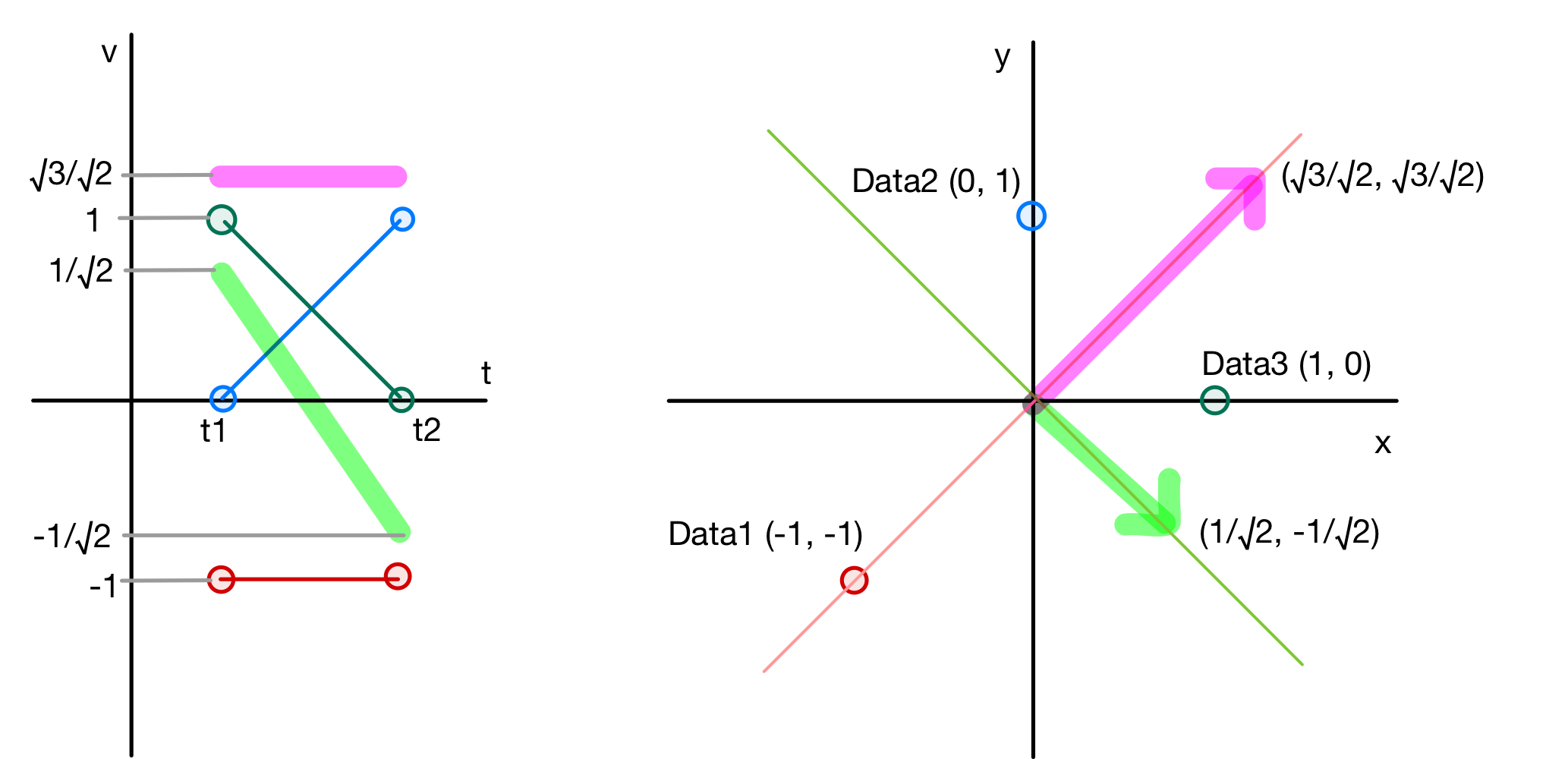
今回はどちらの情報（軸）も重要なのであまり見た目が変わりませんが、必要性の低い情報についてはベクトルが小さくなります。
必要性の低い情報を削除することで次元削減が可能となります。
今回は少ないデータ点数でしたが、通常縮約モデルを検討したい事例ではデータ数が非常に大きくなるため、次元削減が重要となります。
＊　次元数は最初の行列AのRankで決まります。同じ結果が含まれないようにデータを準備できていれば、データ数と時間刻みの小さい方の数だけ次元が現れます。

そして、最後に行列Uは主成分から元のデータに戻すための値になります。
data1を復元した場合はこちらです。

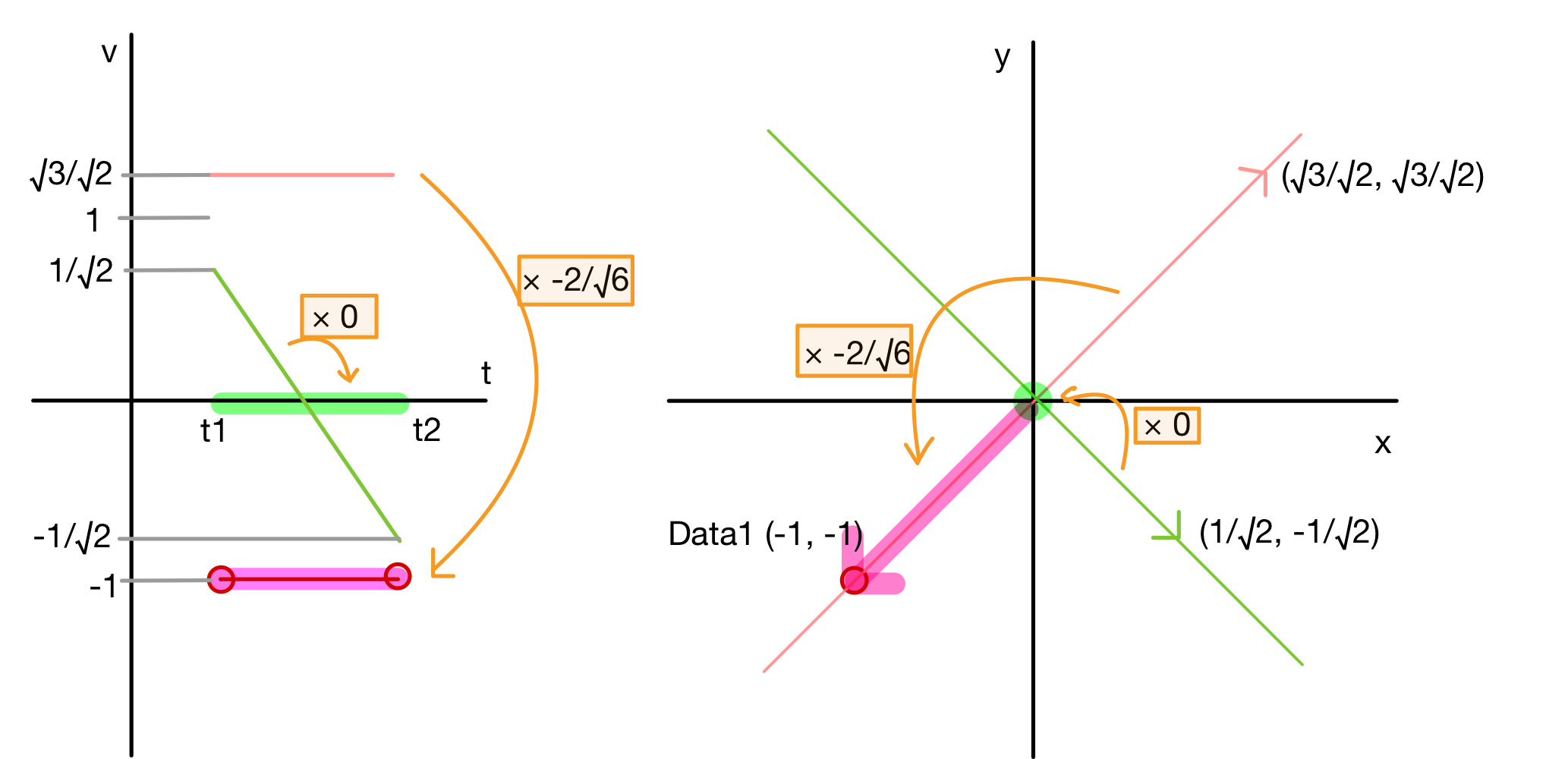
t1,t2の平均値を示す第1主成分を$-2/\sqrt{6}$倍して、第2主成分は0倍して足し合わせると元のデータが復元できます。
同様にdata2を復元すると、下の図のようになります。

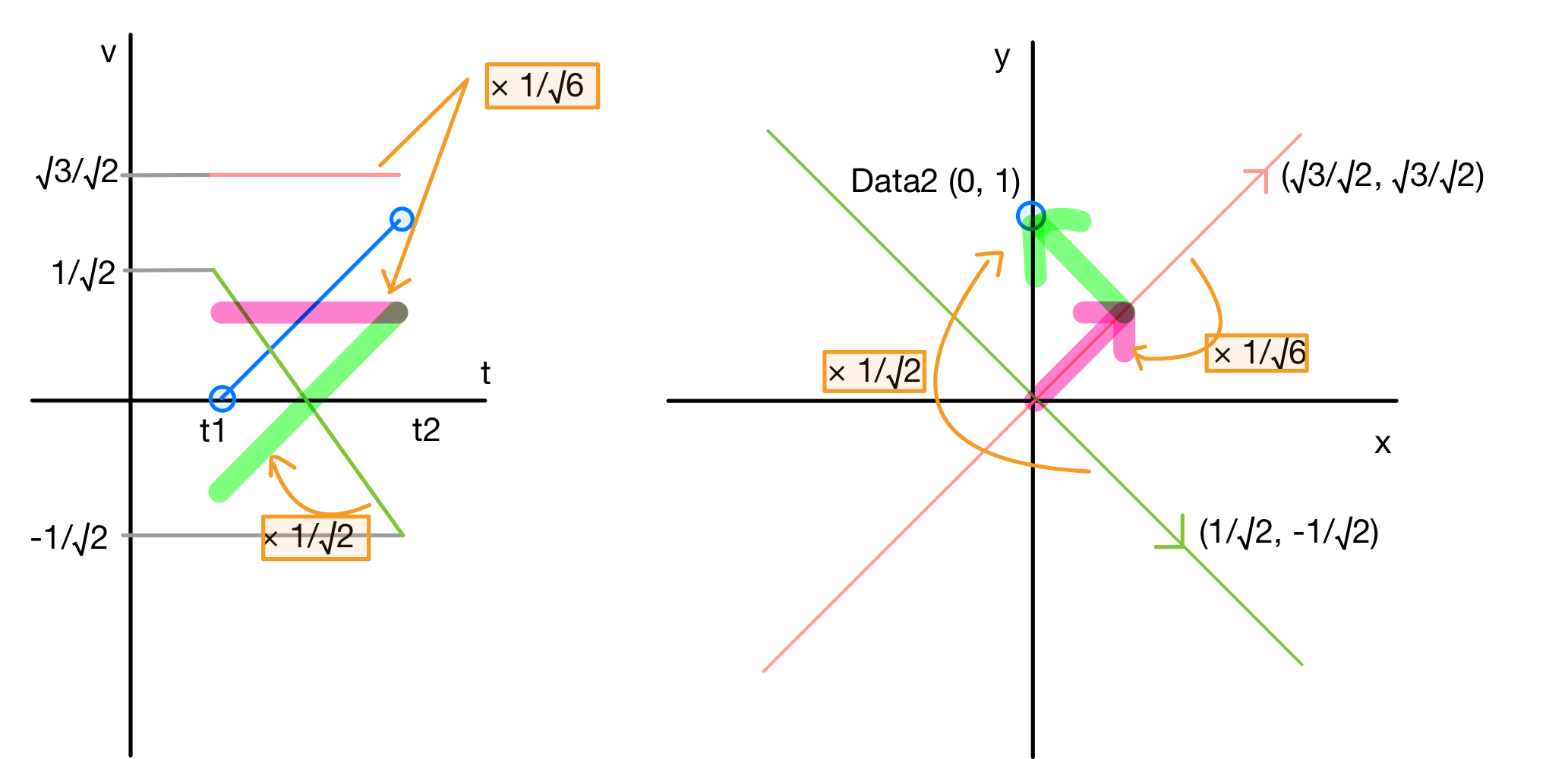
縮約モデル(Reduced Orrder Model)

最後にこれをReduced Order Modelと利用する方法です。
Aが求めたい結果ですので、Aを$(x_i, y_i)$としてこれを求める式とします。

A = U\Sigma V^T

\left(
\begin{array}{c}
x_i & y_i\\
\end{array}
\right)
  = 
\left(
\begin{array}{ccc}
p1_i & p2_i\\
\end{array}
\right)
\left(
\begin{array}{cc}
\sqrt{3} & 0\\
0 & \sqrt{1}\\
\end{array}
\right)
\left(
\begin{array}{cc}
1/\sqrt{2} & 1/\sqrt{2}\\
1/\sqrt{2} & -1/\sqrt{2}\\
\end{array}
\right)

解析条件からこのpを求める近似式を別途作成することで、特異値分解を利用した予測モデルが完成します。
（求まるのは平均値$(\overline{x}, \overline{y})$を引いた値ですので、最後に平均値を加える必要があります）
必要に応じて、次元を削減することで予測するパラメータ数を減らすことができます。

3. 縮約モデルを試してみる

実際の使い方を試してみたいと思います。

pythonのコードは特異値分解を詳しく解説に書かれているコードを参考にさせていただきました。
事例はフィクションです。

題材

きゃべつくんは、ハンバーグが大好きです。
いつも美味しく作ることができるのですが、見た目が綺麗ではありません。
そこで、見た目が綺麗なハンバーグを作成するために、肉の量、こねる回数、形を整えるために叩く回数を変えてハンバーグを8個作りました。

	肉の量 ×10[g]	こねる回数[回]	叩く回数[回]
1	1	1	1
2	1	3	2
3	1	2	3
4	2	3	1
5	2	2	2
6	2	1	3
7	3	1	1
8	3	3	2

そして出来上がったハンバーグを半分に切って、断面の形状を記録しました。

断面はどれも山型になっています。
そこで各計測点ごとの平均と（下左図）、各ハンバーグの平均からの差(下右図）を求めてグラフにしてみました。
平均をみると、全体的には山型でありながら、左側が出っ張り、真ん中が凹んでいることがわかります。

それでは、肉の量などのパラメータから肉の断面を求める予測式を作りたいと思います。
全体的に山型になることはもうわかっているので、山型を予測する式を計算する必要はありません。
ですので、不必要な情報が削ぎ落とされた上図右の”平均からの差分”を予測することを考えます。

平均からの差分(上右図）を行列にして、特異値分解します。

import numpy as np
from numpy.linalg import svd

# 平均からの差分をnumpy配列にする
yn = [[0.0, -3.9375, -7.875, -10.875, -2.6875, -0.5, -6.5, -3.5, -3.5, -1.75, 0.0],
      [0.0, -1.4375, -2.875,   0.125, -6.1875, -6.5, -0.5, -3.5, -3.5, -1.75, 0.0],
      [0.0,  1.0625,  2.125,   2.125, -0.6875, -3.5, -3.5, -3.5, -3.5, -1.75, 0.0],
      [0.0, -1.9375, -3.875,  -0.875, -4.6875, -2.5,  3.5,  0.5,  0.5,  0.25, 0.0],
      [0.0,  0.5625,  1.125,   1.125,  0.8125,  0.5,  0.5,  0.5,  0.5,  0.25, 0.0],
      [0.0,  3.0625,  6.125,   3.125,  6.3125,  3.5, -2.5,  0.5,  0.5,  0.25, 0.0],
      [0.0,  0.0625,  0.125,  -2.875,  5.3125,  7.5,  1.5,  4.5,  4.5,  2.25, 0.0],
      [0.0,  2.5625,  5.125,   8.125,  1.8125,  1.5,  7.5,  4.5,  4.5,  2.25, 0.0],]
yn = np.array(yn)

# svd()で特異値分解を実行
u, sigma, vt = svd(yn)

行列式にするとこんな感じ

y_n = U\Sigma V^T

\left(
\begin{array}{ccccccccccc}
0.0&-3.9375&-7.875&-10.875&-2.6875&-0.5&-6.5&-3.5&-3.5&-1.75&0.0\\
0.0&-1.4375&-2.875&  0.125&-6.1875&-6.5&-0.5&-3.5&-3.5&-1.75&0.0\\
0.0& 1.0625& 2.125&  2.125&-0.6875&-3.5&-3.5&-3.5&-3.5&-1.75&0.0\\
0.0&-1.9375&-3.875& -0.875&-4.6875&-2.5& 3.5& 0.5& 0.5& 0.25&0.0\\
0.0& 0.5625& 1.125&  1.125& 0.8125& 0.5& 0.5& 0.5& 0.5& 0.25&0.0\\
0.0& 3.0625& 6.125&  3.125& 6.3125& 3.5&-2.5& 0.5& 0.5& 0.25&0.0\\
0.0& 0.0625& 0.125& -2.875& 5.3125& 7.5& 1.5& 4.5& 4.5& 2.25&0.0\\
0.0& 2.5625& 5.125&  8.125& 1.8125& 1.5& 7.5& 4.5& 4.5& 2.25&0.0\\
\end{array}
\right)
=
\left(
\begin{array}{ccccccccccc}
 0.62& -0.44& -0.  &  0.32& -0.49& -0.16& -0.23&  0.  \\
 0.34&  0.45&  0.05&  0.57&  0.53& -0.15& -0.2 & -0.06\\
 0.11&  0.28& -0.5 &  0.11& -0.2 &  0.68& -0.15&  0.34\\
 0.15&  0.18&  0.52& -0.45& -0.01&  0.15& -0.66&  0.11\\
-0.09&  0.01& -0.03& -0.  &  0.03& -0.44&  0.01&  0.89\\
-0.32& -0.16& -0.58& -0.05&  0.11& -0.3 & -0.63& -0.2 \\
-0.27& -0.62&  0.24&  0.34&  0.38&  0.41& -0.15&  0.18\\
-0.54&  0.28&  0.29&  0.49& -0.52& -0.06& -0.16& -0.05\\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
24.45&  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  & 15.4&   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &  12.12 & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
 0.  &  0. &   0.   & 0.  &  0. &   0.&    0.&    0.\\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
-0.  & -0.23& -0.45& -0.46& -0.37& -0.3 & -0.32& -0.31& -0.31& -0.15&  0.\\  
 0.  &  0.08&  0.16&  0.58& -0.42& -0.58&  0.25& -0.16& -0.16& -0.08&  0.\\  
 0.  & -0.21& -0.43& -0.13& -0.35&  0.03&  0.62&  0.33&  0.33&  0.16&  0.\\  
-0.21& -0.92&  0.26&  0.14&  0.12&  0.  & -0.02& -0.02& -0.02& -0.01&  0.\\  
-0.47&  0.09& -0.06&  0.22& -0.41&  0.67&  0.03& -0.22& -0.22& -0.11&  0.\\  
 0.83& -0.16&  0.2 &  0.  & -0.24&  0.35&  0.11& -0.15& -0.15& -0.08&  0.\\  
 0.07& -0.04&  0.06&  0.19& -0.47&  0.02& -0.64&  0.38&  0.38&  0.19&  0.\\  
-0.2 &  0.1 &  0.69& -0.57& -0.33& -0.08&  0.16&  0.04&  0.04&  0.02&  0.\\  
 0.  & -0.  &  0.  & -0.  & -0.  & -0.  & -0.  & -0.67&  0.73& -0.13&  0.\\  
-0.  &  0.  &  0.  & -0.  & -0.  & -0.  &  0.  & -0.33& -0.13&  0.93&  0.\\  
 0.  &  0.  &  0.  &  0.  &  0.  &  0.  &  0.  &  0.  &  0.  &  0.  &  1.\\  
\end{array}
\right)

特異値分解で得られた固有ベクトル$V^T$をグラフにします。

図の左に$V^T$、右に特異値（重要度）を掛け合わせた$\Sigma V^T$を示します。

$\Sigma V^T$をみると、v3~v7は値がほぼ0であり、これらの項は無視してしまっても問題ないことがわかります。
ですので、上位３つの固有ベクトルv0~v2のみに絞ってグラフ化します。

このグラフを見て分析をしてもいいのですが、最初に求めた平均値に対して、どのように作用するのかを確認した方が分かりやすいと思います。
下のグラフは、固有ベクトルv0,v1,v2それぞれの影響を示したグラフです。

赤線は実際に作ったハンバーグの平均断面、水色線は平均から$\Sigma V^T$引いた断面、緑色線は平均に$\Sigma V^T$を加えた断面です。
左がv0、真ん中がv1、右がv2の影響をそれぞれ示しています。

このグラフをみるとそれぞれの固有ベクトルは次の影響をもっていそうです。

$V^T$	影響
$v_0$	全体的な断面の大きさを変える
$v_1$	x=10~35の範囲に見られるギザギザの大きさを変える
$v_2$	x=30付近の断面の大きさを変える

つまり、ハンバーグを作るときに変えたパラメータは、単独でもしくは相互作用によって、
出来上がり断面にこれらの影響を与えています。

それぞれの固有ベクトルの影響を考察してみましたが、分析をしなくても縮約モデルは機械的に作ることができます。
ということで、縮約モデルの作成に戻りたいと思います。

$\Sigma V^T$のベクトルに係数をかけて足し合わせることで、元のグラフを再現できるのでした。
それを確認してみます。

3個目のハンバーグの形状を固有ベクトルの足し合わせで再現できるかを確認してみます。
固有ベクトルにかける係数は特異値分解で得られた行列uの3行目です。
行列式にするとこうなります。

\left(
\begin{array}{ccccccccccc}
0.0& 1.0625& 2.125&  2.125&-0.6875&-3.5&-3.5&-3.5&-3.5&-1.75&0.0\\
\end{array}
\right)
=
\left(
\begin{array}{ccccccccccc}
 0.11&  0.28& -0.5\\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
24.45&  0. &   0.   \\
 0.  & 15.4&   0.   \\
 0.  &  0. &  12.12 \\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
-0.  & -0.23& -0.45& -0.46& -0.37& -0.3 & -0.32& -0.31& -0.31& -0.15&  0.\\  
 0.  &  0.08&  0.16&  0.58& -0.42& -0.58&  0.25& -0.16& -0.16& -0.08&  0.\\  
 0.  & -0.21& -0.43& -0.13& -0.35&  0.03&  0.62&  0.33&  0.33&  0.16&  0.\\  
\end{array}
\right)

この結果をグラフ化した図が、こちらの9個並んでいるグラフの右上のグラフです。
赤色が実物を計測したデータで、青い破線が固有ベクトルに係数を欠けて足し合わせることで再現した結果です。
赤線と青線は重なっており、問題なく再現できていることがわかります。

今回は上位3つの固有ベクトルを足し合わせて断面形状の再現をしていますが、もっと少なくしたり、全部使って再現した場合はどうでしょうか？
それを説明しているのが残りのグラフです。
左上は一番目の固有ベクトルのみで再現した場合、以降固有ベクトル2つで、３つで・・・再現した場合を順番に並べています。
求める精度によりますが、固有ベクトル１つ、２つでは予測から少し外れているますが、3つ以降はほとんど変わらないことがわかります。

すでにある断面形状を再現していましたが、新しい条件で作ったハンバーグの断面形状を予測するには、次式の$P_1,P_2,P_3$が必要になります。ですので、パラメータからPを求めれば良いことになります。
断面図は11ヶ所の計測データからなるので、11点を予測しなければなりませんが、特異値分解をして不要な固有ベクトルを落とすことで、予測しなければならないパラメータが3になりました。

Y =
\left(
\begin{array}{ccccccccccc}
 P_1 &  P_2 & P_3\\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
24.45&  0. &   0.   \\
 0.  & 15.4&   0.   \\
 0.  &  0. &  12.12 \\
\end{array}
\right)
\left(
\begin{array}{ccccccccccc}
-0.  & -0.23& -0.45& -0.46& -0.37& -0.3 & -0.32& -0.31& -0.31& -0.15&  0.\\  
 0.  &  0.08&  0.16&  0.58& -0.42& -0.58&  0.25& -0.16& -0.16& -0.08&  0.\\  
 0.  & -0.21& -0.43& -0.13& -0.35&  0.03&  0.62&  0.33&  0.33&  0.16&  0.\\  
\end{array}
\right)

今回は、線形回帰でパラメータを予測してみたいと思います。
予測に使うインプットはxは肉の量、こねる回数、叩く回数で、教師データは特異値分解で得られた$u$です。

from sklearn.linear_model import LinearRegression

# xは肉の量、こねる回数、叩く回数
X_train = test_parameters
# yは特異値分解で得られた係数。
# 上位3つの主成分の係数だけ予測すればいいのでスライスしている
y_train = u[:, :3]

lr = LinearRegression()
lr.fit(X_train, y_train)

これで回帰式ができました。
あとはこれをつなげてあげれば縮約モデルの完成です。

# 肉の量=3、こねる回数=0、叩く回数=0
parameters = np.array([[3, 0, 0]])
# 縮約モデル
new_section = lr.predict(parameters) @ np.diag(s[:3]) @ vt[:3, :] + y_mean

# グラフ化
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,1, figsize=(6,4))
ax.plot(x0, new_section[0], c="red")
ax.grid(lw=1)
ax.set_xlabel("width")
ax.set_ylabel("height")
ax.set_ylim(0, 40)
plt.show()
plt.clf()
plt.close()

この縮約モデルを使って検討することで、無事に綺麗な形状のハンバーグを作ることができました。

おわりに

題材は少し無理のある内容であったかも知れませんが、具体例を用いて縮約モデルを説明してみました。
少しでも参考になれば幸いです。

特異値分解による縮約モデル(Reduced Order Model)について