pythonではじめるデータ分析 (データ前処理〜機械学習)

はじめに

初心者向けにpythonでのデータ前処理から機械学習モデル構築までを解説したいと思います。
機械学習には勾配ブースティングを使用します。

ソースコード
https://gitlab.com/ceml/qiita/-/blob/master/src/python/notebook/first_time_ml.ipynb

本記事の内容

目次

1．データの前処理
　　1-1．データの読み込み
　　1-2．データの結合
　　1-3．欠損地補完
　　1-4．特徴量作成
　　1-5．データ分割
2．機械学習
　　2-1．データセット作成とモデルの定義
　　2-2．モデルの訓練と評価
　　2-3．特徴量の重要度を確認

データセットについて

・提供元：カルフォルニア工科大学
・内容：心臓病患者の検査データ
・URL :https://archive.ics.uci.edu/ml/datasets/Heart+Disease
・上記URLにあるprocessed.cleveland.data, reprocessed.hungarian.data, reprocessed.hungarian.data, processed.switzerland

※　データのダウンロードは以下参照
pythonではじめるデータ分析 (データの可視化1)
https://qiita.com/CEML/items/d673713e25242e6b4cdb

解析目的

データセットは患者の病態を5つのクラスに分類しています。
この5つのクラスを機械学習に予測させます。
機械学習モデルは勾配ブースティングを使用します。

1. データ前処理

1.1 データの読み込み

import pandas as pd

columns_name = ["age", "sex", "cp", "trestbps", "chol", "fbs", "restecg", "thalach", "exang", "oldpeak","slope","ca","thal","class"]

cleveland = pd.read_csv("/Users/processed.cleveland.data",header=None, names=columns_name)
hungarian = pd.read_csv("/Users/reprocessed.hungarian.data",sep=' ',header=None, names=columns_name)
va = pd.read_csv("/Users/processed.va.data",header=None, names=columns_name)
switzerland = pd.read_csv("/Users/processed.switzerland.data",sep=",",header=None, names=columns_name)

hubgarianとswitzerlandで引数に与えているsepは文字区切りです。
この二つのデータは一つのカラムに全てのデータが入ってしまっているので，sepでカラム毎に切り分けています。
※　カラムの詳細はデータダウンロード参照記事を参照してください。

1-2. データの結合

全てのデータを結合して一括で扱えるようにします。

merge_data = pd.concat([cleveland,hungarian,va,switzerland],axis=0)
print(merge_data.shape)

# output
'''(921, 14)'''

1-3. 欠損地補完

このデータには欠損部に'？'が入力されているので，nullに変換し、その後データを数値型に変換します。
今回は勾配ブースティングを使用するのでnull値は変換せずにそのまま使用しますが、他のモデルであればnullをなんらかの数値に置換しなければなりません。

merge_data.replace({"?":np.nan},inplace=True)
merge_data = merge_data.astype("float")

# クラスが欠損している行を削除
merge_data.dropna(subset=["class"], inplace=True)

# 欠損値確認
print(merge_data.isnull().sum())

# output
''' 
age           0
sex           0
cp            0
trestbps     58
chol          7
fbs          82
restecg       1
thalach      54
exang        54
oldpeak      62
slope       119
ca          320
thal        220
class         0
dtype: int64 
'''

1-4. 特徴量作成

特徴量から新たな特徴量を作成するステップです。
通常まずこのステップは飛ばして、集めたデータだけを使用してモデルを作るかと思います。
そこでの精度をベースとして，精度向上のために新たな特徴量を作ります。
今回はチュートリアルという事で最初から作成してみます。
例として、平均年齢からの差分を特徴量として作成します。

merge_data['diff_age'] = merge_data['age'] - merge_data['age'].mean()

1-5. データ分割

データをtrain, test, validationの3つに分割します。
この時注意しなければならないのが、病態クラスは不均衡であるという点です。
具体的にみていきます。

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

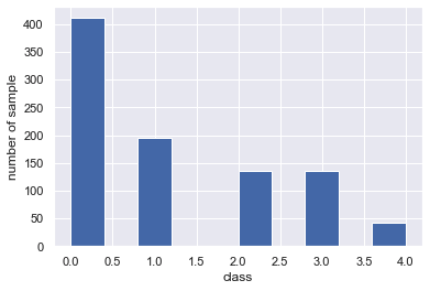
merge_data["class"].hist()
plt.xlabel("class")
plt.ylabel("number of sample")

健常者の0クラスが多く、病態の重い患者は少なくなっています。
現実問題においてこのような不均衡問題はとても多いです。

この割合を変えずにデータを分割する必要があります。

from sklearn.model_selection import StratifiedShuffleSplit

# 目的変数を分離
X = merge_data.drop("class",axis=1).values
y = merge_data["class"].values
columns_name = merge_data.drop("class",axis=1).columns

# 分類するための関数を定義
sss = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=0) 
def data_split(X,y):
    for train_index, test_index in sss.split(X, y):
        X_train, X_test = X[train_index], X[test_index]
        y_train, y_test = y[train_index], y[test_index]
    
    X_train = pd.DataFrame(X_train, columns=columns_name)
    X_test = pd.DataFrame(X_test, columns=columns_name)
    
    return X_train, y_train, X_test, y_test

# train, test, valに分離
X_train, y_train, X_test, y_test = data_split(X, y)
X_train, y_train, X_val, y_val = data_split(X_train.values, y_train)

# shape 確認
print("train shape", X_train.shape)
print("test shape", X_test.shape)
print("validation shape", X_val.shape)

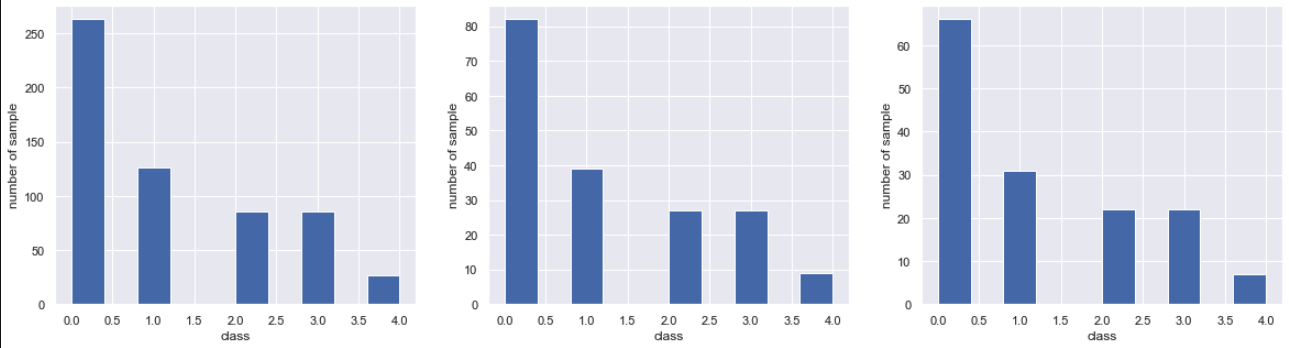
# クラスの割合を確認
plt.figure(figsize=(20,5))
plt.subplot(1,3,1)
plt.hist(y_train)

plt.subplot(1,3,2)
plt.hist(y_test)

plt.subplot(1,3,3)
plt.hist(y_val)

# output
'''
train shape (588, 14)
test shape (184, 14)
validation shape (148, 14)
'''

割合を変えずに分割出来ています。

2. 機械学習

2.1 データセット作成とモデルの定義

データセットを作成して、パラメータを与えます。

import lightgbm as lgb

# データセットを作成
train = lgb.Dataset(X_train, label=y_train)
valid = lgb.Dataset(X_val, label=y_val)

# モデルのパラメータを設定
params = {
    'reg_lambda' : 0.2,
    'objective': 'multiclass',
    'metric': 'multi_logloss',
    'num_class': 5,
    'reg_alpha': 0.1,
    'min_data_leaf': 100,
    'learning_rate': 0.025,
#     'feature_fraction': 0.8,
#     'bagging_fraction': 0.8
}

2.2 モデルの訓練と評価

モデル訓練時にはアーリーストッピングを指定して、ロスが下がらなくなったところで学習をストップします。
予測はargmaxで最尤をとります。
評価は混合行列とkappa係数により評価します。
クロスバリデーションは行わずホールドアウト検証のみ行います。

# 　モデルを訓練
model = lgb.train(params,
                  train,
                  valid_sets=valid,
                  num_boost_round=5000,
                  early_stopping_rounds=500)

# 予測
y_pred = model.predict(X_test, num_iteration=model.best_iteration)
y_pred = np.argmax(y_pred, axis=1)

# --------------------------モデルの評価-----------------------------------------------
from sklearn.metrics import confusion_matrix
from sklearn.metrics import cohen_kappa_score

# 混合行列を作成
result_matrix = pd.DataFrame(confusion_matrix(y_test,y_pred))
# クラス毎の正解率を計算
class_accuracy = [(result_matrix[i][i]/result_matrix[i].sum())*1 for i in range(len(result_matrix))]
result_matrix[5] = class_accuracy
# kappa係数を計算
kappa = cohen_kappa_score(y_test,y_pred)
print("kappa score:",kappa)

# plot
plt.figure(figsize=(7,5))
sns.heatmap(result_matrix,annot=True,cmap="Blues",cbar=False)
plt.xticks([5.5,4.5,3.5,2.5,1.5,0.5], ["accuracy",4, 3, 2, 1,0])
plt.ylabel('Truth',fontsize=13)
plt.xlabel('Prediction',fontsize=13)
plt.tick_params(labelsize = 13)

# output
'''
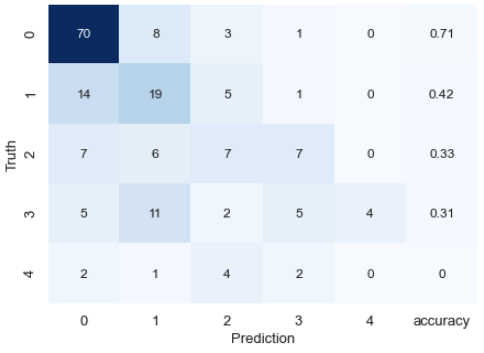
kappa score: 0.3368649587494572
'''

結果はあまり良くないですが、それはさておき、特徴量の重要度を確認します。

2-3. 特徴量の重要度を確認

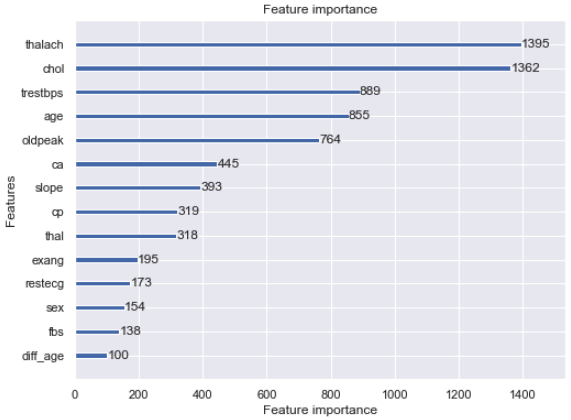
lgb.plot_importance(model, figsize=(8, 6))
plt.show()

まさかの作成した特徴量が最も低いという結果でした。

おわりに

今回はデータの前処理からホールドアウトによるモデルの評価までを行いました。
より精度を向上させるためには特徴量エンジニアリングや、ハイパラメータの検索が必要です。
また、精度を担保するためにはクロスバリデーションによる評価が必要になってきます。