LoginSignup
0
1
@C5D5E5

TensorFlow.NETとC#で「ディープラーニングを実装から学ぶ」(by @Nezuraさん)を追体験する

Posted at

はじめに

機械学習を学ぶにあたり、お伴の言語にはPythonを選択する方が多いと思います。しかし、C#のほうが手に馴染む、実装が頭に浮かびやすい、という方もいるはず。そのようなひとりとして、Qiitaの良記事について、C#で追体験を試みます。

# コードはやっつけの実装も多いのでご容赦を。

取り上げるのは、@Nezuraさんの「ディープラーニングを実装から学ぶ」の一連の記事です。

応用を第一に考えるならば、学習の仕組みはどうなっているのか、といった中身の話は飛ばしてもいいのかもしれませんが、中の仕掛けがどうしても気になる、自分なりに学習の仕組みに手を入れてみたい、という向きには、大変勉強になります。ありがとうございます。

本稿では、「ディープラーニングを実装から学ぶ(4-2) 学習(誤差逆伝播法2)」までの実装を目指します。一部、(誤差逆伝播法)での実装を含みます。

結論の先取り

  • PyThonでの実装に比べかなり実行時間はかかります。NumPyは補助的な実装であり性能面での不利があります。
  • 未実装のNumPyの機能を別途作り込む必要があります。
  • 行列を意識して記述する必要があります。
  • 数値型を意識して記述する必要があります。
  • とはいえ、実行速度、追加実装の負担は、動作確認に堪えられないほどではないと思います。
  • 動作確認後は、TensorFlow.NETに実装済みの高速な処理の活用が考えられます。

TensorFlow.NET

先の記事でも処理の中心は、Pythonの科学技術計算ライブラリNumPyを用いて記述されています。これらをC#で追体験するにあたり、NumPyのサブセットが実装されているTensorFlow.NETを利用します。

本稿で利用する環境

  • TensorFlow.NETのバージョン: 0.150.0
  • アプリケーションの種類: コンソールアプリケーション
  • ターゲットフレープワーク: .NET8.0
  • 浮動小数点数の型: float

main処理

以降、便宜上、class分けした単位で処理の実際を示します。methodの単位は、元のPythonの実装にほぼ従います。

Program.cs
using Tensorflow;
using Tensorflow.NumPy;
using static Tensorflow.Binding;

冒頭にusingでこの3つを指定します。2つめはnp(numpy)を利用するためのもの、3つめはtf(Tensor)を利用するためのもの。

Program.cs
static void Main(String[] args)
{
    String MNIST_Path = "d:\\mnist\\";

    NDArray trainData;
    NDArray trainLabel;
    NDArray testData;
    NDArray testLabel;

    (trainData, trainLabel, testData, testLabel) = MNISTManager.Load_MNIST(MNIST_Path);

    Attempt6(trainData, trainLabel, testData, testLabel);
}

MNISTの各種データは、Dドライブのmnistフォルダに置いています。
Load_MNISTは、MNISTデータをNDArrayに読み込んで返します。
Attempt6が処理の本体です。

# method名の後ろに数字が付いているのは、単に試行錯誤の跡です。

  • 入力層、中間層、出力層、トレーニング、の各部をclassとして実装しています。
  • トレーニング部は重み付け変数とバイアス変数をclass変数として持ち、インスタンス生成して、学習過程での変化を保持します。
  • 他classのmethodは、static呼び出しなので、インスタンス生成を行っていません。
Program.cs
// back propagation optimized
static void Attempt6(NDArray trainData, NDArray trainLabel, NDArray testData, NDArray testLabel)
{
    int d0 = 784;   // input
    int d1 = 50;    // middle layer 1
    int d2 = 100;   // middle layer 2
    int d3 = 10;    // output

    NDArray W1 = OutputLayer.He_Normal(d0, d1);
    NDArray b1 = np.zeros(d1, TF_DataType.TF_FLOAT).reshape((1, d1));
    NDArray W2 = OutputLayer.He_Normal(d1, d2);
    NDArray b2 = np.zeros(d2, TF_DataType.TF_FLOAT).reshape((1, d2));
    NDArray W3 = OutputLayer.He_Normal(d2, d3);
    NDArray b3 = np.zeros(d3, TF_DataType.TF_FLOAT).reshape((1, d3));

    int batch_size = 100;

    // input
    NDArray z0train = InputLayer.Init_Func(trainData);
    NDArray z0test = InputLayer.Init_Func(testData);

    // shuffle
    (NDArray z0, NDArray t) = Common.ShuffleData(z0train, trainLabel);

    // training
    Training training = new Training(W1, W2, W3, b1, b2, b3);

    NDArray y;
    NDArray yt;
    y = training.Propagation3(z0);
    yt = training.Propagation3(z0test);

    // print accuracy
    float accTrain;
    float accTest;
    accTrain = Training.Accuracy_Rate(y, t);
    accTest = Training.Accuracy_Rate(yt, testLabel);
    Console.WriteLine(String.Format(" accuracy of training data: {0:F6}", accTrain));
    Console.WriteLine(String.Format(" accuracy of test data:     {0:F6}", accTest));

    for (int i = 0; i < z0.shape[0]; i += batch_size)
    {
        Slice slice = new Slice(String.Format("{0}:{1}", i, i + batch_size));
        // Slice[] slices = Slice.ParseSlices(String.Format("{0}:{1}", i, i + batch_size));

        NDArray z0b = z0[slice];
        NDArray t0b = t[slice];

        // propagation and calc gradients
        training.PropagationAndCalcGradient_wo_Calc(z0b, t0b);

        y = training.Propagation3(z0);
        yt = training.Propagation3(z0test);

        // print accuracy
        accTrain = Training.Accuracy_Rate(y, t);
        accTest = Training.Accuracy_Rate(yt, testLabel);
        Console.WriteLine("No.{0}..{1}", i + 1, i + batch_size);
        Console.WriteLine(String.Format(" accuracy of training data: {0:F6}", accTrain));
        Console.WriteLine(String.Format(" accuracy of test data:     {0:F6}", accTest));
    }
}

最初に重み付け変数とバイアス編集を初期化します。次に学習データを正規化し、乱数で並び替えます。
一回トレーニングを行い、未学習状態での正答率を求めます。
その後、forループで100件ずつ学習を進め、正答率の変化を見ます。

  • 100件ずつデータ(NDArray)を区切る部分ですが、Sliceを用いてPythonの表記の流儀を持ち込んでいます。

入力層

InputLayer.cs
public static NDArray Init_Func(NDArray x)
{
    return Min_Max(x);
    // return Z_Score(x);
}

public static NDArray Min_Max(NDArray x)
{
    NDArray x_min = np.amin(x);
    float min = np.amin(x_min);

    // axis=null causes exception!
    NDArray x_max = np.amax(x);
    float max = np.amax(x_max);

    float diff = max - min;
    if (diff == 0) { diff = 1e-7f; }

    NDArray r = np.zeros(x.shape, TF_DataType.TF_FLOAT);

    NDArray x_min2 = np.full(x[0].shape, min * -1.0f);
    NDArray x_minmax = np.full(x[0].shape, 1.0f / diff);

    r = np.add(x, x_min2);
    r = np.multiply(r, x_minmax);

    return r;
}
  • np.min(),np.max()はないので、amin(),amax()を用いています。
  • 行列どうしの演算が単一値を返す場合があるので、行列をnp.full()で復元しています。
  • 浮動小数点数の型が標準でdoubleになる場合があるので、明示的にfloat(TF_DataType.TF_FLOAT)を指定してます。

# 四則演算をmethod呼び出しで記述しているのは、試行錯誤の跡です。

InputLayer.cs
public static NDArray Z_Score(NDArray x)
{
    float x_mean = np.mean(x);
    NDArray mean = np.full(x.shape, x_mean * -1.0f);

    // x_i - avg(x)
    NDArray diff = np.add(x, mean);

    NDArray s2 = np.multiply(diff, diff);
    float total = np.sum(s2);
    float avg = total / x.size;
    float sd = (float)Math.Sqrt(avg);

    NDArray rsd = np.full(x[0].shape, (1.0f / sd));            
    NDArray r = np.multiply(diff, rsd);

    return r;
}
  • np.std()がないので、処理を記述しています。

中間層

MiddleLayer.cs
const float h = 1e-4f;

public static NDArray Middle_Back_Func(NDArray x)
{
    return ReLU_Back(x);
}

public static NDArray Middle_Func(NDArray x)
{
    return ReLU(x);
}

Middle_Back_Func()は(誤差逆伝搬法2)で導入されたもの。

MiddleLayer.cs
public static NDArray Middle_Back_wo_Calc(NDArray dz, NDArray x)
{
    NDArray du = Middle_Back_Func(x);
    NDArray r = dz * du;

    return r;
}

public static NDArray Middle_Back(NDArray dz, NDArray x)
{
    NDArray work = x;   // save
    NDArray ha = np.full(x.shape, h);

    x = work + ha;
    ;   // for breakpoint
    float xph = Middle_Func(x);

    x = work - ha;
    float xmh = Middle_Func(x);

    float du = (xph - xmh) / (h * 2.0f);

    x = work;   // restore

    NDArray r = dz * du;

    return r;
}

wo_Calcを付けたものは、(誤差逆伝播法2)で導入されたもの。

  • Pythonだとx = work + hで済むようですが、ha = np.full(..)で明示的に行列を生成してから加算します。
MiddleLayer.cs
 public static NDArray Affine(NDArray z, NDArray W, NDArray b)
 {
     // NDArray r = np.dot(z, W) + b;
     NDArray axes = new NDArray(new int[] { 1, 0 });
     NDArray mp = tf.dot_prod(z, W, axes).numpy() + b;

     return mp;
 }

 public static (NDArray dz, NDArray dW, NDArray db) Affine_Back(NDArray dx, NDArray z, NDArray W, NDArray b)
 {
     NDArray axes = new NDArray(new int[] { 1, 0 });
     NDArray zT = tf.transpose(z).numpy();
     NDArray WT = tf.transpose(W).numpy();

     NDArray dz = tf.dot_prod(dx, WT, axes).numpy();
     NDArray dW = tf.dot_prod(zT, dx, axes).numpy();

     int size = z.ndim == 2 ? (int)z.shape[0] : 1;
     NDArray onesT = np.ones(size, TF_DataType.TF_FLOAT).reshape((1,size));
     NDArray db = tf.dot_prod(onesT, dx, axes).numpy();

     return (dz, dW, db);
 }

アフィン変換の部分。

  • Pythonの場合と異なり、np.dot()は、2次元以上の場合、内部的にflattenして演算するようなので、tf.dot_prod(..)を代わりに用います。
  • dot_prodの3つめの引数axesは、2つの引数のうち、前者を2次元(1)、後者を1次元(0)として扱うことを指示します。
MiddleLayer.cs
public static NDArray ReLU_Back(NDArray x)
{
    NDArray ones = np.full<float>(x.shape, 1.0f);
    NDArray zeros = np.full<float>(x.shape, 0.0f);
    NDArray r = tf.where(x > 0.0f, ones, zeros).numpy();

    return r;
}

public static NDArray ReLU(NDArray x)
{
    NDArray zero = np.zeros(x.shape, TF_DataType.TF_FLOAT);
    NDArray r = np.maximum(zero, x);

    return r;
}
  • ReLU_Backは、Pythonだとnp.where(x > 0, 1, 0)で済むようですが、明示的に行列を生成します。また、np.where()がないので代わりにtf.where(..)を用いています。

出力層

OutputLayer.cs
public static NDArray Output_Error_Back_Func(NDArray y, NDArray x, NDArray t)
{
    return SoftMax_Cross_Entropy_Error_Back(y, x, t);
}

public static NDArray Output_Func(NDArray x)
{
    return SoftMax(x);
}

(誤差逆伝播法)での実装です。

OutputLayer.cs
public static NDArray Output_Error_Back_wo_Calc(NDArray y, NDArray x, NDArray t)
{
    return Output_Error_Back_Func(y, x, t);
}

public static NDArray Output_Error_Back(NDArray x, NDArray t)
{
    float h = 1e-4f;

    NDArray dx = np.zeros(x.shape, TF_DataType.TF_FLOAT);

    (int, int)[] tuples = Common.Ndenumerate(x);

    foreach (var tuple in tuples)
    {
        float work = x[tuple.Item1, tuple.Item2]; // save

        x[tuple.Item1, tuple.Item2] = work + h;
        NDArray y = Output_Func(x);
        float xph = Training.Error_Func(y, t);

        x[tuple.Item1, tuple.Item2] = work - h;
        y = Output_Func(x);
        float xmh = Training.Error_Func(y, t);

        dx[tuple.Item1, tuple.Item2] = (xph - xmh) / (h * 2f);

        // x[tuple.Item1, tuple.Item2] = work;     // restore
    }

    return dx;
}

(誤差逆伝播法2)での実装です。

  • np.denumerate()の代わりに、行と列の組合せを保持するtupleを返すNdenumerate()を作成して用いています。
  • workの値をもどす処理は、ここでは意味はないですね。
OutputLayer.cs
public static NDArray Identity(NDArray x)
{
    return x;
}

public static NDArray SoftMax_Cross_Entropy_Error_Back(NDArray y, NDArray x, NDArray t)
{
    float size = y.ndim == 2.0f ? y.shape[0] : 1.0f;

    NDArray r = (y - t) / size;

    return r;
}

public static NDArray SoftMax(NDArray x)
{
    // instead of x.T
    Tensor xT = tf.transpose(x);

    Tensor exp_x = tf.exp(xT);
    Tensor sum_exp_x = tf.sum(exp_x, 0);
    Tensor r = exp_x / sum_exp_x;

    Tensor rT = tf.transpose(r);

    return rT.numpy();
}

public static NDArray He_Normal(int d_1, int d)
{
    float std = np.sqrt(2.0f / d_1);
    // float std2 = (float)Math.Sqrt(2.0f / d_1);
    NDArray r = np.random.normal(0, std, (d_1, d));
    r = r.astype(TF_DataType.TF_FLOAT);

    return r;
}
  • Pythonではx = x.Tと行列を転置できますが、代わりにtf.transpose()を用いています。
  • He_Normalでは、値を返すときに明示的にTF_DataType.TF_FLOATを指示しています。np.random.normal()の結果をそのまま返すと、doubleの扱いとなり、後続の処理で型不整合のエラーになります。

トレーニング

Training.cs
const float h = 1e-4f;
const float eta = 0.01f;    // learning rate

private NDArray _W1;
private NDArray _W2;
private NDArray _W3;
private NDArray _b1;
private NDArray _b2;
private NDArray _b3;

public NDArray W1 { get { return _W1; } }
public NDArray W2 { get { return _W2; } }
public NDArray W3 { get { return _W3; } }
public NDArray b1 { get { return _b1; } }
public NDArray b2 { get { return _b2; } }
public NDArray b3 { get { return _b3; } }

// Constructor
public Training(NDArray w1, NDArray w2, NDArray w3, NDArray bias1, NDArray bias2, NDArray bias3)
{
    _W1 = w1;
    _W2 = w2;
    _W3 = w3;

    _b1 = bias1;
    _b2 = bias2;
    _b3 = bias3;
}

public void UpdateValues(NDArray dW1, NDArray dW2, NDArray dW3, NDArray db1, NDArray db2, NDArray db3)
{
    _W1 = _W1 - eta * dW1;
    _b1 = _b1 - eta * db1;
    _W2 = _W2 - eta * dW2;
    _b2 = _b2 - eta * db2;
    _W3 = _W3 - eta * dW3;
    _b3 = _b3 - eta * db3;

    float W1min = np.amin(_W1);
    float W1avg = np.mean(_W1);
    float W1max = np.amax(_W1);
    Console.WriteLine(String.Format("  W1 min:{0:F6}, avg:{1:F6}, max:{2:F6}",W1min,W1avg,W1max));

    float W2min = np.amin(_W2);
    float W2avg = np.mean(_W2);
    float W2max = np.amax(_W2);
    Console.WriteLine(String.Format("  W2 min:{0:F6}, avg:{1:F6}, max:{2:F6}", W2min, W2avg, W2max));

    float W3min = np.amin(_W3);
    float W3avg = np.mean(_W3);
    float W3max = np.amax(_W3);
    Console.WriteLine(String.Format("  W3 min:{0:F6}, avg:{1:F6}, max:{2:F6}", W3min, W3avg, W3max));
}

重み付け変数とバイアス変数を定義しています。学習の都度更新される値をクラス変数として保持しています。
値を更新する処理では、動作確認用にW1,W2,W3の値の変化を表示しています。

Training.cs
public static float Error_Func(NDArray y, NDArray t)
{
    return Cross_Entropy_Error(y, t);
    // return Mean_Squared_Error(y, t);
}

public static float Mean_Squared_Error(NDArray y, NDArray t)
{
    float size = y.ndim == 2 ? y.shape[0] : 1;

    NDArray s2 = np.power((y - t), 2.0f);
    float e = np.sum(s2) * 0.5f / size;

    return e;
}

public static float Cross_Entropy_Error(NDArray y, NDArray t)
{
    float size = y.ndim == 2 ? y.shape[0] : 1;

    NDArray log = np.log(y);
    NDArray mul = t * log;
    float e = np.sum(mul) * -1.0f / size;

    return e;
}

誤差を計算する処理を、どちらか選択します。

Training.cs
public static float Accuracy_Rate(NDArray y, NDArray t)
{
    NDArray max_y = np.argmax(y, axis: 1);
    NDArray max_t = np.argmax(t, axis: 1);

    // double r = np.sum(max_y == max_t) / y.shape[0];
    float s = 0;
    for (int i = 0;i < (int)max_y.size; i++)
    {
        s += max_y[i] == max_t[i] ? 1 : 0;
    }
    float r = s / y.shape[0];

    return r;
}
  • Pythonだとnp.sum(max_y == max_t)と書けるところ、機能しなかったので、for文で回しています。
Training.cs
// z0b; z0 batch unit
// t0b; t0 batch unit
public void PropagationAndCalcGradient_wo_Calc(NDArray z0b, NDArray t0b)
{
    // middle layer1
    NDArray u1 = MiddleLayer.Affine(z0b, _W1, _b1);
    NDArray z1 = MiddleLayer.Middle_Func(u1);

    // middle layer2
    NDArray u2 = MiddleLayer.Affine(z1, _W2, _b2);
    NDArray z2 = MiddleLayer.Middle_Func(u2);

    // output layer
    NDArray u3 = MiddleLayer.Affine(z2, _W3, _b3);
    NDArray y = OutputLayer.Output_Func(u3);

    // calc gradients
    NDArray du1;
    NDArray du2;
    NDArray du3;
    NDArray dz0;
    NDArray dz1;
    NDArray dz2;
    NDArray dW1;
    NDArray dW2;
    NDArray dW3;
    NDArray db1;
    NDArray db2;
    NDArray db3;
    du3 = OutputLayer.Output_Error_Back_wo_Calc(y, u3, t0b);
    (dz2, dW3, db3) = MiddleLayer.Affine_Back(du3, z2, _W3, _b3);
    du2 = MiddleLayer.Middle_Back_wo_Calc(dz2, u2);
    (dz1, dW2, db2) = MiddleLayer.Affine_Back(du2, z1, _W2, _b2);
    du1 = MiddleLayer.Middle_Back_wo_Calc(dz1, u1);
    (dz0, dW1, db1) = MiddleLayer.Affine_Back(du1, z0b, _W1, _b1);

    UpdateValues(dW1, dW2, dW3, db1, db2, db3);
}

変数の受け渡しを減らすため、もとのpropagationと勾配を計算する処理をまとめています。wo_Calcの付いたmethodを付いていないものに変えると(誤差逆伝播法)の処理になります。

Training.cs
public NDArray Propagation3(NDArray x)
{
    // middle layer1
    NDArray u1 = MiddleLayer.Affine(x, _W1, _b1);
    NDArray z1 = MiddleLayer.Middle_Func(u1);

    // middle layer2
    NDArray u2 = MiddleLayer.Affine(z1, _W2, _b2);
    NDArray z2 = MiddleLayer.Middle_Func(u2);

    // output layer
    NDArray u3 = MiddleLayer.Affine(z2, _W3, _b3);
    NDArray y = OutputLayer.Output_Func(u3);

    return y;
}

出力データを計算をする部分です。

MNISTデータの読み込み

学習に用いるMNISTデータですが、オリジナルの配布元は配布を停止したようなので、以下の複写先から入手しました。

MNISTデータを解凍し、NDArrayに変換します。

MNISTManager.cs
public static (NDArray, NDArray, NDArray, NDArray) Load_MNIST(string mnist_path)
{
    return 
        (
        Load_Image(mnist_path + "train-images-idx3-ubyte.gz"),
        Load_Label(mnist_path + "train-labels-idx1-ubyte.gz"),
        Load_Image(mnist_path + "t10k-images-idx3-ubyte.gz"),
        Load_Label(mnist_path + "t10k-labels-idx1-ubyte.gz")
        );
}

学習用のイメージデータとラベル、検査用のイメージデータトラベル、計4ファイルです。

MNISTManager.cs
 public static NDArray Load_Image(string image_path)
 {
     using Stream fs = File.OpenRead(image_path);
     using Stream zs = new GZipStream(fs, CompressionMode.Decompress);

     byte[] buf = new byte[16];
     zs.Read(buf,0,16);
     long size = BinaryPrimitives.ReadInt32BigEndian(buf[4..8]);
     long rows = BinaryPrimitives.ReadInt32BigEndian(buf[8..12]);
     long cols = BinaryPrimitives.ReadInt32BigEndian(buf[12..16]);

     int cnt = (int)size * (int)rows * (int)cols;

     int nread = 0;
     int offset = 0;
     int len = 1024 * 1024;  // 1M

     byte[] readbuf = new byte[len];
     byte[] bufdata = new byte[cnt + len];

     while (true)
     {
         nread = zs.Read(readbuf,0,len);

         // nread can be less than len
         // maybe, 0s in the tail are omitted
         if (nread == 0) { break; }
         if (offset >= cnt) { break; }   // ignore residuals

         // sometimes nread < len ...
         for (var i = 0; i < nread;i++)
         {
             bufdata[offset + i] = readbuf[i]; 
         }
         // readbuf.CopyTo(bufdata, offset); // this copys unread data...

         offset += nread;
     }

     NDArray data = np.array(bufdata[0..cnt]).reshape((size, rows * cols));
     data = data.astype(TF_DataType.TF_FLOAT);

     return data;
 }

イメージデータの読み取り処理です。
最初にヘッダを読み取り、格納する画像数、画像のピクセルの行数と列数を取り出します。
ついで、画像数を満たすまで、データを読み取ります。
最後、reshapeでデータの形状を与え、astypeでfloat型を指定します。

# こなれた処理ではありませんが、一度しか実行しない部分なのでよしとします。

MNISTManager.cs
public static NDArray Load_Label(string label_path)
{
    using Stream fs = File.OpenRead(label_path);
    using Stream zs = new GZipStream(fs, CompressionMode.Decompress);

    byte[] buf = new byte[8];
    zs.Read(buf,0,8);
    long size = BinaryPrimitives.ReadInt32BigEndian(buf[4..8]);

    int cnt = (int)size;

    int nread = 0;
    int offset = 0;
    int len = 1024 * 1024;  // 1M

    byte[] readbuf = new byte[len];
    byte[] bufdata = new byte[size + len];

    while (true)
    {
        nread = zs.Read(readbuf, 0, len);

        if (nread == 0) { break; }
        if (offset >= cnt) { break; }

        for (var i = 0;i < nread; i++)
        {
            bufdata[offset + i] = readbuf[i];
        }

        offset += nread;
    }

    NDArray data = np.array(bufdata[0..cnt]);

    NDArray label = np.zeros(((int)data.size, 10), TF_DataType.TF_FLOAT);
    for (int i = 0; i < (int)data.size; i++)
    {
        label[i, data[i]] = (float)1;
    }

    return label;
}

同様にラベルデータの読み取り処理です。

道具類

.NET版numpyに未実装の機能などを作り付けます。

Common.cs
public static (int, int)[] Ndenumerate(NDArray x)
{
    int sz1 = (int)x.shape[0];
    int sz2 = (int)x.shape[1];

    (int, int)[] tuples = new (int, int)[sz1 * sz2];

    int idx = 0;
    for (int i = 0; i < sz1; i++)
    {
        for (int j = 0; j < sz2; j++)
        {
            tuples[idx++] = (i, j);
        }
    }

    return tuples;
}

np.ndenumerateは実装されていないので、行列の行と列の一覧をtupleで返す処理を実装します。

Common.cs
public static (NDArray rdata, NDArray rlabel) ShuffleData(NDArray data, NDArray label)
{
    long szData = data.shape[0];
    long szLabel = label.shape[0];

    if (szData != szLabel) { throw new Exception("Data and Label has different size."); }

    NDArray idx = np.zeros(new Shape(szData), TF_DataType.TF_INT32);
    for (int i = 0; i < szData; i++) { idx[i] = i; }
    np.random.shuffle(idx);

    NDArray rdata = np.zeros(data.shape, TF_DataType.TF_FLOAT);
    NDArray rlabel = np.zeros(label.shape, TF_DataType.TF_FLOAT);

    for (int i = 0; i < szData; i++)
    {
        int j = idx[i];
        rdata[i] = data[j];
        rlabel[i] = label[j];
    }

    return (rdata, rlabel);
}

Pythonの実装通りでは、うまく動作しなかったので、乱数列の配列を生成し、それにしたがって並び替える処理を実装します。

TensorFlow.NETに実装されている機能の活用

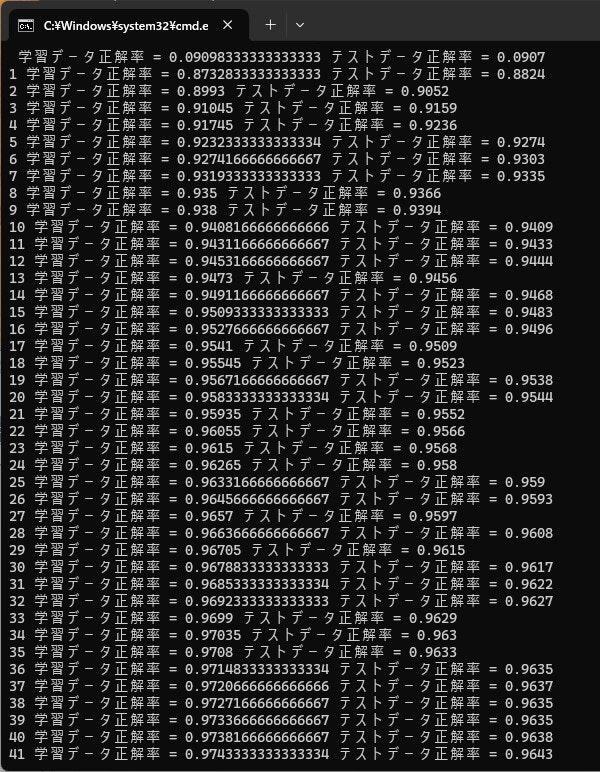
TensorFlow.NETのGitHubのページには、ニューラルネットを用いてMNISTデータを処理するサンプルがあります。

このサンプルを参考に、TensorFlow.NETに実装されている機能を用いて同等の処理を記述してみたので、参考に示します。TensorFlow.NETの活用法としてはこちらが本命です。実際、60000件の学習にかかる時間は数秒と高速でした。

# 実装例では、画面出力で遅くなっています。
# ファイル名は、Programクラスをpartialで定義して別ファイルにしたものです。

Program_tfnative.cs
static void tfnative(NDArray trainData, NDArray trainLabel, NDArray testData, NDArray testLabel)
{
    int batch_size = 100;
    float eta = 0.001f;  // learning rate

    Session session;

    tf.compat.v1.disable_eager_execution();

    // Prepare data
    // Tensorflow.NET has DataSets<MnistDataSet>, but don't use it
    NDArray z0train = InputLayer.Init_Func(trainData);
    NDArray z0test = InputLayer.Init_Func(testData);
    // shuffle
    (NDArray z0, NDArray t) = Common.ShuffleData(z0train, trainLabel);

    #region Graph

    // Build graph
    int d0 = 784;   // input
    int d1 = 50;    // middle layer 1
    int d2 = 100;   // middle layer 2
    int d3 = 10;    // output

    Tensor x, y;
    Tensor loss, accuracy;
    Operation optimizer;

    Graph graph = new Graph().as_default();

    // shape -1; adjust automatically 
    x = tf.placeholder(TF_DataType.TF_FLOAT, shape: (-1, d0), name: "X");
    y = tf.placeholder(TF_DataType.TF_FLOAT, shape: (-1, d3), name: "Y");

    // hidden layers
    var fc1 = fc_layer(x, d1, "FC1");
    var fc2 = fc_layer(fc1, d2, "FC2");
    var output = fc_layer(fc2, d3, "OUT");

    // loss
    var error = tf.nn.softmax_cross_entropy_with_logits(labels: y, logits: output);
    loss = tf.reduce_mean(error, name: "loss");

    // GradientDescentOptimizer does not work well...
    // optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss);
    optimizer = tf.train.AdamOptimizer(learning_rate: eta).minimize(loss);

    var correct_prediction = tf.equal(tf.math.argmax(output, 1), tf.math.argmax(y, 1), name: "correct_pred");
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, TF_DataType.TF_FLOAT), name: "accuracy");

    #endregion Graph

    // Create session
    session = tf.Session();

    // Train
    var init = tf.global_variables_initializer();
    session.run(init);

    float loss_val = 100.0f;
    float accuracy_val = 0.0f;
    float loss_test = 100.0f;
    float accuracy_test = 0.0f;

    for (int i = 0; i < z0.shape[0]; i += batch_size)
    {
        Slice slice = new Slice(String.Format("{0}:{1}", i, i + batch_size));
        NDArray z0b = z0[slice];
        NDArray t0b = t[slice];

        session.run(optimizer, (x, z0b), (y, t0b));

        (loss_val, accuracy_val) = session.run((loss, accuracy), (x, z0b), (y, t0b));
        (loss_test, accuracy_test) = session.run((loss, accuracy), (x, z0test), (y, testLabel));

        Console.WriteLine("No.{0}..{1}", i + 1, i + batch_size);
        Console.WriteLine(String.Format(" accuracy of training data: {0:F6}", accuracy_val));
        // Console.WriteLine(String.Format(" loss     of training data: {0:F6}", loss_val));
        Console.WriteLine(String.Format(" accuracy of test data:     {0:F6}", accuracy_test));
        // Console.WriteLine(String.Format(" loss     of test data:     {0:F6}", loss_test));
        ;   // for break point
    }
}

ニューラルネットの層をGraphで定義し、Sessionを作成した後、runで実行する流れです。
必要な部分のみを記述すればよいのでありがたいのですが、隠れた定義がいろいろあって(tfはどこから来たのか、graphは作りっぱなしじゃないか、とか)、中身を知りたい立場からは、少々、とっつきにくい感じがします。

Program_tfnative.cs
static Tensor fc_layer(Tensor x, int nunits, string name)
{
    int in_dim = (int)x.shape[1];

    float sd = (float)Math.Sqrt(2.0f / nunits);

    // var initializer = tf.initializers.he_normal();   // not implemented
    var initW = tf.truncated_normal_initializer(stddev: sd);
    var initb = tf.constant(0.0f, shape: nunits);

    var W = tf.compat.v1.get_variable("W_" + name, dtype: TF_DataType.TF_FLOAT, shape: (in_dim, nunits), initializer: initW);
    var b = tf.compat.v1.get_variable("b_" + name, dtype: TF_DataType.TF_FLOAT, initializer: initb);

    // dot(z, W) + b
    Tensor layer = tf.matmul(x, W.AsTensor()) + b.AsTensor();

    layer = tf.nn.relu(layer);

    return layer;
}

層の定義部です。ほぼサンプルの通りです。

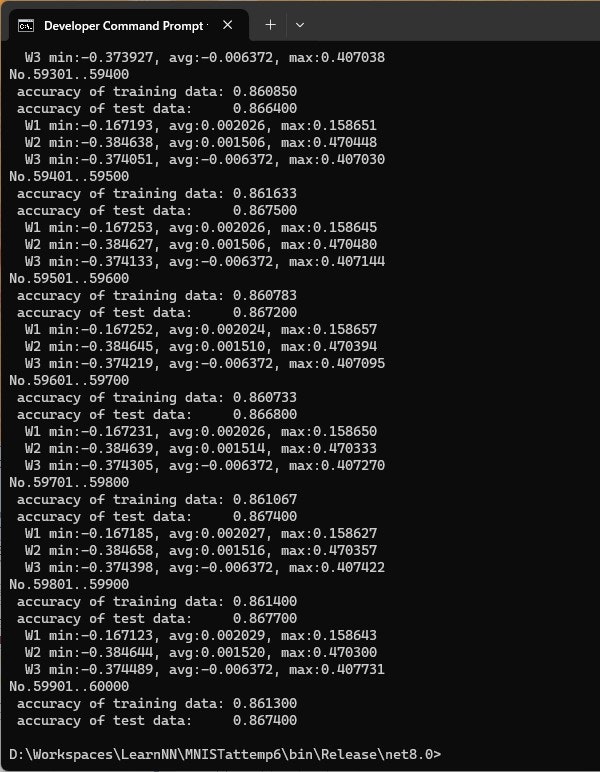
実行結果

実行ログを示します。手許の環境で60000件の学習に12分くらい。87%くらいの精度まで向上しました。

Csharp.jpg

おなじ環境で、元記事のPythonの処理を実行すると、数秒程度です(1epoch分)。精度は87%くらいと変わりません。

python.jpg

TensorFlow.NETでの処理時間が長いのは、CPUの複数のコアを活用できず、ほぼシングル実行になっていることも大きく影響しています。

おわりに

PyThonの実装例を、TensorFlow.NETのnumpyを用いてC#で実装してみました。言語特性の違いから、意識しなくてはいけない点は少なからずありますが、ほぼほぼ元の処理の流れに従って書き下すことができます。
難点は、性能がかなり劣る点です。アルゴリズム等の確認はできるとしても、実用する際には、TensorFlow.NETの本来機能(Tensorを用いた実装)に落とし込む必要があります。
それでも、手慣れたC#で思考できる利点はあると思いますし、学習用としてはおもしろいのではないでしょうか。

# 機械学習や数値計算の試行錯誤用にPyThon(ないしNumPyなどのライブラリ群)が、いかに優れているか再確認したような気がしますけど。

GPUの扱いを含め、C#まわりの環境改善を願いつつ。以上。

0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1