徒競走のタイムと違って、対戦型ゲームの巧さというのは簡単には数値化できません。 しかし、なんとかしてそれを実現させようとして生まれたのがレーティングです。 古典的にはチェスのために生み出された Elo レーティングが存在し、様々な改良アルゴリズムが生み出されてきました。
TrueSkill は Microsoft が開発したレーティングアルゴリズムです。 Microsoft が開発したとあって Xbox Live のゲームで使用されているようです。 このアルゴリズムには既存のレーティングアルゴリズムと比較して以下のような特徴があるそうです。
- 収束が早い。 レーティングに初めて参加するプレイヤーの実力を推定するのに何度も何度も不適当なマッチングで対戦する必要がない。
- 複数人による対戦に対応している。 勝ちか負けかのみならず順位を定めるようなゲームやチーム戦1のゲームにも使用できる。
- ゲームへの参加に重み付けができる。 例えばチームメンバーのひとりが回線トラブルにより途中でゲームから抜けた場合でも適用できる。
Microsoft の息がかかっている。 特許申請と商標登録がなされており、なんとなく手が出しづらい。 あと一部の狂信的 OSS 主義者が憤死する。
ちょろっと論文を読んでみようとは試みたのですが、まず私は英語がてんでダメで、おまけに数学統計学の知識も付け焼き刃なもので、因子グラフとか言われてもさっぱりぽんで無事死亡しました。 私よりはマシという自信がある方は Qiita に投稿されているこちらの記事をお読みいただくと理解を深められると思います。 ぶっちゃけこれと“Computing Your Skill”の和訳記事以外に日本語の資料ないです。 あと Wikipedia もか……?
しかし、私たちには他人の褌があります。 そう、ここに TrueSkill の Python 実装があります。 いくら英語がダメな私でも、Google 先生に頼ればリファレンスくらいは読めるでしょう。 ということで一念発起して TrueSkill で遊んでみて簡単な使い方と遊んだ結果を残すことで数少ない TrueSkill の日本語資料の一つとして労せずうまい汁をすすりたいと思います。 誰かがやめ太郎さん風に書き直して「ワイ『TrueSkill? 転職支援サイトかなんかやろか?』」みたいな感じで投稿するとさらにバズるかもしれません。 次のうまい汁は君だ!
簡単な統計学と TrueSkill の概要
TrueSkill ではプレイヤーのスキルを正規分布に従う確率密度関数によって表現します。 このように序盤から難しそうな単語を出していくことで読者を威圧していくテクニックが荒んだ現代社会で生きのこるには必須と言われています。
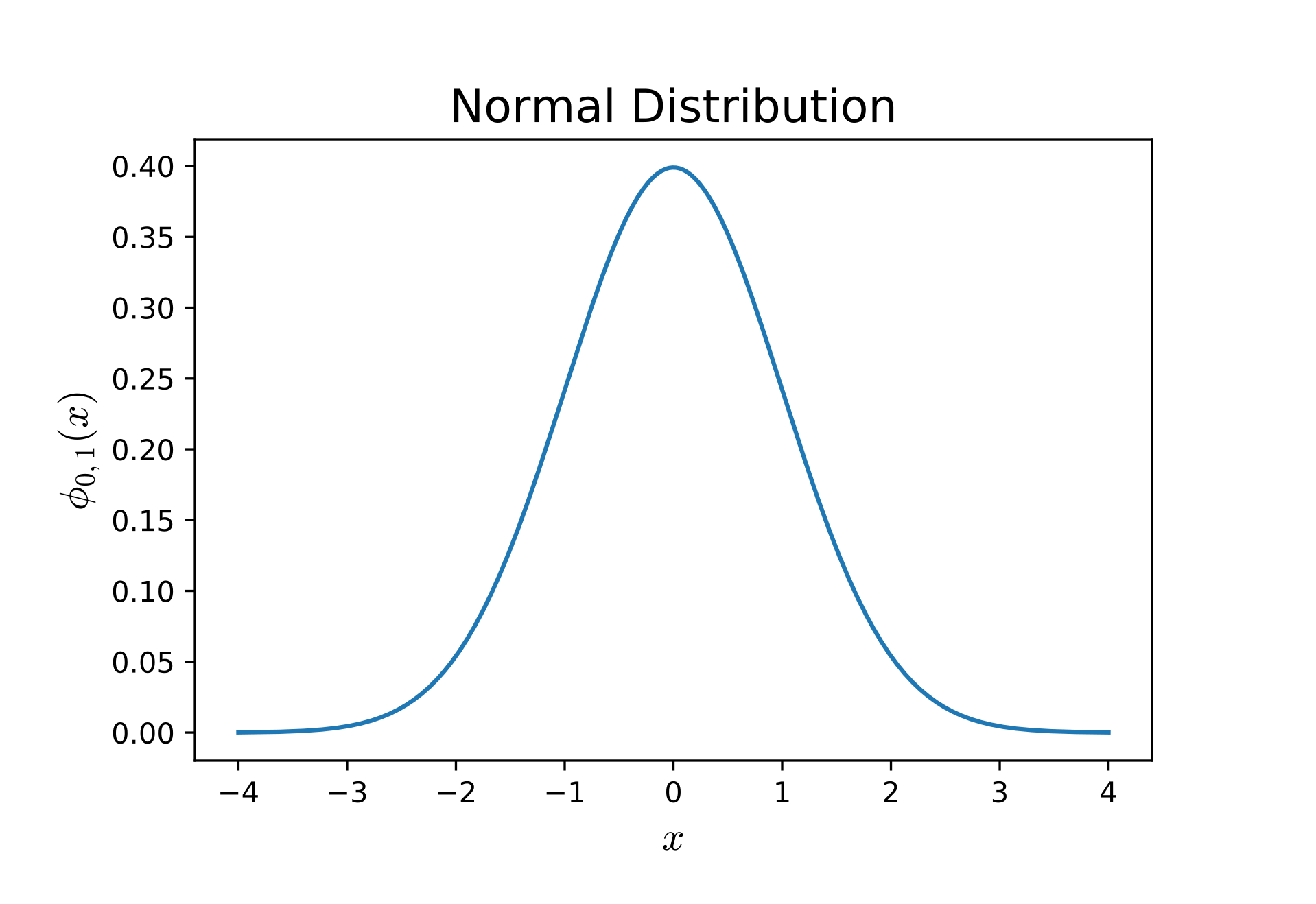
しかし皆さんは私のこの姑息な手法に怯える必要はありません。 まず下の図を見てください。
正規分布とは、まあおおむねこんな形をしたものです。 確率密度関数とは……たとえばそうですね、横軸を「ある値」だとします。 今回の場合はそう、スキルです。 縦軸は……ちょっと違うのですが確率だと思ってください。 正確な話をすると、ちょっとだけ数学的な話になりますが、確率密度関数 $\phi_{\mu, \sigma^2}(x)$ とは2、「ある値」が $x_1$ から $x_2$ の間(ここで $x_1 < x_2$ とします)に収まる確率 $p_{12}$ が $\phi_{\mu, \sigma^2}(x)$ を $x_1$ から $x_2$ まで積分した値、すなわち $p_{12} = \int_{x_1}^{x_2}\phi_{\mu, \sigma^2}(x)$ になるように定めた関数です。 まあ要するに山の頂点周辺の可能性が高いよ関数、と思ってくれればいいです。
ここで私たちが気にしなければいけないことはふたつです。 すなわち、
- 頂点はどこか?
- どれくらい幅があるのか?
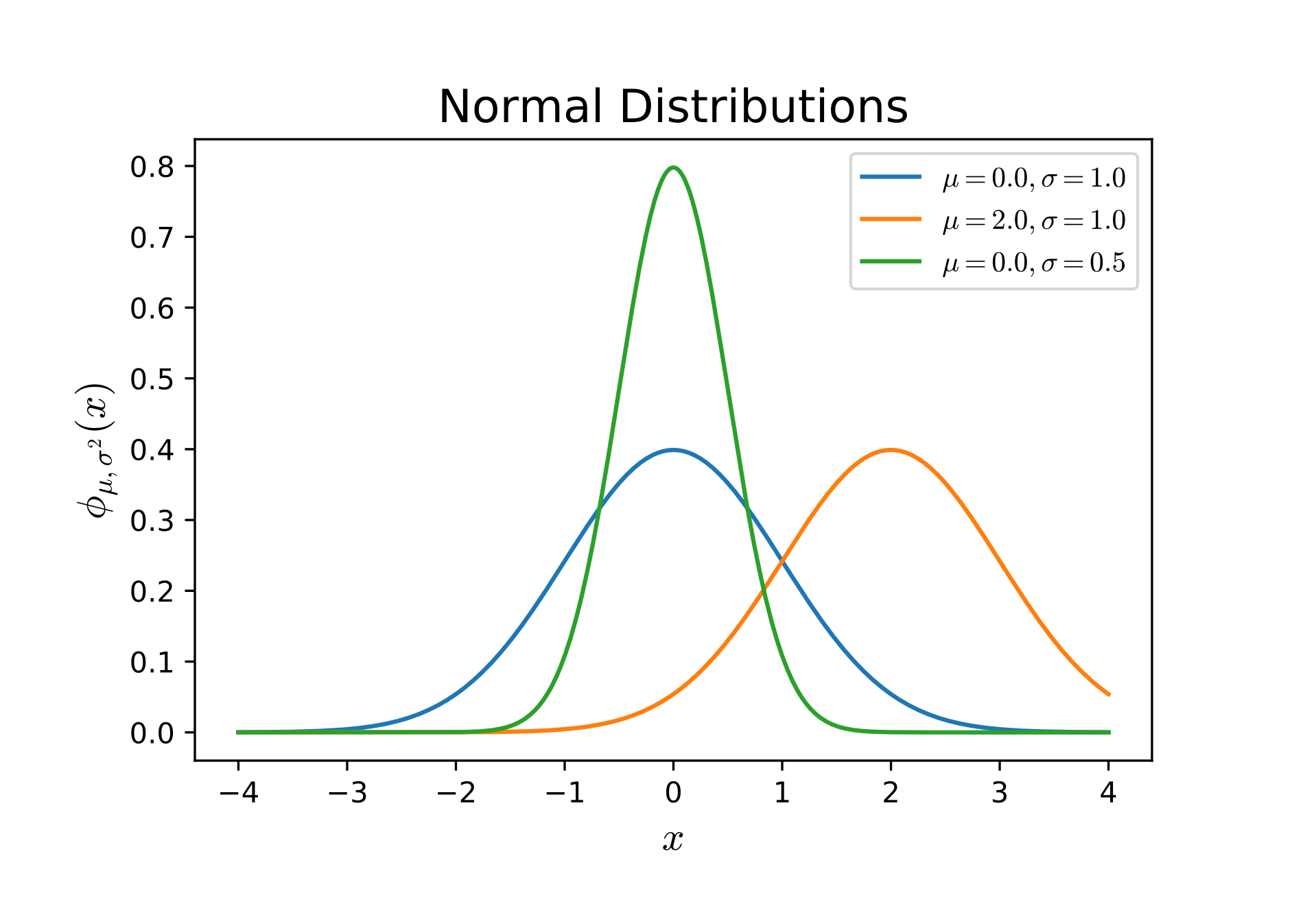
頂点が右にあるほうがよりよいスキルを持っている可能性が高いですし(青に対する橙)、横軸に対する頂点が同じでも幅が狭いほど精密な予測になっているといえます(青に対する緑)。 ちなみに定義上、幅が狭くなれば頂点は高くなります。
前者を教えてくれるのが期待値あるいは平均と呼ばれる数値で、ギリシア文字の $\mu$ やラテン文字の $m$ で表されます。 正規分布における期待値はそのまま山の頂点の横軸成分になります。 マイナス無限からプラス無限まで重み付き積分をしたときの平均、ということなんだと……思います……。(統計クソザコマン)
後者を教えてくれるのが標準偏差と呼ばれる数値で、ギリシア文字の $\sigma$ やラテン文字の $s$ で表されます。 ちなみに、「ある値」が $\mu \pm \sigma$ の範囲に収まっている確率は、定義から計算すると約 68% になります。 これが $\mu \pm 3\sigma$ になるとほぼ確実3となり、この $3\sigma$ という指標は実用上よく利用されます。 外れ値の検出とかね。
TrueSkill ではこの 2 種類の値によってプレイヤーのスキルを推測します。
プレイヤーが勝てば $\mu$ は上昇し、負ければ $\mu$ は減少します。 いずれにせよ $\sigma$ は減少し4、推測がより正確になったことを示します。 プレイヤーに提示される数値は $\mu - 3\sigma$ という、期待値をより「控えめ」に見積もった値で、これは Python 実装のリファレンスでは“rating exposure”と表現されています。 どう訳すのが適切かはよくわかりませんが、とりあえず本稿では「顕在化レート / 顕在化レーティング」としておきます。
はじめて TrueSkill のレーティングシステムに参加したプレイヤーの値は $\mu = 25, \sigma = \frac{25}{3}$ で与えられます。 顕在化レーティングはちょうど 0 となります。
利用してみる
堅苦しい理論はここまでにして、実際に TrueSkill を利用してみましょう。
当然の権利のように PyPI に登録されていますので、pipを使用して簡単にインストールできます。
$ pip install trueskill
インポートするにはこうです。
import trueskill
環境
TrueSkill によるレーティング計算を行うには、環境を用意します。 環境といってもなにかをインストールするとかそういう意味ではなく、いわば**「利用する定数を設定する」**くらいの意味合いで考えて下さい。
新しい環境を生成するにはtrueskill.TrueSkillコンストラクタを呼び出します。
mu = 25.
sigma = mu / 3.
beta = sigma / 2.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
env
trueskill.TrueSkill(mu=25.000, sigma=8.333, beta=4.167, tau=0.083, draw_probability=10.0%)
パラメータmuとsigmaは、より実態に即した表記をすると $\mu_0$ および $\sigma_0$ で、$\mu$ および $\sigma$ の初期値を示します。 デフォルト値は25.および8.333333333333334です。
パラメータbetaは 76% の勝率を保証するスキル差です。 チェスや将棋や囲碁のような、運の要素が絡まないゲームにおいてはこの値は小さく、麻雀のような多少の実力差を運でカバーできるゲームではこの値は大きくするのが理想的です。 デフォルト値は4.166666666666667です。
パラメータtauはスキルの再計算を行うときに問答無用で $\sigma$ に与えられます。 これは不確かさを示し、ゲームのダイナミクスを表現するとか、$\sigma$ が 0 になって更新が停滞するのを防ぐとかの意味があるようです。 デフォルト値は0.08333333333333334です。
パラメータdraw_probabilityは、名前の通り 2 チーム(あるいはふたり)が引き分けになる確率です。 float値で入力することもできますが、floatを返却する関数を与えることもできるそうです(未確認)。 デフォルト値は0.1です。
パラメータbackendは計算に使用するバックエンドを指定します。 利用可能なバックエンドは'scipy'と'mpmath'です。 Noneでは TrueSkill モジュール自前のものを使用します。 デフォルト値はNoneです。
以降は主にこの環境に対してメソッドを呼び出すことによって TrueSkill を利用していきます。 例えば、以下のような具合です。
alice = env.create_rating()
bob = env.create_rating()
(alice,),(bob,), = env.rate(((alice,), (bob,),), ranks=[0, 1,])
print(f'Alice\'s rating exposure: {env.expose(alice):.3f}')
print(f' Bob\'s rating exposure: {env.expose(bob):.3f}')
Alice's rating exposure: 7.881
Bob's rating exposure: -0.910
ユーザが生成する環境のほかにも、あらかじめ設定されたグローバル環境を利用することもできます。 グローバル環境はtrueskill.global_env関数で呼び出すことができます。 グローバル環境の初期値は前述のデフォルト値になっています。
trueskill.global_env()
trueskill.TrueSkill(mu=25.000, sigma=8.333, beta=4.167, tau=0.083, draw_probability=10.0%)
グローバル環境を取得してメソッドコールをすることもできますが、多くのメソッドには代替(proxy)関数が存在します。
| メソッドコール | 代替関数 |
|---|---|
| trueskill.global_env().rate | trueskill.rate |
| trueskill.global_env().quality | trueskill.quality |
| trueskill.global_env().expose | trueskill.expose |
生成した環境をグローバル環境に登録するにはmake_as_globalメソッドを使用します。
env = trueskill.TrueSkill(mu=50.)
env.make_as_global()
trueskill.global_env()
trueskill.TrueSkill(mu=50.000, sigma=8.333, beta=4.167, tau=0.083, draw_probability=10.0%)
trueskill.setup関数を使用すると直接グローバル環境の設定を変更することができます。
trueskill.setup(mu=10., sigma=10./3., beta=10./6., tau=10./300.)
trueskill.global_env()
trueskill.TrueSkill(mu=10.000, sigma=3.333, beta=1.667, tau=0.033, draw_probability=10.0%)
レーティングとチーム
環境に対しcreate_ratingメソッドを呼び出すことで各プレイヤーのレーティングを示すRatingオブジェクトを生成できます。 create_ratingにmuパラメータおよびsigmaパラメータを与えることで初期値以外のレーティングを生成することもできます。 レーティングはmuプロパティおよびsigmaプロパティをもちます。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating(mu=30, sigma=4)
(r1.mu,r1.sigma,),(r2.mu,r2.sigma,),
((25.0, 8.333333333333334), (30.0, 4.0))
Ratingオブジェクトのコンストラクタを直接呼び出した場合、グローバル環境が利用されます。
r1 = trueskill.Rating()
trueskill.setup(mu=10., sigma=10./3., beta=10./6., tau=10./300.)
r2 = trueskill.Rating()
r1,r2,
(trueskill.Rating(mu=25.000, sigma=8.333),
trueskill.Rating(mu=10.000, sigma=3.333))
環境に対しexposeメソッドを呼び出し、パラメータにレーティングオブジェクトを与えることでそのレーティングオブジェクトの顕在化レーティングを得ることができます。 Wikipedia 情報によると 0 - 50 のスケールが使用されているそうですが、このメソッドの返却値はクリッピングなどは行わないので注意が必要です。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating(mu=30, sigma=4)
r3 = env.create_rating(mu=10, sigma=5)
env.expose(r1),env.expose(r2),env.expose(r3),
(0.0, 18.0, -5.0)
ゲームに参加する 1 単位のことをチームといいます。 チームはレーティングオブジェクトのリストまたはタプルか、値にレーティングオブジェクトをもつ辞書です。 たとえ 1 対 1 のゲームであってもチームを形成します。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
t1 = (r1,r2,)
t1
(trueskill.Rating(mu=25.000, sigma=8.333),
trueskill.Rating(mu=25.000, sigma=8.333))
レーティングの更新
rateメソッドを呼び出すことでレーティングの更新を行います。 第一パラメータにはチームのリストかタプルを、ranksパラメータには順位(プログラムの世界なので 0 始まりです)のリストかタプルを与えます。 更新されたチームのリストが返却されます。 前述したとおりチームには複数の書式がありますが、rateメソッドに渡すチームの書式は統一されている必要があります。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r3 = env.create_rating()
r4 = env.create_rating()
t1 = {'player1': r1, 'player2': r2,}
t2 = {'player3': r3, 'player4': r4,}
t1,t2, = env.rate((t1,t2,), ranks=(1,0,))
t1,t2,
({'player1': trueskill.Rating(mu=21.892, sigma=7.774),
'player2': trueskill.Rating(mu=21.892, sigma=7.774)},
{'player3': trueskill.Rating(mu=28.108, sigma=7.774),
'player4': trueskill.Rating(mu=28.108, sigma=7.774)})
ranksパラメータを与えなかった場合、記述した通りの順位だったとみなして計算を行います。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r3 = env.create_rating()
r4 = env.create_rating()
t1 = {'player1': r1, 'player2': r2,}
t2 = {'player3': r3, 'player4': r4,}
t1,t2, = env.rate((t1,t2,))
t1,t2,
({'player1': trueskill.Rating(mu=28.108, sigma=7.774),
'player2': trueskill.Rating(mu=28.108, sigma=7.774)},
{'player3': trueskill.Rating(mu=21.892, sigma=7.774),
'player4': trueskill.Rating(mu=21.892, sigma=7.774)})
前述したとおり、たとえ 1 対 1 のゲームであってもチームを形成します。 rateメソッドにレーティングオブジェクトを直接渡すことはできないので注意してください。
# 間違い
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r1,r2 = env.rate((r1,r2,))
r1,r2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-11-08f690b7e5cd> in <module>
6 r2 = env.create_rating()
7
----> 8 r1,r2 = env.rate((r1,r2,))
9
10 r1,r2
f:\trueskill_test\venv\lib\site-packages\trueskill\__init__.py in rate(self, rating_groups, ranks, weights, min_delta)
475
476 """
--> 477 rating_groups, keys = self.validate_rating_groups(rating_groups)
478 weights = self.validate_weights(weights, rating_groups, keys)
479 group_size = len(rating_groups)
f:\trueskill_test\venv\lib\site-packages\trueskill\__init__.py in validate_rating_groups(self, rating_groups)
272 raise TypeError('All groups should be same type')
273 elif group_types.pop() is Rating:
--> 274 raise TypeError('Rating cannot be a rating group')
275 # normalize rating_groups
276 if isinstance(rating_groups[0], dict):
TypeError: Rating cannot be a rating group
# 正解
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
((r1,),(r2,),) = env.rate(((r1,),(r2,),))
r1,r2,
(trueskill.Rating(mu=29.396, sigma=7.171),
trueskill.Rating(mu=20.604, sigma=7.171))
rateメソッドのweightsパラメータに 2 次元のリストかタプルを与えることで、ゲームの参加率を加味したレーティングの更新を行います。 チームと異なり、辞書による書式は使用できません。 チームを辞書で記述した場合順序が保証されませんので後述する書式によって参加率を記述するのが基本になります。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r3 = env.create_rating()
r4 = env.create_rating()
t1 = (r1,r2,)
t2 = (r3,r4,)
teams = (t1,t2,)
w1 = (1,1,)
w2 = (0.5,1,) # プレイヤー3はゲームの半分が経過した時点で回線落ちした、など
weights = (w1,w2,)
t1,t2, = env.rate(teams, weights=weights)
t1,t2,
((trueskill.Rating(mu=26.738, sigma=7.844),
trueskill.Rating(mu=26.738, sigma=7.844)),
(trueskill.Rating(mu=24.131, sigma=8.214),
trueskill.Rating(mu=23.262, sigma=7.844)))
そもそもチーム 2 が不利な状況で負けたためか先程までの例にくらべレーティングの上昇/下降幅が小さく、また参加時間が少なかったプレイヤー 3 の $\sigma$ がほかの 3 人にくらべてあまり減っていないのがわかります。
現実問題としては、ほぼ全員の参加率が 1 で一部のプレイヤーのみが少ない、という傾向になると予想できます。 こういった場合、リストおよびタプルによる参加率の書式は、参加人数が増えたときに煩雑な記述になる問題があります。 そこで、参加率が 1 に満たないプレイヤーだけを辞書によって記述する方法があります。 キーをチーム順とメンバー順(チームの書式がリストまたはタプルの場合)/チーム順とプレイヤー名のキー(チームの書式が辞書の場合)のタプルとすることでプレイヤーを特定し、値として参加率を記述します。 言葉で説明してもイメージしづらいと思うので、以下のコードで確認してください。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r3 = env.create_rating()
r4 = env.create_rating()
t1 = (r1,r2,)
t2 = (r3,r4,)
teams = (t1,t2,)
weights = {(1,0,): 0.5}
t1,t2, = env.rate(teams, weights=weights)
t1,t2,
((trueskill.Rating(mu=26.738, sigma=7.844),
trueskill.Rating(mu=26.738, sigma=7.844)),
(trueskill.Rating(mu=24.131, sigma=8.214),
trueskill.Rating(mu=23.262, sigma=7.844)))
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
r3 = env.create_rating()
r4 = env.create_rating()
t1 = {'player1': r1, 'player2': r2,}
t2 = {'player3': r3, 'player4': r4,}
teams = (t1,t2,)
weights = {(1,'player3',): 0.5}
t1,t2, = env.rate(teams, weights=weights)
t1,t2,
({'player1': trueskill.Rating(mu=26.738, sigma=7.844),
'player2': trueskill.Rating(mu=26.738, sigma=7.844)},
{'player3': trueskill.Rating(mu=24.131, sigma=8.214),
'player4': trueskill.Rating(mu=23.262, sigma=7.844)})
勝率とマッチング品質
驚くべきことに、この Python 実装には勝率を計算する関数が存在しないらしいです。 以下に示すのはリファレンスにも記載がある Juho Snellman によるスニペットを、環境を指定できるように微加筆したものです。 必要なら利用しましょう。
import itertools
import math
def win_probability(team1, team2, env=None):
env = env if env else trueskill.global_env()
delta_mu = sum(r.mu for r in team1) - sum(r.mu for r in team2)
sum_sigma = sum(r.sigma ** 2 for r in itertools.chain(team1, team2))
size = len(team1) + len(team2)
denom = math.sqrt(size * (env.beta * env.beta) + sum_sigma)
return env.cdf(delta_mu / denom)
env = trueskill.TrueSkill(beta=1)
r1 = env.create_rating(mu=30, sigma=0.1)
r2 = env.create_rating(mu=29, sigma=0.1)
t1 = (r1,)
t2 = (r2,)
wp = win_probability(t1, t2, env=env)
wp
0.7591582948828006
どれだけ公平にマッチングできているかを示す指標がqualityメソッドです。 引き分け確率を使用しているようです。 weightsパラメータを与えることができます。
env = trueskill.TrueSkill()
r1 = env.create_rating(mu=30, sigma=3)
r2 = env.create_rating(mu=29, sigma=3)
t1 = (r1,)
t2 = (r2,)
q = env.quality((t1,t2,))
q
0.8038743995638264
ショートカット
TrueSkill の利点が多人数対戦に使えることではあれど、ほかのルールにくらべ 1 対 1 のゲームが圧倒的に多いこともまた事実です5。 そのため 1 対 1 のゲームで利用できるショートカット関数trueskill.rate_1vs1とtrueskill.quality_1vs1が用意されています。 これらの関数にはレーティングオブジェクトを直接渡すことができます。
env = trueskill.TrueSkill()
r1 = env.create_rating()
r2 = env.create_rating()
# (r1,),(r2,), = env.rate(((r1,),(r2,),))
r1,r2, = trueskill.rate_1vs1(r1, r2, env=env)
print(r1)
print(r2)
print()
# (r1,),(r2,), = env.rate(((r1,),(r2,),), ranks=(0,0,))
r1,r2, = trueskill.rate_1vs1(r1, r2, drawn=True, env=env)
print(r1)
print(r2)
print()
# q = env.quality(((r1,),(r2,),))
q = trueskill.quality_1vs1(r1, r2, env=env)
print(q)
trueskill.Rating(mu=29.396, sigma=7.171)
trueskill.Rating(mu=20.604, sigma=7.171)
trueskill.Rating(mu=26.114, sigma=5.678)
trueskill.Rating(mu=23.886, sigma=5.678)
0.5770440474290585
実にスッキリ書けますね。 文字数は増えてるって? カッコの対応がワケワカメになるほうが面倒だしfrom import記法もあるから多少はね。
シミュレーションによるレーティング
「あーなるほどね完全に理解した」したところで、多人数戦ができること、参加率による重み付けができることはわかりましたが、収束が早いというのはどこまで本当なのでしょうか? これは実際に試してみないことにはわかりません。
というわけで、架空のプレイヤーによるゲーム勝敗をシミュレーションし、既存のアルゴリズムと比較してみましょう。
Elo レーティングの理論を利用したシミュレーションの作成
古典的なレーティングアルゴリズムである Elo レーティングは、極めて単純な式でありながらレーティング差から勝率を導き出せるなど、こういったシミュレーションに最適です。
詳細は省きますが、プレイヤー A のレーティングが $R_A$、プレイヤー B のレーティングが $R_B$ であるとき、プレイヤー A の勝率は以下の式で得ることができます。
$$
W_{AB} = \frac{1}{10^{\frac{R_B - R_A}{400}} + 1}
$$
これを利用してシミュレーションスクリプトを書いていきます。
今回想定する架空のプレイヤーは以下のとおりです。
| プレイヤー | 内部レーティング |
|---|---|
| Emu | 2700 |
| Parado | 2700 |
| Niko | 2500 |
| Taiga | 2000 |
| Hiiro | 2000 |
| Kiriya | 1700 |
| Kuroto | 1700 |
| Poppy | 1500 |
軒並み Elo レーティングの「標準プレイヤー」値である 1500 以上ですが、これはファンへの配慮です。 あくまでも重要なのはレーティングの差なので上位プレイヤーから下位プレイヤーまでがまんべんなく存在していなくても問題ないと思います。 ただ、この結果を Elo レーティングによりレーティングしたとき、彼らの中での標準を 1500 とするため、設定した内部レーティングよりも低い結果が出るものと思われます6。
実際に勝敗のシミュレーションを書いたものがこちらのコードになります。 ランダムに二人ごと対戦させ、これを 500 回繰り返します。 引き分けはありません。 結果は CSV ファイルで出力されます。
結果はこんな感じでした。
| index | Match 1 Winner | Match 1 Loser | Match 2 Winner | Match 2 Loser | Match 3 Winner | Match 3 Loser | Match 4 Winner | Match 4 Loser |
|---|---|---|---|---|---|---|---|---|
| 1 | Emu | Parado | Taiga | Hiiro | Niko | Poppy | Kiriya | Kuroto |
| 2 | Emu | Kuroto | Poppy | Hiiro | Kiriya | Taiga | Niko | Parado |
| 3 | Emu | Niko | Kiriya | Kuroto | Hiiro | Poppy | Parado | Taiga |
| 4 | Parado | Poppy | Emu | Taiga | Niko | Kuroto | Hiiro | Kiriya |
| 5 | Niko | Poppy | Hiiro | Kiriya | Taiga | Kuroto | Parado | Emu |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 496 | Kiriya | Taiga | Niko | Kuroto | Hiiro | Poppy | Emu | Parado |
| 497 | Kiriya | Poppy | Emu | Hiiro | Niko | Kuroto | Parado | Taiga |
| 498 | Parado | Taiga | Niko | Kiriya | Emu | Kuroto | Hiiro | Poppy |
| 499 | Emu | Kuroto | Niko | Taiga | Parado | Kiriya | Hiiro | Poppy |
| 500 | Kuroto | Poppy | Parado | Hiiro | Emu | Niko | Kiriya | Taiga |
「Emu が負けるありえない話し!!」とか言い出す神ファンの存在をのぞけば、問題なさそうな結果です。 実際のデータはこちらになります。
Elo レーティングで実験
今回比較対象として、Elo レーティングによるレーティングを行ってみます。 こちらのコードを実行し、ゲームごとのレーティングの推移を確認してみます。 Elo レーティングで使用されるレーティング変動の激しさを示す値 $K$ は、最初の 20 ゲームでは 32 を、それ以降は 24 を使用します。
結果は以下のようになりました。
| プレイヤー | 最終レート |
|---|---|
| Emu | 2006.988 |
| Parado | 2062.846 |
| Niko | 1821.448 |
| Taiga | 1449.791 |
| Hiiro | 1398.873 |
| Kiriya | 1168.829 |
| Kuroto | 1190.664 |
| Poppy | 900.5602 |
とはいえ、前述したように設定値より低く見積もられていますので、Emu との差で見てみましょう。
| プレイヤー | 差 | 差(真) |
|---|---|---|
| Emu | +0.000 | +0.000 |
| Parado | +55.858 | +0.000 |
| Niko | -185.540 | -200.000 |
| Taiga | -557.197 | -700.000 |
| Hiiro | -608.115 | -700.000 |
| Kiriya | -838.159 | -1,000.000 |
| Kuroto | -816.324 | -1,000.000 |
| Poppy | -1,106.428 | -1,200.000 |
確かにある程度設定値にしたがった値になっているようです。
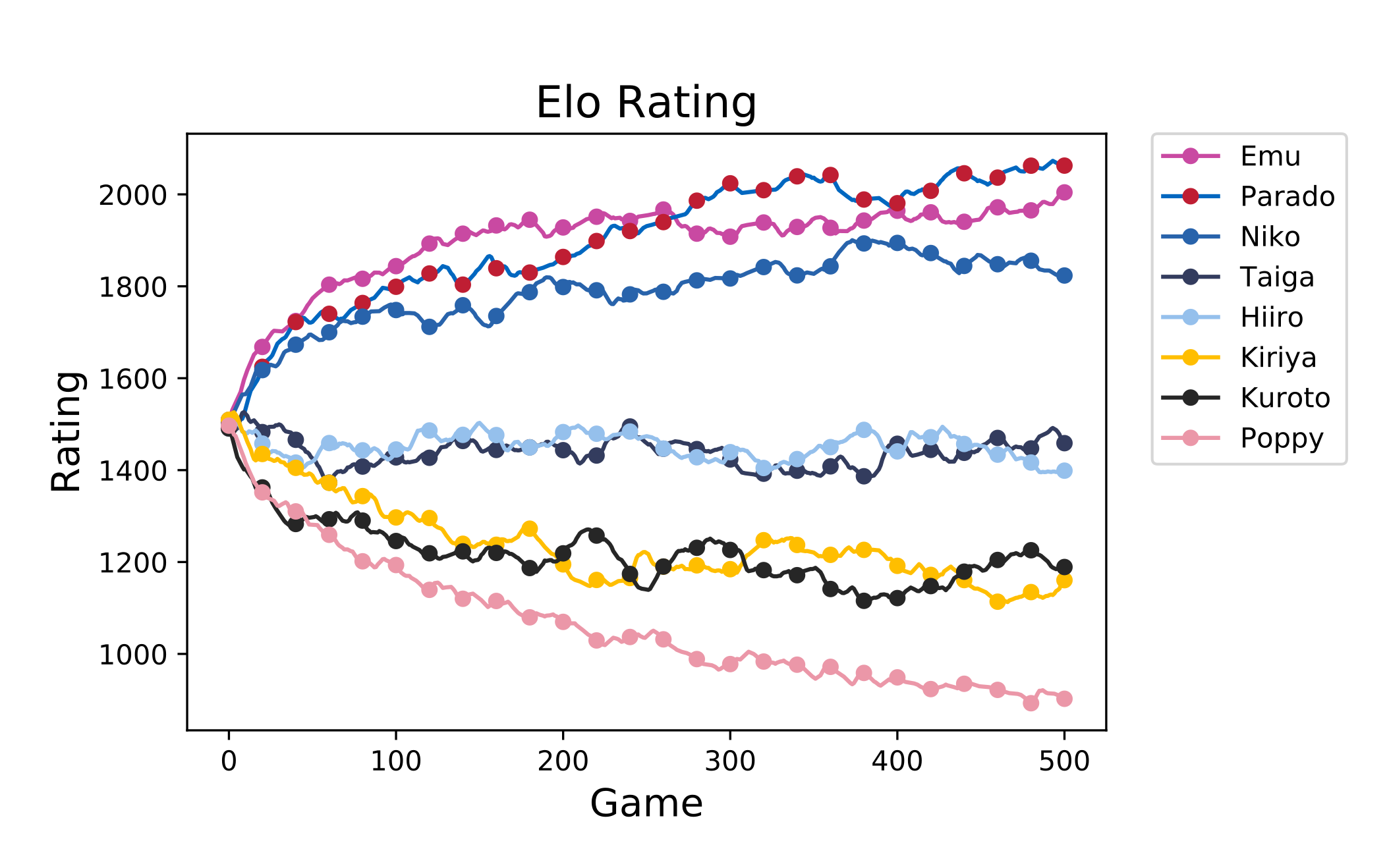
一方で推移は以下のようになっています。 生の値はガクガクして見づらいので 5 点移動平均7で平滑化して示しています。
これを見ると、完全に収束しきっておらず、まだまだ伸びしろがあるように思います。 先程の差も、実際のところ設定値まで広がりきっていません。
TrueSkill で実験
つづいて本命の TrueSkill を試してみましょう。こちらのコードを実行します。
結果は以下のようになりました。
| プレイヤー | 最終顕在化レート | $\mu$ | $\sigma$ |
|---|---|---|---|
| Emu | 32.59123 | 35.70087 | 1.036545 |
| Parado | 34.08617 | 37.20115 | 1.038326 |
| Niko | 29.41995 | 32.34306 | 0.974371 |
| Taiga | 21.1425 | 23.87729 | 0.911596 |
| Hiiro | 20.62174 | 23.38207 | 0.92011 |
| Kiriya | 15.11853 | 17.90101 | 0.927492 |
| Kuroto | 15.4544 | 18.2791 | 0.941565 |
| Poppy | 9.310735 | 12.44336 | 1.044209 |
おおむね順序通り、内部レーティングを同じ値にしたプレイヤーはだいたい同じ値に落ち着いています。 適切にレーティングできていると言っていいでしょう。
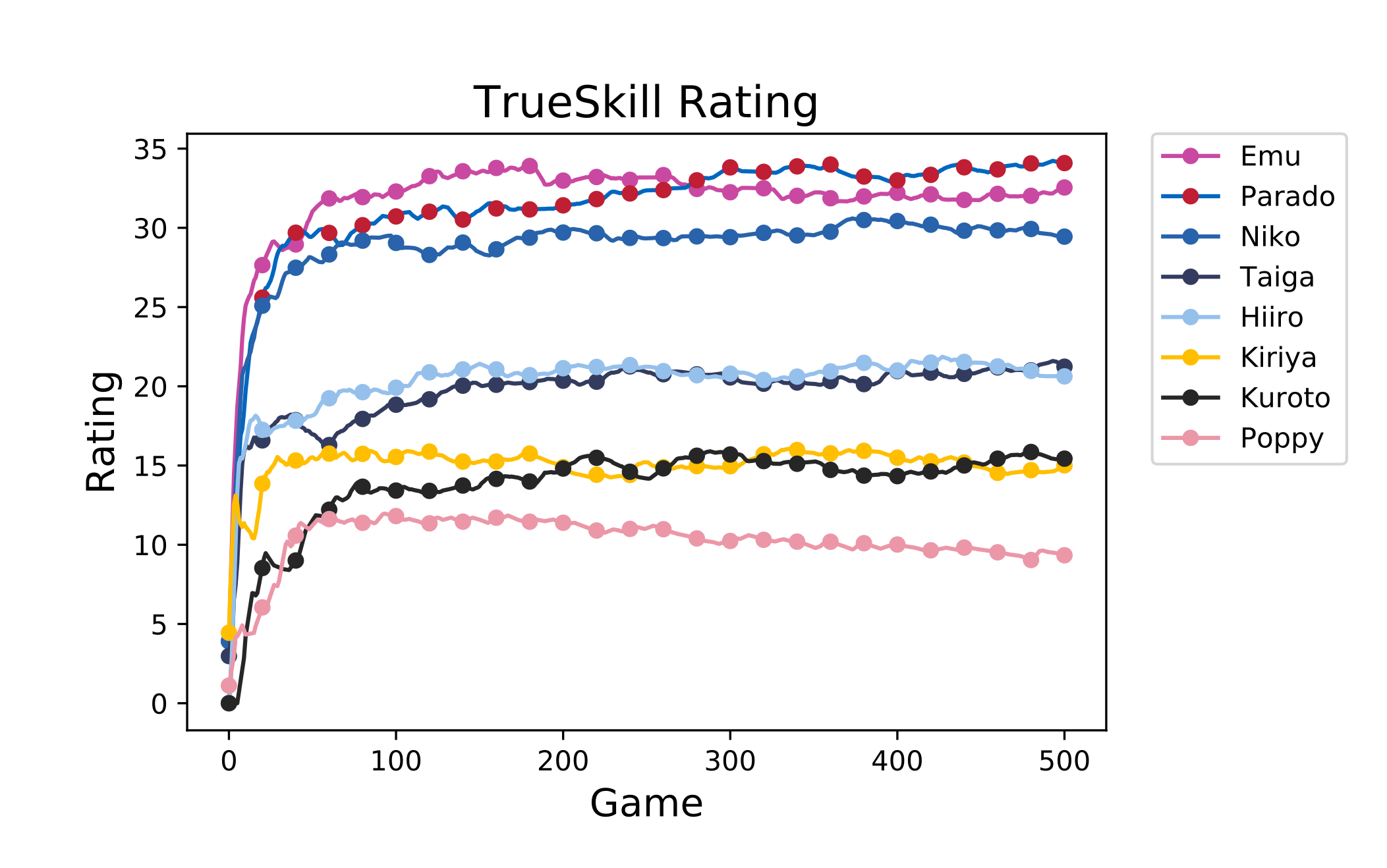
一方で推移は以下のようになりました。 こちらも 5 点移動平均で平滑化して示しています。
見てのとおり、Elo レーティングにくらべて爆速でアプリをデプロイする方法収束しているのが分かります。 最初の数十ゲームでもうある程度の位置が定まっていますね。 これは確かに「収束が早い」と謳うだけのことはあります。
日本プロ野球リーグをレーティングしてみる
いつまでも夢に逃げているとワカメを冷まされるので、いよいよ現実の世界に目を向けてみましょう。
ちょうど最近プロ野球の公式戦が終了いたしましたので、今年度の公式戦データ(セパ交流戦含む)から 12 球団をレーティングしてみましょう。 そんなデータ出したら殺されるのでは?
ちなみにセ・リーグとパ・リーグの 2019 年度公式順位は以下のようになっています。
| 順位 | チーム | 勝 | 敗 | 分 | 勝率 | ゲーム差 |
|---|---|---|---|---|---|---|
| 1 | 巨人 | 77 | 64 | 2 | .546 | 0.0 |
| 2 | DeNA | 71 | 69 | 3 | .507 | 5.5 |
| 3 | 阪神 | 69 | 68 | 6 | .504 | 6.0 |
| 4 | 広島 | 70 | 70 | 3 | .500 | 6.5 |
| 5 | 中日 | 68 | 73 | 2 | .482 | 9.0 |
| 6 | ヤクルト | 59 | 82 | 2 | .418 | 18.0 |
| 順位 | チーム | 勝 | 敗 | 分 | 勝率 | ゲーム差 |
|---|---|---|---|---|---|---|
| 1 | 西武 | 80 | 62 | 1 | .563 | 0.0 |
| 2 | ソフトバンク | 76 | 62 | 5 | .551 | 2.0 |
| 3 | 楽天 | 71 | 68 | 4 | .511 | 7.5 |
| 4 | ロッテ | 69 | 70 | 4 | .496 | 9.5 |
| 5 | 日本ハム | 65 | 73 | 5 | .471 | 13.0 |
| 6 | オリックス | 61 | 75 | 7 | .449 | 16.0 |
野球見ていないマンゆえ贔屓球団とかはないので、この結果を見ても特に感慨がわかないのが残念です。 あえていうなら、DeNA になる前の横浜はひどかったという噂を聞いたことはあるので、いまは上位に食い込んでいるのが面白いなってくらいですかね……。 一応故郷に最も近いのは日ハムです。
ただ、勝率を見ていくと、もちろん順位が付く程度の差はできていますが、たとえばチェスの強い人と初心者レベルの差という程のものはできていない、割と拮抗している8リーグだなあという感じですね。 これはうまくレーティングできるか不安です。
なにはともあれレーティングしてみましょう。 2019 年度の公式戦のデータはこちらに用意しました。 NPB 公式サイトからシコシココピペして作りましたがクッソ面倒でした。 API とか探したらありませんかね?
環境はほぼ初期のまま、引き分け確率のみ過去 3 年度の合計試合数と合計引き分け数から算出して使用します。 こちらにコードを置いておきます。 引き分け数 CSV は一応ここにおいておきますがこれいる?
結果は以下のようになりました。
| チーム | TrueSkill | 公式順位 | 勝 | 敗 | 分 | 勝率 |
|---|---|---|---|---|---|---|
| 西武 | 23.932 | パ 1 位 | 80 | 62 | 1 | 0.563 |
| ソフトバンク | 23.083 | パ 2 位 | 76 | 62 | 5 | 0.551 |
| 楽天 | 22.884 | パ 3 位 | 71 | 68 | 4 | 0.511 |
| 阪神 | 22.801 | セ 3 位 | 69 | 68 | 6 | 0.504 |
| 巨人 | 22.726 | セ 1 位 | 77 | 64 | 2 | 0.546 |
| ロッテ | 22.714 | パ 4 位 | 69 | 70 | 4 | 0.496 |
| DeNA | 22.492 | セ 2 位 | 71 | 69 | 3 | 0.507 |
| 中日 | 22.456 | セ 5 位 | 68 | 73 | 2 | 0.482 |
| 広島 | 22.362 | セ 4 位 | 70 | 70 | 3 | 0.500 |
| オリックス | 22.067 | パ 6 位 | 61 | 75 | 7 | 0.449 |
| 日本ハム | 21.979 | パ 5 位 | 65 | 73 | 5 | 0.471 |
| ヤクルト | 21.395 | セ 6 位 | 59 | 82 | 2 | 0.418 |
野球を見ている皆さん的にはこれは直感に即した結果でしょうかね?
交流戦は全体に比べると数が少ないので、セパ横断順位の信憑性はあんまないと思います。 しかし、リーグ単位で見ても公式順位との入れ替わりがいくつかあるのが見て取れます。 特に阪神はセ・リーグ 3 位にもかかわらずセ・リーグ優勝の巨人を抜いてトップに躍り出ています。
「単に勝率のみを見るのではなく、どれほど強い相手に勝ったかを見る」のがレーティングですが、ランダムマッチングのゲームと違い対戦機会が計画されて平等になっているのがプロ野球ですから、「弱い相手ばっかり選んでるから」みたいなのは発生し得ないはずです。
考えられる可能性としては……単にコピペしただけでちゃんと試合結果を精査したわけではないので推測なのですが、「巨人や DeNA のような成績の良いチームに対する勝率が良かった説」があります。 逆に巨人や DeNA の下位陣相性が悪い説もあります。 やきうのお兄ちゃんたち、実際はどうでした?
レーティングは極めて単純な仮定をおいているところがあり、「A さんが B さんに 2 勝 1 敗、B さんが C さんに 3 勝 2 敗ならば、A さんは C さんに $\frac{2}{1} \times \frac{3}{2} = 3$ 倍の勝利を上げる(4 戦して 3 勝 1 敗)だろう」みたいな感じです。 しかし実際の勝負には相性があることがしばしばあり、C さんが A さん相手だと妙に強かったりするわけです。 こういった影響を小さくするためにも、レーティングでは「なるべく多くのプレイヤープールで、かつ同じ相手とばかり戦わない」ことが精度上昇のためにも重要だったりするわけです。 今回とりあげたプロ野球は、プレイヤープール 12 球団と少なく、さらに交流戦があるとはいえリーグが 2 種に分断されているのであまり良い例ではなかったかもしれませんね。 ぶっちゃけ IIDX のアリーナモードとかレーティングしたいけど KONAMI しか試合データ持っていない。
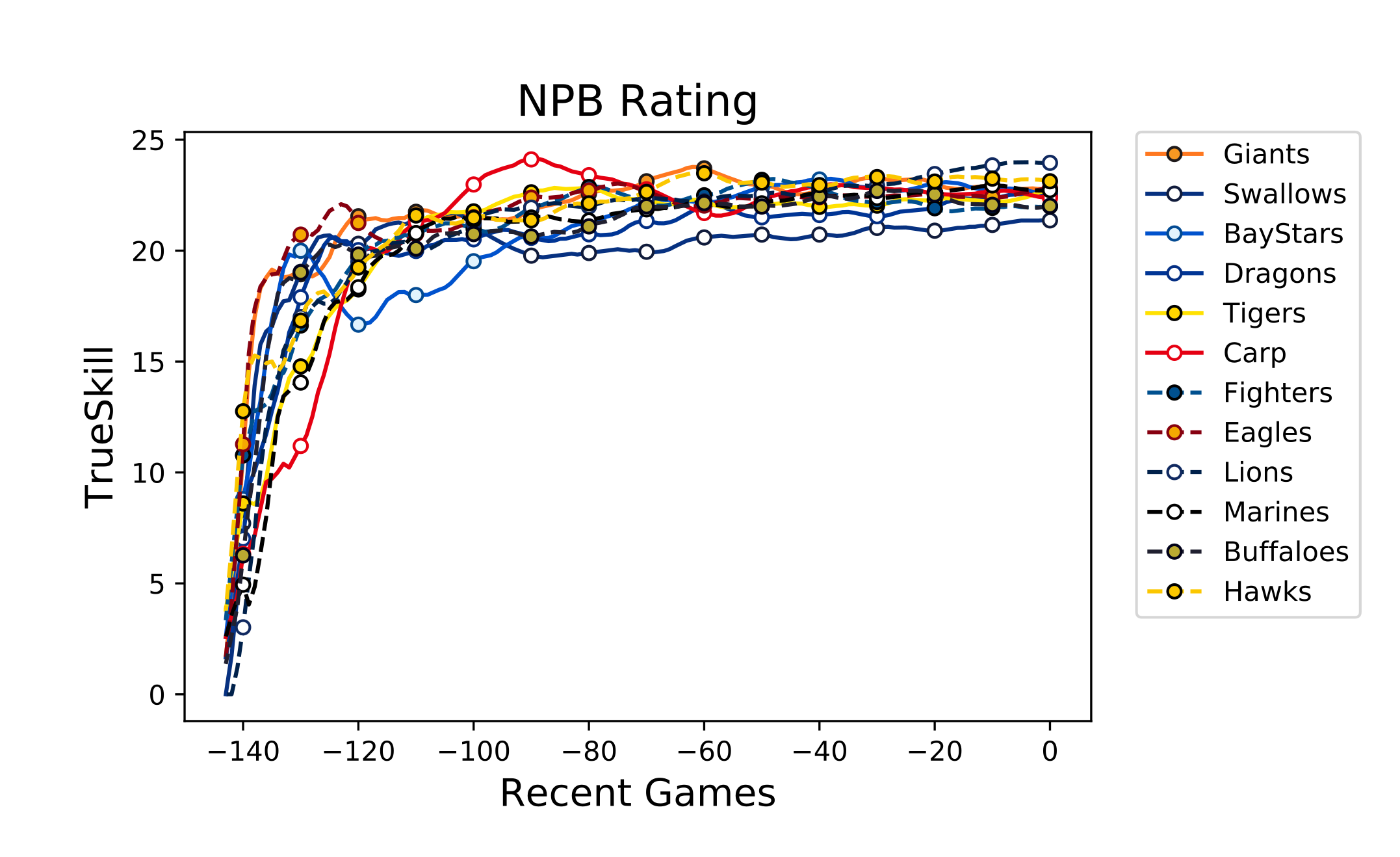
ちょっと脇道にそれ過ぎましたので、推移のグラフでも貼っておきましょう。 例によって 5 点移動平均です。
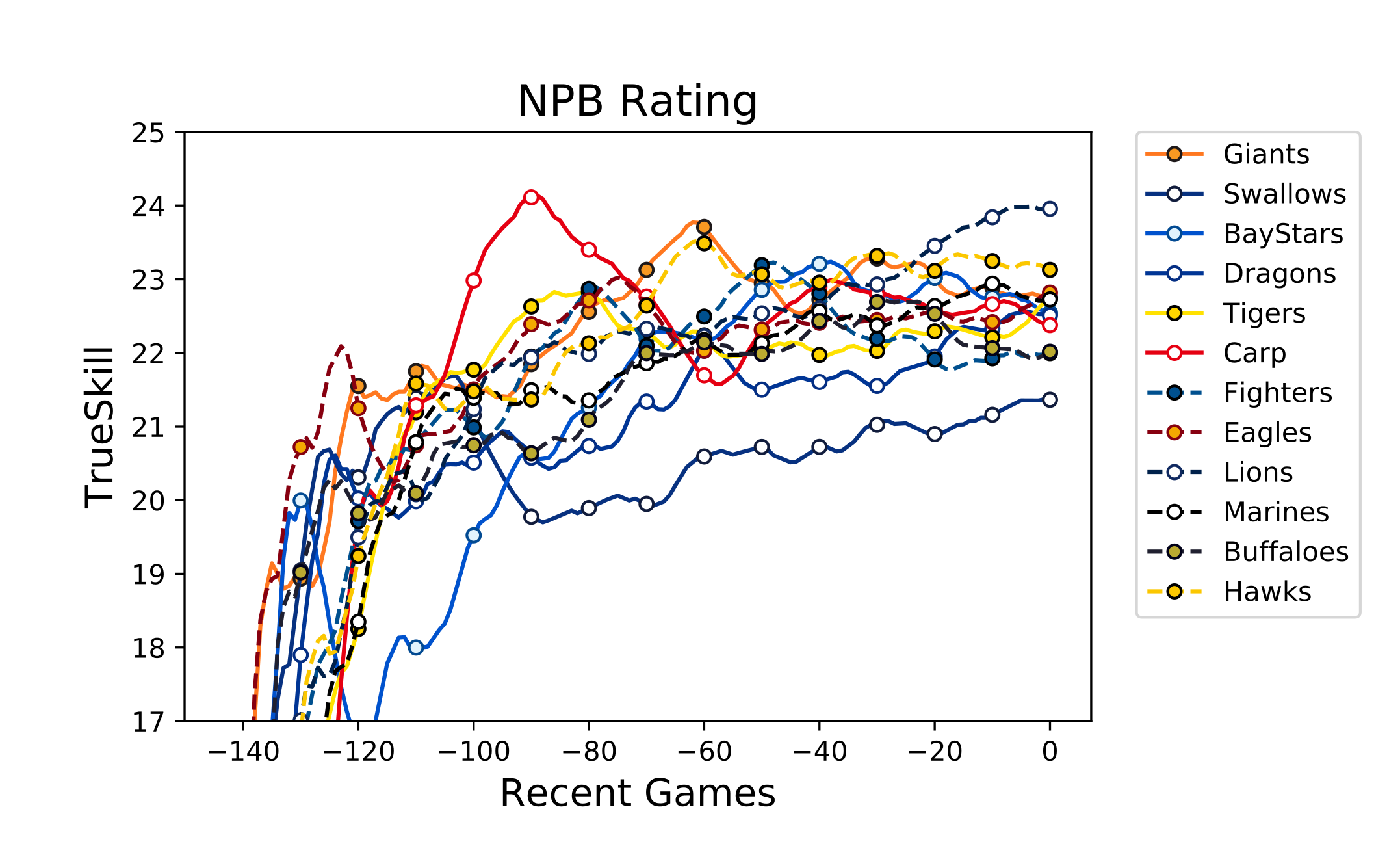
……団子状態過ぎてよくわかりませんね。 $17 \leq y \leq 25$ の範囲だけ拡大してみましょう。
まだ多少見えづらいですがだいぶマシかな? つかチームカラーが似たりよったり過ぎて区別つきづらいんですが……。
パッと見て目立つのは 90 試合前あたりから広島が思いっきり落ち込んでいるところですね……。 今年広島は交流戦で**「こいついっぱい貯金持ってるンゴwww」された**らしいのでそれかもしれません。
あと、横浜は今年セ 2 位となりましたが、立ち上がりはかなり遅かったようです。
最後に、各チームごとの勝率も貼っておきます。 マジで殺されるぞ。
| ○\● | 巨人 | ヤクルト | DeNA | 中日 | 阪神 | 広島 | 日本ハム | 楽天 | 西武 | ロッテ | オリックス | ソフトバンク |
| 巨人 | - | 58.7% | 51.6% | 51.9% | 49.6% | 52.5% | 55.0% | 49.1% | 42.0% | 50.2% | 54.5% | 47.8% |
| ヤクルト | 41.3% | - | 42.9% | 43.1% | 40.9% | 43.7% | 46.3% | 40.4% | 33.7% | 41.5% | 45.8% | 39.1% |
| DeNA | 48.4% | 57.1% | - | 50.3% | 48.0% | 50.9% | 53.4% | 47.5% | 40.4% | 48.6% | 52.9% | 46.2% |
| 中日 | 48.1% | 56.9% | 49.7% | - | 47.7% | 50.6% | 53.2% | 47.2% | 40.2% | 48.3% | 52.7% | 45.9% |
| 阪神 | 50.4% | 59.1% | 52.0% | 52.3% | - | 52.9% | 55.4% | 49.5% | 42.4% | 50.6% | 54.9% | 48.2% |
| 広島 | 47.5% | 56.3% | 49.1% | 49.4% | 47.1% | - | 52.6% | 46.6% | 39.6% | 47.7% | 52.1% | 45.3% |
| 日本ハム | 45.0% | 53.7% | 46.6% | 46.8% | 44.6% | 47.4% | - | 44.1% | 37.2% | 45.2% | 49.5% | 42.8% |
| 楽天 | 50.9% | 59.6% | 52.5% | 52.8% | 50.5% | 53.4% | 55.9% | - | 42.9% | 51.1% | 55.5% | 48.7% |
| 西武 | 58.0% | 66.3% | 59.6% | 59.8% | 57.6% | 60.4% | 62.8% | 57.1% | - | 58.2% | 62.4% | 55.8% |
| ロッテ | 49.8% | 58.5% | 51.4% | 51.7% | 49.4% | 52.3% | 54.8% | 48.9% | 41.8% | - | 54.3% | 47.6% |
| オリックス | 45.5% | 54.2% | 47.1% | 47.3% | 45.1% | 47.9% | 50.5% | 44.5% | 37.6% | 45.7% | - | 43.3% |
| ソフトバンク | 52.2% | 60.9% | 53.8% | 54.1% | 51.8% | 54.7% | 57.2% | 51.3% | 44.2% | 52.4% | 56.7% | - |
いま示したのは既知のデータに基づく勝敗比ではなく、未知の試合に対する勝利確率ということになります。 まあ、あんまり参考にならないとは思いますが……。 ともあれ、レーティング最上位の西武対レーティング最下位のヤクルトでもそこまで絶望的な数値になっていないというところを見ると、やっぱり拮抗した良いリーグです。 野球見てみようかな?
よくばりセット
今回使用したスクリプトやデータを固めたものをここに置いておきました。
Notebook 形式なので JupyterLab などをご用意して頂く必要があります。
まとめ
いかがでしたか?(定型文)
今回使用したのは Python 実装でしたが、どうも様々な言語にフォークされているようなので、あなたが使いたい言語での実装も見つかるかもしれませんし見つからないかもしれません(あいまい)。
私が今回の記事で伝えたかったのは、「既存の Elo レーティングとかにくらべて TrueSkill の理論は、腰を据えて読まないとわからないしそもそもある程度の前提知識がないと厳しいのは確かだけど、使うだけなら脳死でメソッド叩くだけで使えるし性能もいいからめっちゃ使ってほしい」ということです。
Elo を利用した記事は Qiita にも多い9ので、これから TrueSkill でレーティングする記事も増えてほしいと思います。
あと、レーティングといえば Glicko とかも Elo より性能よくて自分で実装するのも難しくないのでオヌヌメです。
Elo 以外のレーティングもっと流行れ!
-
チームとはいっても、テレビで放送されているプロスポーツのような「チームの構成員がほぼ一定で、ある選手がゲーム単位の短いスパンでチームを変更しない」チームの場合、チームそのものをプレイヤーとして扱うのが理にかなっています。 ここでいうチーム戦とは、例えば Splatoon のようなマッチングしたプレイヤーをランダムにチームに振り分けて行われるようなゲームに向いています。 ↩
-
$\phi_{\mu, \sigma^2}$ は確率密度関数一般のことではなく正規分布のことなのですが、わかりやすさ重視でここにねじ込んでしまいました。 YURUSHITE。 ↩
-
具体的には 99.73% 程度。 ↩
-
実際には、更新前にごく少量の σ が与えられるため、常に減少し続けるわけではありません。 成長やブランクによるスキルの変化を許容できるということだと思います。 ↩
-
そもそもレーティングの研究はチェスから始まりました。 ↩
-
そして、これがレーティングという仕組みが本質的に抱えるどうしようもない弱点でもあります。 たとえば、あるリーグのプレイヤーがもつレーティングと、それとは別のリーグに参加しているプレイヤーがもつレーティングは、レーティングの仕組みが同じだったとしても比較できません。 ↩
-
今回のスムージングでは、端を端点の値で埋めてから
mode='valid'で畳み込んでいます。mode='same'でも良いのでしょうが、まあ「しゅみです」ということで。 ↩ -
この辺は野球見ている人と温度差があると思います。 レーティング視点でということです。 ↩
-
車輪の再発明系の記事だと TrueSkill は難しいと思いますが。 ↩