ここに実力の分からない、Aさん、Bさん、Cさんがいるとしましょう。
Aさん、Bさん、Cさんが、ある勝負で試合をしていきます。3人全員で試合をすることもあれば、2人で試合をする時もあれば、AさんとBさんがタッグを組んで、Cさんと試合をすることもあるとします。ようは何でもありです。
我々が知ることができるのは、ただ各試合の勝敗(3人の場合は順位)だけです。
その数多の歴戦の結果から、Aさん、Bさん、Cさんの実力を数値化したい時、どのように数値化するのが適切でしょうか。
その問いに答えてくれる、一つの強力な手法が、そう、 TrueSkill です。
さて、Machine Learning Advent Calendar 2016の1日目です。
折角の初日なので、機械学習入門についてでも書こうかと迷いましたが、どこまで書くべきか難しい上に、体系的に述べられるほど専門家では決してなく、世には分量こそ多かれ良い入門書も数あるので、あまり日本語での詳細な説明の見当たらないTrueSkillを紹介することにしました。
なぜTrueSkillを紹介しようと思ったかというと、TrueSkillではベイズの定理・グラフィカルモデル・ガウシアン・近似計算など機械学習での多くの基本的な技術・知識が用いられているため、機械学習を学ぶ上での一つのいい教材となる具体的なアルゴリズムだと思ったからです。
TrueSkill以外にもそういった(教材たりうる)アルゴリズムはいくらでもあると思いますが、最初に述べたような実世界での身近な分かりやすい問題に活用されている点も良いかなと考えました。
なお、本文中の斜字で書いてある部分は、注や参考など読み飛ばしても構わない補足事項を示しています。
注:ハワイに滞在しているため、ハワイ時間の12/1に投稿です(大嘘)。本Advent Calendar作成者かつ初日担当ながら最初から投稿遅れてしまい本当に申し訳ありません。言い訳をするわけではありませんが、書き出した時はまさかここまで長くなると思っておらず、明らかに一記事にまとめるべきでない内容と量ですので、Advent Calendar終了後に、内容ごとに複数の記事に分割する予定です。また、最後の方はまだ抜けている点多いため随時加筆・修正していきます。
TrueSkillとは
TrueSkillはMicrosoftが2005年頃に開発したレーティングアルゴリズムです。つまり、プレイヤーたちの腕前・技量を結果の勝敗に基づいて数値化することを目指します。
Microsoftは実際にこのアルゴリズムを、Xbox Live上のゲーム、例えばHalo 2などに活用していて、よりプレイヤーが楽しめるよう、より均等な強さのプレイヤー同士をマッチングできるよう、各プレイヤーの強さをTrueSkillを用いて数値化しています。
このようなレーティングアルゴリズムと呼ばれるものは他にも昔からいくつか存在していて、特にElo ratingと呼ばれるものが有名で、例えば国際チェス連盟ではそのElo ratingに基づいて各チェスプレイヤーの実力を数値化しランキングとして公表しています。
それでは、Microsoftがなぜわざわざこのような新しいアルゴリズムを考案したのかというと、それがつまりTrueSkillが他の一般的なレーティングアルゴリズムと比べて異なっている点、あるいは、優れている点ともなるわけですが、主に以下の2つの理由があります。
- 単なる1対1の試合だけでなく、複数人が同時に対戦する試合にも対応できる(マリオカートを思い浮かべると分かりやすい)
- チーム対チームの試合の勝敗の結果から各個人をレーティングすることにも対応できる(スプラトゥーンを思い浮かべると分かりやすい)
なお、TrueSkillもElo ratingも単なる勝率だけで強さを決定するわけではなく、同じ勝ち負けでもより強い人に勝った人は強く、より弱い人に負けてしまった人は弱いという考えが根底にあります(極めて自然で直感的な前提だと思います)。
注:およそどんな勝負事でも、プレイヤーの強さがこのようなレーティングに基づく完全な全順序になっていることは稀で、個々の対戦相手に対する得手不得手(相性)など当然存在します。従ってレーティングはあくまで目安ですが、実際に適用されている問題では、真の強さに対して何もないよりは情報量があり、なおかつ、TrueSkillを応用すれば、個別の勝負事に特化したより正確なレーティングシステムを作成することも可能でしょう。
前提とする知識
誰でも分かるとタイトルに書いてありますが、直ちに誰でも分かるわけではありません。つまり、以下に書いた事柄については既知として話を進めていきます。これは、言うまでもなく、決して読者をふるい分けたいわけではなく、以下の事柄についてはここで説明しなくとも他に分かりやすい教材が既に豊富にあるからです。逆に言えば、以下の事柄について知っている人ならば誰でも分かるように心がけて説明をしているつもりではありますが、もしかすると漏れがあるかもしれません。
・確率の初歩
確率密度関数・累積分布関数・同時確率・条件付き確率・周辺確率など。
・大学初等レベルの微分積分
ガウス分布の0次、1次、2次のモーメントを自力で計算できる(あるいは計算方法を思い出しておく)と数式を追いやすいと思います。
今後の流れ
前置きが長かったですが、説明はもっと長くなるので、初めにどのような順序で説明を進めていくかをお話します。
TrueSkillのアルゴリズムを理解するためには、以下の知識が必要になります。
- グラフィカルモデルとグラフィカルモデル上での推論
- ガウス分布とガウス分布同士の種々の計算
- 切断されたガウス分布のガウス分布による近似
この内、最も基本となる、土台となる「グラフィカルモデルとグラフィカルモデル上での推論」についてだけ、どうしても長くなるので、初めに分けて説明していきます。
それ以外の事項は、TrueSkillを説明する時に必要になった段階でそれぞれ説明していきます。
既に、ファクターグラフやBPアルゴリズムについて知っている方はTrueSkillまでジャンプできます。
説明が長いため、迷いそうになるかも知れませんが、その時はTrueSkillのアルゴリズムは上記したたった3つの知識によって構成されているということを思い出して下さい。
グラフィカルモデルとグラフィカルモデル上での推論
ベイズの定理
TrueSkillに限らず、およそ機械学習に関するアルゴリズム・理論を勉強する上で、ベイズの定理を外すことはできません。ほとんどの機械学習の入門書ではイントロダクションか次の章にはベイズの定理を紹介していると思います。
ベイズの定理は以下のように確率の基本定理から導くことができます。
\begin{align}
P(X,Y) &= P(X)P(Y|X) \\[5pt]
&= P(Y)P(X|Y) \\
\end{align} \\[25pt]
\Rightarrow P(X|Y) = \frac{P(Y|X)P(X)}{P(Y)}
特に$Y$が観測した事象であるとき、$P(X)$を事前確率、$P(X|Y)$を事後確率と呼びます。
具体例
式だけではイメージが掴みづらいと思いますので、簡単な具体例で見てみましょう。
ホテルのレストランで殺人事件が起こり、犯人を見つけたいとしましょう。$X$を犯人を表す確率変数とします。警察の捜査により、アリバイのない容疑者はレストランのシェフか同じホテルで働くアルバイトにまで絞り込めたとしましょう。
レストランのシェフは、真面目な働きぶりで有名で、周りの人からの信頼も厚いです。
一方、アルバイトは、普段の素行はあまり良くなく、若い頃は不良でしばしばトラブルを起こしていたことが知られています。
この時、犯人、つまり$X$、がシェフである確率は20%、アルバイトである確率は80%であるとしましょう。
| 犯人 | |
|---|---|
| シェフ | 20% |
| バイト | 80% |
| 計 | 100% |
これがここで言う事前確率です。
その後、捜査が進み、凶器が包丁であると判明したとします。これが観測された事象、$Y$に当たります。
さて、シェフとアルバイトのそれぞれについて、入手の容易さから凶器として使用する確率が以下のように分かっているとします。
| 凶器\犯人 | シェフ | バイト |
|---|---|---|
| 包丁 | 80% | 30% |
| バール | 10% | 50% |
| 毒薬 | 10% | 20% |
| 計 | 100% | 100% |
これが、$P(Y|X)$に当たり、尤度と呼ばれます。
以上の情報から、ベイズの定理を用いて、事後確率、$P(X|Y)$を求めることができます。
なぜなら、確率の基本定理より、
$P(Y)=\sum_{X}P(X,Y)=\sum_{X}P(Y|X)P(X)$
が成り立ち、
$P(Y=包丁|X=シェフ)P(X=シェフ)= 0.8 \times 0.2 = 0.16$
$P(Y=包丁|X=バイト)P(X=バイト)= 0.3 \times 0.8 = 0.24$
で、結局、
$P(Y=包丁) = 0.4$
であることが分かり、
$P(X=シェフ|Y=包丁)= 0.16/0.4 = 0.4$
$P(X=バイト|Y=包丁)= 0.24/0.4 = 0.6$
となります。もともと事前確率では$P(X=シェフ)=0.2$だったため、凶器が判明したことにより、シェフが犯人である確率(事後確率)が20%から40%に変わりました。
このように観測された事象によって確率が変化したとみなせるため、事前確率、事後確率と呼ばれます。
注:そもそも初めの事前確率も警察の捜査によって分かったものなのでこれは事後確率で、真の事前確率は、およそ全ての人が等確率で犯人たりうるものではないのかと思う人もいるかも知れません。それ自体は全く正しい考え方ですが、事前・事後というのはあくまでその時考慮に入れる観測した事象と比較して、事前か事後かという相対的なものなので、同一の確率分布でも見方によって事前確率にも事後確率にもなり得ます。
上で計算したように、$P(Y)$は全ての$X$についての$P(Y|X)P(X)$の総和で計算できますが、その計算が困難なこともあります。しかし、$P(Y)$の値は$X$に依らないため、2つの$X=X_1,X_2$に対して、
$P(X_1|Y) : P(X_2|Y) = P(Y|X_1)P(X_1) : P(Y|X_2)P(X_2)$ ($X=$ を略)
のように、事後確率の比率は$P(Y)$の計算をすることなしに導出することができます。
実際、上の式を使うと、
$P(X=シェフ|Y=包丁) : P(X=バイト|Y=包丁) = 0.16 : 0.24$
で、最終的に導出した正確な事後確率、$0.4 : 0.6$と果たして一致します。
その意味で、ベイズの定理は以下の様に書かれることもしばしばあります。
P(X|Y) \propto P(Y|X)P(X)
グラフィカルモデル
上記のような二変数の例では、事前確率、尤度について、表を用いて全ての場合の確率を書き下し、見ることができました。しかし、変数の数が3つ、4つと増えるにつれて、確率変数が取りうる全ての場合の数は、変数の数に合わせて指数的に増えていくことが分かります(例えば、各変数が2つの値を取り、$n$個確率変数が存在すると、全ての場合の数は$2^n$ある)。このようなケースでは、もはや全ての場合の確率を記述することは現実的ではありません。
一方で、普段我々が機械学習で考えるモデルでは、また、現実の問題でも、往々にして全ての確率変数がそれぞれ依存しあっていることはなく、ある確率変数とある確率変数が独立であったり、または条件付き独立であったりします。以下の具体的な例で見るように、確率変数の独立性を最大限活用することで、確率計算の計算量を抑えることができます。ゆえに、確率変数の依存関係を理解することは重要で、それをグラフとして可視化したものがグラフィカルモデルと呼ばれるものです。
具体例
再び具体例を交えて見ていきましょう。
グラフィカルモデルでは、確率変数をノード(節点)、依存関係をエッジ(枝)として確率分布をグラフの形で表現します。
例1
まずは極端な例から見ましょう。確率分布内の全確率変数が互いに独立な以下の確率分布を考えます。
$P(A,B,C)=P(A)P(B)P(C)$
注:上の分解は当然常に成り立つものではありません。確率の性質より、
$P(A,B,C)=P(A)P(B|A)P(C|A,B)$や$P(A,B,C)=P(A,B|C)P(C)$などは常に成り立ちます。
この時、この確率分布を表すグラフィカルモデルは以下の様になります。

各確率変数は互いに独立であるため、一切エッジで結ばれていません。
この時、確率変数$A,B,C$がそれぞれ$k$個の状態を持つとした時、普通であるならば、確率分布$P(A,B,C)$を記憶するためには$k^3$個の状態の確率を覚える必要があります。しかし、今$A,B,C$は互いに独立であり、$P(A,B,C)=P(A)P(B)P(C)$が成り立つため、$P(A,B,C)$を覚えるためには、$P(A), P(B), P(C)$を記憶すれば十分であることが分かります。これは$3k$個の状態しかなく、$k$が大きい時、$k^3$と比べてずっと小さく、独立であるという条件がいかに記憶量の点で有効に働くか分かると思います。
また、それだけでなく、$P(A,B,C)$から周辺確率$P(A=a)$を求めたい時、
$P(A=a)\hspace{2pt}=\hspace{2pt}\sum_{B} \sum_{C} P(A=a,B,C)$
が成り立つので、普通であるならば、$k^2$に比例した計算量が必要になります。しかし、互いに独立である場合、上述したように$P(A,B,C)$のために自然に$P(A)$を保持しているため、$k$に関係のない(定数の)計算量で済み、計算量の上でも大きな恩恵があることが分かります。
この例では全ての確率変数が独立という極端な例でしたが、次の例で示すように、$A$と$B$のみが独立という場合でも計算量は確かに減少します。
例2
次に以下の確率分布を考えます。
$P(A,B,C)=P(C|A,B)P(A)P(B)$
この確率分布を表すグラフィカルモデルは以下の様になります。
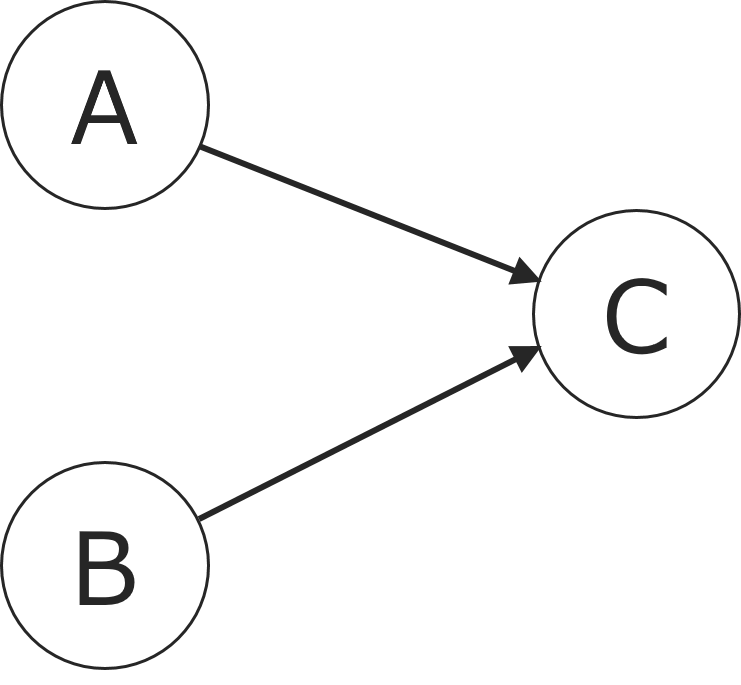
確率変数$C$の確率分布が、$A$と$B$の条件付き確率という形で現れ、$A$と$B$に依存しているため、$A, B$から$C$にエッジが結ばれていることが分かります。
この時、エッジの方向は重要で、エッジの方向を変えた以下のグラフィカルモデルは、

$P(A,B,C)=P(A|C)P(B|C)P(C)$という全く別の確率分布を表します。
さて、元の確率分布に戻ると、確率の性質より$\sum_{C}P(C|A,B)=1$なので、
$P(A,B)=\sum_{C}P(A,B,C)=\sum_{C}P(C|A,B)P(A)P(B)=P(A)P(B)$
となり、$A$と$B$は独立であることが分かります。
参考:しかしながら一度$C$を観測してしまうと、$A$と$B$の独立性はもはや成り立たなくなることが分かります。一方で、エッジの方向を変えたグラフでは、$A$と$B$は通常独立ではないものの、$C$を観測すると独立になることがわかります。この時、$A$と$B$は、$C$による条件付き独立であると言います。
例1にならって、周辺確率$P(A=a)$を計算してみると、
$P(A=a)\hspace{2pt}=\hspace{2pt}\sum_{B} \sum_{C} P(A=a,B,C) = P(A=a)\sum_{B}P(B)\sum_{C}P(C|A,B) = P(A=a)\sum_{B}P(B)$
となり、これは$k$に比例した計算量が必要で、やはり$k^2$から減少していることが分かります。
例3
最後に与えられたグラフィカルモデルから確率分布を導くことを考えます。
以下のグラフィカルモデルが示す確率分布はどのようなものでしょうか。

今まで見てきた例からも分かる通り、親を持たないノードは事前確率を持ち、エッジはそのまま条件付き確率となるので、上のグラフィカルモデルは、
$P(A,B,C,D,E,F)=P(A)P(B)P(D|A,B)P(C)P(E|C,D)P(F|D)$
という確率分布を表しています。
このように、確率分布の分解をグラフィカルモデルとして表すこともできれば、その逆も容易に可能なことが分かります。
まとめ
今までの例で見てきたように、記憶量や計算量の観点から確率変数同士の独立性などを確かめることが重要で、グラフィカルモデルを用いると確率変数の依存関係が分かりやすく可視化されることが分かりました。
次のセクション以降では、グラフィカルモデルを単なる可視化のためのグラフとして使うだけではなく、メッセージパッシングという仕組みを用いてグラフィカルモデルから直に周辺確率を計算する方法を見ていきます。
参考:今回挙げたような、依存関係に方向があり(有向)、方向に沿ったループがない(非巡回)グラフを特に、ベイジアンネットワークと呼びます。一方で、エッジに方向がない、無向グラフィカルモデルというものもあり、マルコフ確率場 (MRF) と呼ばれます。どちらも基本的な考えや計算は共通していますが、両者が表現しきれる確率変数の依存関係には違いがあります。
ファクターグラフ
少し天下り的ですが、ここで次のセクションの前準備として、ファクターグラフ(因子グラフとも呼ばれる)というものを簡単に紹介します。ファクターグラフは必ず導入しないといけないものではないですが、ファクターグラフで表現すると実際の計算やアルゴリズムが簡素化され、次セクション以降の理解が容易になるというメリットがあります。
ファクターグラフは、グラフィカルモデルの一種で、ノードを変数ノードと関数ノードに分け、確率変数そのものを丸の形の変数ノードで、確率変数の事前確率や条件付き確率などの関数を四角の形の関数ノードで表します。
関数ノードは関数を決定する(関数に含まれる)全ての変数ノードと結ばれ、変数ノードは自然にその変数が寄与する全ての関数ノードと結ばれます。また、関数ノードは必ず変数ノードとのみ結ばれ、変数ノードは必ず関数ノードとのみ結ばれます。
例えば、$P(A,B)=P(A)P(B|A)$のような確率分布の場合、次の様になります。

上で関数と言いましたが、$P(A)$は$A$の値によって$P(B|A)$は$A$と$B$の値によって一意に決まるため、それぞれ$A$の関数、$A$と$B$との関数とみなすことができます。
この時、全体の確率分布(全変数の関数)は全ての関数ノードの積で表されます。
(あるいは、ファクターグラフは積の形に分解される関数を表現するグラフとも言えます。)
先のセクションで見た、
$P(A,B,C,D,E,F)=P(A)P(B)P(D|A,B)P(C)P(E|C,D)P(F|D)$
をファクターグラフで表すと以下の様になります。

同じ様に、分解された各確率分布がそれぞれ関数ノードとして現れています。
既にお気づきかもしれませんが、ファクターグラフでは、前セクションのグラフではあったエッジの矢印(方向)が無くなっています(無向グラフになっている)。なぜなら関数ノードを導入したことで、単にその関数ノードの積で全体の確率分布を一意に表現できるようになったため、エッジの向きは全体の確率分布を表す上で関係が無くなったからです。
次のセクションでは、ファクターグラフを用いることで、グラフ上で確率分布の周辺確率を計算できることを見ます。
グラフィカルモデル上での推論
グラフィカルモデル上での推論と言えば、確率変数の周辺確率を求める事を言います。
例えば、最初のホテルの事件の例では、$P(Y)$の周辺確率を求める、つまり各凶器の使われる確率を求めることができます。そこでもあげた通り、これは確率の基本定理より、$\sum_{X}P(Y|X)P(X)$で求まりますし、$Y=包丁$の時の確率を実際にそこでは計算しました。
ホテルの例では、グラフィカルモデルを考えていませんでしたが、もしグラフィカルモデルで考えていたならばそれ($Y$の周辺確率を求めること)はグラフィカルモデル上の推論と言えます。
何かが観測された上での、条件付きの確率(事後確率)でも良く、例えば、あるグラフィカルモデルで表された$P(A,B,C)$という確率分布で、$B=b$が観測された上で、$A$の周辺確率$P(A|B=b)$を求めることもグラフィカルモデル上の推論に当たります。
この、グラフィカルモデル上での推論には様々なアルゴリズムが存在しますが、最もよく知られているアルゴリズムの一つに確率伝搬法(Belief Propagation, BP)と呼ばれるアルゴリズムがあります。
BPアルゴリズムは一言で言うと、周辺確率の計算をグラフのノード間でメッセージをやり取り(=メッセージパッシング)することで、反復的にグラフ上の全確率変数の周辺確率を計算するものです。従って、
- メッセージの受け渡しによる反復計算アルゴリズムである。
- グラフ上の全確率変数の周辺確率を同時に求める事ができる。
というのがBPアルゴリズムの特徴です。
ただ、BPアルゴリズムはループ(閉路)のないグラフを仮定しているため、今後特に明記した場合を除いて、ループのない無向グラフ(グラフ理論で言うところの「木」)を対象として考えます。
参考:他の推論アルゴリズムとしては例えばある一つの確率変数の周辺確率だけを求めたい時に使えるアルゴリズムも存在します。Variable Eliminationと呼ばれるアルゴリズムはその一つで、計算量こそ同等ですが、BPアルゴリズムと違いループありのグラフを含む任意のグラフに対応できるという利点があります。しかし、TrueSkillを含め、実際の問題ではいくつかの確率変数について同時に周辺確率を求めたい事が多く、またBPアルゴリズムが厳密解を求められないループのあるグラフにそのままBPアルゴリズムを適用しても経験的に大変いい近似解が得られることが多いことが知られています。この場合のBPアルゴリズムを特にloopy BPアルゴリズム呼び、理論的な背景含め活発に研究されているアルゴリズムです。
具体例
さて、BPアルゴリズムがやり取りするメッセージの内容についてですが、決して特殊なものではなく、実際の周辺確率の計算に沿った自然なものです。
それを理解するために、まず幾つかの具体的なグラフ上で実際に周辺確率を計算してみます。
注:BPアルゴリズムを理解する一番手っ取り早い方法は、実際に様々な種類のグラフを書いてそれぞれの確率変数について周辺確率を実際に計算してみることだと思います。多くの入門書に書いてあり、僕も真実だと思うことですが、こういう式計算や式変形は眺めて文章として読んでも何の理解にも繋がりません。実際に手を動かして計算して頭で理解することで、初めて体得できます。
例1
初めに、次のシンプルなファクターグラフを考えます。

これを確率変数$B$について周辺化してみましょう。また、ここでは$D=d$と観測されているとします。
ファクターグラフより、$P(A,B,C,D)=P(A)P(B|A)P(C|B)P(D|C)$で、
\begin{align}
P(B,D=d) &= \sum_{A}\sum_{C}P(A,B,C,D=d) \\[5pt]
&= \sum_{A}\sum_{C}P(A)P(B|A)P(C|B)P(D=d|C) \\[5pt]
&= \biggl(\sum_{A}P(A)P(B|A)\biggr)\biggl(\sum_{C}P(C|B)P(D=d|C)\biggr) ・・ (1)
\end{align}
最後の式変形は、一般に、分配法則より、
$\sum_{a}\sum_{b}f(a)g(b) = \bigl(\hspace{1pt}\sum_{a}f(a)\hspace{1pt}\bigr)\bigl(\hspace{1pt}\sum_{b}g(b)\hspace{1pt}\bigr)$
$\sum_{a}\sum_{b}f(a)g(a, b) = \sum_{a}f(a)\sum_{b}g(a,b)$
が成り立つからです。ここで、下式の右辺は、
$\sum_{a}\Bigl(\hspace{1pt}f(a)\sum_{b}g(a,b)\hspace{1pt}\Bigr)$
と同じ意味です(別の言い方をすれば、$\sum$は積より演算子の優先順位が低い)。
さて、$(1)$の式をよく眺めると、$B$の周辺確率は、最終的に$B$から出ているエッジ毎の計算の積になりそうです。実際、$B$から見て、左にある$A$と右にある$C,D$は、今ループのないグラフを仮定しているため、$B$で分断されており、お互い干渉しあえません。従って、一般に、$P(B)$は何らかの関数$F,G$によって$P(B) = \bigl(\hspace{1pt}\sum_{A}F(A)\hspace{1pt}\bigr)\bigl(\hspace{1pt}\sum_{C}\sum_{D}G(C,D)\hspace{1pt}\bigr)$と表されるはずです。
ゆえに、仮に関数ノード$f$から変数ノード$v$へのメッセージを、$m_{f\rightarrow v}$で表すとすると、
$P(B)=\prod_{f \in n(B)}m_{f\rightarrow B} ・・ (2)$
と書けます。ただし、$n(B)$は$B$と直接接続している(つまり隣接している)全ての関数ノードとします。
例えば、$P(B|A)$から$B$へのメッセージは$(1)$の式で言う所の、$\sum_{A}P(A)P(B|A)$に当たります。
ここで改めて、$(1)$の式を見直すと、各確率変数の総和 ($\sum$) は、その確率変数(の変数ノード)が直接接続している関数ノードのうち、今注目している確率変数(ここでは$B$)に近い方の関数ノードが掛けられた時に、行われていることが分かります。
これは少し考えると自明で、ファクターグラフの定義より、ある確率変数($X$とおく)が現れる関数はその確率変数が直接結びついている関数ノードのみで、注目している確率変数($A$とおく)から見て、$X$が現れる関数ノードより深いところで$X$について総和を取ってしまうと適切に周辺化が行えないため、自然、$A$から見て、最も浅い(近い)関数ノードで総和が行われます。
従って、関数ノード$f$から変数ノード$v$へのメッセージ$m_{f\rightarrow v}$は、$f$に直接接続する$v$を除く全ての変数に関して総和を取ることが分かります。実際、上でに見たように、$P(B|A)$から$B$へのメッセージは$P(B|A)$に直接結びついている$A$に関して総和がされています。
今簡単のため、このグラフの例のように、一つの関数ノードに結びつく変数ノードは高々2つであるとすると(3つ以上の場合は次の例で見ます)、$m_{f\rightarrow v}$は$f$に直接接続されたもう1つの変数ノードを$v'$とし、変数ノード$v'$から関数ノード$f$へのメッセージを$m_{v'\rightarrow f}$とおくと、
$m_{f\rightarrow v} = \sum_{v'} m_{v'\rightarrow f} f(v,v') ・・ (3)$
と書けます。
上のグラフで言う$P(A)$のように、1つの変数ノードとのみ結ばれている場合、送られるメッセージはその関数自体となり、関数ノードに結ばれたある変数ノードが観測されている場合は、$P(D=d|C)$のように、その値で固定された関数となります。
最後に、変数ノードから関数ノードへのメッセージは、その変数ノードより深い(下の)変数に関して全て周辺化されているべきなので、つまりそれはメッセージを送る関数ノードがないとした場合の、その変数ノードでの周辺確率に他ならず、式$(2)$で行った議論は一般性を失うことなく他の確率変数についてもそのまま成り立つので、つまり、周辺確率は、式$(2)$より、メッセージを送る関数ノード以外の全ての関数ノードからメッセージの積になることが分かります。
$m_{v\rightarrow f} = \prod_{f' \in n(v)\backslash f} m_{f'\rightarrow v} ・・ (4)$
ただし、$n(v)\backslash f$は$f$を除く$v$の全ての隣接した関数ノードで、他に隣接した関数ノードがない場合は、確率の性質より周辺確率$\sum_{X}P(X)$は$1$になるので、メッセージも$1$になります。
式$(2),(3),(4)$より全てのノード間のメッセージと、そして、確率変数の周辺確率が計算できるはずなので、実際に計算してみましょう。
$P(B,D=d)$をまた求めたいとして、まず$B$の左側から、
- $P(A)$から$A$へのメッセージは、上述したように$P(A)$
- $A$から$P(B|A)$へのメッセージは、$(4)$より$P(A)$
- $P(B|A)$から$B$へのメッセージは、$(3)$より$\sum_{A}P(B|A)P(A)$
次に、$B$の右側についても、
- $D$は観測されているので、$P(D|C)$から$C$へのメッセージは、$P(D=d|C)$
- $C$から$P(C|B)$へのメッセージは、$(4)$より$P(D=d|C)$
- $P(C|B)$から$B$へのメッセージは、$(3)$より$\sum_{C}P(C|B)P(D=d|C)$
最後に、$P(B,D=d)$は$(2)$より、$P(B|A)$から$B$へのメッセージと、$P(C|B)$から$B$へのメッセージの積であるため、$P(B,D=d)=\bigl(\sum_{A}P(A)P(B|A)\bigr)\bigl(\sum_{C}P(C|B)P(D=d|C)\bigr)$と確かに求まっています。
BPを最初に紹介した時に、BPでは全ての確率変数について同時に周辺化できると言いました。
実際にこのまま$P(A,D=d)$を求めてみましょう。$P(A,D=d)$を求めるためには後、$P(B|A)$から
$A$へのメッセージが分かればよく、
- $P(B)$から$P(B|A)$へのメッセージは、$(4)$より$\sum_{C}P(C|B)P(D=d|C)$
- $P(B|A)$から$A$へのメッセージは、$(3)$より$\sum_{B}P(B|A)\sum_{C}P(C|B)P(D=d|C)$
$P(A)$から$A$へのメッセージは$P(A)$だったので、結局、
$P(A,D=d)=P(A)\sum_{B}P(B|A)\sum_{C}P(C|B)P(D=d|C)$
と求まりました。
検算のために$P(A,D=d)$を直接計算すると、
\begin{align}
P(A,D=d) &= \sum_{B}\sum_{C}P(A,B,C,D=d) \\
&= \sum_{B}\sum_{C}P(A)P(B|A)P(C|B)P(D=d|C) \\
&= P(A)\sum_{B}P(B|A)\sum_{C}P(C|B)P(D=d|C)
\end{align}
となり、一致することが確かめられます。
さて、このまま全ての確率変数について周辺確率を求めるためには、$(2)$より変数ノードに向く全てのメッセージが求まればよく、グラフの性質上どのエッジも(関数ノードと変数ノードへの)2つの方向のメッセージしか持ちえないので、適当な変数ノードを根(親)として、最も深い変数ノードたちから根に向かってメッセージを計算していき、根までたどり着いたら今度は逆方向にメッセージを計算していくことで、全てのノードについて両方向のメッセージが分かります。
従って、BPアルゴリズムではグラフ上を2 path(2回)メッセージパッシングすれば、グラフ上の全ての確率変数についての周辺確率が求まることが分かります。
例2
例1は、関数ノードに高々2つの変数ノードしか結びついていないグラフでした。ですので、ここでは関数ノードに3つ以上の変数ノードが結びついている(一般のグラフの)場合について考えます。
幸い、$(3)$の式が少し変わるだけの修正で済みます。
以下のファクターグラフについて考えましょう。(分かりやすさのために関数ノードに名前を付けています。)
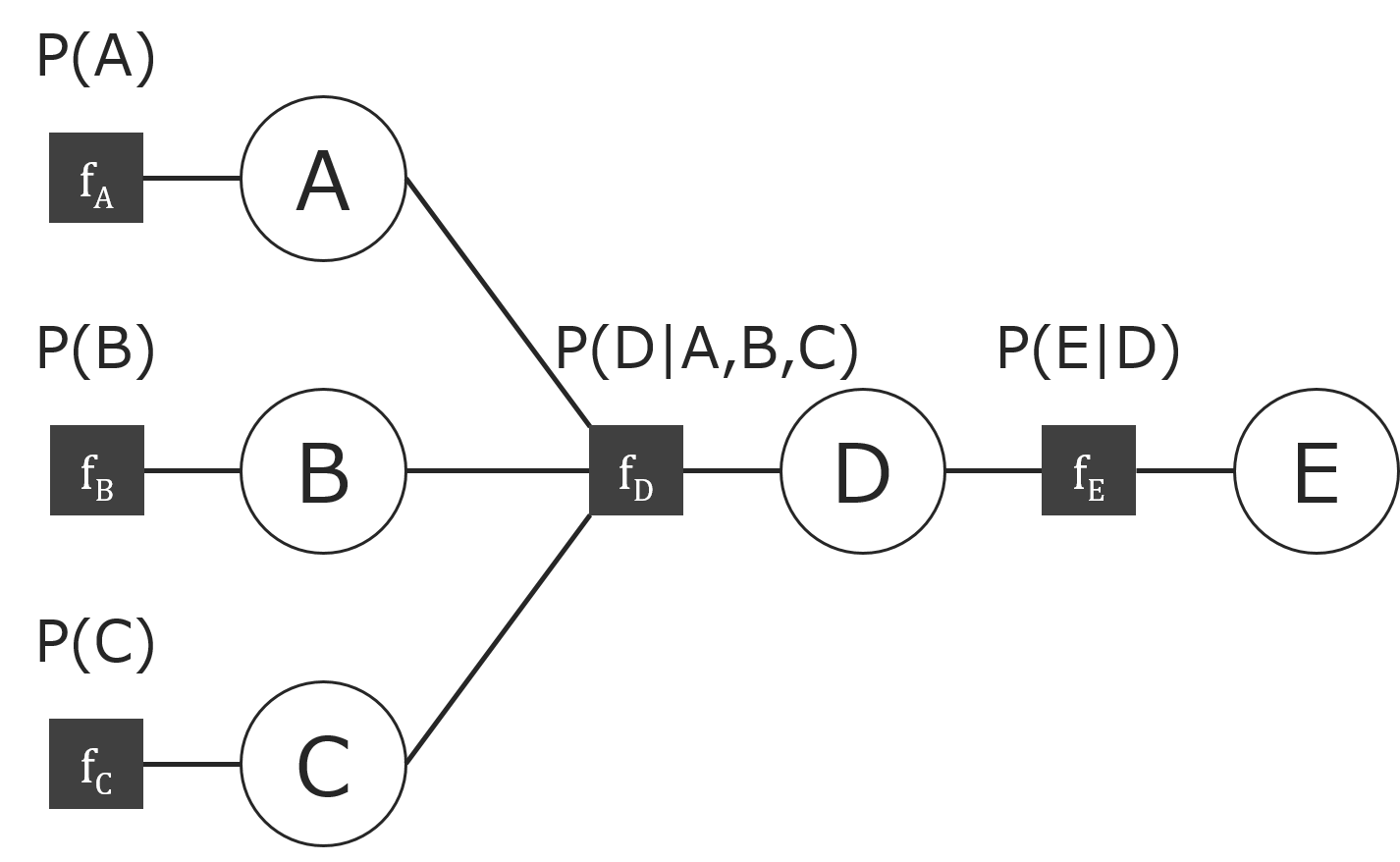
今度は、$C$と$E$が観測されてるとして、$A$を周辺化することを考えます。
同様に、まず素直に計算すると、上図より$P(A,B,C,D,E)=P(A)P(B)P(C)P(D|A,B,C)P(E|D)$で、
\begin{align}
P(A,C=c,E=e) &= \sum_{B}\sum_{D}P(A,B,C=c,D,E=e) \\
&= \sum_{B}\sum_{D} P(A)P(B)P(C=c)P(D|A,B,C=c)P(E=e|D) \\
&= P(A)P(C=c)\sum_{B}P(B)\sum_{D}P(D|A,B,C=c)P(E=e|D)
\end{align}
例1で既に分かっている計算については省略します。今回、3つ以上の変数ノードが接続した関数ノードから変数ノードへのメッセージの計算を知りたいので、$m_{f_D \rightarrow A}$に着目します。
$P(A,C=c,E=e)= m_{f_A \rightarrow A} m_{f_D \rightarrow A}$で、$m_{f_A \rightarrow A} = P(A)$なので、上の結果より、
$m_{f_D \rightarrow A} = P(C=c)\sum_{B}P(B)\sum_{D}P(D|A,B,C=c)P(E=e|D) $
であると分かります。
$m_{B \rightarrow f_D} = P(B)$
$m_{C \rightarrow f_D} = P(C=c)$
$m_{D \rightarrow f_D} = P(E=e|D)$
より、$m_{f_D \rightarrow A}$は、
$m_{f_D \rightarrow A} = m_{C \rightarrow f_D} \sum_{B} m_{B \rightarrow f_D} \sum_{D} m_{D \rightarrow f_D} P(D|A,B,C=c) $
となり、一般に、
$m_{f \rightarrow v} = \sum_{v_1}m_{v_1 \rightarrow f} \sum_{v_2}m_{v_2 \rightarrow f} \cdots \sum_{v_n}m_{v_n \rightarrow f} f(v, v_1,v_2, \cdots ,v_n)$
あるいは、表記の簡単のため、全てのメッセージを最も内側の$\sum$に入れて、
$m_{f \rightarrow v} = \sum_{v' \in n(f)\backslash v} f(\mathbf{v}) \prod_{v' \in n(f)\backslash v} m_{v' \rightarrow f} $
と書かれる事が最も一般的です。ここで、$v_1,v_2, \cdots ,v_n$は$n(f) \backslash v$に等しく、$v$以外の$f$に隣接した変数ノードです。また、観測されている(固定されている)変数については、その変数が取りうる値の集合を観測された変数だけを含む集合としてみなしてやれば、上記の総和の表記に含めて問題ないことが分かります。
例1で、関数ノードから変数ノードへのメッセージを求める際に、
従って、関数ノード$f$から変数ノード$v$へのメッセージ$m_{f\rightarrow v}$は、$f$に直接接続する$v$を除く全ての変数に関して総和を取ることが分かります。
と説明しましたが、変数ノードが複数ある時もメッセージは確かにそうなっていることが分かりました。
以上までの議論より、完全なBPアルゴリズムの式は以下の様になります。
$v$を変数ノード、$f$を関数ノード、$n(v), n(f)$をそれぞれ、隣接したノードの集合とした時、
\begin{align}
P(v) \hspace{5pt} &= \hspace{7pt} \prod_{f \in n(v)} \hspace{4pt} m_{f \rightarrow v} \\[5pt]
m_{f \rightarrow v} \hspace{5pt} &= \hspace{2pt} \sum_{v' \in n(f)\backslash v} f(\mathbf{v}) \hspace{2pt} \prod_{v' \in n(f)\backslash v} m_{v' \rightarrow f} \\[5pt]
m_{v \rightarrow f} \hspace{5pt} &= \hspace{2pt} \prod_{f' \in n(v)\backslash f} m_{f'\rightarrow v}
\end{align}
BPアルゴリズムに関する今までの議論は、全て比較的簡単な具体的なグラフを用いてのやや直感的な説明でしたが、一般のグラフ(木)について考えても、全く同様の議論で、このメッセージパッシングによって周辺確率が求まることが証明できます(が、証明についてはここではこれ以上は踏み込みません)。
BPアルゴリズムは、別名sum-productアルゴリズムとも呼ばれますが、名前の通り(関数ノードと変数ノードとで)和と積を繰り返し計算するアルゴリズムとなっていることが分かります。
例3
BPアルゴリズムは本当に大切なアルゴリズムですので、理解を深めるために最後にもう一度、少し複雑なグラフで計算をしてこの章を終えたいと思います。
ファクターグラフのセクションで2つめに取り上げたグラフを再掲します。(同様に、分かりやすさのために関数ノードに名前を付けています。)

ここでは、$E$が観測されてるとして、$B$を周辺化することを考えます。
また、今回は、最初からBPアルゴリズムを用いて計算します。
BPアルゴリズムを用いて、メッセージをどんどん計算していきましょう。
$m_{C \rightarrow f_E} = m_{f_C \rightarrow C} = P(C)$、$m_{F \rightarrow f_F} = 1$なので、
$m_{f_E \rightarrow D} = \sum_{C} m_{C \rightarrow f_E} P(E=e|C,D) = \sum_{C} P(C)P(E=e|C,D) $
$m_{f_F \rightarrow D} = \sum_{F} P(F|D) = 1 $
より、
$m_{D \rightarrow f_D} = m_{f_E \rightarrow D} \hspace{2pt} m_{f_F \rightarrow D} = \sum_{C} P(C)P(E=e|C,D)$
また、$m_{A \rightarrow f_D} = m_{f_A \rightarrow A} = P(A)$なので、
$m_{f_D \rightarrow B} = \sum_{A} m_{A \rightarrow f_D} \sum_{D} m_{D \rightarrow f_D} P(D|A,B) = \sum_{A}P(A)\sum_{D} \bigl( \sum_{C} P(C)P(E=e|C,D) \bigr) P(D|A,B) $
$m_{f_B \rightarrow B} = P(B)$なので、
$P(B,E=e)=m_{f_B \rightarrow B}\hspace{2pt}m_{f_D \rightarrow B} = P(B) \sum_{A}P(A)\sum_{D} \bigl( \sum_{C} P(C)P(E=e|C,D) \bigr) P(D|A,B) $
のように、求まりました。
TrueSkill
さて、いよいよ本題のTrueSkillについてお話します。
ここまで読んだ方ならお気づきかも知れませんが、TrueSkillは各プレイヤーのskill(=強さ、レーティング)を確率変数としたグラフィカルモデルを考え、その上で推論することで、各プレイヤーのskillの事後周辺確率を導出します。
TrueSkillではすぐ分かるようにほとんどの確率変数にガウス分布を仮定しています。
これは、ガウス分布が標準的な確率分布であるという以上に、後で見るようにガウス分布同士の様々な組み合わせの計算の結果がまたガウス分布になるという性質を持っているため、事後確率の計算が解析的に容易に計算可能であるからです。
注:実際、全ての確率変数がガウス分布とその線形和(ガウス分布の線形和は、またガウス分布の形(ガウシアン)になる)で構成されるグラフィカルモデルを特に線形ガウシアンモデルと呼び、物体追跡やロボット制御の分野などでよく使われています。
ただ、一点のみ事後確率がガウス分布の形で 表されない点があり、その点だけガウス分布で近似するということを考える必要があります。
以降では、まず、ガウス分布を簡単に紹介し、TrueSkillが想定するモデルを説明し、それをグラフィカルモデル(ファクターグラフ)の形で表現します。その後、そのファクターグラフ上での推論のためにBPアルゴリズムを適用することを考え、具体的な個々のメッセージの計算を確認し、ガウス分布の形にならないメッセージについて、どう近似計算すればいいかを示します。
ガウス分布
ガウス分布は正規分布とも呼ばれ、最もよく使われる標準的な確率分布でしょう。
参考:特に、中心極限定理により、ランダムな観測ノイズを含む様々な観測変数についてガウス分布を仮定することが正当化されます。
ガウス分布は以下の形で表されます。
$p(x)=N(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\bigl(-\frac{(x-\mu)^2}{2\sigma^2}\bigr)$
ここで、特に$\mu$, $\sigma^2$は、それぞれ当該分布の平均と分散になり、ガウス分布はこの2つのパラメータによって決定づけられます。
参考:このように、確率分布内にパラメータを持ち、あるパラメータの値によって具体的な一つの確率分布に決定されるような確率分布をパラメトリックな確率分布と呼び、機械学習ではしばしば用いられます。
今後ガウス分布は、特に断りなく、$N(x|\mu,\sigma^2)$の形式で表現します。
また、正規化項$\frac{1}{\sqrt{2\pi\sigma^2}}$を除いた、ガウス分布に比例した関数を一般にガウシアンと呼びます。逆に、ガウシアンを確率密度関数として成り立つよう$\int p(x) dx = 1$となるよう正規化項を掛けたものはガウス分布になります。
TrueSkillのグラフィカルモデル
まず、TrueSkillが考えるモデルを言葉で簡単に説明します。
TrueSkillでは各プレイヤーのskill(=強さ、レーティング)をガウス分布に従う確率変数であるとし、各試合におけるプレイヤーの実際のperformance(=パフォーマンス)はプレイヤーのskillを中心としたガウス分布に従うとします。また、team(=チーム)の強さは構成するプレイヤーのperformanceの和によって求まるとし、最終的な勝ち負けはteam間の強さのdifference(=差)によって決定されるとします。具体的にはdifferenceが$\epsilon$より大きければ勝ち、$-\epsilon$より小さければ負け、その間の数値であれば引き分けとします。
まとめると、TrueSkillには以下の確率変数が現れ、
$s_i$:各プレイヤーのskill
$p_i$:各プレイヤーのその試合における実際のperformance
$t_i$:各チームのその試合における強さ。チームに所属するプレイヤーのパフォーマンスの和によって求まる
$d_i$:その試合で対戦した各チーム間の強さの差
各確率変数は以下の関係を持ちます。
$s_i$:$N(s_i|\mu_i,\sigma_i^2)$
$p_i$:$N(p_i|s_i,\beta^2)$
$t_i$:$\sum_{j \in t_i} p_j$
$d_i$:$t_j - t_k$
参考:各プレイヤーのスキルは時間経過によって変化すると考えるのが自然と思うかもしれません。その場合、例えば$p(s_{i,t+1}|s_{i,t})=N(s_{i,t+1}|s_{i,t},\gamma^2)$のような遷移確率を導入することで変化を表すことができます(この場合、$T=t+1$時の$s_i$に$\gamma^2$分追加の分散が乗る形になるだけでアルゴリズムはほとんど変えなくて良い)。このような拡張性や自由度の高さもグラフィカルモデルで表現することの魅力です。
今、プレイヤーが1~4の4人いて、プレイヤー1 v.s. プレイヤー2とプレイヤー3のチーム v.s. プレイヤー4の計3チームが対戦し、プレイヤー1が1位で、それ以外の2チームが同率2位であった場合の、各確率変数の関係をファクターグラフで表現すると以下の様になります。なお、図中のⅡは、各確率変数が式の関係を満たすことを示しています。

TrueSkillにおけるBPアルゴリズム
TrueSkillが考えるモデルをファクターグラフで表現できたので、後はこのグラフ上での推論のためにBPアルゴリズムを適用することを考えます。
これ以降の議論は、簡単のためにチームはない(つまりプレイヤー同士が組むことはない)ものとします。(アルゴリズム的な見地では、チームの有る無しによる本質的な差異はほとんど無く、説明の上でただ冗長さが増すだけだからです。)
チームを除いた場合の、ファクターグラフは以下の様になります。
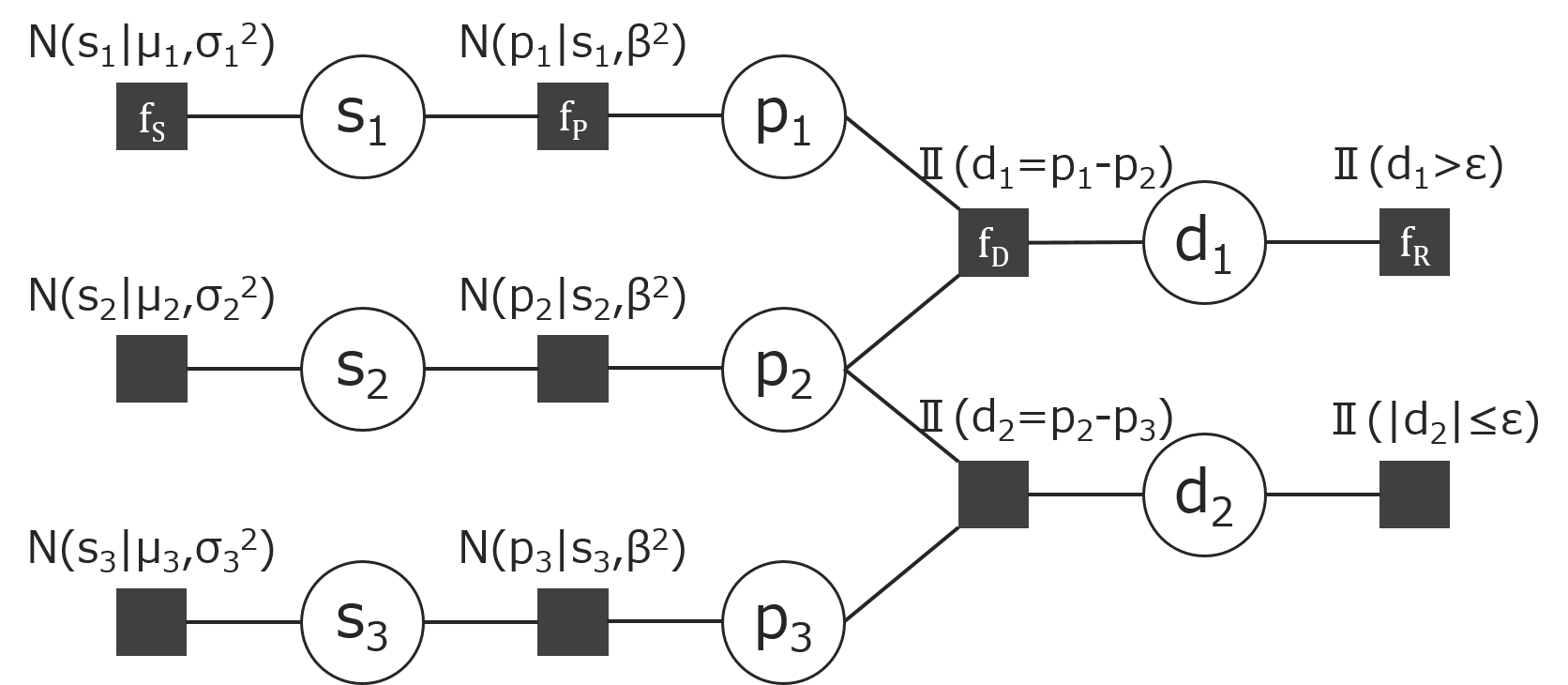
このファクターグラフ上に存在する、自明な計算であるものを除いた、相異なるメッセージの計算は以下の6つになります。(自明な計算とは例えば、$m_{s_i \rightarrow f_P} = m_{f_S \rightarrow s_i}$などBPアルゴリズムから直ちに求まるものをここでは指します。変数ノードでの計算がそれに当たります。)
- $m_{f_S \rightarrow s_i}$
- $m_{f_P \rightarrow p_i}$
- $m_{f_D \rightarrow d_i}$
- $m_{f_R \rightarrow d_i}$
- $m_{f_D \rightarrow p_i}$
- $m_{f_P \rightarrow s_i}$
これらのメッセージ1からメッセージ6を以下で、実際に計算していきますが、まず初めに簡単にアウトラインを説明します。
各メッセージは単に数学的に数式上で表現できるだけでなく、最終的にプログラムで実際に現実的に計算可能であることが求められます。
以降で計算すると分かるように、ガウス分布の和も積もまたガウス分布の形(ガウシアン)になるため、グラフ上のほとんどのメッセージは自然にガウシアンで表現できます。
ただ一点、メッセージ4だけ、ガウシアンにならないため、これをうまくガウシアンで近似してやることで、グラフ上をわたる全てのメッセージがガウシアンとなり、これはプログラムで表現、計算可能です。
特に、最終的に求めたいものは、プレイヤーのskillである、周辺確率$p(s_i)$ですが、これもガウシアンの積になりますが、$p(s_i)$は必ず確率分布になっているため、ガウシアンの、ガウス分布で言う所の平均($\mu$)と分散($\sigma^2$)のパラメータだけ保持していれば、正規化項を$\frac{1}{\sqrt{2\pi \sigma^2}}$で計算できるため十分なことが分かります(途中の計算で正規化項(定数倍)の部分については完全に省略できる)。従って、これ以降では$N(x|\mu,\sigma^2)$という表現であっても特に正規化項の正誤については考えません。
さて、以前のセクションで求めた、BPアルゴリズムを読者の便のために再掲します。ここでは、確率変数は連続変数であるため、総和が積分にのみ変わっています。
\begin{align}
P(v) \hspace{5pt} &= \hspace{7pt} \prod_{f \in n(v)} m_{f \rightarrow v} \\[5pt]
m_{f \rightarrow v} \hspace{5pt} &= \hspace{7pt} \int \cdots \int \hspace{1pt} f(\mathbf{v}) \hspace{-2pt} \prod_{v' \in n(f)\backslash v} \hspace{-5pt} m_{v' \rightarrow f} \hspace{4pt} d \mathbf{v}_{\backslash v} \\[5pt]
m_{v \rightarrow f} \hspace{5pt} &= \hspace{2pt} \prod_{f' \in n(v)\backslash f} \hspace{-5pt} m_{f'\rightarrow v}
\end{align}
メッセージ4の計算は複雑なため、最後に回しています。
メッセージ1

$m_{f_S \rightarrow s_i}$は、BPアルゴリズムの説明でも話した通り、単に$N(s_i|\mu_i,\sigma_i^2)$になります。
メッセージ2
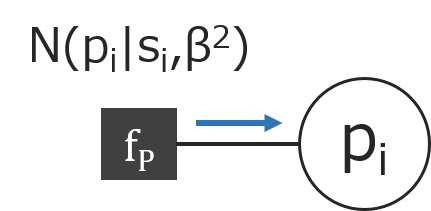
$m_{f_P \rightarrow p_i}$は、$m_{s_i \rightarrow f_P} = N(s_i|\mu_i, \sigma_i^2)$とすると、BPアルゴリズムより、
\begin{align}
m_{f_P \rightarrow p_i} &= \int N(p_i|s_i,\beta^2) m_{s_i \rightarrow f_P} ds_i \\
&= \int N(p_i|s_i,\beta^2) N(s_i|\mu_i, \sigma_i^2) ds_i \\
&= N(p_i|\mu_i, \beta^2 + \sigma_i^2)
\end{align}
なので、$m_{f_P \rightarrow p_i} = N(p_i|\mu_i, \beta^2 + \sigma_i^2) $となります。
メッセージ3
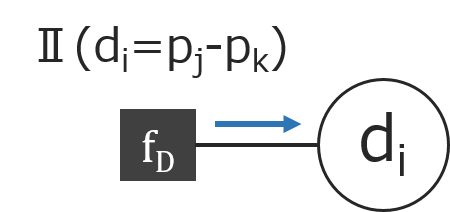
$m_{f_D \rightarrow d_i}$は、$m_{p_j \rightarrow f_D} = N(p_j|\mu_j, \sigma_j^2), m_{p_k \rightarrow f_D} = N(p_k|\mu_k, \sigma_k^2)$とすると、$d_i=p_j-p_k$で、独立した正規分布に基づく確率変数の線形和は、また正規分布になるので(この性質を特に再生性と言います)、確率の基本定理より、
$E[X-Y] = E[X] - E[Y]$
$V[X-Y] = V[X] + V[Y]$
が成り立つので、$m_{f_D \rightarrow d_i} = N(d_i|\mu_j - \mu_k, \sigma_j^2 + \sigma_k^2) $となります。
メッセージ5

$m_{f_D \rightarrow p_j}$と$m_{f_D \rightarrow p_k}$は、$p_j=d_i+p_k$、$p_k=-d_i+p_j$で、
$m_{d_i \rightarrow f_D} = N(d_i|\mu_i, \sigma_i^2), m_{p_j \rightarrow f_D} = N(p_j|\mu_j, \sigma_j^2), m_{p_k \rightarrow f_D} = N(p_k|\mu_k, \sigma_k^2)$とすると、
メッセージ3と同様、確率の基本定理より、
$E[X+Y] = E[X] + E[Y]$
$V[X+Y] = V[X] + V[Y]$
が成り立つので、$m_{f_D \rightarrow p_j} = N(d_i|\mu_i + \mu_k, \sigma_i^2 + \sigma_k^2)$、$m_{f_D \rightarrow p_k} = N(d_i| -\mu_i + \mu_j, \sigma_i^2 + \sigma_j^2)$となります。
メッセージ6
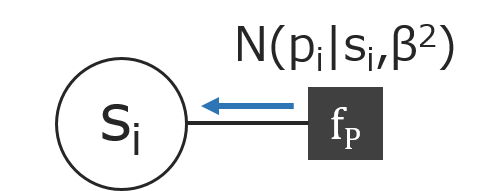
$N(p_i|s_i,\beta^2)=\frac{1}{\sqrt{2\pi\beta^2}}\exp\bigl(-\frac{(p_i-s_i)^2}{2\beta^2}\bigr)=\frac{1}{\sqrt{2\pi\beta^2}}\exp\bigl(-\frac{(s_i-p_i)^2}{2\beta^2}\bigr)=N(s_i|p_i,\beta^2)$より、
$m_{p_i \rightarrow f_P}=N(p_i|\mu_i, \sigma_i^2)$とすると、
$m_{f_P \rightarrow s_i} = \int N(s_i|p_i,\beta^2) N(p_i|\mu_i, \sigma_i^2) dp_i$となり、メッセージ2で計算したように、
$m_{f_P \rightarrow s_i} = N(s_i|\mu_i, \beta^2 + \sigma_i^2) $となります。
メッセージ4

メッセージ4はTrueSkillで最も計算が複雑なメッセージで、厳密解はもはや解析的でないため、近似することを考えます。
メッセージ4の計算は、勝ち、負け、引き分けでそれぞれ計算が異なりますが、まず上のグラフのように勝った場合を考えます。
メッセージ4の計算は後ほど追記します。
まとめ
これで、BPアルゴリズムで必要な、TrueSkillのファクターグラフ上の全てのメッセージを計算できることが分かりました。
一点だけ、グラフにループのある場合や、今回のようにメッセージに近似計算が含まれている場合は、普通のBPアルゴリズムと違い、より厳密解に近い解を得るために収束するまでメッセージパッシングを続ける必要があります。
実装
ここまで説明してきた、TrueSkillをRubyで実装してみようと思います。分かりやすい様に、必要な各要素をstep by stepで実装していきます。
注:但し、あくまでTrueSkillへの理解を深めるための実装であって、実務での運用のための実装ではないため、汎用性やパフォーマンスよりは分かりやすさを重視した実装となっている点ご注意下さい。
また、ここでも簡単のためにチームは考えないものとします。
もう実装はしてあるのですぐ後で追記しますm(_ _)m
実験
折角実装したので思考上の簡単な例での実験を後で追記する予定ですm(_ _)m
最後に
ここまでお読みいただきありがとうございます。
機械学習入門の方は、どうして入門書の多くは最初にことさら情報理論や確率分布について詳しく説明してあるのかなんとなく掴めたのではないかと思います。結局、それらの理論が実際の多くの機械学習アルゴリズムでふんだんに活用されているからです。
こうした具体的な問題を解決する具体的なアルゴリズムを知り、学ぶことで、それらのベースとなる知識・理論も勉強する意欲も起きるのではないでしょうか。そうなれば幸いです。
明日(今日)は僕の友人であり、現在は同僚でもある@ororogによる「ガウス過程による回帰」です。
乞うご期待!