はじめに
この記事は基本概念から項目特性曲線(2PLM)の実装までをまとめた内容です。項目反応理論はあまり内容が深いので、今回はイメージできたら幸いです。違っている点などがあればご指摘お願いします。基本概念
Wikipediaによると、評価項目群への応答に基づいて、被験者の特性(認識能力、物理的能力、技術、知識、態度、人格特徴等)や、評価項目の難易度・識別力を測定するための試験理論である。簡単に言うと、項目(問題)に対する受験者の回答(正誤)のデータを見ることで、その設問の難易度が高いのか低いのか、また能力の高い、低いを適切に識別できる問題かどうかが分かり、それにより受験者の能力も正しく評価できる、という考え方である。
IRTを使用している主なテスト
| カテゴリー | 例 |
|---|---|
| 民間英語試験 | TOEIC・TOEFL・GTEC・CASEC |
| 学力調査試験 | PISA・TIMSS・NAEP |
| 心理尺度の作成・評価 | 性格判定、購買力尺度、進取的行動尺度 |
項目反応理論の基本(良いところ)
テストを運用する際がよく直面する問題は、例えば、ある学校の今年度試験の平均点が昨年の平均点より伸びたため、その学校の生徒たちの学力が平均的に高くなったと考えられるか?実はそうではなく、今年度のテストが簡単になっただけかもしれないし、仮に難易度が同じあったとしても、受験を受けた学生たちの集団も異なった可能性がありえる。このような問題は、該当のテスト項目や受験者集団の性質に依存したものとなる。
そこで、IRTでは、テスト・尺度を受けた集団や問題(項目)に直接的に依存しない評価が可能。
それを実現するために、項目反応モデルと呼ばれる数理モデルと、等化と呼ばれる手続きである。
項目反応モデル
項目反応モデルとは、個人の能力・適性・態度等の直接観測できない潜在特性値をモデルに組み込み、ある**潜在特性値θ**を示す個人がある項目(問題)に正答する確率を表現。| よくある項目反応モデル | |
|---|---|
| 1 | ロジスティック・モデル(logistic model) |
| 2 | 正規累積モデル(normal ogive model) |
| 3 | ラッシュモデル(Rasch model) |
| 4 | 段階反応モデル(graded response model) |
| 5 | 部分的反応モデル(partial credit model) |
| 6 | 名義反応モデル(nominal response model) |
| 7 | 連続的反応モデル(continuous response model) |
| 8 | 拡張ロジスティックモデル(generalized logistic model) |
| 9 | 一般正規累積モデル(general normal-ogive model) |
色々モデルがあるが、一般的には、ロジスティクス・モデル(項目特性曲線)が使われる。
ロジスティクス・モデルで扱うパラメータ:
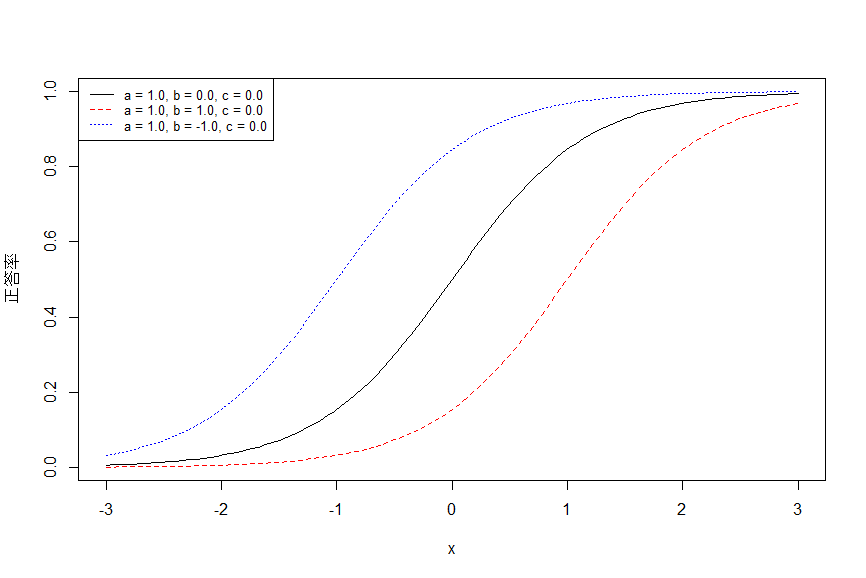
1.識別力(a):受験者の特性値(能力)の違いが正答率にどの程度反映するか。
2.困難度(b):大きいほどテスト項目が難しい問題である。
3.当て推量(c):受験者が偶然正答する確率。
項目特性曲線(Item Characteristic Curve:ICC)
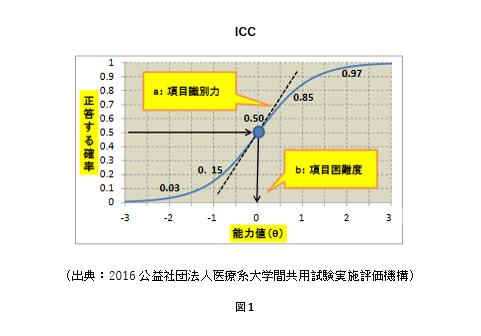
項目特性曲線 (item characteristic curve:ICC)とは、項目反応理論において各項目ごとに推定される曲線である。x軸は測定する特性値、y軸にはその特性を持っている場合に各項目が正答となる確率(正答率)となる。
ICCは、困難度(正当となるにはどのくらい高い特性値が必要か)と識別力(項目はどの程度の特性値を識別することに長けているか)という2つのパラメータを持つ。
図1が示すグラフは、項目の識別力(a)と困難度(b)によってテスト項目の正答確率を表現しようとするモデル。横軸は受験者の能力値(θ)、縦軸は該当項目の正答率となる。横軸の能力値(θ)が増加するにつれて、縦軸の正答確率が向上することを表現している。識別力(a)と困難度(b)の分離することによって、テスト項目や受験者集団に依存する問題を克服することができる。
項目特性曲線(2PLM)の実装
2PLMの場合は、
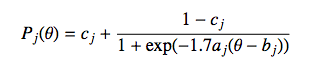 (1)
(1)
a=識別度、b=困難度、c=0、D=1.7(定数)、j=項目番号、θ=受験者能力、exp=指数関数で求めることができる。
実装
データはここからダウンロードして、"testeg.csv"を読み込む。#データの読み込み
data <-read.csv("testeg.csv")
#項目反応パン行列
dim(data)
#20 11
#正答者数n_j
apply(data[,2:11],2,sum)
# q1 q2 q3 q4 q5 q6 q7 q8 q9 q10
# 13 17 13 12 18 16 15 8 4 15
#項目特性値
library(ltm)
descript(data[,2:11])
これによって、困難度(b)と識別力(a)を求めることができた。
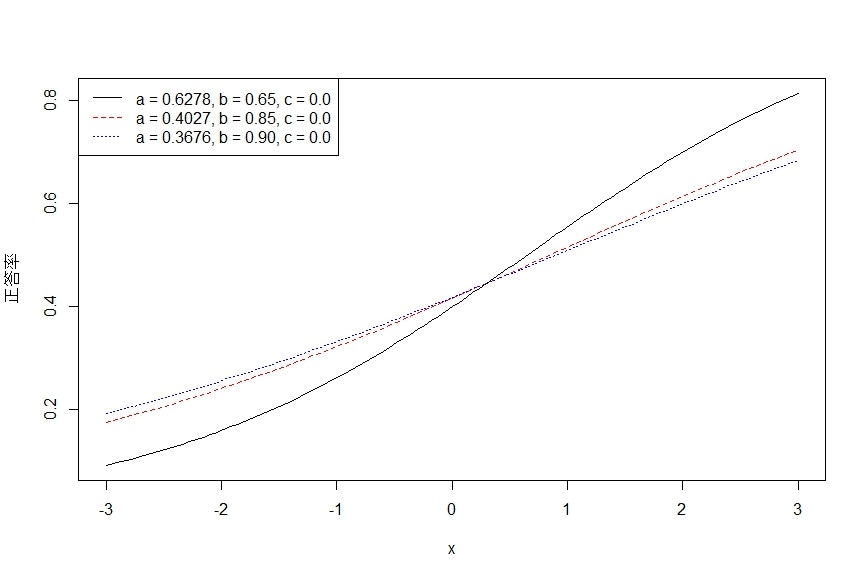
求めたい項目特性曲線の困難度(b)と識別力(a)を方程式(1)に代入し、項目特性曲線(2PLM)を生成しましょう。以下はコードです(c=0、D=1.7(定数)。
#項目1
# a = 0.6278, b = 0.65 , c = 0.0
curve((1 + 0)/(1 + exp(-1.7*0.6278*(x-0.65))), -3, 3, col = "black", lty = 1, ylab = "正答率")
#項目2
# a = 0.4027, b = 0.85, c = 0.0
curve((1 + 0)/(1 + exp(-1.7*0.4027*(x-0.85))), -3, 3, col = "red", lty = 2, add = TRUE)
#項目5
# a = 0.3676, b = 0.90, c = 0.0
curve((1 + 0)/(1 + exp(-1.7*0.3676*(x-0.90))), -3, 3, col = "blue", lty = 3, add = TRUE)
#凡例を生成
legend("topleft",
legend = c("Q1:a = 0.6278, b = 0.65, c = 0.0", "Q2:a = 0.4027, b = 0.85, c = 0.0", "Q5:a = 0.3676, b = 0.90, c = 0.0"),
col = c("black", "red", "blue"),
lty = 1:4, cex = 1.0)
上記のコードを実装すれば、下記のような項目特性曲線(2PLM)が生成された。
解説
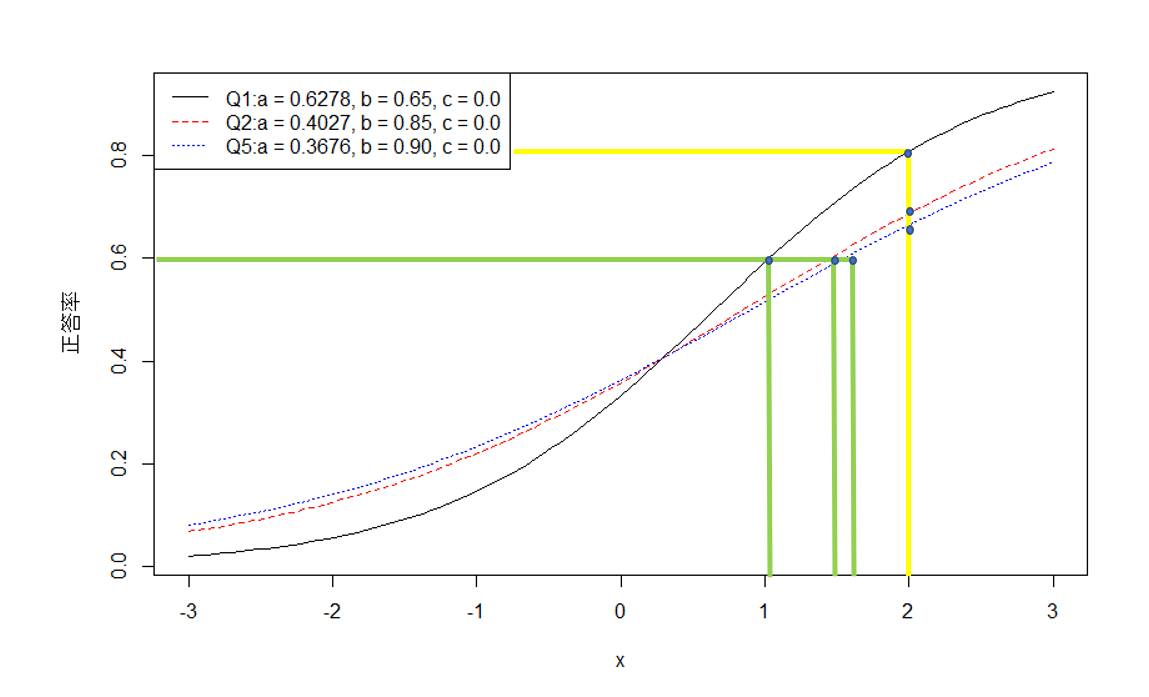
グラフからわかったのは、1、横軸は受験者の能力値(x)、縦軸は該当項目の正答率となり、横軸の能力値(x)が増加するにつれて、縦軸の正答確率が向上することを表現している。
2、同じ能力を持つ受験者において、項目の難易度順がQ5>Q2>Q1となる。
3、仮に同じ回答率60%を達成する場合、項目Q1に応じる能力が1.1、項目Q2に応じる能力が1.5、項目Q5に応じる能力が1.7である。
さいごに
いかがでしょうか。 Rで実装するのはシンプルだが、理論を理解するのは時間がかかる。今回はほんの一部を書いてみたが、余裕があったら、記事編集して充実させたいと思う。参考文献
(1)項目反応理論とは:https://ja.wikipedia.org/wiki/項目応答理論
(2)項目特性曲線 (item characteristic curve:ICC)とは:https://clover.fcg.world/2016/06/28/5621/
(3)加藤健太郎,川端一光,山田剛史(2014年)「Rによる項目反応理論」 株式会社 オーム社