はじめに
過去に何度書いていますが、今回もIBM Quantum Challengeで最後の問題について解説記事を書いてみたいと思います。今回は順位が付くような問題は無かったのですが、最後の問題がチャレンジグでそれの量子回路を如何に改良するかが面白かったのと、おそらく全参加者でも2位ぐらいに短く効率的な回路を書くことに成功したんですが、どこにもそういった記事や解説が存在しなかったので、せっかくということでその詳細を紹介したいと思います。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
IBM Quantum Challenge Spring 2023とは
IBM Quantum Challengeをご存じない方に軽く概要を紹介します。ご存じの方は読み飛ばしてください。
これはIBM Researchが毎年春と秋の2回開催している、量子プログラミングコンテストです。2018年から開催しており、世界中の腕自慢から、初心者の方まで約1500人規模で参加者が同じ期間で一斉にプログラミングをして腕を磨きます。
内容は入門的な内容から始まって、最後はエキスパートでも骨が折れる問題が出てきて、どのレベルでも楽しめるようになっています。特に最近は直前に新規実装された目玉の機能などを使い倒せるようになってもらうように教育的配慮で問題が組まれているので、初心者でも安心して参加して、一定のレベルまで到達できます。クリアするとデジタルバッジが発行されるので、参加したエビデンスを得ることもできます。
今回は、今年の春の大会についてです。テーマは「動的回路(Dynamic Circuit)」と呼ばれるもので、途中で一部の量子ビットに対して測定を行い、その測定結果を元に他の量子ビットに操作を行うような機能が追加されました。if文のようなものと考えていただけるとイメージしやすいと思います。
また、今回の目玉は最後の問題で127量子ビットの実機を使って計算をさせることができるということで、専門家の間ではざわつくようなことがありました。この記事はその時の問題と、実際に効率的に動かすために量子回路を限界まで縮めることに挑戦した記録になります。
具体的にはこちらのJupyter Notebookで出題されています。
127量子ビットデバイス
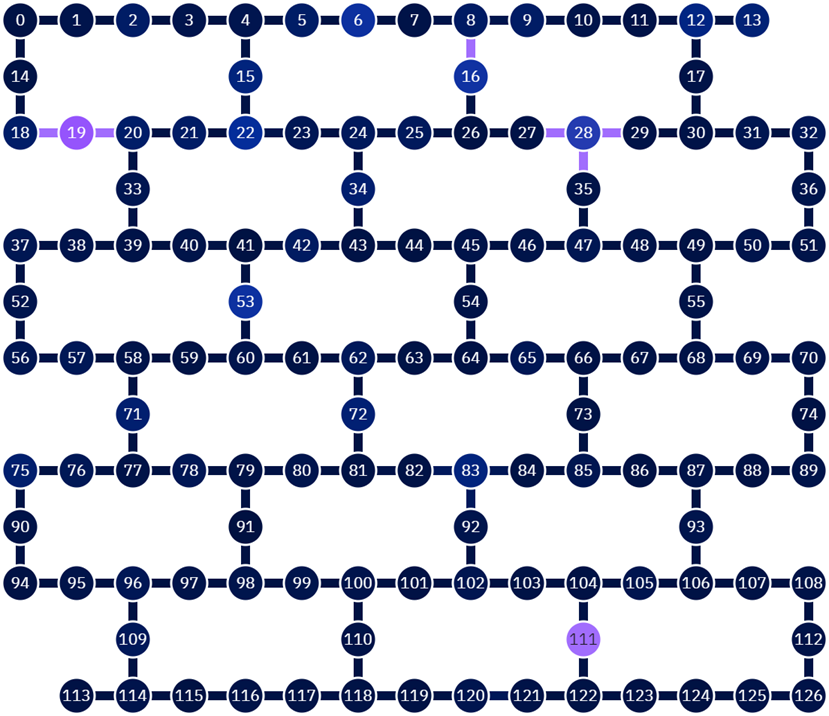
今回使える127量子ビットデバイスは、こんな感じなっています。見方としては、各番号が個々の量子ビットに対応しており、それらを繋ぐ線はお互いの量子ビットを使って直接処理が行うことが可能かどうかを示しています。専門的な言葉で言えば、CNOTの処理を直接繋げられるかどうか、ということを表しています。また、色が微妙に違う量子ビットがありますが、これはエラー率の違いを表しています。量子ビットもそれぞれに個性があるということを表しています。なんだかニンゲンみたいですねw
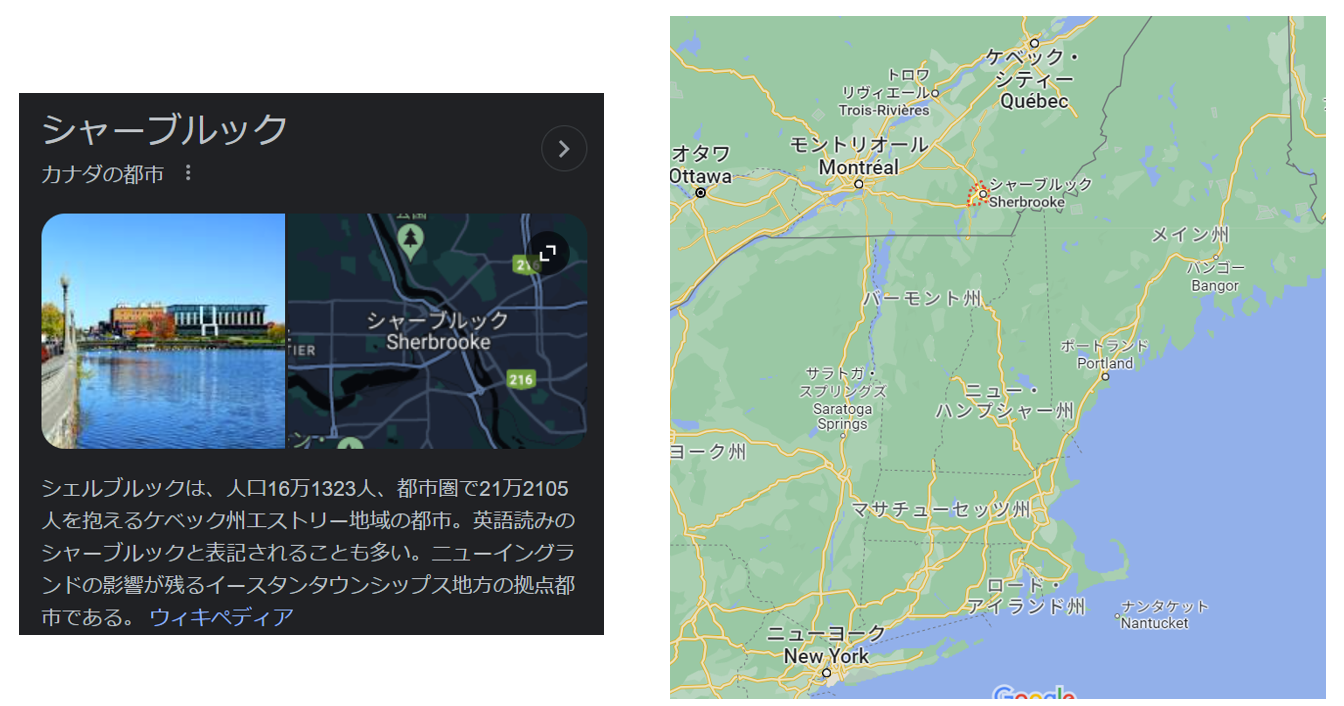
余談ですが、このデバイスの名前ですが、ibm_sherbrookeと呼ばれています。
Sherbrookeとはカナダ西部の都市の名前です。IBMの量子デバイスは他にも有名な都市の名前を付けられています。(TokyoとかManilaとか)実際にその都市に置いてあるわけではないはずなので、あくまで名称だけとお考え下さい。
今回はこのデバイスが一般に初披露されることもあり、しかもしれを使えるということで、それに合わせて問題が作られています。ここからはそれを解説していきます。
問題を解く(Lab5)
簡単に要約すると、この127量子ビットの実機に指定された量子状態を生成し、それで動かしてみてね、という話です。基本的には誘導に乗って行けばクリアできます。
ここではGHZ状態というキーワードが出ているので、先にそれを説明しておきます。
GHZ状態とは
GHZ状態とは、すごく雑に説明すると、すべての量子ビットの測定結果が$\ket{0}$もしくは$\ket{1}$になり、それが半々の確率で測定される状態を指します。もう少し詳しく言うと、どれか1つの量子ビットを測定したときに出てきた結果が、他の量子ビットでも同じように出る状態となっています。全ての量子ビットが同期している状態になっているようなものと考えることができます。
数学的には以下のように表記します。$n$は量子ビット数です。
\frac{\ket{0000\cdots0} + \ket{1111\cdots1}}{\sqrt{2}} = \frac{\ket{0}^{\bigotimes n} + \ket{1}^{\bigotimes n}}{\sqrt{2}}
一般的には$n\geq3$の場合をGHZ状態と呼びます。$n=2$の場合はよく知られたEPR状態と呼ばれるもので、$\frac{\ket{00} + \ket{11}}{\sqrt{2}}$となっています。$n=1$の場合は$\frac{\ket{0} + \ket{1}}{\sqrt{2}}$であり、最も基本的な重ね合わせ状態を示しています。広義の意味では$n=1,2$の場合もGHZ状態の一種とみなすことができると言えます。(基本的にはそう呼ばないですが)
さて今回はこれを実装してみるというのが、出題されています。では、実際に問題を見ていきましょう。
Exercise1(全量子ビットをGHZ状態にする)
やって欲しいことは全量子ビットをエンタングルさせて、127量子ビットのGHZ状態を作ってください、というものです。上記で言えば、$n=127$に相当します。
いきなり、127から考えるのは難しく感じるので、$n=2$と$n=3$のケースで考えてみましょう。
$n=2$は次の通りです。いずれか1つの量子ビットにHadamardゲートをかけて重ね合わせ状態を作り、その状態を制御ビットにして残りの量子ビットをターゲットにすることで量子もつれ(エンタングル)状態を作ることができます。
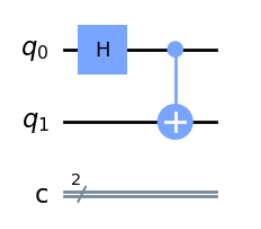
$n=3$の場合も考え方は同じで、重ね合わせになっている量子ビットを制御にして、残りに一個ずつCNOTをかけることで簡単に作成することができます。
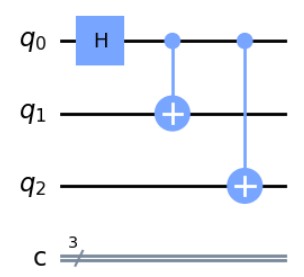
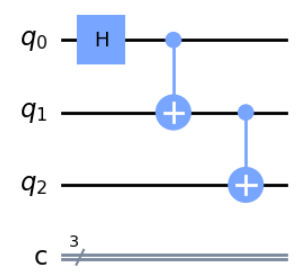
実はこう書いても同じ状態を実現することができます。要は一度でもGHZ状態になった量子ビットであればどれでも良いので、そのどれかを制御ビットにして、まだ真っ新な量子ビットをターゲットにすることで量子もつれの仲間にすることができます。次々にゾンビにかまれて増殖していくようなイメージでしょうか。
この考え方は、後で回路を短くするときに使います。
数学的にどうなっているなどは、こちらの記事に具体的に書いてあるので、ぜひ参考にしてみてください。
さて、では$n=127$のケースですが、この方法で作ることができます。まずは最もコードとしては簡単な方法を紹介します。
qc = QuantumCircuit(127,127)
qc.h(0)
for n in range(1,127):
qc.cx(0,n)
このコードを書けば、問題はパスすることができます。ただし、これは実機には優しくなくて、実際にこのコードで動かそうとすると、回路が長くなりすぎて、動かすのに時間がかかるし、ノイズが乗りまくって、使い物にならない結果になってしまいます。この後で回路を短くする改良を紹介します。
Exercise2(一部の量子ビットをアンエンタングルさせる)
はい、、、何言っているのかいまいちわかりませんね。実は自分も最初見たときは意味がわかりませんでした。ただし、図にするとわかりやすくなります。
以下のような状態を生成して欲しいという内容になります。
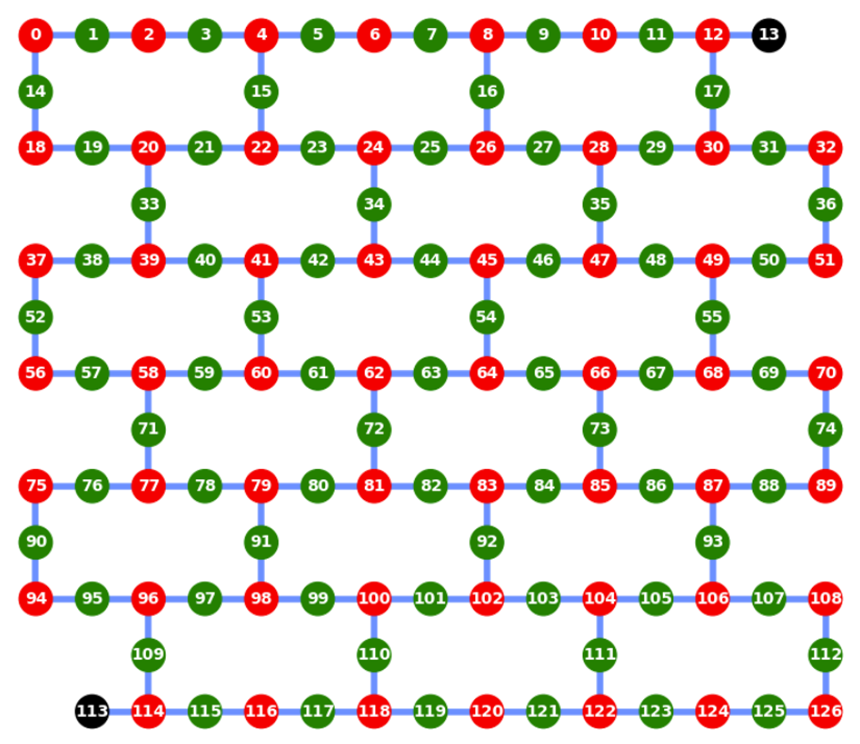
それぞれの量子ビットの色が分かれていますが、赤の部分が先ほどのGHZ状態として残す部分、緑の部分がそれをエンタングルを解除した部分になります。見た目通りで交互に織り込まれるようにGHZ状態とそれを解除した状態が残っています。この間の量子ビットはスタビライザーを作っていることに相当します。スタビライザーはエラー訂正の考え方で出てきて、隣り合う両方の状態に応じ自身の状態が変化し、エラーが起きているかどうかを判断するための量子ビットになります。
ここではエンタングルを解除した状態をアンエンタングルという言葉で表現しています。要は一回仲間に入れたんだけども、その仲間からは外したということですね。
言葉では難しいのですが、やっていることは、緑の量子ビットに先ほどと逆のことをすれば良いのです。
for n in stabilizer_qubits:
qc.cx(0,n)
ここでは、stabilizer_qubitsは事前に定義されており、緑の量子ビットの番号が全て格納されています。実はこれだけで終わりです。
回路を短くする
さて、この後の問題として、実機にリクエストして帰ってきた結果を元に状態がどれだけキレイにできていたかを測るための算出方法をコードで書くなどの問題があるのですが、それ自体は難しくも無いのと、改良にはあまり関係ないので割愛します。ここからはこのExercise1と2の回路を改良していくプロセスを紹介します。
回路の長さを表す指標Depth
まずDepthについて解説します。Depthとは回路の長さを表す指標です。要は量子回路を書いたときに何ステップで終わらせられるかというクリティカルパスの長さをさします。
$n=4$のGHZ状態の場合を考えてみましょう。
この回路のDepthは4です。一番上の量子ビットから他の量子ビットに伸びている足に当たる部分の処理が、シリアルに行われているためです。
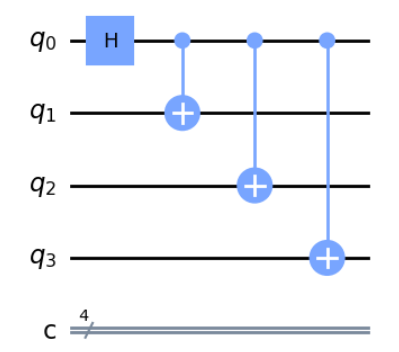
プログラミングが得意な人は気付いたと思いますが、実はこの回路はもう少し改良できます。
それは以下のようにすることです。こうすれば、Depthは3で済みます。
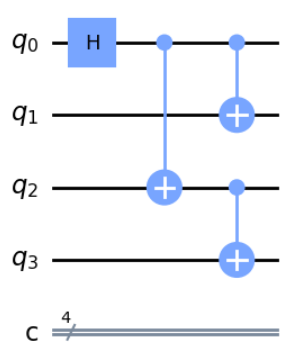
これは3回目の処理の所で、それぞれ独立の量子ビット間で処理が行われるため、並列に処理できることを表しています。
このような形で処理の流れを工夫することでDepthを短くすることができるので、そういった道筋を探すことをしています。
Depthを短くすることは量子計算において非常に重要です。特に、処理ステップが多いとそれだけノイズが乗りやすくなりますし、Depthは計算時間にも影響します。計算時間が延びるとそれだけ量子状態が不安定になりエラーがますます乗りやすくなります。つまり、量子計算は如何にして少ないステップで処理をできるように回路を工夫するかということで計算性能そのものに多大な影響を与えるため、常にケアしなければいけません。
上記の結果ではどうなっているのか
では、上に書かれているExercise1と2の結果をそのまま使うとDepthがどうなるかなのですが、単純計算でExercise1でDepth=127、Exercise2でDepth=73となり、合わせてDepth=127+73=200となります。ただし、実際に実機で動かすためには書いたコードがそのまま動くわけではなくトランスパイル(Transpile)という処理を行った上で実機で動かします。
トランスパイルとはコンパイルのような処理と似ています。コンパイルがその言語で書いたコードを機械で動かすように翻訳する作業を指しますが、トランスパイルでは、その量子デバイス実機の構造に合わせて、実機で使える回路の処理だけで再構成し直す処理を行っています。この過程では複数の処理を1つでまとめて処理させたり、処理の最適化も併せて行っています。
実際には最初に提示した回路のままトランスパイルを行うと、Depth=5000以上のコードに翻訳されていまいます。 これが長いかどうかは計算させてたい内容にもよるのですが、元のコードで書いたときのDepth=200に比べて爆発的に膨れ上がっていることを考えると健全ではないことはわかると思います。つまりまだ改良の余地があるのではないか、と考えるわけです。
どこまで改良できるか
これは公式に明言されたわけではないのですが、どうやら56までは縮められる余地があるようです。
これを見て火がついてしまい、開催期間中に頑張って改良を進めました。
Exercise2を改良する(Depth=2にする)
では、最初に改良が思いつくのはExercise2の方です。こちらは先ほど量子ビット0を起点にCNOTを他の量子ビットにかけていましたが、このやり方はどう考えてもスマートではありません。
目標とする状態をもう一度見てみると、隣合う量子ビットで折りたたまれているので、その構造に着目しましょう。
つまり、隣り合う量子ビットのGHZ状態になった方を起点に隣の量子ビットをアンエンタングルしすれば、並行してできることがわかると思います。例えば、量子ビット0を起点に量子ビット1をアンエンタングルするのと並行して、量子ビット2を起点に量子ビット3をアンエンタングルするのは同時に実施可能ということです。それさえわかれば、隣り合う量子ビットのどっちかを起点にして、残りをアンエンタングルするというのを漏れなく実施するだけということです!
ということで、こんな感じに書いてみました!!!!
def deentangle_qubits():
qc = QuantumCircuit(quantum_register, classical_register)
####### your code goes here #######
qc.cx(0,1)
qc.cx(0,14) #
qc.cx(2,3)
qc.cx(4,15) #
qc.cx(4,5)
qc.cx(6,7)
qc.cx(8,16) #
qc.cx(8,9)
qc.cx(10,11)
qc.cx(12,17) #
qc.cx(12,13)#10
qc.cx(18,19)
qc.cx(20,33) #
qc.cx(20,21)
qc.cx(22,23)
qc.cx(24,34) #
qc.cx(24,25)
qc.cx(26,27)
qc.cx(28,35) #
qc.cx(28,29)
qc.cx(30,31)#20
qc.cx(32,36) #
qc.cx(39,38)
qc.cx(43,42)
qc.cx(41,40)
qc.cx(47,46)
qc.cx(45,44)
qc.cx(51,50)
qc.cx(49,48)
qc.cx(37,52) #
qc.cx(41,53) #30
qc.cx(45,54) #
qc.cx(49,55) #
qc.cx(56,57)
qc.cx(58,71) #
qc.cx(58,59)
qc.cx(60,61)
qc.cx(62,72) #
qc.cx(62,63)
qc.cx(64,65)
qc.cx(66,73) #
qc.cx(66,67)#40
qc.cx(68,69)
qc.cx(70,74) #
qc.cx(77,76)
qc.cx(81,80)
qc.cx(79,78)
qc.cx(85,84)
qc.cx(83,82)
qc.cx(89,88)
qc.cx(87,86)
qc.cx(75,90) #50
qc.cx(79,91) #
qc.cx(83,92) #
qc.cx(87,93) #
qc.cx(94,95)
qc.cx(96,109) #
qc.cx(96,97)
qc.cx(98,99)
qc.cx(100,110) #
qc.cx(100,101)
qc.cx(102,103)#60
qc.cx(104,111) #
qc.cx(104,105)
qc.cx(106,107)
qc.cx(108,112) #
qc.cx(114,115)
qc.cx(114,113)
qc.cx(116,117)
qc.cx(118,119)
qc.cx(120,121)
qc.cx(122,123)#70
qc.cx(124,125)
return qc
著者はプログラミングスキルが3流なので、この処理をキレイに書く方法が思いつきませんでした。だったら、力業で書いた方が早そうだったので、書き出したらこれでトランスパイル前の時点でDepth=2を達成しました。
GHZ状態は54個に対して、それ以外は73個あるので、同じGHZ状態を起点にしてアンエンタングルするには2回は実施しないといけないGHZ量子ビットが存在するので、これは仕方ありません。(鳩ノ巣論法みたいなものです)
いずれにせよこれが、Exercise2では最小のステップになります。これは多くの参加者がすぐに気付いたと思われます。
Depthが増える理由①(隣合わない量子ビット間でのCNOTはDepthが増えがち)
実はこの修正は、思わぬ形で効果をもたらします。
物理的に繋がっていない(隣あっていない)量子ビット間でCNOTを書いた場合、トランスパイルするとその間を介して同じ状態になるように調整が走ります。その結果Depthが増えることになります。
具体的には以下を見てください。量子ビット0と1は隣あっていますが、量子ビッチ0と2では隣合っていないため、その状態を整合性が合うようなに間にCNOTや単一量子ビットの処理を入れ込むように書き直しています。これはどう見てもDepthが増えています。これはまだ物理的に近い量子ビット同士でやっているのでこのDepthで済んでいますが、遠くなれば遠くなるほどこのDepthが増えるのは容易に想像できると思います。つまりこのような物理的なレイアウトは十分に意識して回路を書かないと、知らない間に回路が長くなり、計算結果が使い物にならない結果になってしまいます。
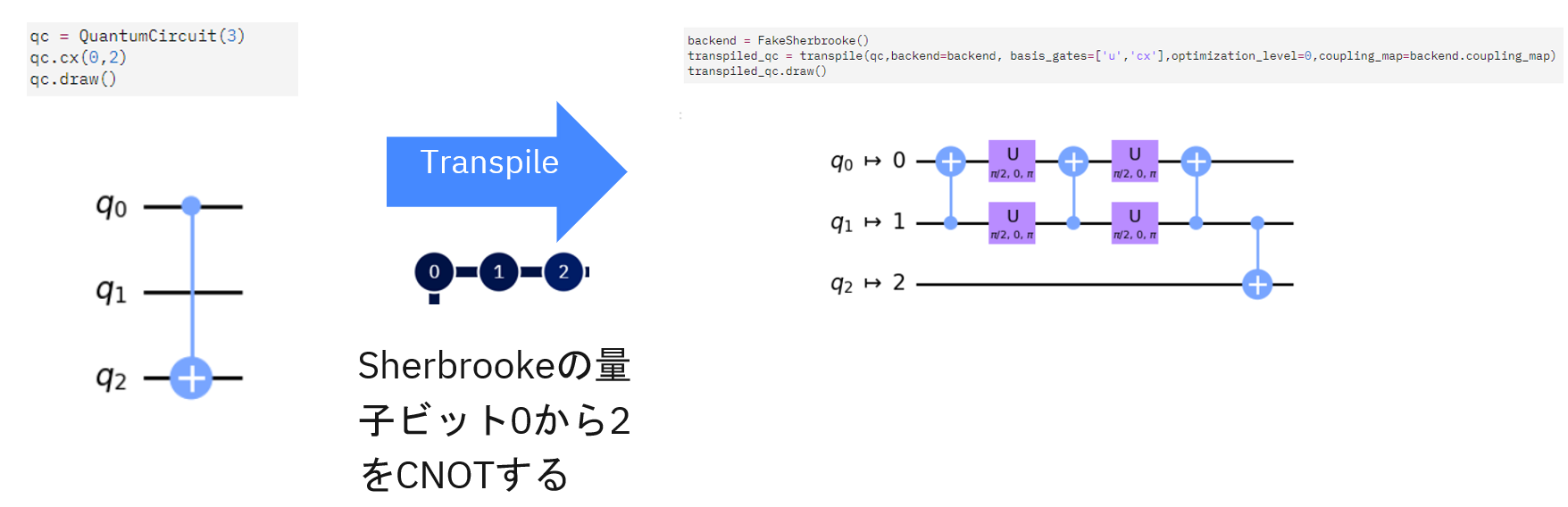
これはExercise1、2ともにそのことを考慮していないため、回路が異常に長くさせられていたことになります。
Exercise1と改良する
実はこちらの方が圧倒的に実装が難しいです。ただ、やっていることは単純でパズルのような話ではありますから、内容は理解しやすいと思います。
直前の話を踏まえて、隣合うもの同士を次々にGHZ状態を伝搬させていけば改良できる道筋が立ちそうです。
ではもう一度実機のレイアウトを見てください。 どこを起点にするのが良さそうでしょうか?
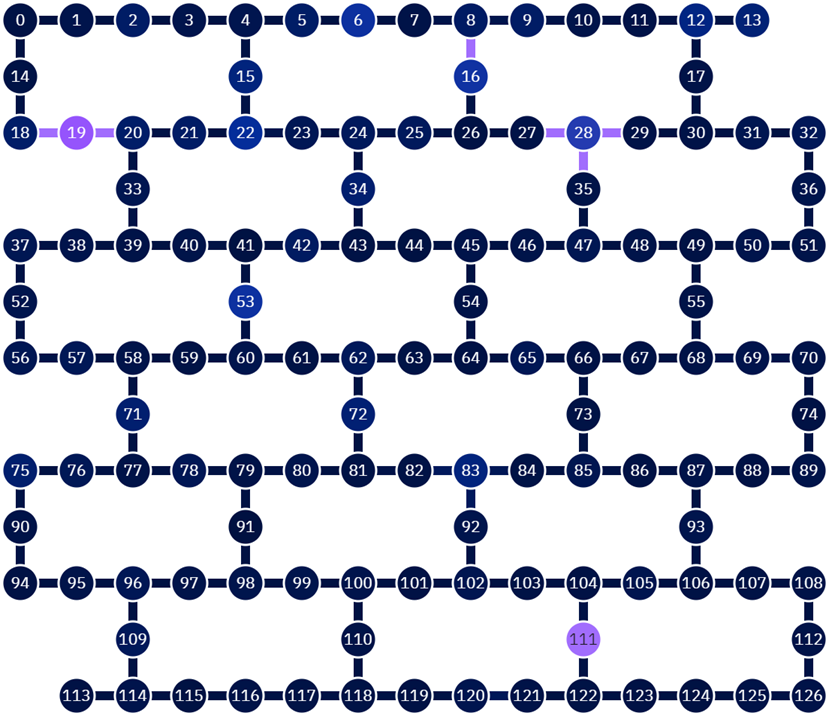
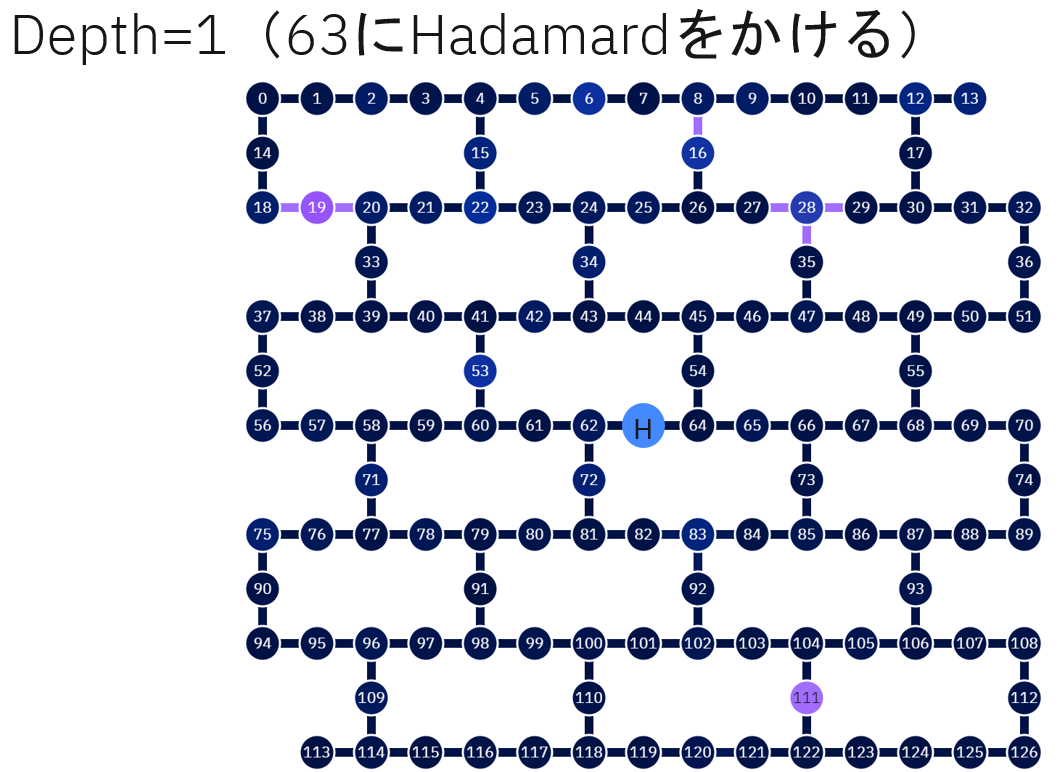
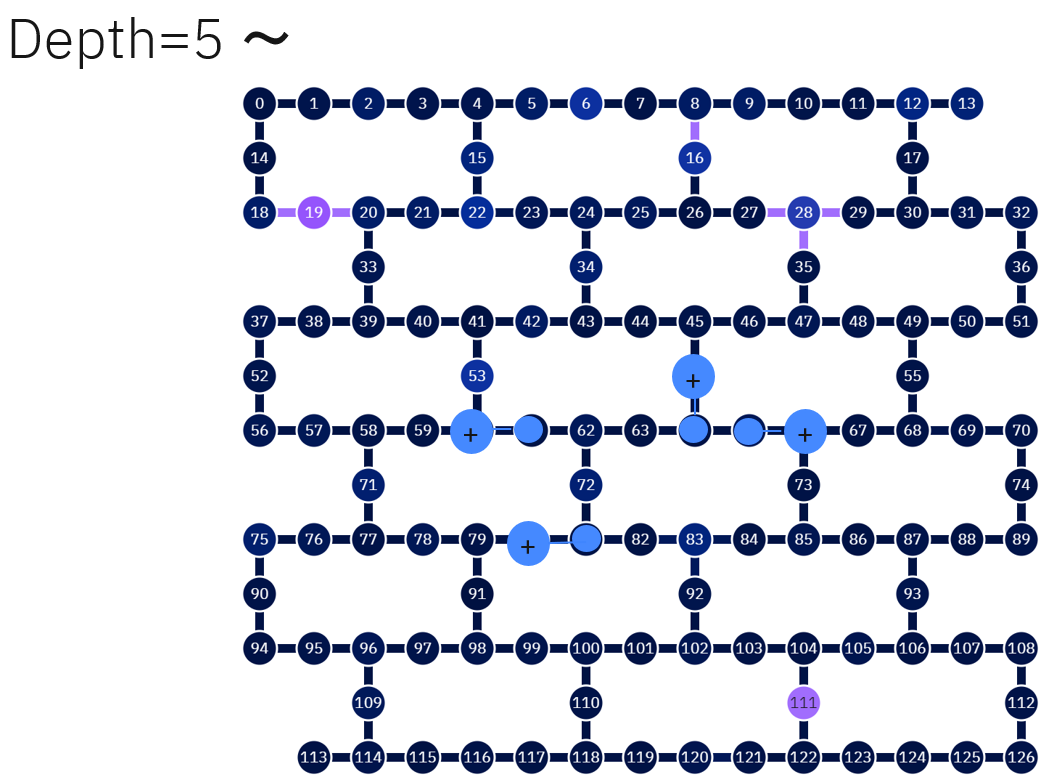
先ほどは量子ビット0から作ってみましたが、ここからだと量子ビット126まではすごく遠いです。となると、真ん中辺から始めるのが良さそうでしょう。今回だと量子ビット63が一つ基準になりそうです。
そこから作ってみると次のような形でしょうか。
Depth=1
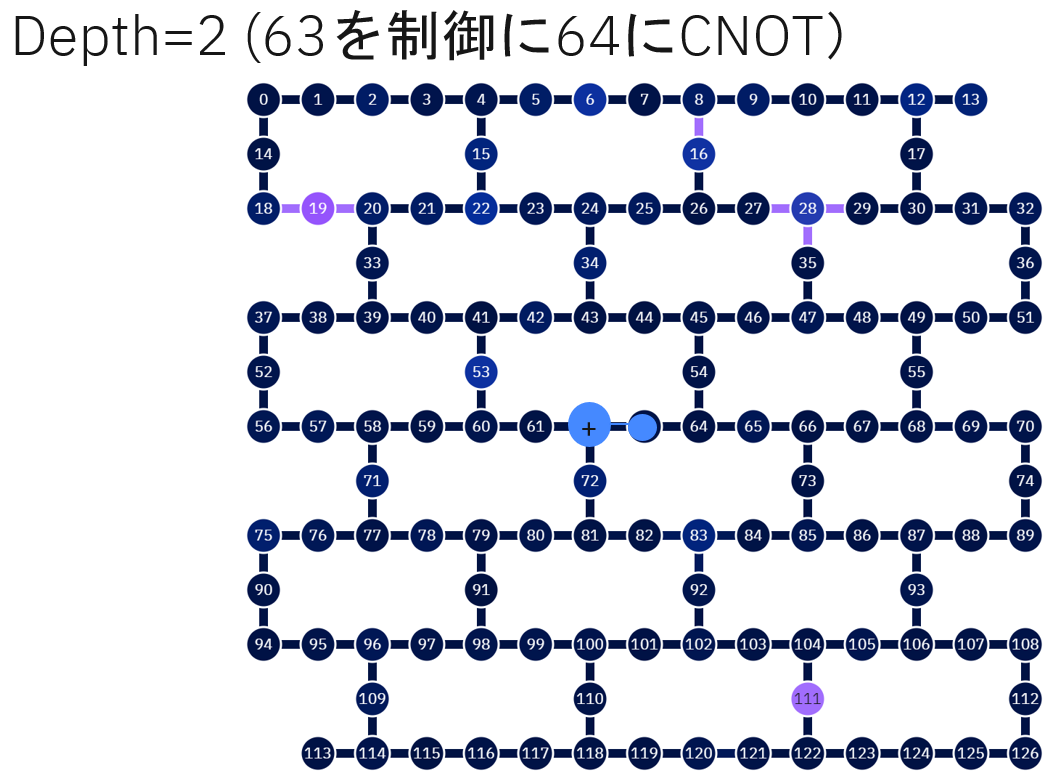
Depth=2
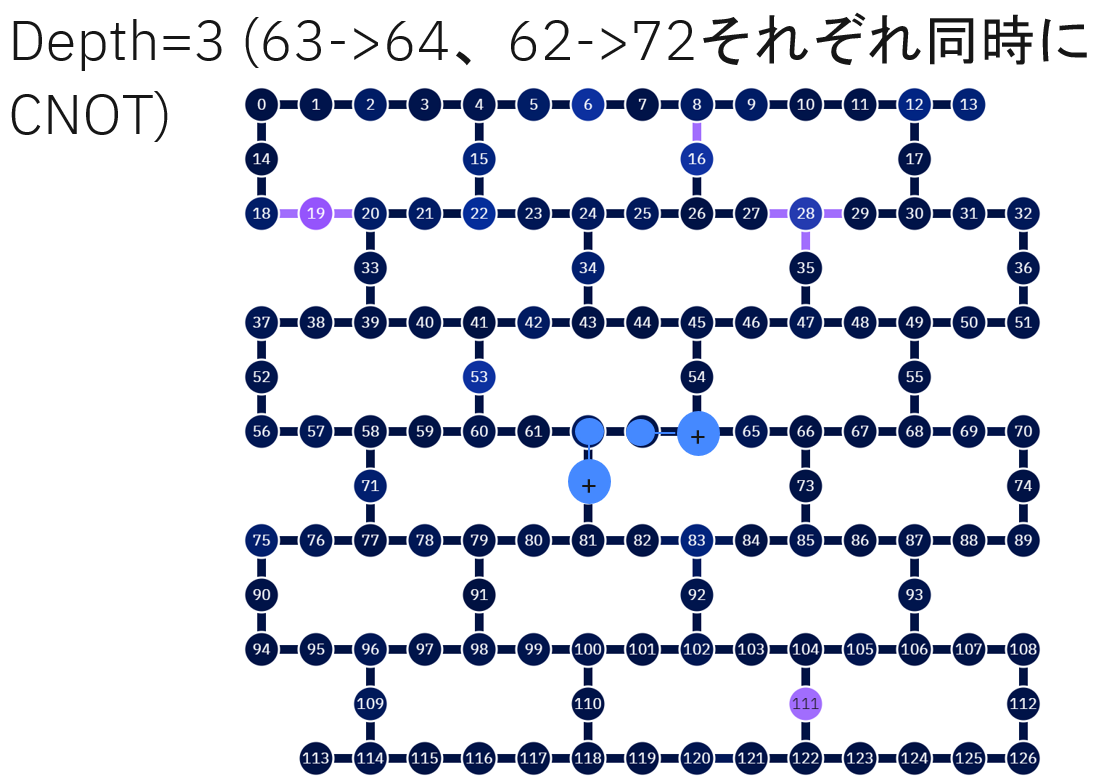
Depth=3
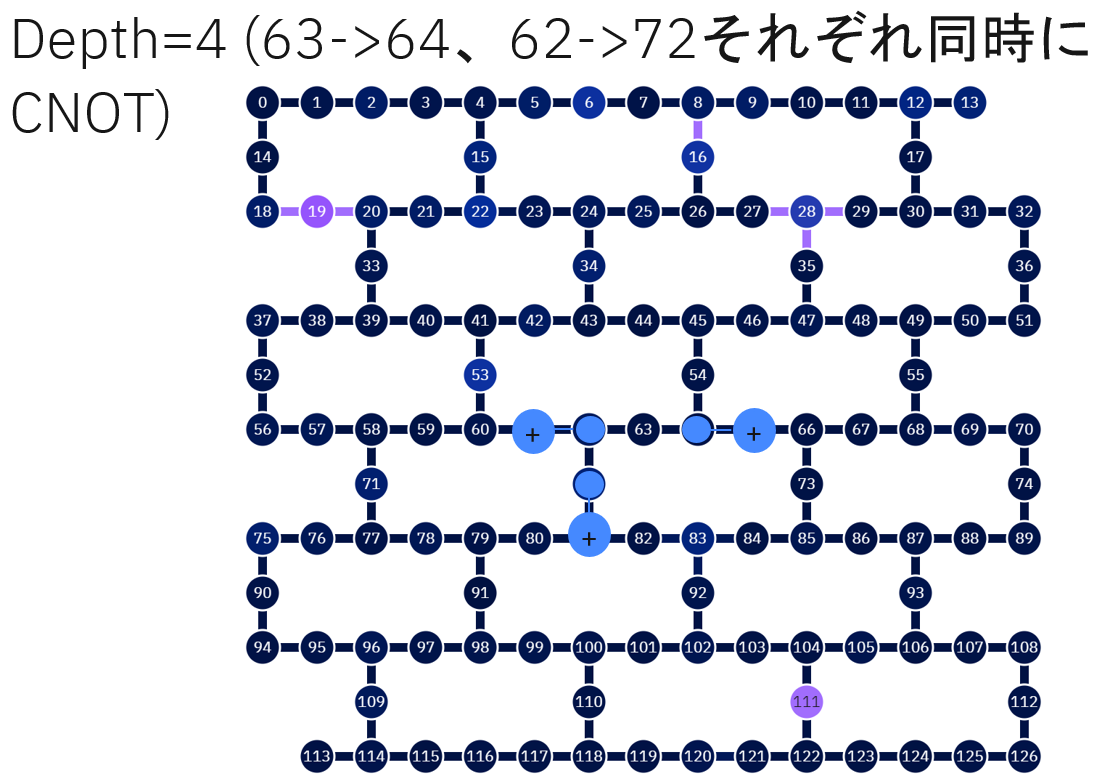
Depth=4
Depth=5~
もうここからは同じことの繰り返しなので、ひたすらCNOTでGHZ状態を電波させていきます。
クリティカルパスに注意する
ここは量子ビット63を起点にしましたが、そこから最も遠い量子ビットを意識しておく必要があります。
今回は量子ビット2と124が該当します。ここを意識する必要があります。ただし、これらは処理の流れ的には等価のクリティカルパスではなく、処理の順番によって片方が真のクリティカルパスになります。
上記のDepth=2と3の処理で、左に行く方を先に行っているで、右に行く方が一手遅れています。つまり、右側の方の量子ビット124が一番時間がかかるため、そちらが真のクリティカルパスになります。そこに注意しておく必要があります。
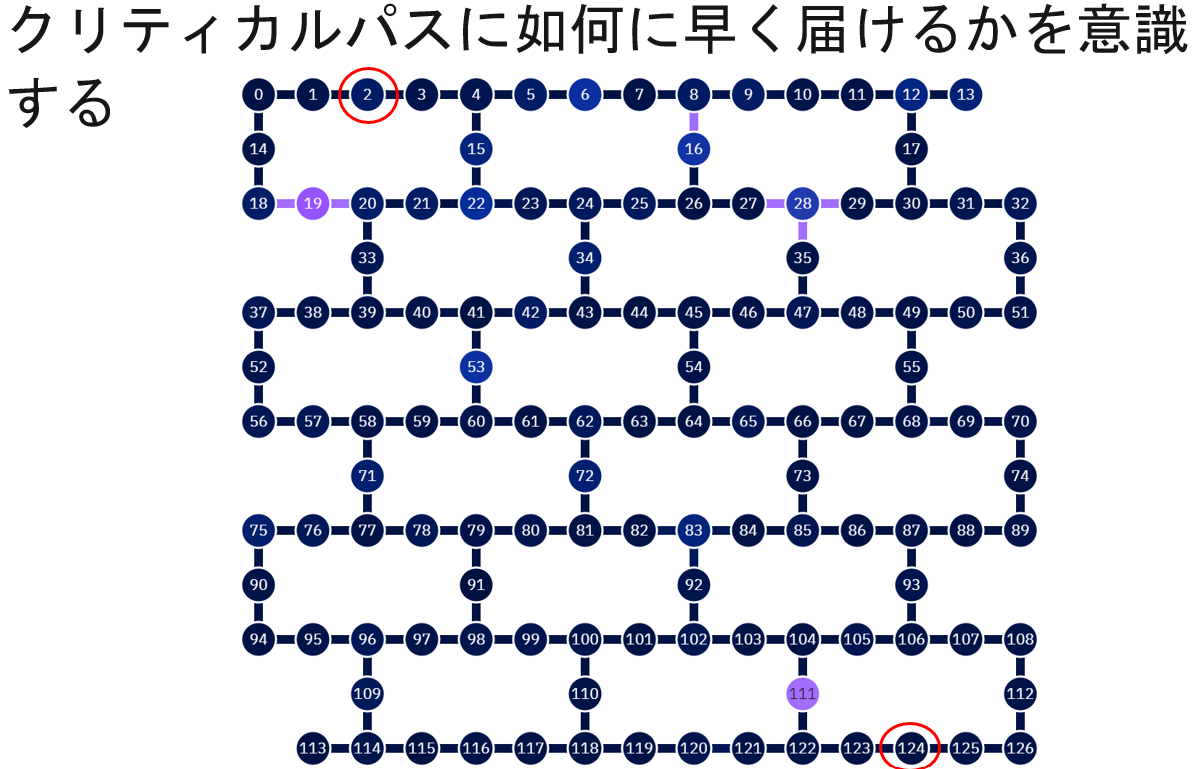
それを含めて、これをコードに落とし込むとこんな感じになります。
def generate_ghz127():
qc = QuantumCircuit(quantum_register, classical_register)
#### depth = 18 -> 55
# depth = 1
qc.h(63)
#depth = 2
qc.cx(63,62)
#depth = 3
qc.cx(63,64)
qc.cx(62,61)
#depth = 4
qc.cx(62,72)
qc.cx(64,65)
#depth = 5
qc.cx(64,54)
qc.cx(61,60)
qc.cx(72,81)
qc.cx(65,66)
#depth = 6
qc.cx(54,45)
qc.cx(60,53)
qc.cx(81,80)
qc.cx(66,73)
#depth = 7
qc.cx(60,59)
qc.cx(81,82)
qc.cx(45,46)
qc.cx(45,44)
qc.cx(66,67)
qc.cx(53,41)
qc.cx(59,58)
qc.cx(80,79)
qc.cx(82,83)
qc.cx(46,47)
qc.cx(44,43)
qc.cx(73,85)
qc.cx(67,68)
qc.cx(41,40)
qc.cx(41,42)
qc.cx(58,57)
qc.cx(58,71)
qc.cx(79,91)
qc.cx(79,78)
qc.cx(83,92)
qc.cx(83,84)
qc.cx(47,35)
qc.cx(47,48)
qc.cx(43,34)
qc.cx(85,86)
qc.cx(68,55)
qc.cx(68,69)
qc.cx(40,39)
qc.cx(57,56)
qc.cx(71,77)
qc.cx(91,98)
qc.cx(92,102)
qc.cx(35,28)
qc.cx(48,49)
qc.cx(34,24)
qc.cx(86,87)
qc.cx(69,70)
qc.cx(39,33)
qc.cx(39,38)
qc.cx(56,52)
qc.cx(77,76)
qc.cx(98,97)
qc.cx(98,99)
qc.cx(102,101)
qc.cx(102,103)
qc.cx(28,27)
qc.cx(28,29)
qc.cx(49,50)
qc.cx(24,23)
qc.cx(24,25)
qc.cx(87,93)
qc.cx(87,88)
qc.cx(70,74)
qc.cx(33,20)
qc.cx(38,37)
qc.cx(76,75)
qc.cx(99,100)
qc.cx(103,104)
qc.cx(27,26)
qc.cx(29,30)
qc.cx(50,51)
qc.cx(23,22)
qc.cx(93,106)
qc.cx(88,89)
qc.cx(97,96)
qc.cx(20,19)
qc.cx(20,21)
qc.cx(75,90)
qc.cx(100,110)
qc.cx(104,111)
qc.cx(104,105)
qc.cx(26,16)
qc.cx(30,17)
qc.cx(30,31)
qc.cx(51,36)
qc.cx(22,15)
qc.cx(106,107)
qc.cx(96,109)
qc.cx(96,95)
qc.cx(19,18)
qc.cx(90,94)
qc.cx(110,118)
qc.cx(111,122)
qc.cx(16,8)
qc.cx(17,12)
qc.cx(31,32)
qc.cx(15,4)
qc.cx(107,108)
qc.cx(109,114)
qc.cx(18,14)
qc.cx(118,119)
qc.cx(118,117)
qc.cx(122,121)
qc.cx(122,123)
qc.cx(8,9)
qc.cx(8,7)
qc.cx(12,11)
qc.cx(12,13)
qc.cx(4,5)
qc.cx(4,3)
qc.cx(5,6)
qc.cx(108,112)
qc.cx(14,0)
qc.cx(121,120)
#qc.cx(123,124)
qc.cx(9,10)
qc.cx(0,1)
qc.cx(3,2)
qc.cx(112,126)
qc.cx(126,125)
qc.cx(125,124) # こちらの方がトランスパイル後に短くなる
qc.cx(114,115)
qc.cx(114,113)
qc.cx(115,116)
return qc
はい、もうベタ書きです。何度も言いますが、著者はプログラミングを得意としていないので、力業で考えるしかできませんでした。きっと優秀なプログラマーであれば綺麗で洗練されたコードで書き出すことでしょう。自分にも無理です。
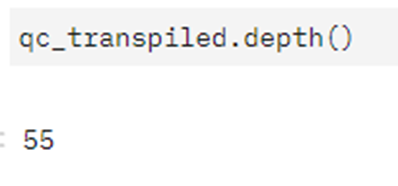
ただ、このコードであればトランスパイル前であれば、Depth=18で済みます。 結果、先ほどのExercise2の改良と合わせてトランスパイル後Depth=55を達成しました。先ほど56までしか見たことないということでしたが、それよりも回路よりもさらに圧縮することに成功したのです!
実際には自分を含めて3人ぐらいが到達していた形跡があります。
ただ、この改良を行っていたときに1つ面白いことが起こりました。コードの最後の方にCNOTを1つだけコメントアウトしている所があることに気付いたでしょうか?これはあえて残しています。
実は、量子ビット124にCNOTするときに、123->124よりも、125->124とした方が、トランスパイル後にDepthが減ったのです。最初はわからなかったのですが、終わった後に色々調べていたら重要な事実が判明しました。
Depthが増える理由②(量子ビット間の繋がりには直接CNOT可能な向きがある)
書いてある通りなのですが、実は量子ビットのCNOTには直接CNOTが可能な向きが存在しています。
これは今回の実機と同じibm_sherbrookeで量子ビット0->1と1->0で実施、トランスパイル後にどう変化がするかを示した例になります。見てわかるように右側は特に変化は無いのですが、左側はCNOTの向きを変えつつ前後にゲートを追加しています。これはCNOTの向きが決まっているので、それに合わせて調整した結果ということになります。
実はこれについては、公式には明言されておらず、大会中には情報提供されていない内容でした。実際には以下のように向きを含めてレイアウトが決まっていたのです!
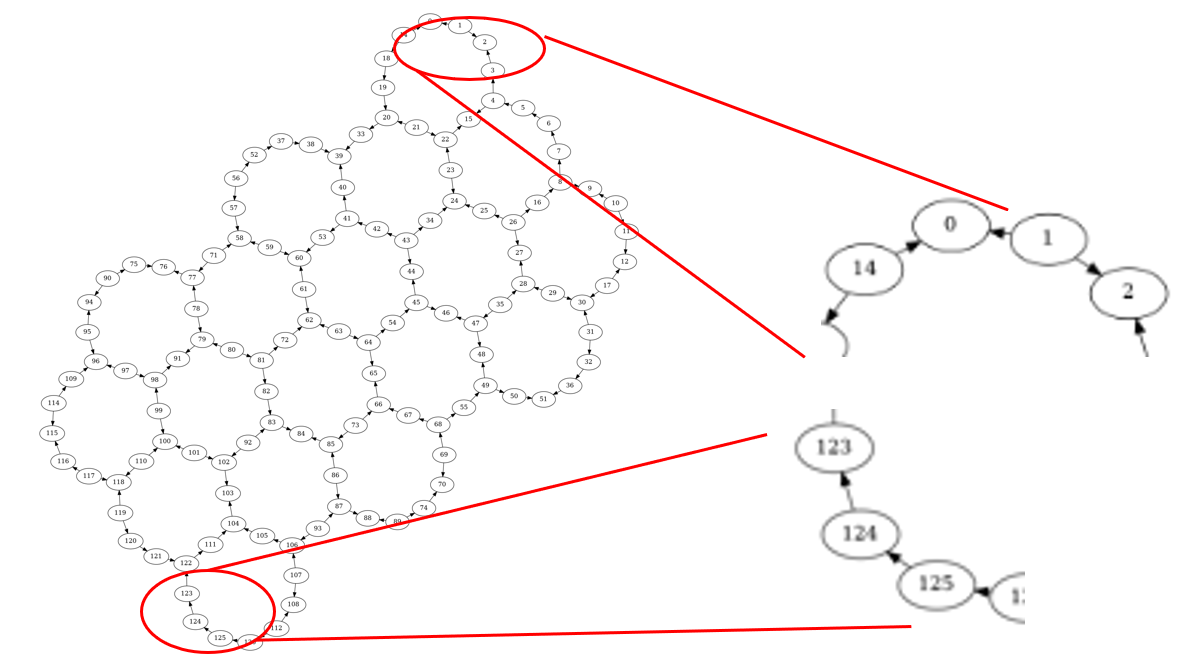
見ていると、1->0に矢印が出ていて、矢印の元が制御ビット、先がターゲットビットになっていますし、上記の例に沿ったトランスパイルが行われていたのです。
そこで、量子ビット124に着目すると、123->124は向きが逆になっていて、125-124は正しい向きになっています。これが、最後の決め手になったというのが、オチになっています。
実際にはこのレイアウトも意識して回路を書くというのが実機で動かす上では非常に重要になるということを意識しておかないといけない、という重要な教訓を得ることができました。
回路を描画してみたら・・・
はい、もう人間が見るのはムリですね。かなり短いはずですが、すでにこれなので、今後量子ビットが増えたとき、どうやってデバッグすれば良いのか、今から絶望感が漂っています。。。
さらに回路は縮められる?
自分が書いた後にいろいろ調べた所、トランスパイル後にDepth=52まで行ったという人もいるようです。この人がいたので、最初に述べたように2番目ぐらい短いという表現を使いました。
BFS(幅優先探索)という数理最適化の手法で、解を得たようです。おそらくこのあたりも考慮して定式化を行っているはずです。方法論的にすぐには実装するのは無理ですが、確かにまだ縮められる道筋はあるように思えました。
いつか、こんな風にスマートに解けるプログラミング力を身に着けたいです!
最後に
今回も1週間という時間ではありましたが、楽しむことができました。特にこの最後の問題は問題自体がオープンにされてから3日間しかなかったのですが、かなり良好な結果を出せて個人的には満足です。
ただ、今回は順位が付かなったで若干残念ですし、他の人も解答も見たかったので、それを実施して欲しかったなというのが心残りです。自分も世界に対してマウント取りたかったです。なので、こうやって非公式ではありますが自分でマウント取るようにしました。(自己顕示欲の塊)
おそらく次は秋になると思いますが、その時も頑張って、去年の7位を上回れるように頑張りたいと思います。
なお、この記事は社内勉強会で発表した内容をベースにしています。公開しておきますので、ご覧になりたい方はどうぞ。資料を見ながら解説を読んでいただくと流れがわかりやすいかもしれません。
https://speakerdeck.com/ayumu0118/ibm-quantum-challenge-spring-2023-lab5jie-shuo
参考文献
Generating GHZ state on IBM device ~A look into the final lab of IBM Quantum Spring Challenge 2023 ~