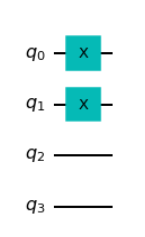IBM Quantum Challenge 2021（2021年5月）を振り返る（速報版）

はじめに / IBM Quantum Challengeとは

IBM Quantum Challengeとは、IBMが主催する量子コンピュータープログラミングコンテストです。
ここ２年ほどは５月と１１月に、半年に１回ペースで開催されています。
この中では問題が複数与えられていて、いくつかの問題には基準スコア、多くの場合は量子回路の基準コストが設定されていて、それを下回るように効率的な量子回路を組む必要があります。やり込み要素もあり、スコアを競うこともできます。特に最後の問題は難問で、クリアするのも大変ですが、クリアしたら制限時間まで回路を効率化してスコアを更新することができます。
全て解ききるには、ある程度の専門性は必要ではありますが、初心者でも取り掛かれるように教育的なコンテンツとしても使えて、丁寧な導入が成されています。順を追って解いていくことで理解が深まるように内容が整理されています。

今回は、2021/5/20-27に開催されたIBM Quantum Challenge 2021に参加し、何とか完走し、最高スコアが出せましたので、各exerciseの解説を書いてみます。各章の前置き部分の解説は基本的にはしませんので、そちらはコンテンツを読んでください。

問題は全部で5問です。GitHub上にも公開されていますので、こちらのネタバレを見る前に一度自力で解いてみてください。今回のはこれまでと比べて、導入の難易度がやや高く感じました。一部問題については、一番下にある過去問を見てみると、ヒントがあるかもしれませんので、そちらも見てみてください。

今回は多くの人が最高スコアまで到達し、自身も到達できました！（1st Prizeには参加者の15%ほどである200人以上が到達したようですので、特別な結果ではありません）

ここでの回答はあくまで著者本人が考えた思考過程と提出した回答になりますので、あくまで一例とお考えいただいた上でご参照ください。速報での解説のため、説明に穴があることが十分理解していますので、今後加筆修正する予定でいます。初期の段階ではご了承ください。

近い将来に公式の回答と参加者の独自の回答はこちらに公開されるようです。（5/30日時点では公開されていない）
https://github.com/qiskit-community/ibm-quantum-challenge-2021/tree/main/solutions%20by%20authors
https://github.com/qiskit-community/ibm-quantum-challenge-2021/tree/main/solutions%20by%20participants

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

exercise1（Toffoliゲート）

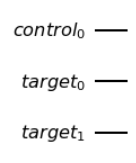
Toffoliゲートとは、２つの制御ビットと１つのターゲットビットからなり、２つの制御ビットの両方が|1>の場合にNOTゲート（Xゲート）を作用させるものでした。CCXゲートとも呼ばれます。

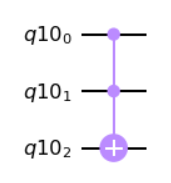
一覧にして書くとこんな感じです。

制御ビット１ (q10_0)	制御ビット2 (q10_1)	入力ターゲットビット　(q10_2)	出力ターゲットビット(q10_2)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

線型代数的に、行列で表現するとこんな感じです。一番右下の所に注目です。

今回の問題は、**「ToffoliゲートをCX、SX、X、Rzゲートのみで再構築せよ」**というのものです。
このような問題を出す背景としては、一般的にCCXゲート自体は、Qiskitにもコードとして提供されているのですが、実機に投げる際には任意のゲートを実現する物理現象を制御することが難しいので、より物理的に実現が簡単でエラーが少ないゲートに分解する処理を内部的にしてから実機で実行させています。この問題は、実機に優しい回路を組んでみてね、ということをメッセージでもあります。

まず、この問題を解こうと思う際、最初は指定のゲートを使うかどうかは忘れて、どんなゲートで再構成できるかを考えます。それから、必要に応じて指定のゲートに置き換えていくという戦法で行きます。

まず、このToffoliゲートの分解は以下のように分解できることを知っていないと実質的に解けない問題かもしれないですね。。wikipediaにも書いてある事実として利用できます。

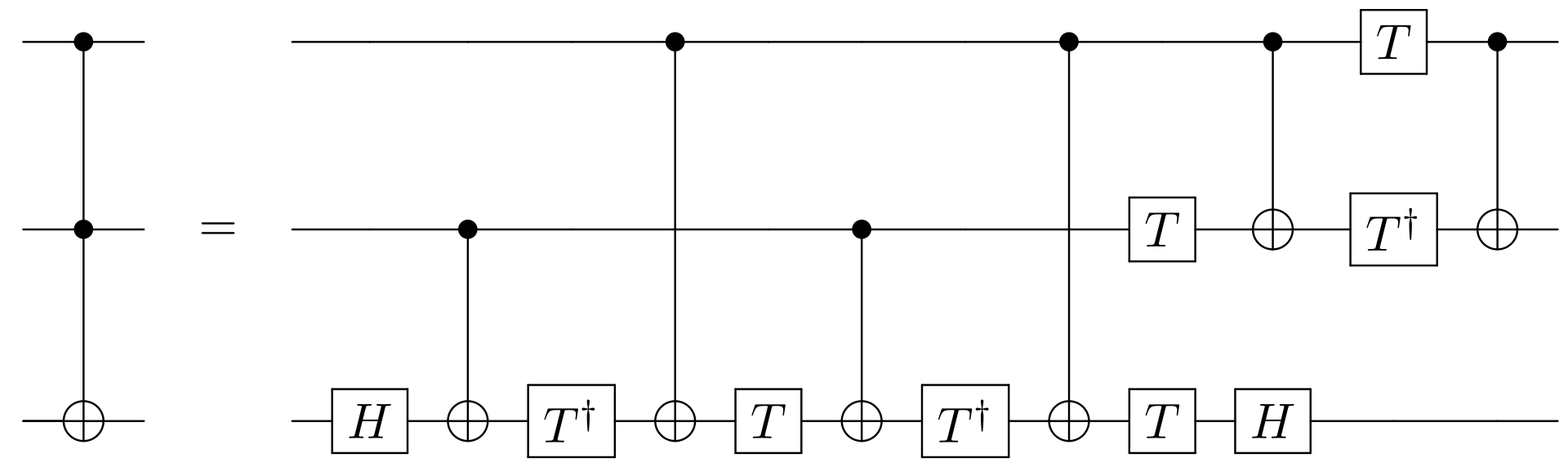
公式からもさりげなくヒントが公開されているのでこれを見つけられないと詰む人続出だったと思います。
https://github.com/qiskit-community/ibm-quantum-challenge-2021/blob/main/hints.md

見ているとCXゲートは使われていますが、それ以外にTゲート（T†ゲート含む）やHゲートがあり、それらを指定のゲートに置き換えることを考える必要がありそうです。

問題の前の前置きにいくつかヒントが書いてありますので、それを眺めてみます。
すると、HゲートをSXゲート（式としては$\sqrt{X}$と表現します）とRzゲートで構成する方法が提示されていますので、それを使いましょう。

H=Rz(\frac{\pi}{2})\sqrt{X}Rz(\frac{\pi}{2})

つぎにTゲートはRzゲートの特定の角度$\pi/4$を入れたときのものと同等になります。つまり

T=Rz(\frac{\pi}{4})

T†ゲートは角度を反対側に回転させたものと考えますので、$T^{\dagger}=Rz(-\frac{\pi}{4})$となります。
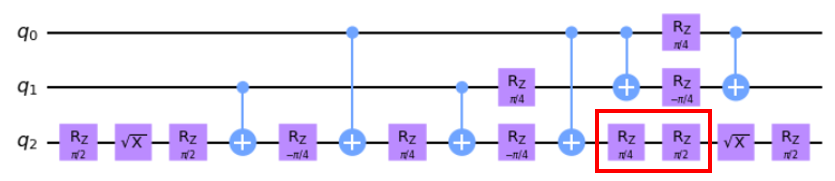
という感じで、上記の回路をそれぞれ置き換えると、以下のようになるはずです。

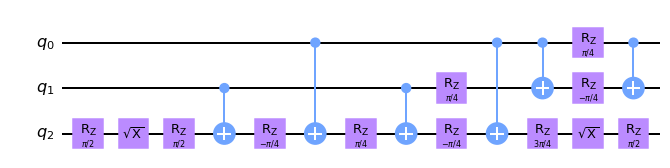
いったんこれでも通るのですが、もうちょっとだけゲートを削除できます。赤い枠の所に注目してください。ここは、Rzゲートが２回続いていますね。このとき、２つの角度を足した１つのゲートに置き換えることが可能です。それを踏まえると以下のようになります。

１つのゲートになったところは、$\pi/4+\pi/2=3\pi/4$になりますので、上記のように書けることになります。

これはコスト72（=CNOT（コスト10）×6個+Rzゲート（コスト1）×10 + SXゲート(コスト1)×2
）で通る回路になります。

exercise2（Shorのアルゴリズム）

第２問はShorのアルゴリズムに関する問題です。Shorのアルゴリズムは古典よりも高速に素因数分解できるアルゴリズムです。
今回は、$ 13y$ mod $ 35 $ （13の倍数を35でわったときの余り）を実装した回路を組んでみようという話になります。
最初にこの問題の背景を見ておきましょう。
この問題では次のようなユニタリ演算子$U$を考えます。$$ U\ket{x} = \ket{13x\pmod{35}}$$
これは入力$\ket{x}$にユニタリ演算子を作用させると$x$を13倍して35で割った余りにラベルされた状態と同じになるということを言っています。$\ket{1}$という状態に$U$を作用させると、$$U\ket{1}=\ket{1×13\pmod{35}}=\ket{13}$$になりますね。ここで作れた状態にもう一度$U$を作用させてみましょう。すると$$UU\ket{1}=U\ket{13}=\ket{13×13\pmod{35}}=\ket{169\pmod{35}}=\ket{29}$$となります。もう一度$U$を作用させる$${U\ket{29}}=U\ket{29×13\pmod{35}}=\ket{377\pmod{35}}=\ket{27}$$
です。しつこいようですが、もう一度$U$を作用させると$$U\ket{27}=\ket{27×13\pmod{35}}=\ket{351\pmod{35}}=\ket{1}$$となり、最初の状態に戻ることがわかります。これは、周期4でサイクルしていることになります。

このような背景から、初期状態が同じなら４パターンの状態以外は出現しないため、それを最もシンプルな２進数表記の00、01、10、11の４つのエンコード（対応）する形で問題を超簡略化していることを前提にして解くようになっています。

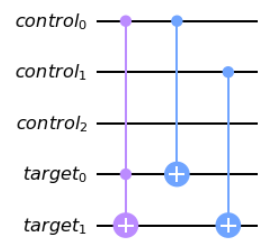
2-a

この問題ですが、各ビットの0と1がどう変化しているかというルールに着目して解けば良いです。まず目につくところとしては、右側のビットは入力から値が反転している（0と1が入れ替わっている）ことがわかります。これはXゲートをかけることで対応できそうです。左側のビットはどうでしょうか？何か法則はあるでしょうか？入力の右側のビットを左側のビットに足し込むと出力の右側の値になっているのがわかるでしょうか？右側のビットの値が入力の状態でやる必要がありそうです。以上のことから、　少し順番に気を付けて、以下のような手順で進めると上手く行きそうです。
①左側のビットの値を右側のビットの値に足し込む
②右側のビットを反転させる（=値を足し込む）

では①はどうすればよいか。自分のビットの値を相手に加えるのはCXゲートが担えますので、それを使いましょう。②は単純にXゲートだけで実現できます。このことから、CXゲートの後にXゲートを作用させればいいですね。
さて、さて少し問題に注意が必要です。この問題では３量子ビットを使うように指定があり、そのうち１つは制御ビットとするように指示があります。それらに残りの２つの量子ビットがターゲットになるようにしないといけません。つまり、CXゲートはCCXゲート（Toffoliゲート）に、XゲートはCXゲートに書き換える形で作ることになります。
以上を踏まえてやっと答えが出せます。

ex2a

from qiskit import QuantumCircuit
from qiskit import QuantumRegister, QuantumCircuit
c = QuantumRegister(1, 'control')
t = QuantumRegister(2, 'target')
cu = QuantumCircuit(c, t, name="Controlled 13^x mod 35")

# コードを記入ください - 開始
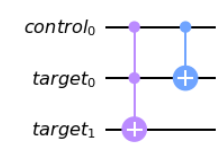
cu.ccx(c[0],t[0],t[1])
cu.cx(c[0],t[0])
# コードを記入ください - 終了

cu.draw('mpl')

これが答えになります。この問題はちょっとしたパズルですね！

2-b

これも同じように各ビットが入力と出力でどうなっているかを眺めてみましょう。すると、これは左側のビットだけが反転していることに気づきましたか？右側は特に変わっていないですね。

ex2b

c = QuantumRegister(1, 'control')
t = QuantumRegister(2, 'target')
cu2 = QuantumCircuit(c, t)
# コードを記入ください - 開始
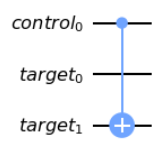
cu2.cx(c[0],t[1])
# コードを記入ください - 終了
cu2.draw('mpl')

実は１行書いたら終わりでした！超簡単ですね！

2-c

さあ、もうこれは同じ要領でやれば良いことはわかるので、これまでと同じように入力と出力のビットを見てみましょう。あれ？特に変わっていないですね。そうです、それで正しいのです！つまり、これは何もしないのと同じです。つまり何も書かなくて良いのです！ヒントにもあるように最適解はシンプルとあるので、確信が持てるかもしれません。

ex2c

c = QuantumRegister(1, 'control')
t = QuantumRegister(2, 'target')
cu4 = QuantumCircuit(c, t)
# コードを記入ください - 開始
# コードを記入ください - 終了
cu4.draw('mpl')

これらをまとめた問題

最後は用意されたコードを実行することで、これまでに作られたコードが自動的に追加されますので、そのまま実行します。

すると、コスト6の回路ができるので、これで正解をもらえます。

exercise2の補足

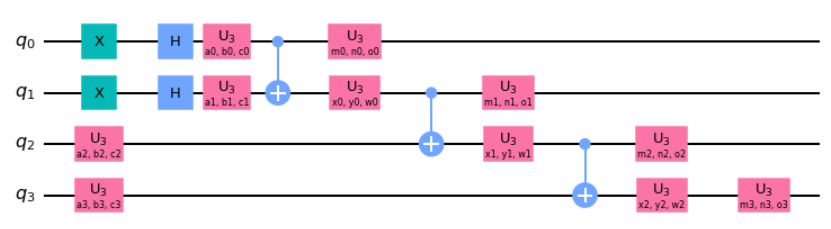
最後に出てきた回路ですが、これは何をやっているのかというと、量子位相推定の一部の回路を作っています。以下の赤枠の1～2の部分がそれに相当しています。なので、$U$、$U^{2}$、$U^{4}$の３つのゲートを埋め込んでいることになります。

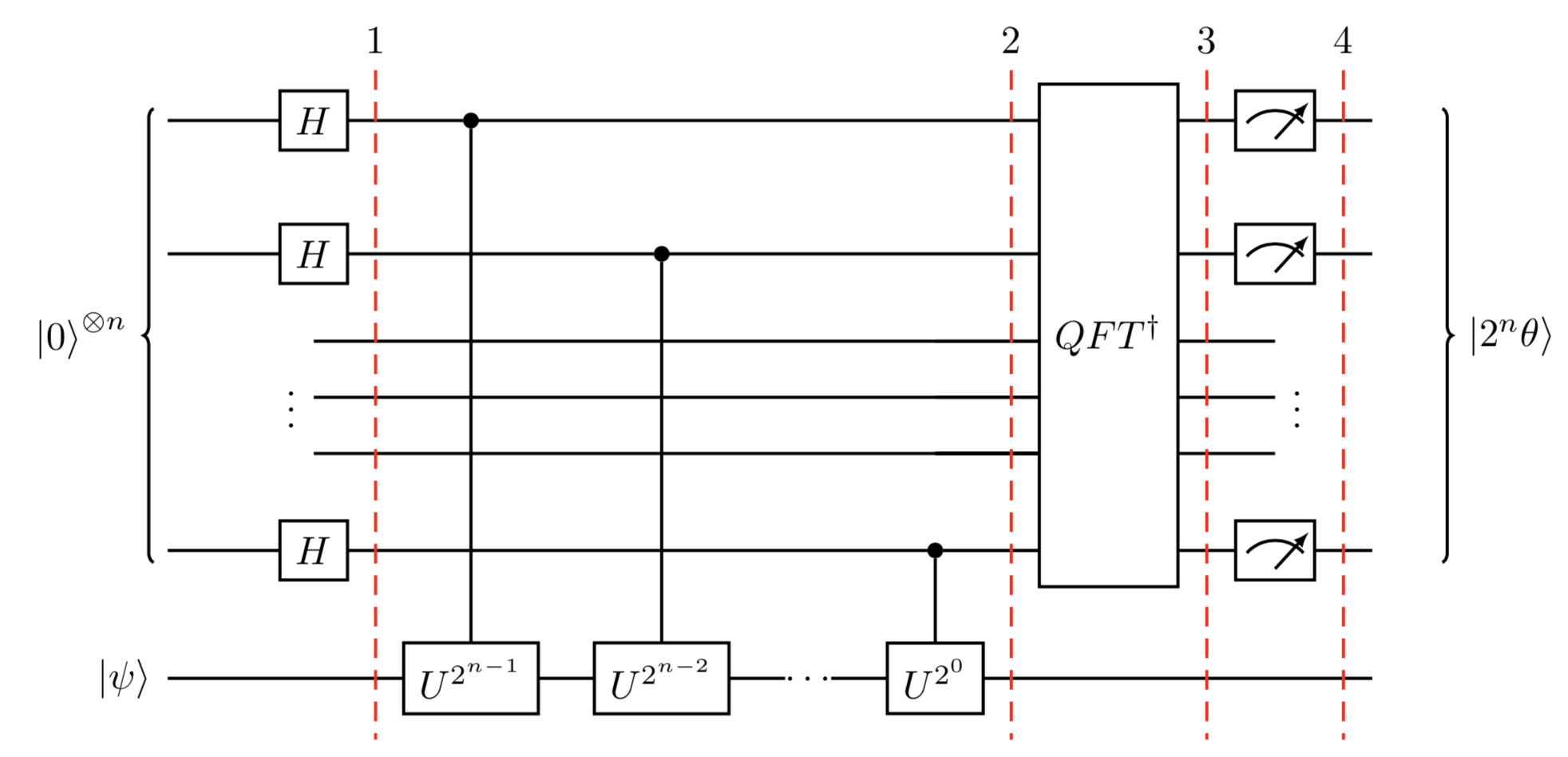
図と回答との対比が少しわかりにくいですが、$U^{4}=I$はなので、実際には特に何も書かれていません。また、一番下の$\ket{\psi}$も１量子ビットである必要はなく、複数量子ビットで構成された今回の回答のようなケースも考えられます。

exercise3（量子誤り訂正）

第３問は量子誤り訂正に関する問題です。量子誤り訂正とは、量子ビットに何らかのノイズが乗ってしまい本来のデータとは違う状態になったとしても、それを特定し修復する操作を含む手法になります。
今回はエラーの特定に焦点を当てています。

誤り訂正では、計算上のデータを保持する計算ビットと、エラーのその計算ビットに発生したエラーを検知するシンドロームビットの両方を使います。シンドロームビットにはどこの量子ビットにどのエラーが起こったかを値として保持できるようにする必要があります。前置きの解説ではそれを丁寧に説明しているので読んでみて、発想を理解してから取り掛かると良いでしょう。

余談ですが、本来の誤り訂正ではエラーを検知してから、それを復元する所まで構成する必要がありますが、ここではそこまで解説していませんし、そこまで実装することも要求されていません。

では問題を見てみましょう。

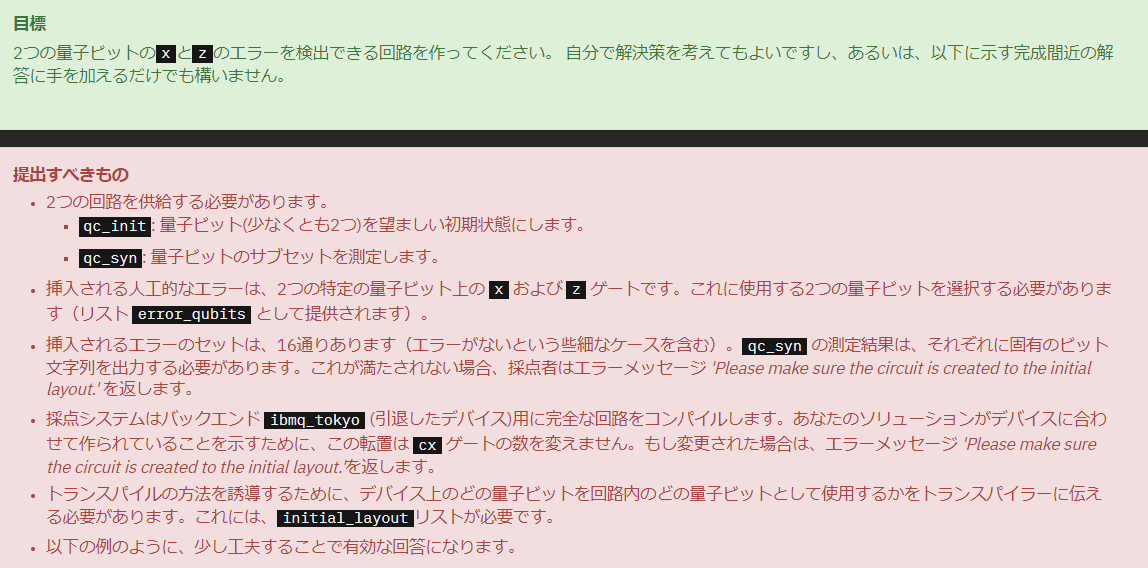
問題

今回の問題では、２種類のエラーXとZが発生して、量子状態にノイズが乗る設定になっています。また、「提出すべきもの」という箇所を読んでもらうと、エラーが発生する箇所は特定の２つの量子ビットに制限され、それを指定できます。もちろん本来であれば、エラーの種類はもっとありますし、全ての量子ビットに発生しうる可能性はありますが、今回はそこまで考えなくて良いということになります。
また注目すべき所として、**「あなたのソリューションがデバイスに合わせて作られていることを示すために、この転置は cx ゲートの数を変えません。」**という文言を気にする必要があります。これは実機で動かすときにデバイスの持つ制約を考慮して量子回路を構成せよというが課題になっていることを表しています。
どういうことか少し説明します。
今回はFakeTokyoと呼ばれる量子デバイスのシミュレーターを使います。notebookを実行すると途中でこんな絵が出てきます。

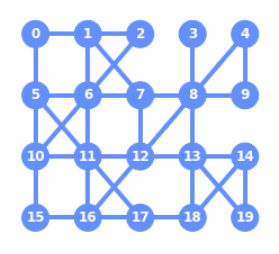
数字が書いてある〇は、量子ビットの番号を表しています。では、その丸の間にあったりなかったりする線は何を表しているのでしょうか？これは、各量子ビットが相互作用できるかどうかを示す線になります。「相互作用ができるかどうか」というのは「CXゲートを使って２つの量子ビットを操作できるか」ということを意味しています。つまり、線が繋がっている量子ビット間でしかCXゲートを使いことができないのです！実際のデバイスではこのような制約が存在しており、実機を動かす
場合にはこの構成の制約を考慮して量子回路を組まないと実機が動かせない場合があります。
シミュレーターだと意識しないことを実機ではそういった制約があるので注意が必要です。

解説

では、解説をしていきます。今回は表面符号と呼ばれる回路がサンプルとして書かれているので、これを使うことにしましょう！もちろん、好きに書いても良いですが、見通しが無い場合はこのサンプルを使うのが手っ取り早いです。

cが計算ビットで、sがシンドロームビットです。計算ビットとシンドロームビットが交互に並んでいる構成になっています。これにより計算ビットのエラーをシンドロームビットに相互作用させることで伝播できるので、シンドロームビットの状態からエラーが判断できるという寸法になっています。

この量子ビットの構成を実機の量子ビットにマッピングする設定が以下になっています。

initial_layout

initial_layout = [0,2,6,10,12,1,5,7,11]

左から、c0、c1、・・・s3という順番で指定していきます。そうすると、確かにFakeTokyoの左上の部分にマッピングされているのがお分かりいただけると思います。さて、ここで問題が出てきます。表面符号の構成を見ると、隣り合う量子ビット間では相互作用の線がありますが、FakeTokyoの２番と７番の量子ビットにはそのような繋がりが無いのです！
ここを上手く補完するように量子回路を組み替える必要がありそうです。（実際に、これがこの問題のポイントです）

実際にこの繋がりの有り無しを考慮しないで、表面符号の構成に沿って回路を組んでGraderに通すと「Please make sure the circuit is created to the initial layout.」というメッセージが返ってきます。これは、実機の構成に合わせようとして、繋がりの箇所のCXゲートを別の量子ビットにCXゲートを何回か通して結果の整合性が合うように、内部的に量子回路を組み替えるということを良きに計らってやってくれています。遠回りして値を伝播させているようなものなので、その結果としてCXゲートの数が増えてしまうということになります。今回の問題ではこれだと間違いとして扱われるので、内部的な組み換えがなくなるように量子回路を組みことと、レイアウトを合わせる必要があります。

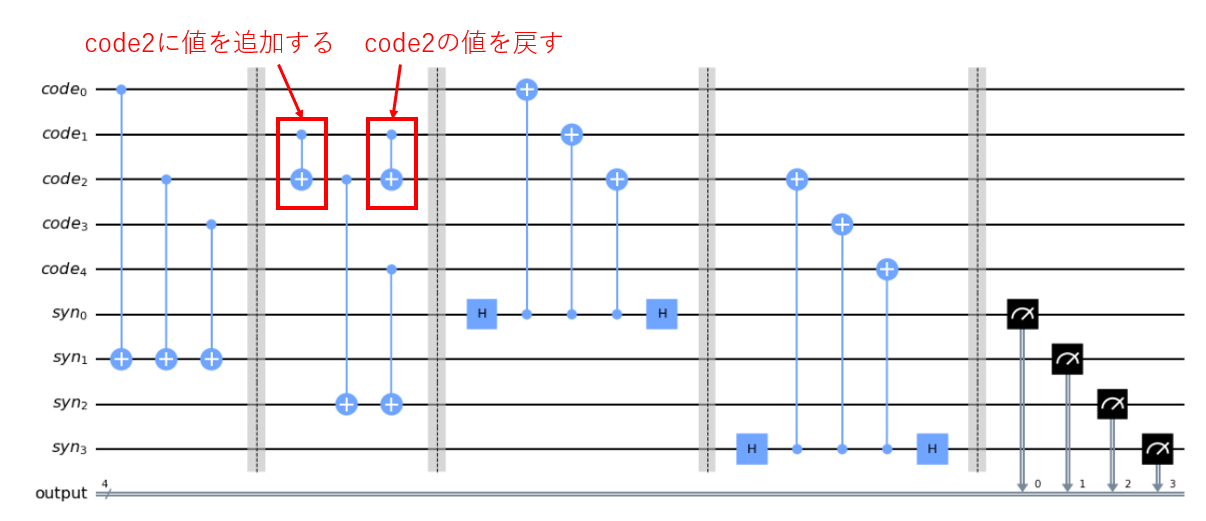
エラーの情報をシンドロームビットに伝える回路はこんな感じに書かれています。

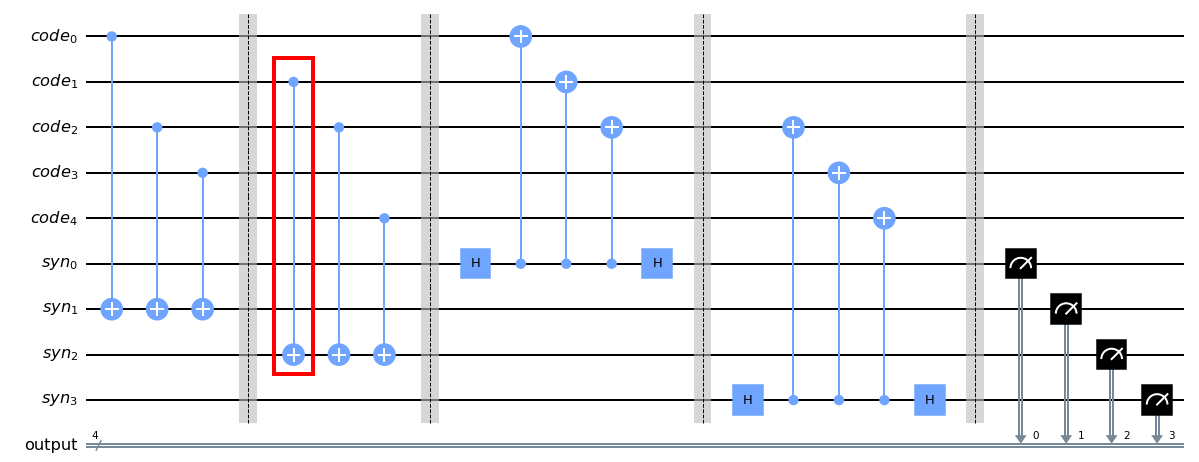
気にする箇所は赤枠で囲った番号２番の量子ビットに対応するcode1と番号7番に対応するsyn2のCXゲートです。FakeTokyoではここには直接CXゲートを通すことができません。
では、どうするかなのですが、着想としてcode1の値を一時的に別の量子ビットに移してそこから伝播させてもらうことです。となると、code1に繋がっている量子ビットを探す必要があります。FakeTokyoのトポロジーをもう一度眺めると、番号２番は番号６番（=code2）が繋がっていることがわかります。そして、code2からsyn2にCXゲートが通っているので、シンドロームビットに値を伝える前に、code2にcode1の値を追加すれば上手く行けそうです！
ただし１点だけ注意が必要なことがあります。code量子ビットは最初と最後で同じになるようしておく必要があります。これはエラーを検出するための回路ですから、code1からcode2に値を送り込んだ後は元に戻してあげる必要があります。
以上を踏まえると、以下のように回路を修正できます。

syndorom

qc_syn = QuantumCircuit(code,syn,out)


# Left ZZZ
qc_syn.cx(code[0],syn[1])
qc_syn.cx(code[2],syn[1])
qc_syn.cx(code[3],syn[1])
qc_syn.barrier()

# Right ZZZ
#qc_syn.cx(code[1],syn[2]) # CXゲートで直接通せないのでコメントアウト
qc_syn.cx(code[1],code[2]) # code1の値をcode2に送る
qc_syn.cx(code[2],syn[2])
qc_syn.cx(code[1],code[2]) # code2の値と元に戻す
qc_syn.cx(code[4],syn[2])
qc_syn.barrier()

# Top XXX
qc_syn.h(syn[0])
qc_syn.cx(syn[0],code[0])
qc_syn.cx(syn[0],code[1])
qc_syn.cx(syn[0],code[2])
qc_syn.h(syn[0])
qc_syn.barrier()

# Bottom XXX
qc_syn.h(syn[3])
qc_syn.cx(syn[3],code[2])
qc_syn.cx(syn[3],code[3])
qc_syn.cx(syn[3],code[4])
qc_syn.h(syn[3])
qc_syn.barrier()


# Measure the auxilliary qubits
qc_syn.measure(syn,out)
qc_syn.draw('mpl')

赤い箇所が修正箇所です。

これで最後まで通すと正解になりますし、最小の修正で済む回答になっています。
もちろん、これ以外の正解となる、表面符号のレイアウトと回路の組み合わせがあると思いますので、自由に考えてみてください！

exercise4（トランズモン量子ビット）

第４問は、量子コンピューターのハードウェアに関する問題です。ここではパルスを使って量子ビットを操作することを学びながら、実際に自分でゲートを作ります。
パルスとは、量子ビットの状態を操作する信号のことです。例えば、実際に重ね合わせ状態を作るHゲートだったり、ビットの値を反転させるXゲートはこのパルスを上手く作ることで実現しています。
前置きでは$\ket{0}$から$\ket{1}$という状態を作る操作を解説しています。この状態は量子物理的にはエネルギーの最も低い基底状態を$\ket{0}$として、エネルギーが２番目に低い状態を$\ket{1}$となるように作ろうとしています。このエネルギーが異なる状態に遷移させるにはイイ感じのパルスのパラメーターを探す必要があります。（量子物理の世界では状態の持つエネルギーは飛び飛び（離散的）になっていて、決まったエネルギー差があるので、それに合うようなパルスのパラメーターも決まっていることになります。）
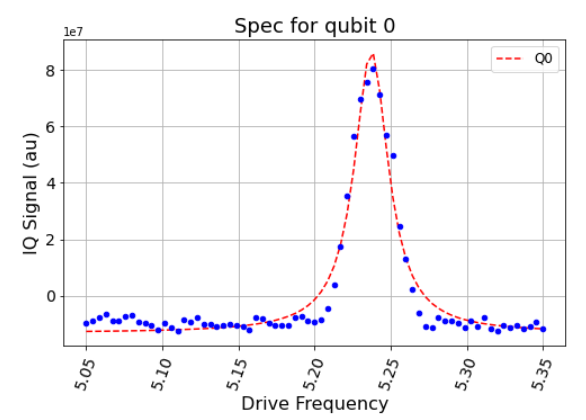
パルスを使って状態を遷移させることができるパルスの周波数を探すことができます。探すには怪しいと思われる周波数の周辺で細かく周波数を変えながら結果を見ます。すると、イイ感じに信号が増強される周波数が見つかります。後はそこに統計的なプロットを掛けて頂点になる箇所の周波数をXゲートを実現する周波数と見なすことができるというわけです。

問題

これを真面目に0から理解しようとするとかなり難しいので、基本的には前置きにかかれているコードを流用しましょう。そこに入れられるパラメーターを弄ることで回答を探します。
基本的にいじったパラメーターは、amp=driver_ampの箇所になります。これを増やしたり減らしたりして、イイ感じの所を探りました。今回はamp=drive_amp*1.5としたら正解が出てきました。
また、共鳴する周波数は$\ket{0}→\ket{1}$の箇所からは少しズレるので、それを補正するパラメーターとして周波数を探る領域をfreq+anharm_guess_GHzとすることで-300Mhzずらしています。

1to2pulse

# Define pi pulse
x_pulse = Gaussian(duration=drive_duration,
                     amp=x180_amp, 
                     sigma=drive_sigma,
                     name='x_pulse')

#print(spec_pulse)
def build_spec12_pulse_schedule(freq, anharm_guess_GHz):    
    with pulse.build(name="Spec Pulse at %.3f GHz" % (freq+anharm_guess_GHz)) as spec12_schedule:
        with pulse.align_sequential():              
            # こちらのコメント間にコードを記入ください - 開始
            excited_pulse = spec_pulse = Gaussian(duration=drive_duration, amp=drive_amp*1.5, sigma=drive_sigma, name=f"excited drive amplitude = {drive_amp}")
            pulse.play(x_pulse,DriveChannel(qubit))
            pulse.set_frequency((freq+anharm_guess_GHz)*GHz, DriveChannel(qubit))
            pulse.play((excited_pulse), DriveChannel(qubit))
            pulse.call(meas)         
    
            # こちらのコメント間にコードを記入ください  - 終了
    return spec12_schedule

最終的にはこんな感じにフィッテングできて 4.897228Ghzあたりに共鳴周波数が見つかるという結果になりました。

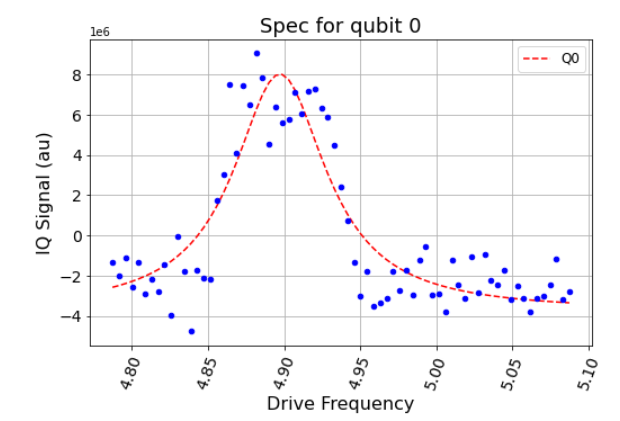
ここはパラメーターを弄ると、もう少しキレイなグラフができるかと思うので、いろいろパラメーターを探ってみてください！

exercise5（変分量子固有値ソルバー:VQE）

最後の問題は、量子化学計算で利用することが期待されるVQEに関する問題です。これが解けると、その時の回路のコストが最終スコアとして登録され、参加者はこのスコアを下げることで競争します。
前置きでは、水素分子（H2）の基底状態（エネルギーが最小の状態）をVQEを使って探る方法が解説されています。QiskitでVQEを動かすときには、調べたい分子の情報を入れると、それを量子回路で実行可能な形に置き換えてくれる関数が用意されているので、基本的にはそれを使って下準備をしてから解くことになります。

またこの水素分子については、量子化学の世界では最も簡単な問題になっています。それは登場する電子や電子軌道が最も少ないため、量子回路も小さく抑えることができるので現実的にCPUでもシミュレート可能なレベルになっています。しかし、それ以外の分子になると途端に問題サイズが大きくなり、必要な量子ビットもゲート数も増えていきます。そうなるとシミュレートも厳しくなります。それを意識した問題になっています。

ではVQEも量子化学もそんなに詳しくない人にそんなこと本当にできるの？という疑問が湧いてきそうですが、最初にこんなことが書いてあります。

こんなの見たら誰だってビビっちゃいますよね！著者もビビッてしまいましたｗ

ですが、課題を解く前には、じっくり水素原子でシミュレートの流れを押さえておくことをおススメします。

問題

LiH（水素化リチウム）の基底状態を求めるansatz（量子回路）を探る問題になります。水素化リチウムは水素分子の次に小さい分子となるので、それを実際に自力でやってみることになります。

この問題を解く上では、前置きに書かれている水素分子でのチュートリアルを順になぞる所から始めると良いでしょう。それを水素化リチウムの問題に当てはめていけば、いったん量子回路が組めます。ただ、コピペしたコードに何も手を入れずにやってみると上手くいきません。

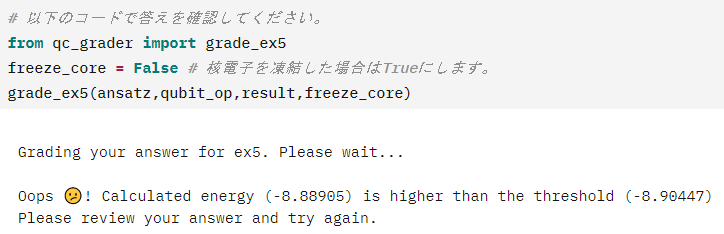
基底状態のエネルギーが理論値からある程度の誤差の範囲に収束していないようです。
そこで、いろいろ変更できそうなパラメーターや設定を弄りながら、試してみましょう。
なお、この問題を解く上では、多くのパラメーターがあり、それらの組み合わせを変えて試行を繰り返すことが最も重要です。

すぐに弄れそうなところで、ansatz_typeなるものを弄ってみることにします。デフォルトではansatz_type='TwoLocal'となっていますが、**例えば、ansatz_type='SUCCD'としてみると、先ほどよりもエネルギーが低い値に収束しました。**これは良さそうです。

これをGraderにかけてみます。すると・・・

CX（CNOT）を4032個も使っているとのことです。。。クリアするためにはCXを500個以下に減らさないといけないとのことです。他のansatz_typeも試してみても、そんなに違いはなさそうです。

実際にVQEを動かしていると、水素原子の時はサクサク動いていたと思いますが、水素化リチウムではモッサリ動いていると思います。これは水素分子と比べると問題サイズが大きくなり必要な量子ビットのが増えています。init_stateの回路を描画すると12量子ビットあることがわかります。（init_stateを描画したのは回路全体はサイズが大きすぎて描画できないため）

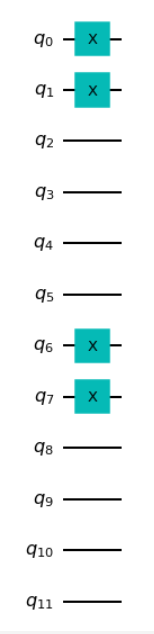
そうなると、ゲート数も増えますし、行列の積の計算量も増えているので当然と言えば当然です。なので、このままではダメです。

ここで一度、問題文に立ち返ってみます。するとこんなことが書いてあります。

ここからは、この文言に従って量子ビット数を減らす方法を探りながら進めていきます。

まずはクリアを目指す

量子ビットが12というのはシミュレートするにはサイズが大きいです。なので、このヒントに沿って問題サイズを小さくできるかやっていきます。これらがどういう意味を持つかはよくわからないと思いますが、モノは試しということでやってみましょう。
とっつき易い順に１つずつ試してみましょう。

量子ビット数削減のヒント1：two_qubit_reduction=TrueとParityMapperを使う

サンプルソースコードの中にmapper_typeとcoverterがあり、明らかに怪しいパラメーターがありますので、そこを弄ってみましょう。最初はこんな感じです。

before

mapper_type = 'JordanWignerMapper'
（途中省略）
converter = QubitConverter(mapper=mapper, two_qubit_reduction=False)

こんな感じにしてみます。

after

mapper_type = 'ParityMapper'
（途中省略）
converter = QubitConverter(mapper=mapper, two_qubit_reduction=True)

実際にこれでVQEを動かすと、さっきよりはサクサク動いていると思います。
回路のサイズを見てみましょう。init_stateを描画します。

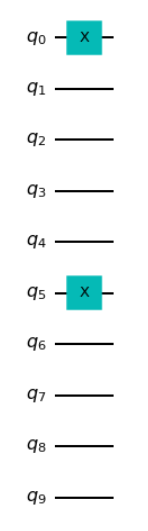
すると量子ビットが10個に削減できていることがわかります！two_qubit_reductionというパラメーター名通りですね！これはイイ感じです！
早速Graderにかけてみましょう！

まだ量子回路が全然大きいみたいですorz
残りのヒントは２つあるので次のを試してみましょう。ParityMapperを使いつつ、two_qubit_reduction=Trueは維持したままにします。

量子ビット数削減のヒント2：フローズンコア近似を試す

ヒントに従いAPI referenceを眺めているとqiskit_nature.transformersのページに行きつきます。

ただこれだけだと、どう使うかよくわかりません。。。
いろいろ調べたり、slack上の専用チャンネルでヒントを提示してくれている人がいるのでそれを参考にすると、ElectronicStructureProblemクラスの引数にq_molecule_transformersという引数があるので、これに入れることができそうです。

ちょっと試行錯誤した結果、こんな感じに使えるようです。（引数は配列にして、そこにオブジェクトを入れる必要があるようです）

from qiskit_nature.transformers import FreezeCoreTransformer
problem = ElectronicStructureProblem(driver,q_molecule_transformers=[FreezeCoreTransformer()])

さっきよりもメチャメチャ速くなりました！問題サイズも8量子ビットまで削除できています！

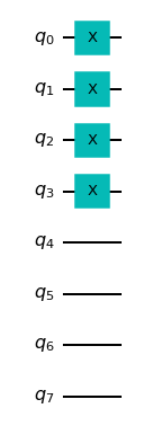
早速Graderにかけてみましょう！ここで注意が１つあります。フローズンコア近似を使った場合は、freeze_coreをFalseからTrueに変更しておく必要があります。TrueかFalseかで正解の基準とするエネルギーの値が全然違うの変更しておかないといつまで経っても上手くいきません。こんな感じです。

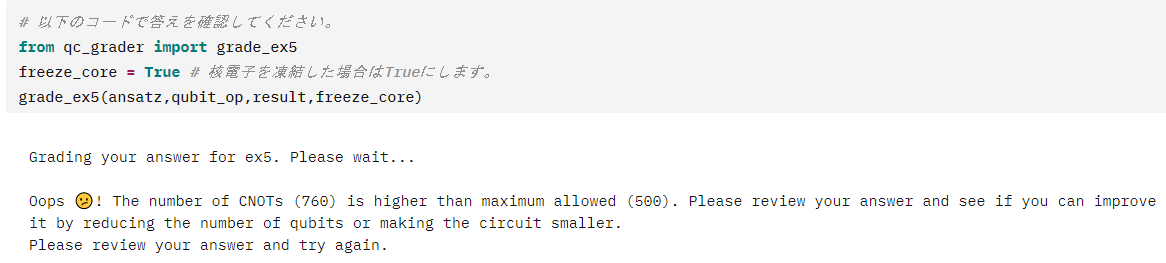
CXが760個まで削減できました！ansatzの描画はできるレベルまでにはなっているようです。先頭の所だけ抜粋してみます。

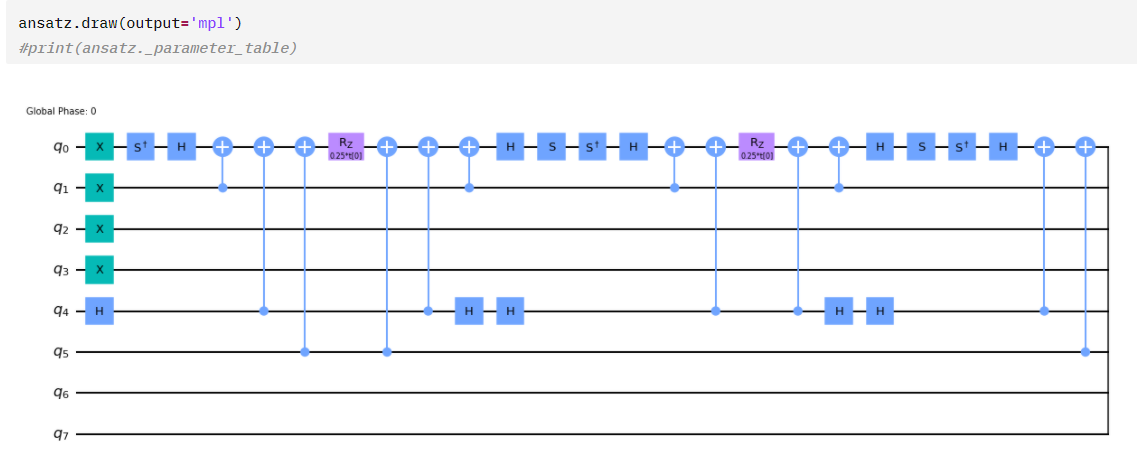
ただ、まだクリアには至りません。３つめのヒントを実行してみることにします。

量子ビット数削減のヒント3：Z2symmetriesを使う

z2symmetriesをググって調べてみますが、使い方に関する情報が出てきません。下手すると、古いバージョンの使い方のようなミスリードするような記事が見つかったりします。。。slack上のヒントを眺めます。すると、QubitConveterクラスの引数にそれらしきものがあるとのことです。確かにz2symmetries_reductionという引数があります。これっぽいですね。ただ使い方がパッ見とわかりません。。。困りました。ヒントに頼りましょう。
**どうやら配列に1か-1を入れたものを入れるとのことです。**よくわからないので、まずは適当に入れてみます。z2symmerties_reduction=[1]として実行してみましたがエラーになりました。どうやら２つ値を入れよとのことです。

以下のよう[1,1]を試しに入れてみます。

converter = QubitConverter(mapper=mapper, two_qubit_reduction=True,z2symmetry_reduction=[1,1])

お！動きました！は、速い！！！！これは期待できます。問題サイズはどうなっているでしょうか。

6量子ビットまでサイズが小さくなっています！これならかなりのゲート数を削減できている気がします！ワクワクしながらGraderにかけます！

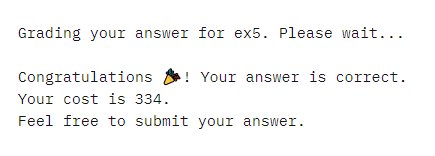
やった！やりました！！！！コストは334まで削減できています！これでクリアです！これで安心して、ぐっすり眠れそうです！

さらにコストを削減するという魔境に突入

さて、クリアして一安心ですが、回答を見るとコストが一桁台で提出されているものがあるようです。。。マジか・・・。（実はここからが魔境でした。）
とりあえず、ヒントに従い量子ビット数は削減できました。今度はもう一度anstatz_typeも変えたり、時にはoptimizerも変えたりして、収束性が遅い場合はイテレーション回数も増やしたりしました。どれだけ試行したかは覚えていません。気が遠くなるぐらいいろいろ試しましたｗ
（あんまり眠ってませんｗ）

いろいろやっている内に、著者は一度コスト20まで到達しています。（その時の回路が再現できず・・・）
ふと、そこからあることに気づきます。**「まだCustomの回路を試していないじゃないか。」**と。
ただ、Custom以外は過去の知見から自動でそれらしい回路を組んでくれるものですが、Customは自分で回路を組む必要があります。

着想としては、6量子ビットがそれぞれどこかの量子ビットと１度は相互作用（CXゲートを通す）させることやそれぞれの量子ビットに1量子回転ゲートを組み込むことです。それを必要最小限まで減らしてみます。やっていてわかったのですが、１つでもCXゲートがかかっていない量子ビットがあると上手く収束しません。
すると、そんな中コスト5の回路で収束するものが見つかりました！
一例としてこんな回路です。

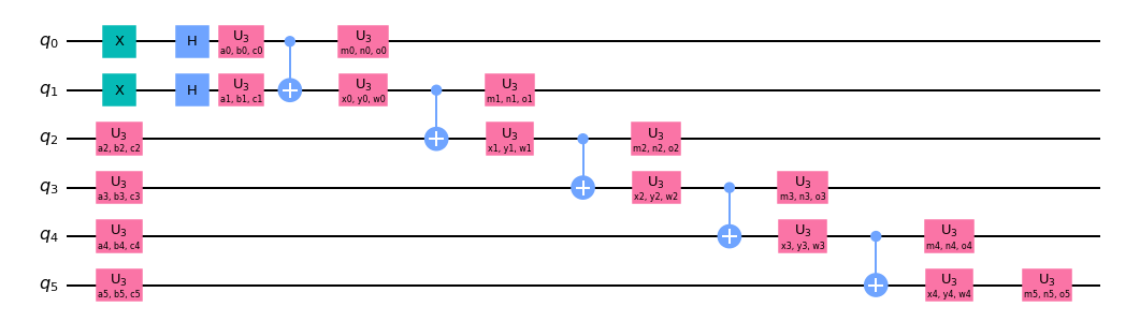
この時点で、公式の最少スコアとして3が最小であることが参加者に通知されました。（コスト1が一時点で最小スコアでしたが、それは適切でない回路だったため無効になっていました。）ではもうひと踏ん張りコスト3を目指してCXゲートを減らすことを試みます。
ですが、コスト5の回路からCXゲートを１つでも減らすと上手く収束しません。。。100回ぐらいいろいろ試してみましたが、何をやってもダメです。
困りました、、、、そこで一度発想を転換しました。

そもそも論として、**水素化リチウムの基底状態とはどうあるべきなのか？ということです。量子化学的な思想に立つと、４つの電子があり、それらのエネルギー軌道が低い所から埋まるのでは？ということでした。そうすると、エネルギー軌道として基底状態には使われていないのに余分な量子ビットが残っているのでは？ということを想像しました。その発想を元にエネルギー軌道を減らせるものがないかと色々調べていくと、FreezeCoreTransformクラスの引数にremove_orbitalsという引数があるではないです！！！これを見た瞬間「(ﾟ∀ﾟ)ｷﾀｺﾚ!!！！！！」**となったのを思い出しますｗ

使い方はよくわからないですが、おそらくエネルギー軌道の番号みたいなものがあるので、外側（エネルギー準位が高い起動）を除くことを考えて適当に数字を埋めてみて試行錯誤します。すると、これで量子ビットを減らせそうであることがわかってきました。（物理的な意味はよくわかっていない）

problem = ElectronicStructureProblem(driver,q_molecule_transformers=[FreezeCoreTransformer(True,[3,4])])

量子ビット数が4になっている！！！

これで確信しました。後は必要最小限のゲートを配置して、微調整していきます。そして、やっとコスト3に到達しました！（１度コスト4を経由して）

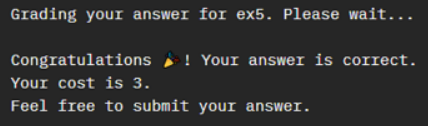
著者の最終回答

試行錯誤に錯誤を重ねまくった結果、これが一番少ないゲート数で正解が出せる所まで到達しました。
CNOTが3つでなので、コストが3となり、これが想定されていた最もコストが小さい回答の１つになっています。到達してみると、本当に必要最小限のゲートだけで構成できることがわかりました。ここまで簡単になるとは・・・・。

ここでの学びとしては、以下ですね。今後に活かしていきたいと思います。
・問題サイズはとにかく小さくしましょう
・必要なゲートだけに絞っていきましょう（試行錯誤が必要）
・API referenceはよく読みましょう
・問題はシンプルに考えましょう

実は・・・

Qiskit Tutorialに今回の最小コストの答えが載っていました。。。。
https://qiskit.org/documentation/nature/tutorials/07_leveraging_qiskit_runtime.html

これを見つけた人はいたのかもしれませんが、多くの人は見つけられなかったようです。著者と同じように試行錯誤をしたと思われます。（実際に到達したことをslackに報告したら、何人からか「ヒントをくれ」というDMをもらいました。もちろん答えは教えないで発想を提示しました）

著者が提出した回路とは違いますが、よく見ていると発想は同じです。必要最小限の1量子ビット回転とCXゲートでの量子ビット間の相互作用です。この答えを見たときに、ノーヒントでこの着想に至れたことは大変自信になりました。

#まとめ
いかがだったでしょうか？
今回の問題はハードウェアや、実際の具体的で実用的なユースケースを想定した問題が多く出題されました。過去の問題はアルゴリズム的な問題が多く、プロコン的な課題に対して、量子回路をどう組むかに焦点を当てていました。今回はどうQiskitを使うかに焦点を当てていたようです。どちらも大切な内容ではあるので、過去問含めて解いてみると、量子コンピューターないしはQiskitの理解が深まることでしょう。今後も開催されることもあるはずなので、是非皆さんもチャレンジしてみてください！

参考（過去のIBM Quantum Challenge）

IBM Quantum Challenge 2019
IBM Qunatum Challenge may4
IBM Quantum Challenge 2020