教師あり学習 "分類"
今回も元気よく、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていきますよ！
前回は、教師あり学習の"回帰"について説明したので、
第三回では、同じく教師あり学習の"分類"について書きたいと覆います！！
⚠︎※※注意※※⚠︎
・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。
・また、ネットで調べたレベルの知識がほとんどなので、
"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
その場合は非常に申し訳ないです。指摘していただけると幸いです！
前回までの記事
分類
"回帰"が"数値の予測"であったのに対し、
"分類"は"所属するラベルの予測"です。
よく知られている例だと、
新しく届いたメールが、迷惑メールかどうかを判断する"スパムフィルタ"や、
画像に何が写っているかを判別する"画像認識"などがあります。
"分類"も、"回帰"と同様教師あり学習であるため、正解となるデータを人間が定める必要があります。
"スパムフィルタ"では、大量のメールに対して、
"迷惑メール"、"迷惑メールではない普通のメール"という二つのラベルを定めてあげ、
そのデータを教師データとして学習を行い"分類器"を作ることで、新しくメールが届いた時に、
それが迷惑メールであるかどうかを判別することができます。
"分類器"の作成のアルゴリズムは多く存在します。
"スパムフィルタ"にはナイーブベイズという手法が使われていたり、
"画像認識"では今話題のディープラーニングという手法が、
ディープラーニングはそもそもニューラルネットワークと呼ばれるアルゴリズムが元となっている手法です。
その他にも、RandomForest・SVM・ロジスティック回帰・SCWなど、
たくさんの種類があります。
実際になんらかの"分類"を行う時は、データの特徴からアルゴリズムを絞り、
いくつか試した上で最適な手法を模索していくことのが一般的かと思います。
分類に関する用語
"分類"自体の説明はあらかた終わってしまいましたが、
少し短いので、"分類"においてよく使われる用語の説明をしたいと思います！
説明変数と目的変数
回帰の時にも出てきましたね。
スパムメールorスパムでないメール、のように求めたい変数のことを目的変数、
メールの本文のテキスト情報など、目的変数を求めるのに必要な変数を説明変数と言います。
二項分類と多項分類
その名の通りですが、
「AorAでない」のように、目的変数が二種類のものを二項分類、
三種類以上のものを多項分類と呼びます。
その他にも二値分類や、多クラス分類、などのように呼び方は色々あります。
呼び分けるのには理由があり、
どちらかにおいて特に有効な分類の手法があったり、
分類器の良し悪しを測る指標なども、違ったりします。
Confusion Matrix
日本語で"混同行列"です。
分類器で評価用のデータを分類してみた時に、
正解した数、間違った数を集計して表にしたものです。
正解のクラスと、予測されたクラスが行列で表されます。
二項分類の用語
「AorAでない」という分類をした時、
その評価に使われる値と用語です。
真陽性(TP: TruePositive)・・Aと予測してA
偽陽性(FP: FalsePositive)・・Aと予測してAでない
真陰性(TN: TrueNegative)・・Aでないと予測してAでない
偽陰性(FN: FalseNegative)・・Aでないと予測してA
正答率(Accuracy)・・予測に対してどれだけあっていたか
適合率(Presision)・・Aと予測したもののうち、実際にAであるものの割合
再現率(Recall)・・実際にAであるもののうち、予測もAであるものの割合
F値(F-measure)・・適合率と再現率のトレードオフに対してそのバランスを見る値
正答率 ＝ (82+91)/(82+18+9+91) ＝ 0.865
適合率 ＝ 82 / (82+9) ≒ 0.901
再現率 ＝ 82 / (82+18) ＝ 0.82
F値 ＝ (2*0.901*0.82) / (0.901+0.82) ≒ 0.859
基本的な分類では、正しく分類できているかどうかが大事なので、
正答率であるAccuracyを見ることが多いです。
ですが例えば、
「ガンであるかどうかの検査」など、
そもそもガンでない人に比べてガンの人が少ないので、
全員を"ガンでない"と判定しても、正答率はかなり高くなります。
また、ガンでない人をガンと判断してしまっても、
精密検査をするなり、経過を見ていく中でわかることですし、
まだ問題はありません。
ですが、実際にガンの人を"ガンではない"と判断してしまっては、
そのあとに適切な治療や検査を受けることが出来なくなってしまうわけですので、
非常に大きな問題です。
つまり、「ガン検査」においては、
正答率と適合率はあまり意味をなさない指標で、
再現率こそが最も大事な指標であることがわかります。
このように、目的に応じて適切な指標から、
分類器の良し悪し判断することが大切です。
多項分類での用語
基本的に使う指標としては二項分類の時とさほど変わりはないですが、
全体として捉えるか、目的変数の各項目毎に捉えるかという概念が出てきます。
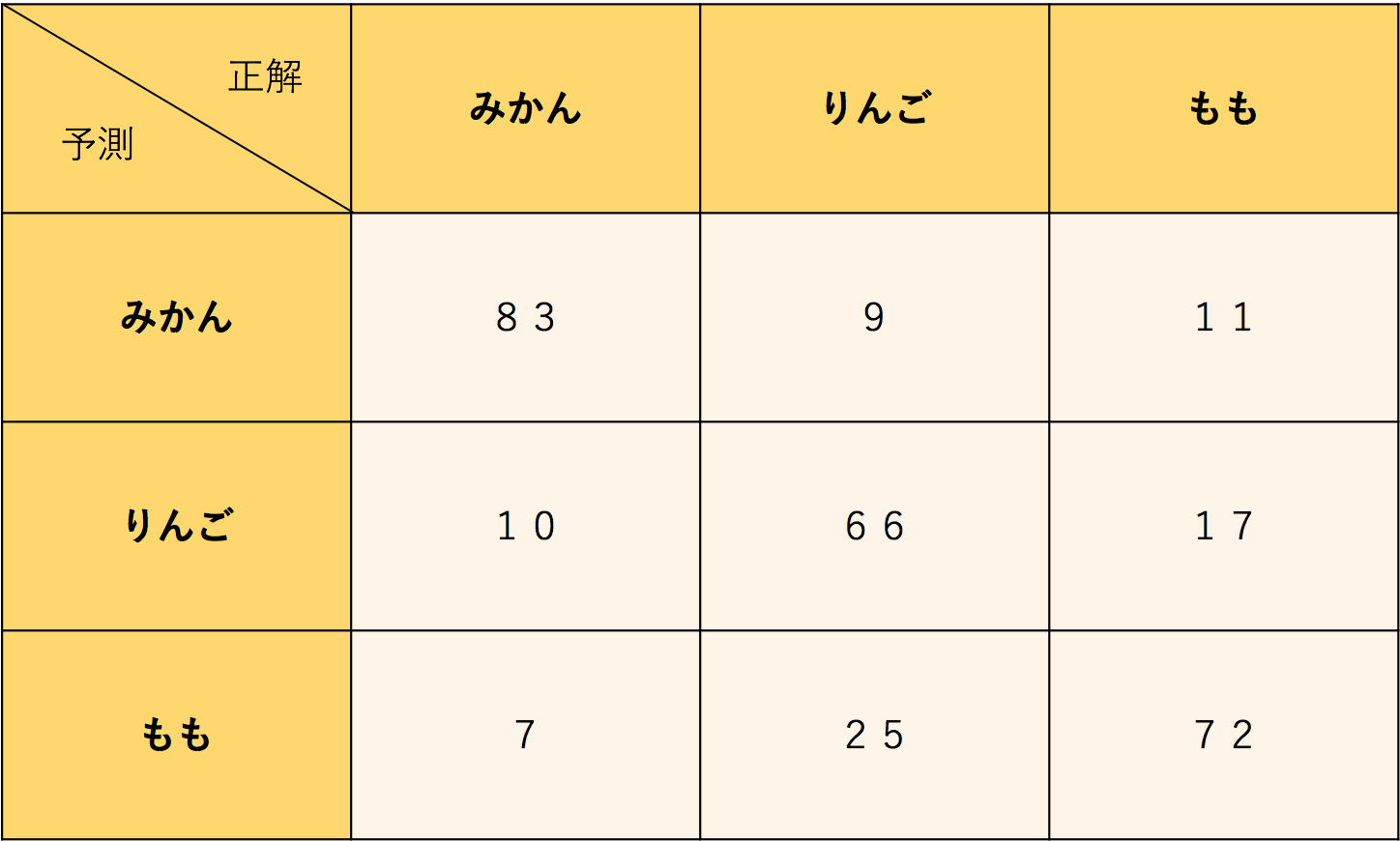
このConfusion Matrixは、各項目視点でみると以下のように分けることができます。
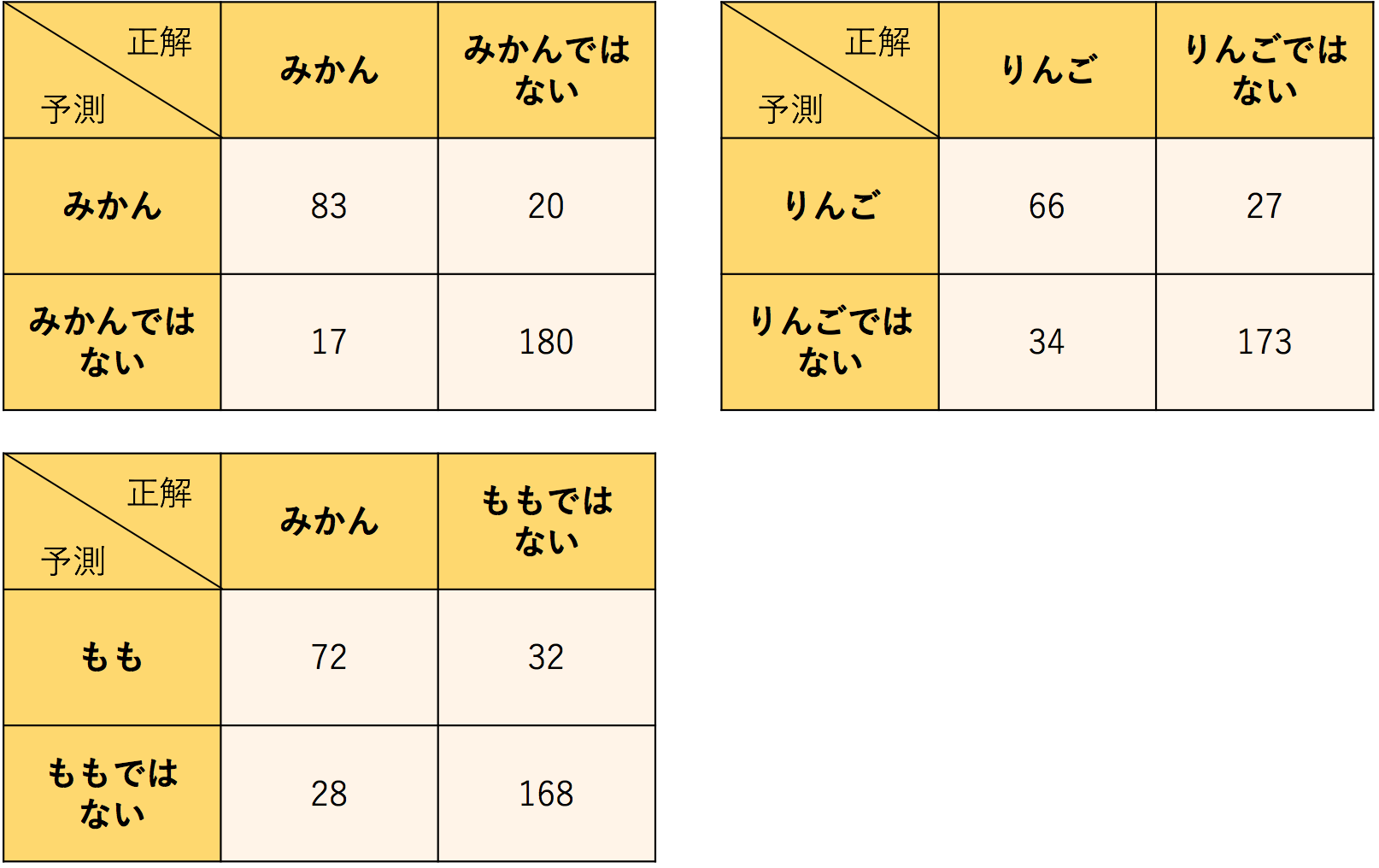
この時、
1つのセル単位に注目する（全体として捉える）microと
1つの表単位に注目する（各項目毎に捉える）macroという考え方ができます。
また、正答率も
全体の正答率である、overall accuracyと、
各項目の正答率の平均である、average accuracyに分けて考えられます。
average accuracyは小さな母数の項目の正確さも同等に評価します。
まとめ
・"分類"とは"所属するラベルの予測"をすること。
・目的変数が二値の分類を"二項分類"、三値以上の分類を"多項分類"と言う。
・分類器の良し悪しは、"正答率"・"適合率"・"再現率"・"F値"などを用いて評価する。
どの値を一番の指標にするかは、分類したい事象によって変わる。
・多項分類では、全体としての値は、各項目毎の平均か、というmicroとmacroの視点で評価をする。
あとがき
駆け足で用語の説明となってしまいましたが、いかがだったでしょうか？？
分類器の良し悪しを測る指標として、今回は基本的なものを解説しましたが、
他にも色々な指標が存在します。
（僕の理解が完全でないというのもあり、）それらはまた別の機会に書こうと思います。
次は、分類の手法の一つである、"Random Forest"について、
どのように分類を行うか具体的に説明したいと思います！
ここまで読んでいただき、ありがとうございました！！