教師あり学習 〜回帰〜

さて今回も、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていきます！

前回の記事では、機械学習の概要について大雑把に書いていきましたが、

第二回ではその中の手法の一つ、教師あり学習の"回帰"について、
焦点を当てて説明をしていきたいと思います！

⚠︎※※注意※※⚠︎

・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
　そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。

・また、ネットで調べたレベルの知識がほとんどなので、
　"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
　その場合は非常に申し訳ないです。指摘していただけると幸いです！

回帰

"回帰"とは簡単に言うと、"数値を予測すること"です。

例えば、「明日の気温は何度？」だったり、
「今月の売り上げはいくら？」などを予測することをイメージすると、分かりやすいかと思います。

明日の気温を予測する時は、ここ一ヶ月の気温や去年の同じ時期の気温など、「過去のデータ」を使って予測することになると思います。
また、気温の話ではイメージしにくいですが、「現在のデータ」を使って「過去のデータ」を予測することもあるかもしれません。

そのように、"知っている数値から知らない数値を予測する"というのが、"回帰"の概念です。

身長と体重

まだ分かりにくいと思うので、もう少し具体的に、
"身長から体重を予測する"ことを例に説明していきたいと思います。

今、以下のような身長のデータがあったとします。

身長	体重
150.6cm	48.7kg
150.7cm	53.3kg
:	:
169.3cm	63.2kg
169.9cm	67.1kg

このデータから、例えば「身長180cmの人ってどれくらいの体重なんだろう？」
というのを予測してみます。

まずはこのデータを、散布図にしてみます。

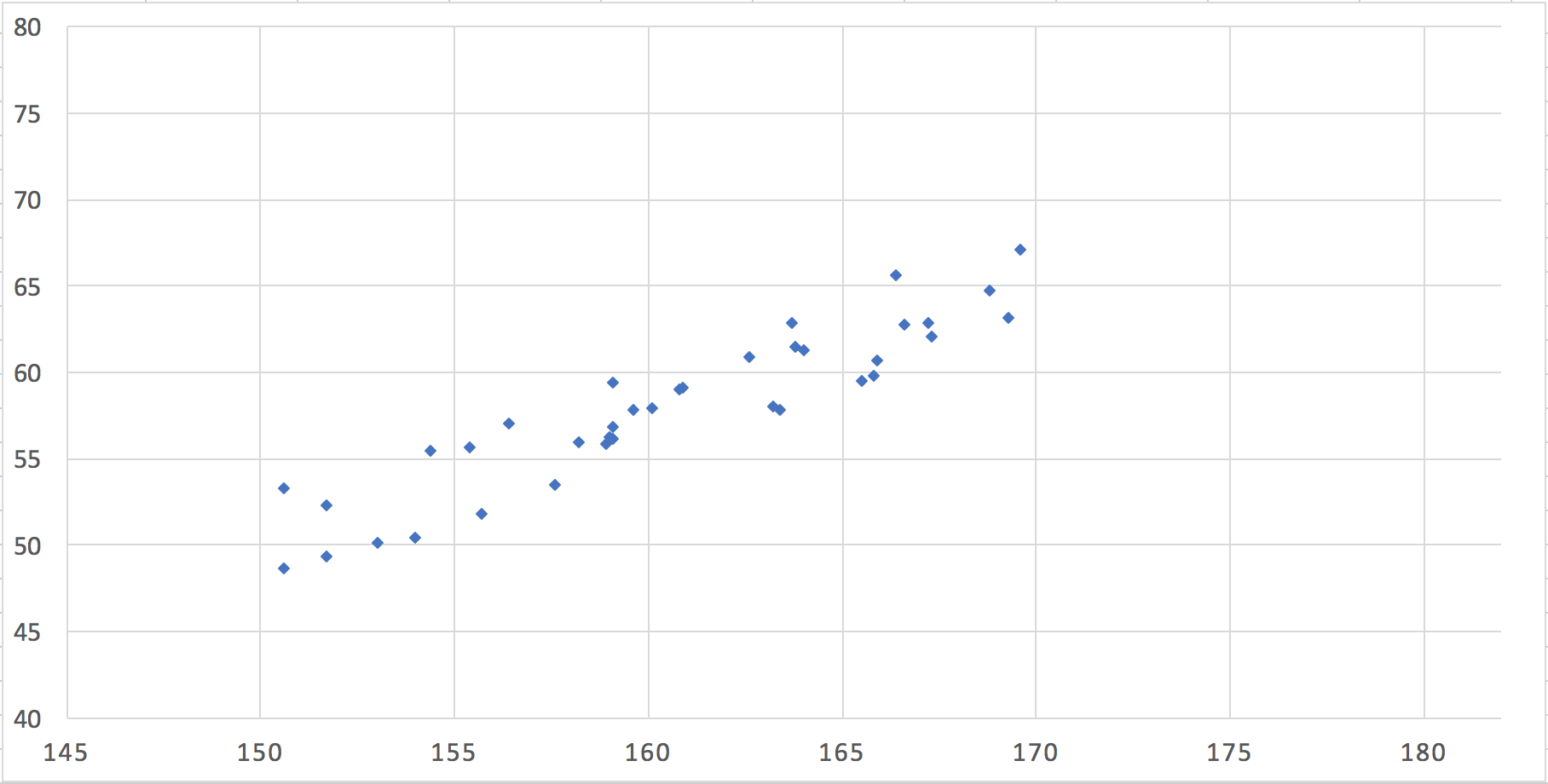
"回帰"とは、色々な手法がありますが、
つまるところ、"この図に対して、身長と体重の関係を表す線を引くこと"です。

今、"最小二乗法"という手法を用いて、直線を引いてみると、

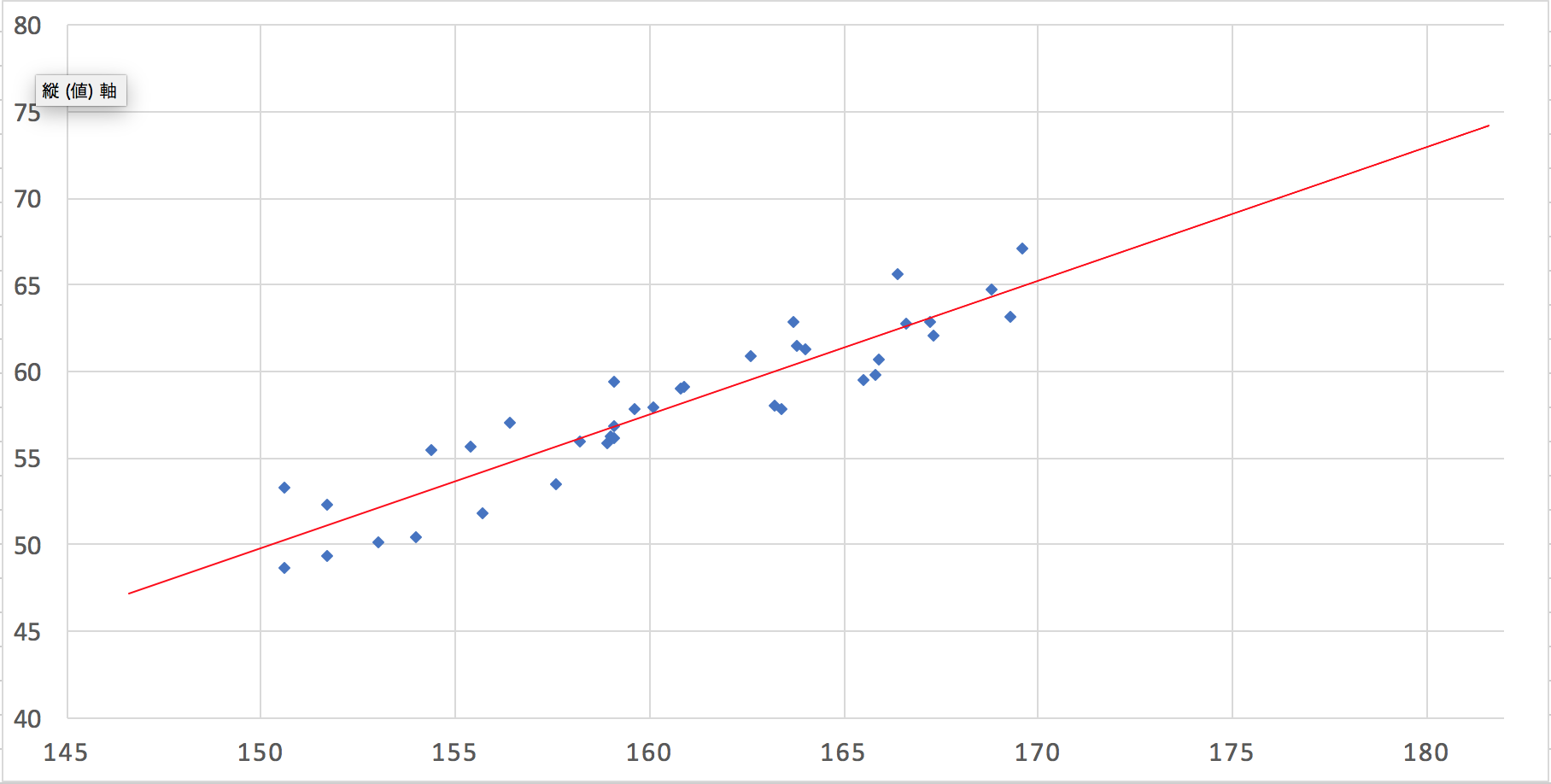
図ようになります。
この時、「180cmの人の体重」は大体　73kgぐらいかなと予測できるわけです。

これが、"回帰"を使った予測です。

線形と非線形

先ほどの例ではデータに対して、y = ax + b となるような"直線"をひきましたが、
もしかしたら二次式や三次式のほうが、データを上手く表現できたかもしれません。

先ほどのように、直線で回帰することを「線形回帰」、
直線以外のなめらかな線で回帰することを「非線形回帰」と言います。

どちらのほうが優れた回帰の手法というわけではなく、
データにあった回帰の仕方を模索するのが、"回帰"の醍醐味です。

単回帰と重回帰

「身長と体重」の例では、"身長"という一つの変数だけから、
目的の変数である"体重"を予測していました。

ですが、実際に体重を予測しようと思うとき、"身長"だけではなく、
"胸囲"や"直前の食事の量"などといったデータを使用することができると、より精度の高い回帰が行えると思います。

体重　＝　a * 身長 + b * 胸囲 + c * 食事量

このように、複数の変数から回帰を行うことを"重回帰"、
一つの変数から回帰を行うことを"単回帰"と言います。

データ分析の現場では、複雑な要素が絡み合うものを予測する必要があるため、
重回帰を使って分析をすることが多くなると思います。

ちなみに、今回の例で言う"体重"のような、求めたい変数のことを"目的変数"、
逆に目的変数を求めるために使う、"身長""などの変数のことを"説明変数"と言います。

まとめ

・"回帰"とは、"数値を予測する"こと。つまり、"データの関係性を表す線を引く"ことである。

・直線で回帰を行う"線形回帰"と、直線以外のなめらかな線で回帰を行う"非線形回帰"が存在する。

・目的となる変数に対して、一変数から予測することを"単回帰"、複数の変数から予測することを"重回帰"と言う。

・求めたい変数を"目的変数"、そのために使う変数を"説明変数"と言う。

あとがき

第二回、いかがだったでしょうか？

分かりやすく、長くなりすぎないことを意識すると、
どこで切るか、どこまで踏み込んだ説明をするか難しいですね。。

一旦数式などはおいておき、概念というか雰囲気だけでも掴んでもらえたら幸いです。
将来的には数式の説明や、R・pythonなどでどうやって行うか書けたらいいなぁ・・

次回は"教師あり学習"のもう一つの要素"分類"に関して記事を書きます！

ここまで読んでいただき、ありがとうございました！！