はじめに
テトロミノ敷き詰め問題を量子コンピュータ(シミュレータ)で解いてみます。前回3つの正方形でできたピースの問題を解いてみましたが、今回は4つです。ちなみに、3つのはトロミノと言うそうです。
「ペントミノ「のような」タイル敷き詰め問題を量子コンピュータで解いてみる」
https://qiita.com/drafts/5ddb63f74193babf9b7e/edit
問題
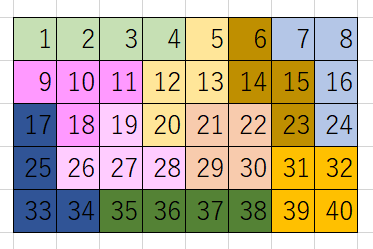
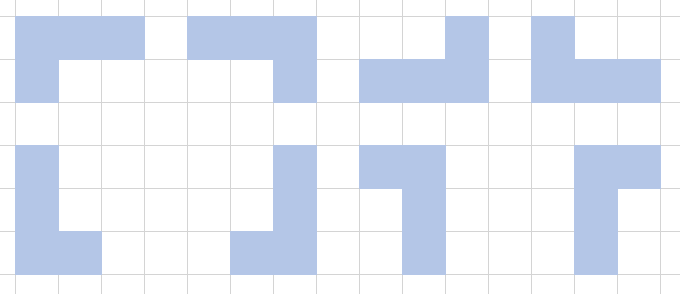
テトロミノとは、4つの正方形を組み合わせた形状のことで、下図の5つのピースがあります。テトリスと同じです。ピースは、回転したり、裏返したりすることができます。

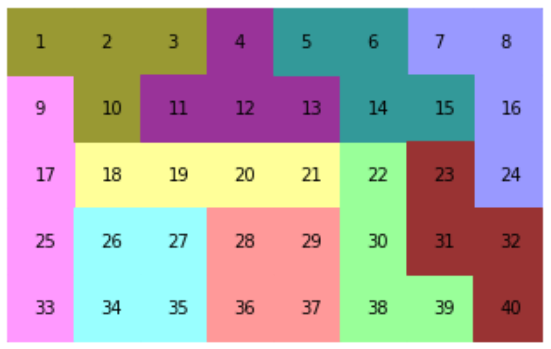
このピース2つずつを、下図のようにボートに敷き詰めていきます。
考え方
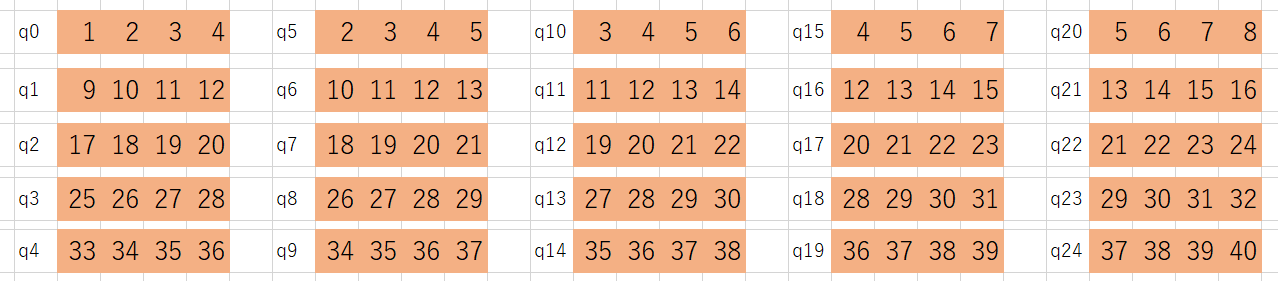
3つの時と同じように、まずは、ピースp0の盤面への置き方を考えてみます。下図のように41通りあるようです。この置き方を、それぞれ「q0, q1, q2, q3, q4, q5・・・」とします。
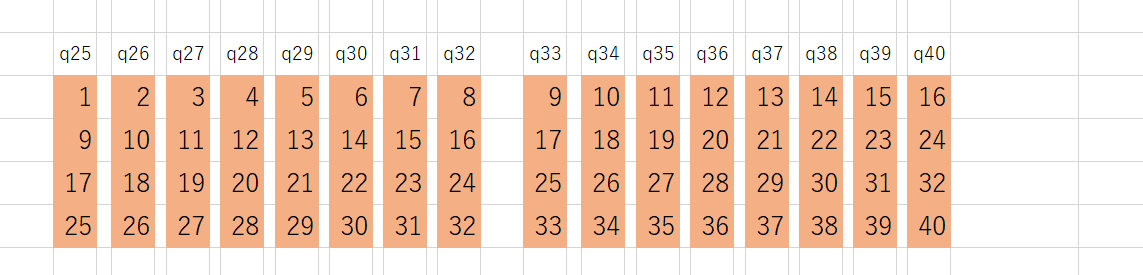
他のピースについても置き方をすべて考えて、それぞれq41, q42・・・と割り当てます。ピースによっては下図のように回転・反転で8通りありますので、8通り×それぞれの置き方を考えます。
今回は3つ(トロミノ)の時と違って、人力ですべて書き出すことはできないので、この書き出しもPythonでやります。例えば、私はそれぞれのピースを以下のような行列で定義して、numpyの回転と反転と掛け算を使って作りました。
p = [[[1,1,1,1]],
[[1,1],[1,1]],
[[1,1,1],[1,0,0]],
[[1,1,1],[0,1,0]],
[[1,1,0],[0,1,1]]]
本当は、対称性や置いちゃダメな置き方(端が1つだけ空いてしまうなど)もあるのですが、とりあえず全部列挙してしまいます。すべてのピースのすべての置き方を列挙すると429個ありました。
立式
立式も3つの時とほぼ同じです。イジングモデルやQAOAで解けるように立式してみます。
量子ビットが表すものを決める
ピースp0は、q0~q40のどれかの置き方になるはずですので、置き方q0になるときに、q0=1 、q0にならない時 q0=0 とします。同様にして、q1になるとき、q1=1, ならないときq1=0・・・、ピースp1についても、置き方q41になるときq41=1, ならないときq41=0・・・とします。
各ピースについて、置き方の中から2つだけ選ばれるようにする・・・①
まずは、p0の置き方は「q0, q1, q2, ・・・, q40」の41個がありますが、その中から同じ形のピース2つ分が選ばれるようにします。
41個の量子ビットの中から2つだけが選ばれる、という条件を最小値問題の式にしてみます。以下のようになります。
\{2-(q0+q2+q3....+q40)\}^2
これで、q0~q41の中で、2個だけ1のとき最小値の0、それ以外は1以上の値になります。
同様にして、ピースp1, p2・・・についても立式していきます。
盤面の各位置(1, 2, 3・・・)に置くピースが重ならないようにする・・・②
次に、盤面に注目します。
盤面の「1」の位置に置かれる可能性のあるピースは1つだけ選ばれるようにします。ピースは重なってもだめだし、どれか1つは配置されていないとダメなので、盤面の「1」上に来る可能性のあるピースの中から、1つだけを選ぶ必要があります。先ほどと同様に立式すると、
\{1-(q0+q25+q41+q69+...)\}^2
とすれば、盤面の位置1に置かれるピースの配置が1つのみに絞られます。q0, q25はピースp0の置き方の中に含まれています。q41, q69・・・はp1, p2・・・の置き方です。
盤面の他の位置2, 3, 4, 5・・・についても同様に立式します。
QUBO作成
イジングモデルやQAOAで解けるようにQUBOの形にします。
式が長くて展開に時間がかかるので、今回はQUBOに直接値を入れて作成しました。条件①のQUBOは以下のような感じです。
[[-3. 2. 2. ... 0. 0. 0.]
[ 0. -3. 2. ... 0. 0. 0.]
[ 0. 0. -3. ... 0. 0. 0.]
...
[ 0. 0. 0. ... -3. 2. 2.]
[ 0. 0. 0. ... 0. -3. 2.]
[ 0. 0. 0. ... 0. 0. -3.]]
条件②の方のQUBOは以下のような感じです。
[[-4. 6. 4. ... 0. 0. 0.]
[ 0. -4. 6. ... 0. 0. 0.]
[ 0. 0. -4. ... 0. 0. 0.]
...
[ 0. 0. 0. ... -4. 2. 0.]
[ 0. 0. 0. ... 0. -4. 2.]
[ 0. 0. 0. ... 0. 0. -4.]]
さらに、条件①と条件②のバランスを考えて足し合わせたものを、QUBOにします。量子ビット数は、配置の総数と同じで429個ですので、QUBOマトリクスのサイズは429×429でした。
シミュレータで解いてみる
今回はオープンソースのシミュレータblueqatと、D-waveのqbsolvで解いてみました。
3個のタイルの時と違って、一発では良い解が得られないので、何回もループして良い解を探します。
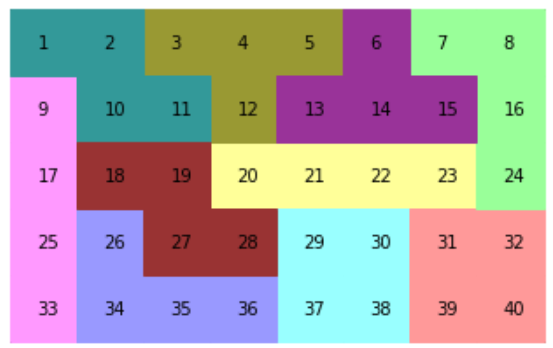
良い解では、例として以下のような結果が得られました!
[13, 33, 66, 68, 144, 223, 251, 298, 339, 352]
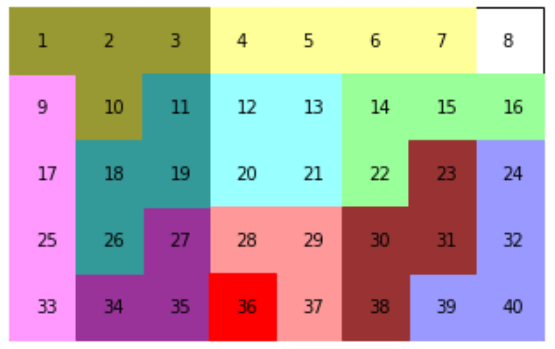
下図のような外れの解も結構でてきます。赤い部分は重なってしまったところです。
まとめ
テトロミノは何とか解けました。次はペントミノ(5つの正方形)に挑戦してみたいと思います!
実はペントミノもコードは書いてみたのですが、量子ビット数が多くて、工夫しないと解けないようです。解は得られますが、3か所位重なってしまう解がほとんどで、最良でも1か所間違いまでしか得られていません。対称性や、ダメな置き方を省いたりして量子ビット削減しても1870になってしまい、難しいです。他の方法を含め、考えてみます!