はじめに
少し前に、とある東工大の先生から、「ペントミノってアニーリングマシンで解けるのかな?」と聞かれて「やってみます!」と答えてしまいましたので、なんとか解いてみたいと思いました。
ペントミノとは(https://ja.wikipedia.org/wiki/%E3%83%9A%E3%83%B3%E3%83%88%E3%83%9F%E3%83%8E
ただし、ペントミノは5個の正方形を組み合わせたピースが12個あり、数が多くて大変なので、まずは問題を小さくして、3×3のタイルを敷き詰める問題を考えてみます。
問題
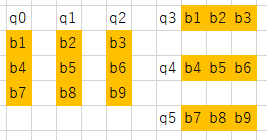
下図左のような正方形3つでできたタイル3つを、下図右のような3×3の盤面にピッタリ敷き詰める問題を考えてみます。
左からピースをp1, p2, p3とします。本物のペントミノでは、同じ形のピースはないのですが、3×3への敷き詰めを考えてここでは許容します。

考え方
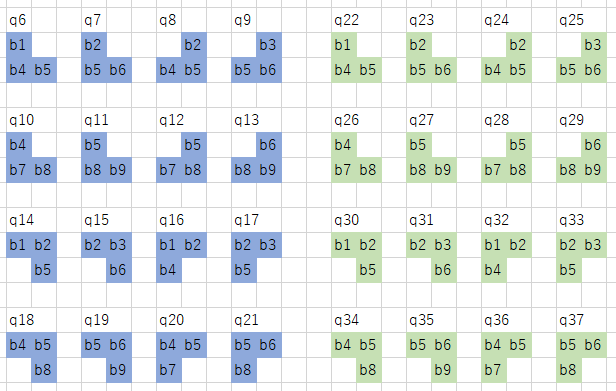
まずは、ピースp1の盤面への置き方を考えてみます。下図のように6通りあります。この置き方を、それぞれ「q0, q1, q2, q3, q4, q5」とします。
立式
次に、アニーリングマシンで解けるように立式してみます。
量子ビットが表すものを決める
ピースp1は、q0~q5のどれかの置き方になるはずですので、置き方q0になるときに、q0=1 、q0にならない時 q0=0 とします。
同様にして、q1になるとき、q1=1, ならないときq1=0・・・、ピースp2についても、置き方q6になるときq6=1, ならないときq6=0・・・とします。
各ピースについて、置き方の中から1つだけ選ばれるようにする
まずは、p1の置き方は「q0, q1, q2, q3, q4, q5」の6個がありますが、その中から1つだけがえらばれなければなりません。
そのため、この6個の量子ビットの中から1つだけが選ばれる、という条件を最小値問題の式にしてみます。以下のようになります。
\{1-(q0+q1+q2+q3+q4+q5)\}^2
これで、q0~q5の中で、1のとき最小値の0、それ以外は1以上の値になります。
同様にして、ピースp2, p3についても立式すると
\{1-(q6+q7+q8+q9+q10+q11+q12+q13+q14+q15+q16+q17+q18+q19+q20+q21)\}^2
\{1-(q22+q23+q24+q25+q26+q27+q28+q29+q30+q31+q32+q33+q34+q35+q36+q37)\}^2
盤面の各位置(b1, b2, b3・・・)に置くピースが重ならないようにする
次に、盤面に注目します。
盤面の「b1」の位置に置かれる可能性のあるピースの配置は、図から「q0,q3,q6,q14,q16,q22,q30,q32」であることが分かります。ピースは重なってもだめだし、どれか1つは配置されていないとダメなので、b1上に来る可能性のあるピースの中から、1つだけを選ぶ必要があります。先ほどと同様に立式すると、
\{1-(q0+q3+q6+q14+q16+q22+q30+q32)\}^2
とすれれば、盤面の位置b1に置かれるピースの配置が1つのみに絞られます。
盤面の位置b2, b3, b4, b5・・・についても同様に立式します。
式全体
ちょっと面倒ですが、全部のピース・盤面の位置についての条件を列挙して足し合わせると、以下の式になります。
\{1-(q0+q1+q2+q3+q4+q5)\}^2 \\
+\{1-(q6+q7+q8+q9+q10+q11+q12+q13+q14+q15+q16+q17+q18+q19+q20+q21)\}^2 \\
+\{1-(q22+q23+q24+q25+q26+q27+q28+q29+q30+q31+q32+q33+q34+q35+q36+q37)\}^2 \\
+\{1-(q0+q3+q6+q14+q16+q22+q30+q32)\}^2 \\
+\{1-(q1+q3+q7+q8+q14+q15+q16+q17+q23+q24+q30+q31+q32+q33)\}^2 \\
+\{1-(q2+q3+q9+q15+q17+q25+q31+q33)\}^2 \\
+\{1-(q0+q4+q6+q8+q10+q16+q18+q20+q22+q24+q26+q32+q34+q36)\}^2 \\
+\{1-(q1+q4+q6+q7+q8+q9+q11+q12+q14+q17+q18+q19+q20+q21+q22+q23+q24+q25+q27+q28+q30+q33+q34+q35+q36+q37)\}^2 \\
+\{1-(q2+q4+q7+q9+q13+q15+q19+q21+q23+q25+q29+q31+q35+q37)\}^2 \\
+\{1-(q0+q5+q10+q12+q20+q26+q28+q36)\}^2 \\
+\{1-(q1+q5+q10+q11+q12+q13+q18+q21+q26+q27+q28+q29+q34+q37)\}^2 \\
+\{1-(q2+q5+q11+q13+q19+q27+q29+q35)\}^2
シミュレータblueqatで解いてみる
式はできたので、シミュレータblueqatで解いてみます。コードは以下の通り。
a = opt.opt()
a = opt.opt()
a.qubo = opt.optm("(1-(q0+q1+q2+q3+q4+q5))^2 \
+(1-(q6+q7+q8+q9+q10+q11+q12+q13+q14+q15+q16+q17+q18+q19+q20+q21))^2 \
+(1-(q22+q23+q24+q25+q26+q27+q28+q29+q30+q31+q32+q33+q34+q35+q36+q37))^2 \
+(1-(q0+q3+q6+q14+q16+q22+q30+q32))^2 \
+(1-(q1+q3+q7+q8+q14+q15+q16+q17+q23+q24+q30+q31+q32+q33))^2 \
+(1-(q2+q3+q9+q15+q17+q25+q31+q33))^2 \
+(1-(q0+q4+q6+q8+q10+q16+q18+q20+q22+q24+q26+q32+q34+q36))^2 \
+(1-(q1+q4+q6+q7+q8+q9+q11+q12+q14+q17+q18+q19+q20+q21+q22+q23+q24+q25+q27+q28+q30+q33+q34+q35+q36+q37))^2 \
+(1-(q2+q4+q7+q9+q13+q15+q19+q21+q23+q25+q29+q31+q35+q37))^2 \
+(1-(q0+q5+q10+q12+q20+q26+q28+q36))^2 \
+(1-(q1+q5+q10+q11+q12+q13+q18+q21+q26+q27+q28+q29+q34+q37))^2 \
+(1-(q2+q5+q11+q13+q19+q27+q29+q35))^2 "
,38)
res = a.sa()
print(res)
print(np.where(np.array(res)==1)[0])
結果
以下のような結果が得られました
[0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[ 5 6 31]
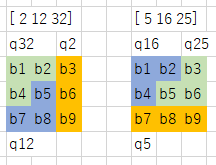
q5, q6, q31が選ばれていますので、組み合わせてみると・・・

このように、ちゃんと敷き詰めできています!
何回か実行すると、下図のようないくつかの結果が得られました。いずれも敷き詰めができました。
まとめ
3×3のタイルの敷き詰めはできました。
ペントミノの場合、ピースも12に増え、さらに「裏返す」と形が異なるピースもあることから置き方が一気に増えますが、「1つのピースの置き方」については古典で十分洗い出し可能だと思いますので、古典のプログラミングで立式はできそうです。量子ビット数が多くなるので、イジングで解けるかどうか分かりませんが、やってみたいと思います。
利用したシミュレータblueqatは以下から利用できます。
https://github.com/Blueqat/Blueqat