はじめに
量子コンピュータで解くのに面白いパズルは無いかなぁと探していて、EternityIIという敷き詰めパズルを見つけました。2007年に発売され、解けたら$2 million prize(約2億円以上?)の懸賞金付きだったそうです。wikipedia によれば、結局誰も解けずに懸賞金の期限が来たそうで、いまだに解けていないようです。

https://en.wikipedia.org/wiki/Eternity_II_puzzle
組み合わせの問題なので、量子コンピュータに向いていそうです!
いきなり大きなのを解くのは難しいので、まずは小さい問題を作って、モデルを考えてみます。
パズルの内容
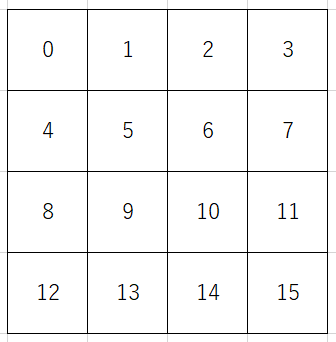
今回は、以下のような4×4=16ピースの敷き詰めパズルを考えます。1つのピースは、対角線で4つの部分に分かれており、それぞれの場所が色で塗られています。敷き詰めたときに、上下・左右の部分の色が同じになるように並べます。テキトウに塗り分けてしまうと正解がないパズルになってしまうので、下図のように正解が必ずあるパターンを作り、切り取って、バラバラにした状態から始めます。

方針
1つのピースをボードに置く置き方はいろいろな置き方があります。置く場所もそうですし、回転も4方向あります。1つ1つのピースについて、可能な置き方をすべて列挙します。そして、その置き方をすべて重ね合わせ、その中から最適な組み合わせを選ぶ、という方針で進めます。
ボードとピースの表現
ピースは、グレー:0、黄:1、紫:2、ピンク:3、緑:4、青:5、オレンジ:6とします。 回転があるので、左・上・右・下の順に色を並べた配置を、例えば[1,2,3,4]のように表します。
このようにして、16個すべてのピースを表すと、以下のようになります。
p = [[0,0,1,2],[0,0,3,6],[0,0,5,4],[0,0,6,3],
[0,4,3,1],[0,6,1,4],[0,4,2,6],[0,3,5,2],
[0,2,1,5],[0,6,5,3],[0,2,5,4],[0,4,1,6],
[2,6,5,3],[1,5,3,2],[4,3,2,1],[5,1,6,4]]
ピースのボードへの置き方を列挙する
次に、ピースの回転とボードのどこに置くかを考え、すべての可能性を列挙します。先ほどのピースの表現に、最初にボードのどこに置くかを追加し、[12,1,2,3,4]のように表します。例えば、これは12の場所に、左:黄色、上:紫、右:ピンク、下:緑になるように置く、という意味です。
パズルの特性上、角のピースと辺のピース、それ以外のピースに分けられるので、それらに分けて考えます。
最初の角
対称性を考えて、最初の1つの角については、置き方を固定してしまいます。グレーが2つある[0,0,1,2]のピースを、左上の角に置く、ということに固定してしまいます。置き方の列挙をprbという配列で表し、prb[ピースの種類][置き方]という構造にして、最初のピースの置き方を以下のように追加します。
prb = [[[0, 0, 0, 1, 2]]]
他の3つの角
他の3つの角には、0が2つある他の3つのピースをそれぞれの場所に置くことができるので、各ピースにつき3通りあります。すべてを配列prbに追加します。追加後のprbは以下のようになります。
prb = [[[0, 0, 0, 1, 2]], [[12, 0, 3, 6, 0], [15, 3, 6, 0, 0], [3, 6, 0, 0, 3]], [[12, 0, 5, 4, 0], [15, 5, 4, 0, 0], [3, 4, 0, 0, 5]], [[12, 0, 6, 3, 0], [15, 6, 3, 0, 0], [3, 3, 0, 0, 6]]]
辺に並べるピース
辺における場所は全部で8か所あるので、各ピースにつき8通りの置き方があります。それらをすべて列挙します。
(長いので配列は書きません。。。)
中央4つに置かれるピース
中央の4つに置かれるピースについても、その置き方をすべて列挙します。4つのピースを、4か所に、4回転の置き方があるので、1つのピースにつき、置く場所が4通り、回転が4通りなので16通りあります。
(これも長いので配列は書きません。。。)
立式
次に、これを量子コンピュータ(イジングモデル)で解けるように立式します。
イジングモデルでは、変数(量子ビット)の取れる値が0か1で、最小値問題として定式化します。
量子ビットが表すものを決める
上で列挙した、「ピースのボードへの置き方」を量子ビットで表します。あるピースをある置き方にする場合は1、しない場合は0、のように考えます。すべてのピースの置き方は、
$$
1+3\times 3+8\times 8+4\times 4 \times 4
$$
ありましたので、使う量子ビット数は138ビットになりました。
この138のビットから、適切な組み合わせを抽出する最小化問題の式を作ります。
1.1つのピースは1度しか使えない
まず、1つのピースは1度しか使わないので、それを最小化問題に立式します。例えば、2つ目のピースの置き方を表す量子ビットは「q1, q2, q3」の3つがありますが、そのうち1つだけが1の時最小になる式は
{\{1-(q1+q2+q3)\}^2}
のようになります。このようにして、16個のピースについてすべて立式し、それらを足し合わせます。
2.ボートの1つのセルには1つのピースしか置けない
ボードにピースを重ねておくことはできないので、同じ場所に置かれる組み合わせは、その中から1つ選ぶ必要があります。例えば、右上の角に置くことができる置き方を表す量子ビットは「q3, q6, q9」なので、このうち1つだけが1の時最小になる式は
{\{1-(q3+q6+q9)\}^2}
のようになります。ボードのすべてのセルについてこれを立式し、足し合わせます。
3.上下・左右の隣り合わせの色が同じになるような制約条件
上下・左右に置かれる可能性のあるピースの組み合わせについて、同じ色なの時に最小になるように立式します。例えば、$q_n$と$q_m (n \neq m)$が隣り合う場合、隣り合った部分が同じ色の場合、$-q_nq_m$、異なる場合$+q_nq_m$という式を追加していきます。こうすることで、違う色が隣り合ってしまったときに高く、同じ色の場合低い値になります。
最後に、作成した3つの式をすべて足し合わせます。
QUBO作成
イジングモデルやQAOAで解けるようにQUBOマトリクスの形にします。式1のマトリクスは以下のような感じです。Qやり方はここでは省略します。。。
このようにして、それぞれ式1、式2、式3のQUBOマトリクスを作り、それぞれqubo1, qubo2, qubo3とします。
[[-1. 0. 0. ... 0. 0. 0.]
[ 0. -1. 2. ... 0. 0. 0.]
[ 0. 0. -1. ... 0. 0. 0.]
...
[ 0. 0. 0. ... -1. 2. 2.]
[ 0. 0. 0. ... 0. -1. 2.]
[ 0. 0. 0. ... 0. 0. -1.]]
シミュレータqbsolvで解きます。
qbsolvは、D-wave社が作成したQUBOシミュレータです。上で作成したquboをqbsolv用に変換して、以下のようにして問題を解きます。
import dimod
from dwave_qbsolv import QBSolv
bqm = dimod.BinaryQuadraticModel.from_qubo(Q, offset = 0.0)
response = QBSolv().sample_qubo(Q, solver_limit=200, num_repeats=100, verbosity=0, algorithm=0)
answers = list(response.samples())
print(response)
結果として、以下のような解が得られました。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ... 137 energy num_oc.
0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 1 0 ... 0 -44.0 74
1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 1 0 ... 0 -42.0 1
2 1 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 ... 0 -41.0 14
3 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 ... 0 -41.0 1
4 1 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 ... 0 -40.0 5
5 1 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 ... 0 -40.0 6
6 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 ... 0 -40.0 3
7 1 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 ... 0 -40.0 1
8 1 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 ... 0 -40.0 2
9 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 ... 0 -40.0 3
10 1 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 ... 0 -38.0 1
['BINARY', 11 rows, 111 samples, 138 variables]
一番エネルギーが低い解が、「1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 1 0 ...」のようになっていますが、ここで「1」になっている量子ビットが表すピースの置き方が、正しい置き方という意味です。
これをプロットしてみると。。。
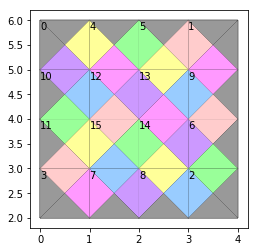
このようにして、正解を得ることができました!
何度やっても同じ解が出るので、このパターンでは解は1つのようです。
まとめ
量子コンピュータ(イジングモデル)のシミュレータを使って、Eternity IIを小さくした問題を使ってモデルを作ることができました。実機は使っていませんが、138ビットですと分割しないと解けなさそうです。
実際のEternity IIは、16×16=256ピースあるので、量子ビット数を概算すると20万ビット位になってしまいそうです!そうなると、このやり方ではなかなか難しそう。でも解けたら楽しいですね!