Shearとは
Shear(せん断・剪断・シアー・スキュー・skew)とはアフィン変換の一種で、下の様にある軸にそって引き伸ばす変換です。

しかし残念ながら、UnityにはShearを行う機能はありません。
ただ実は回転とスケールの合成だけでShear変換を作ることができるので、代わりにこれで実装します。
Shear変換行列の分解
実装の前に行列ではどのように表現されるのかみてみましょう。
Shearは次の変換行列で表される変換です。
\begin{pmatrix}
1 & x \\
0 & 1 \\
\end{pmatrix}
唐突ですが、$x$を次のように表します。
x = \frac{1}{\tan \theta}
すると、Shearは次のように回転行列と対角行列の積に分解できることが知られています。
(この導出は調べた限り分かりませんでした…ご存知の方は教えてください)
\begin{pmatrix}
1 & \frac{1}{\tan\theta} \\
0 & 1 \\
\end{pmatrix} =
\begin{pmatrix}
\frac{\sqrt2}{\sin\theta} & 0 \\
0 & \sqrt2
\end{pmatrix}
\begin{pmatrix}
\cos -45 ^\circ & -\sin -45 ^\circ \\
\sin -45 ^\circ & \cos -45 ^\circ
\end{pmatrix}
\begin{pmatrix}
\sin\frac{\theta}{2} & 0 \\
0 & \cos\frac{\theta}{2}
\end{pmatrix}
\begin{pmatrix}
\cos\frac{\theta}{2} & -\sin\frac{\theta}{2} \\
\sin\frac{\theta}{2} & \cos\frac{\theta}{2}
\end{pmatrix}
これはつまり、単純な回転とスケールだけでShearを行えることを意味しています。
また、
\phi = 90 ^\circ - \theta
とおくことで
\begin{pmatrix}
1 & \tan\phi \\
0 & 1 \\
\end{pmatrix}
=
\begin{pmatrix}
\frac{\sqrt2}{\sin90^\circ - \phi} & 0 \\
0 & \sqrt2
\end{pmatrix}
\begin{pmatrix}
\cos -45 ^\circ & -\sin -45 ^\circ \\
\sin -45 ^\circ & \cos -45 ^\circ
\end{pmatrix}
\begin{pmatrix}
\sin\frac{90^\circ - \phi}{2} & 0 \\
0 & \cos\frac{90^\circ - \phi}{2}
\end{pmatrix}
\begin{pmatrix}
\cos\frac{90^\circ - \phi}{2} & -\sin\frac{90^\circ - \phi}{2} \\
\sin\frac{90^\circ - \phi}{2} & \cos\frac{90^\circ - \phi}{2}
\end{pmatrix}\tag{1}
と表すこともできます。
Unityでの実装
(1)の変換をコードに落とし込んでいきましょう。
次のようなコンポーネントを作ります。
using UnityEngine;
[ExecuteAlways]
public class Shear : MonoBehaviour
{
[Range(-90, 90)] public float phi = 30f;
private void OnValidate()
{
// z軸回りにShearさせる
float angle = 90 - phi;
// 一つのTransformでは、Scale→Rotationの順に適用されることに注意
transform.localRotation = Quaternion.Euler(0, 0, angle / 2);
transform.parent.localScale = new Vector3(Mathf.Sin(angle * Mathf.Deg2Rad / 2), Mathf.Cos(angle * Mathf.Deg2Rad / 2), 1);
transform.parent.localRotation = Quaternion.Euler(0, 0, -45);
transform.parent.parent.localScale = new Vector3(Mathf.Sqrt(2) / Mathf.Sin(angle * Mathf.Deg2Rad), Mathf.Sqrt(2), 1);
}
}
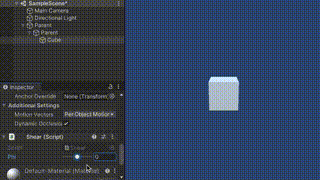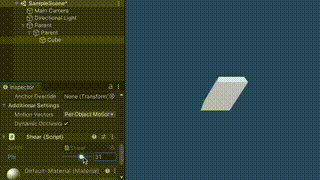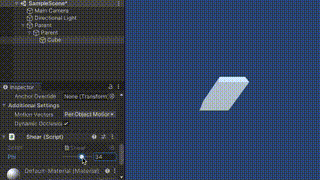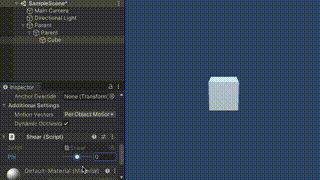
これをShear対象のオブジェクトにアタッチし、親として2つEmptyオブジェクトを設定します。
その状態でスライダーを動かすとShearすることがわかります。
参考
https://www.cs.cmu.edu/~fp/courses/02-graphics/asst2/solution/asst2-sol.pdf
https://answers.unity.com/questions/961330/shear-transformation-using-gameobject-transformati.html
https://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0