解析的7自由度逆運動学とは
逆運動学は目標位置を満たすようにモデルの各関節の回転角を求める問題です。IKとも呼ばれます。
特に7自由度逆運動学は、人間の肩-肘-手首の関節をモデルとした逆運動学です。
一般的に逆運動学は解析解がもとまらない(数値的に計算するしかない)のですが、肩-肘-手首の関節モデルに関しては解析的に解を求めることができます。
百聞は一見にしかずなので、以下のデモをご覧ください。
リンクを押すと操作可能なデモが見れますが、ギズモを動かすと腕が追従することがわかります。
https://arihide.github.io/demos/analytical_ik/
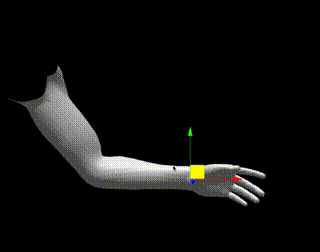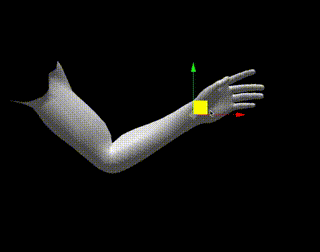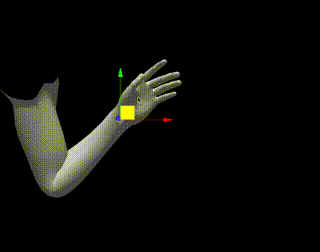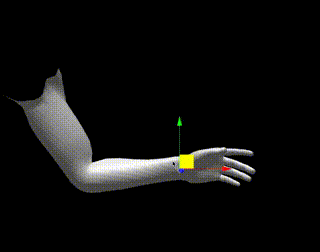
計算方法
モデルの準備
計算に前に適切にモデルのボーンが設定されていることを確認してください。
本記事では以下のように、Tポーズを元の状態とし
腕の方向をy軸、正面下方向をx軸、手前方向をz軸としています。
下をx軸としている理由は、正の方向(右ねじの方向)に肘を回転させたときに自然な方向にするためです。
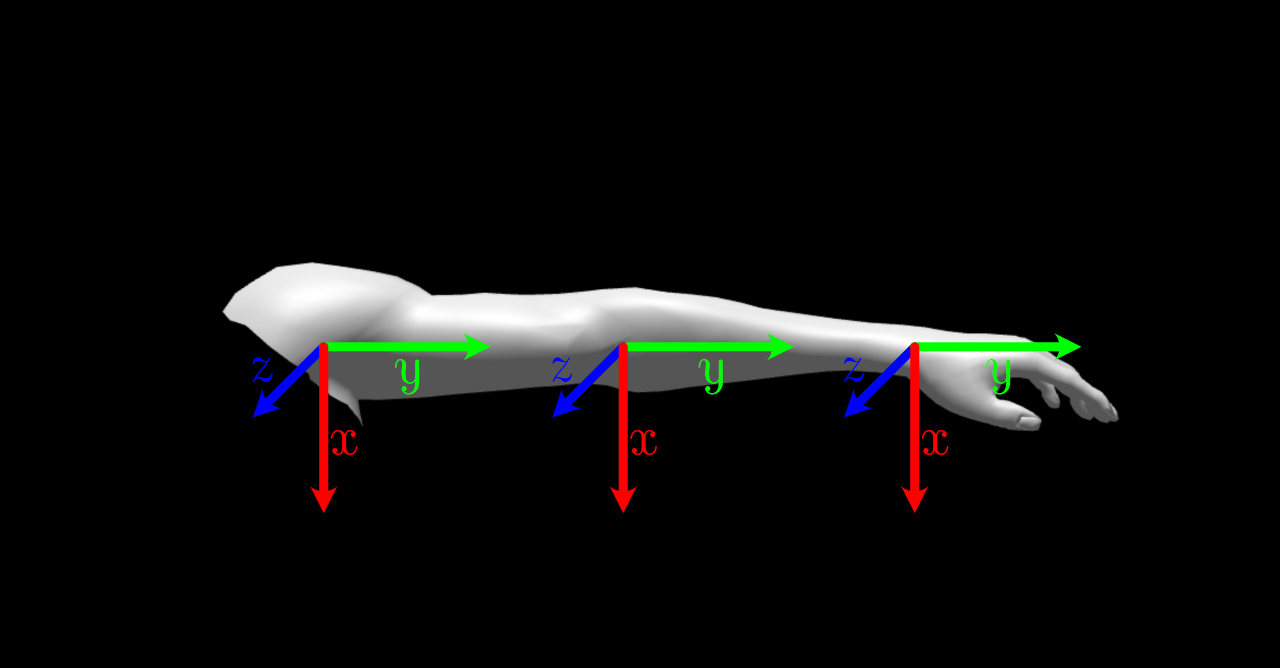
例えば腕の方向がx軸であったりする分には問題ありませんが、そもそも腕の方向と軸が合っていないモデルの場合はIKの計算ができなくなるので注意してください。
IKの定式化
解くべき問題を整理すると以下になります。
手首の目標位置 $\mathbf p$ 目標回転行列 $R$が与えられている。
肩・肘・手首のローカル回転行列 $R_{shoulder}, R_{elbow}, R_{wrist}$ を求めよ。
ただし、
・肩の位置を原点とする。
・上腕(肩から肘まで)の長さを$L_1$ 前腕(肘から手首まで)の長さを$L_2$ とする。
・肘はx軸周りにしか回転することはできない。
解の分布
実際に求める前に、解がどのように存在しているのかを見ましょう。
以下の画像のように、目標手首位置に対する肩・肘の姿勢が決まったとしましょう。
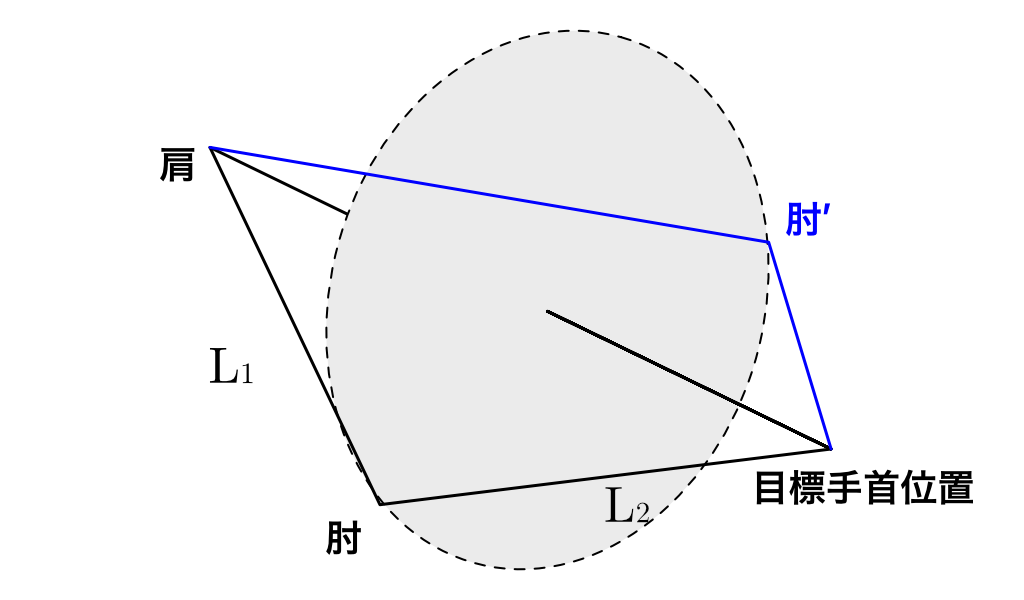
見ればわかる通り、実は肘の位置は肘’に存在していても正しいIKの解なります。
すなわち、肩から手首までの直線へ、肘から垂線をおろした点を中心とした円周上に無限に解が存在することになります。
ただし、そもそも腕の長さよりも目標が遠ければもとまらないので、解の個数は以下になります。
\left\{ \begin{matrix}
\infty& ( L_1 + L_2 \geqq ||\mathbf p|| ) \\
0 & ( L_1 + L_2 < ||\mathbf p||)
\end{matrix} \right.
回転行列の計算
どのように解が存在するかがわかったところで、実際に求めたい回転行列を計算します。
手首の回転行列
手首の回転行列$R_{wrist}$については、すでに$R$が与えられているのでそのまま使用すればよいです。
$$R_{wrist} = R$$
肘の回転行列
肘の回転角は一意であり、余弦定理で求まります。
$$\theta_{elbow} = \cos^{-1} \frac{L_1^2+L_2^2-||\mathbf p||^2}{2 L_1 L_2}$$
したがって肘の回転行列は以下になります。
R_{elbow} = \begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\theta_{elbow} & -\sin\theta_{elbow} \\
0 & \sin\theta_{elbow} & \cos\theta_{elbow}
\end{pmatrix}
肩の回転行列
肩の計算が一番難しいですが、図形的にどのように変化するかを意識すれば理解できると思います。
肩から手首までのベクトルを正規化したものを$\hat{\mathbf e}_y$とします。
\hat{\mathbf e}_y = \frac{\mathbf p}{||\mathbf p||}
次に$\hat{\mathbf e}_y$と直交する任意の単位ベクトルを$\hat{\mathbf e}_z$とします。
(ここの自由に選べる部分が、解が無限に存在する点につながります。)
求めた二つのベクトルの外積を求めます。
$$ {\mathbf e}_x = \hat{\mathbf e}_y \times \hat{\mathbf e}_z $$
肩の回転角を余弦定理で求めます。
\theta_{shoulder} = \cos^{-1} \frac{L_1^2+||\mathbf p||^2 - L_2^2}{2 L_1 ||\mathbf p||}
求めた回転角を用いてベクトルを回転させます。
\begin{matrix}
\mathbf e_y = \hat{\mathbf e}_y \cos\theta_{shoulder} - \hat{\mathbf e}_z \sin\theta_{shoulder} \\
\mathbf e_z = \hat{\mathbf e}_y \sin\theta_{shoulder} + \hat{\mathbf e}_z \cos\theta_{shoulder}
\end{matrix}
この基底ベクトルを並べることで回転行列$R_{shoulder}$が求まります。
$$R_{shoulder} = \left( \mathbf e_x, \mathbf e_y, \mathbf e_z \right)$$
$\hat{\mathbf e}_z$の選び方
$\hat{\mathbf e}_z$は適当に選べますが、できれば最終的な姿勢がイメージしやすい形で指定したいです。
よく使われるのはPole Targetと呼ばれる肘専用の目標位置です。
Pole Targetを$\mathbf b$として、$\hat{\mathbf e}_y$を法線とする平面に射影したものを$\hat{\mathbf e}_z$とします。
上でデモにおいても、[r]キーを押した後のギズモを操作することでPole Targetを移動させることができます。
実際に移動させると可能な限り肘がPole Targetに向かうことがわかります
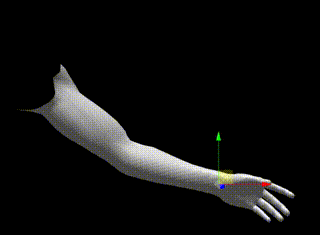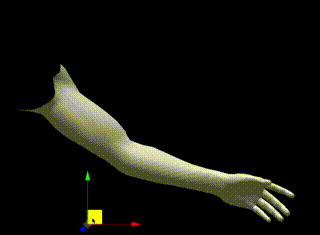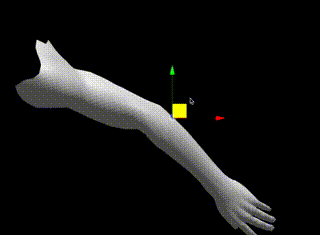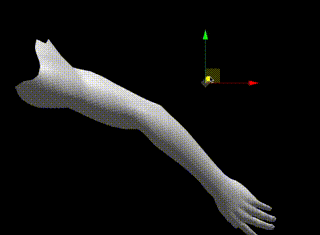
three.jsによる実装
最後に、上で説明した計算を実際に行うソースコードを添付します。
Solve()関数内で解析解を求める処理をしています。
例えば肘の角度の設定方法など、都合上説明と実装が異なってしまう部分がありますが
可能な限りコメントで補足しました。
もし不明な点がありましたらコメントでご連絡ください。
class AnaliticalIK {
constructor(shoulder, elbow, wrist, target, poleTarget, worldInverse) {
this.worldInverse = worldInverse // 肩のボーンの親のワールド逆行列。肩回転時のワールド→ローカルの変換に必要
this.shoulder = shoulder // 肩のボーン。3自由度
this.elbow = elbow // 肘のボーン。1自由度でx軸周りのみ回転
this.wrist = wrist // 手首のボーン。3自由度
this.target = target // 手首の目標位置・回転
this.poleTarget = poleTarget // 肘の目標位置
let shoulderMatrixWorld = shoulder.matrixWorld.elements
let elbowMatrixWorld = elbow.matrixWorld.elements
let wristMatrixWorld = wrist.matrixWorld.elements
this._lowerArmLengthSq =
Math.pow(shoulderMatrixWorld[12] - elbowMatrixWorld[12], 2) +
Math.pow(shoulderMatrixWorld[13] - elbowMatrixWorld[13], 2) +
Math.pow(shoulderMatrixWorld[14] - elbowMatrixWorld[14], 2)
this._foreArmLengthSq =
Math.pow(wristMatrixWorld[12] - elbowMatrixWorld[12], 2) +
Math.pow(wristMatrixWorld[13] - elbowMatrixWorld[13], 2) +
Math.pow(wristMatrixWorld[14] - elbowMatrixWorld[14], 2)
this._lowerArmLength = Math.sqrt(this._lowerArmLengthSq) // 上腕(肩から肘まで)の長さ
this._foreArmLength = Math.sqrt(this._foreArmLengthSq) // 前腕(肘から手首までの)長さ
}
solve() { // 実際に逆運動学で関節角度を求める処理
let shoulderToWrist = new THREE.Vector3(
this.target.position.x - this.shoulder.matrixWorld.elements[12],
this.target.position.y - this.shoulder.matrixWorld.elements[13],
this.target.position.z - this.shoulder.matrixWorld.elements[14]
)
let lowerArmLength = this._lowerArmLength; // 上腕(肩から肘まで)の長さ
let lowerArmLengthSq = this._lowerArmLengthSq
let foreArmLength = this._foreArmLength; // 前腕(肘から手首までの)長さ
let foreArmLengthSq = this._foreArmLengthSq
let shoulderToWristLengthSq = shoulderToWrist.lengthSq()
let shoulderToWristLength = Math.sqrt(shoulderToWristLengthSq) // 肩から目標手首位置までの長さ
// 目標位置が腕の長さより遠い時、解は存在しないので丸める
if (shoulderToWristLength > lowerArmLength + foreArmLength) {
shoulderToWristLength = lowerArmLength + foreArmLength
shoulderToWristLengthSq = shoulderToWristLength * shoulderToWristLength
}
// 肘の回転角を余弦定理で求める
let elbowAngle = Math.acos((lowerArmLengthSq + foreArmLengthSq - shoulderToWristLengthSq) / (2 * lowerArmLength * foreArmLength));
// モデルはT-Poseなので肘を開き切った時が0°、曲げ切った時が180°である。なので外角を回転角として設定する。
this.elbow.rotation.set(Math.PI - elbowAngle, 0, 0)
// 肩の回転を求めるために基底ベクトルを求める
let targetDir = shoulderToWrist.normalize()
let poleDir = new THREE.Vector3(
this.poleTarget.position.x - this.shoulder.matrixWorld.elements[12],
this.poleTarget.position.y - this.shoulder.matrixWorld.elements[13],
this.poleTarget.position.z - this.shoulder.matrixWorld.elements[14]
).projectOnPlane(targetDir).normalize().negate() // z軸は肘の曲がる方向と逆を正にとっているので反転させる
let other = targetDir.clone().cross(poleDir)
let cos = (shoulderToWristLengthSq + lowerArmLengthSq - foreArmLengthSq) / (2 * shoulderToWristLength * lowerArmLength)
let sin = Math.sqrt(1 - cos * cos)
// 基底ベクトルから肩の回転行列を作成
let shoulderRotationMatrix = new THREE.Matrix4().set(
other.x, targetDir.x * cos - poleDir.x * sin, targetDir.x * sin + poleDir.x * cos, 0,
other.y, targetDir.y * cos - poleDir.y * sin, targetDir.y * sin + poleDir.y * cos, 0,
other.z, targetDir.z * cos - poleDir.z * sin, targetDir.z * sin + poleDir.z * cos, 0,
0, 0, 0, 1
)
// 求めた行列はワールド回転行列なのでローカルに変換する
shoulderRotationMatrix.premultiply(this.worldInverse)
// 行列だと並行移動成分等も含まれていてややこしいので、クォータニオンとして設定する
this.shoulder.quaternion.setFromRotationMatrix(shoulderRotationMatrix)
// 手首の回転を設定
this.wrist.quaternion.copy(this.target.quaternion)
}
}
ソースコード全文はこちらをご覧ください。
参考
Tolani et al. Real-time inverse kinematics techniques for anthropomorphic limbs
https://www.cis.upenn.edu/~badler/gmod/0528a.pdf
7自由度解析的IK
https://mukai-lab.org/content/AnalyticalInverseKinematics.pdf